5.1.2.1垂线 课件(共29张PPT)2022-2023学年人教版七年级数学下册
文档属性
| 名称 | 5.1.2.1垂线 课件(共29张PPT)2022-2023学年人教版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 691.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-05 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
5.1.2 垂线
七年级数学(上册) 人教版
七年级数学组
主 备 人:
议课组长:
议课日期:2023.2.2
授课日期:
第五章 相交线和平行线
1.会用符号表示两直线垂直,理解垂线的概念,会用三角尺或量角器过一点画已知直线的垂线。
学习目标(1分钟)
2.探究归纳并掌握垂线的性质,会利用所学知识进行简单
的推理。
中考考点:画垂线段,垂线定义与性质,点到直线的距离
3.理解点到直线的距离
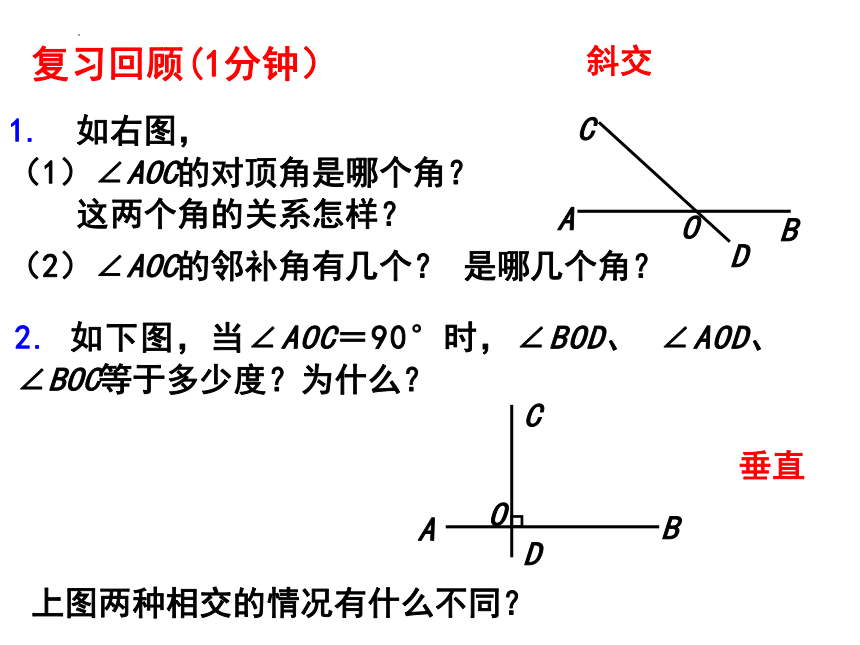
1. 如右图,
(1)∠AOC的对顶角是哪个角?
这两个角的关系怎样?
(2)∠AOC的邻补角有几个? 是哪几个角?
2. 如下图,当∠AOC=90°时,∠BOD、 ∠AOD、∠BOC等于多少度?为什么?
A
C
B
D
O
A
B
C
D
O
复习回顾(1分钟)
上图两种相交的情况有什么不同?
斜交
垂直
自学指导1(2分钟)
仔细阅读课本P3-4,思考下列问题:
学生自学,教师巡视(4分钟)
两条相交直线在什么情况下是垂直的?什么叫垂线?什么叫垂足?
如何表示垂直?
2.垂直该如何书写?
自学指导1(2分钟)
仔细阅读课本P3-4,思考下列问题:
学生自学,教师巡视(4分钟)
两条相交直线在什么情况下是垂直的?什么叫垂线?什么叫垂足?
(2)垂直的符号是___,如图直线AB与直线CD垂直,记作
________________,直线m与直线n垂直,记作_____
(1)两条直线相交所成的四个角中任意一个角是 ,
那么这两条直线 ,其中一条直线叫做另一
条直线的_____,它们的交点叫做_____.
直角
垂线
垂足
互相垂直
⊥
AB⊥CD,垂足为O
m⊥n
用“⊥”和直线字母表示垂直
AB⊥CD于O
如何表示垂直?
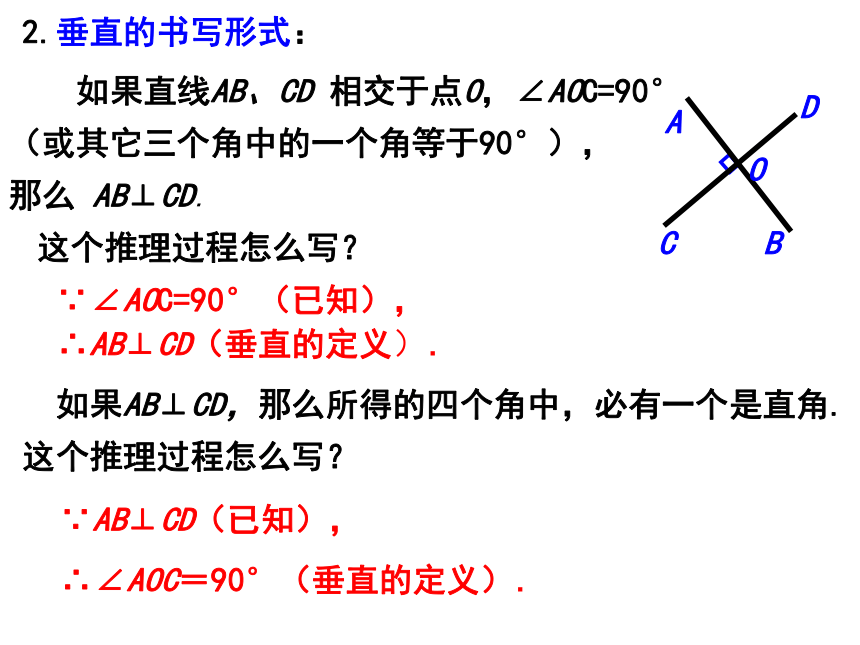
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°
(或其它三个角中的一个角等于90°),
那么 AB⊥CD.
这个推理过程怎么写?
∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角. 这个推理过程怎么写?
A
B
C
D
O
2.垂直的书写形式:
F
E
M
N
O
记作:MN⊥EF ,垂足为O.
或者MN⊥EF于O
A
B
O
E
记作:AB⊥OE垂足为O.
或者AB⊥OE于O
自学检测1(1分钟)
1.如何用几何语言表示?
自学指导2(1分钟)
仔细阅读教材P4,思考下列问题:
学生自学,教师巡视(5分钟)
2.如何画已知直线的垂线
3.讨论
(1)画已知直线l的垂线能画几条
(2)过直线l上的一点A画l的垂线,这样的垂线能画几条
(3)过直线l外的一点B画l的垂线,这样的垂线能画几条
A
.B
l
.
1.垂线是一条直线还是线段,还是射线
如遇到线段与线段、线段与射线、射线与射线、线段或射线与直线垂直,特指它们所在的直线互相垂直。
过已知点画已知直线的垂线,实际上就是过已知点画一条直线,使所画直线与已知直线相交所成的角是90°.
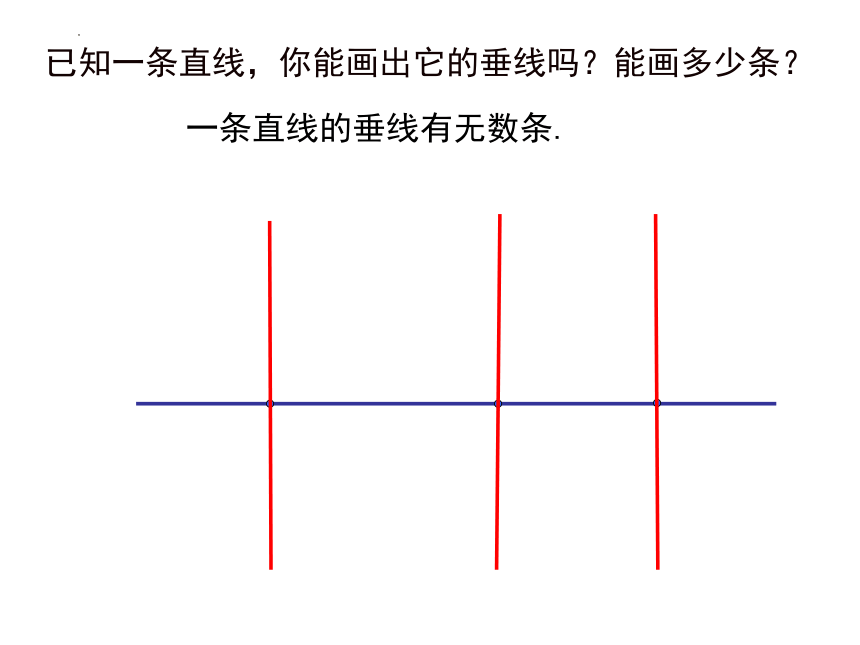
一条直线的垂线有无数条.
已知一条直线,你能画出它的垂线吗?能画多少条?
o
1. 放
2. 靠
3. 移
4. 画
过直线上一点有且只有一条直线与已知直线垂直.
过直线上一点能画这条直线的垂线吗?能画几条?
如图,已知直线 l 和l上的一点A ,作l的垂线.
A
1. 放
2. 靠
3. 移
4. 画
过直线外一点有且只有一条直线与已知直线垂直.
过直线外一点能画这条直线的垂线吗?能画几条?
如图,已知直线 l 和l外的一点A ,作l的垂线.
l
讨论、更正、点拨(3分钟)
1.过点A作l 的垂线,你能做出多少条?你得到垂线的什么性质?
同一平面内,过一点有且只有一条直线与已知直线垂直
A
A
注意:
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指唯一性.
垂线的性质
E
E
E
解题关键
1.找出线段AB所在直线
2.过点P
3.垂直
4.垂线画成直线
自学检测2(5分钟)
2.过点P向线段AB所在直线引垂线,正确的是( )
A B C D
C
例 如图AB⊥CD垂足为O,∠COF=56°,求∠AOE
解:∵AB⊥CD(已知),
∴∠COB=90°(垂直的定义).
∴∠BOF= ∠COB-∠COF
=90°-56°=34° .
∴ ∠AOE=∠BOF=34°(对顶角相等)
F
E
D
C
B
A
O
56°
1.如何利用垂直的定义求角的度数
自学指导3(1分钟)
学生自学,教师巡视(3分钟)
自学检测3(6分钟)
3.如图,已知AO⊥BC于O,
∠AOD=30°,那么∠DOC= °
1.如图,EO⊥AB于点O,∠EOC=40°
则∠AOD=( )
A.30° B.40° C.50° D.60°
4.如图,OA⊥OB,∠AOC=120°,
则∠BOC等于 度.
2.已知OA⊥OC,过点O作射线OB,且∠AOB=30°
则∠BOC的度数为 .
变式已知OA⊥OC,∠AOB:∠AOC=2:3,
则∠BOC的度数为( )
A.30° B.60° C.150° D.30°或150°
C
D
120 或60
60
30
5.如图,直线AB、CD相交于点O,OE⊥AB, ∠1=55°,求∠EOD的度数.
∴ ∠EOB=90° (垂直的定义).
∴ ∠EOD =∠EOB +∠BOD =90°+55°=145°.
A
C
E
B
D
O
1
(
∵ AB⊥OE (已知),
∵ ∠BOD =∠1=55° (对顶角相等),
解:
自学检测3(5分钟)
如何利用垂直的定义判定两直线垂直的位置关系
自学指导4(1分钟)
例1 如图,CO⊥AB于点O,∠AOE=∠COF,则射线OE,OF是什么位置关系?请说明理由.
解:射线OE,OF互相垂直.理由如下:
∵CO⊥AB,
∴∠AOC=90°.
又∵∠AOE=∠COF,
∴∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
∴OE与OF互相垂直(垂直定义).
学生自学,教师巡视(3分钟)
自学检测4(4分钟)
1.如图,直线AB,CD相交于点O,过O点画射线OE,OF,使OE⊥CD,OD平分∠BOF.如果∠BOE=50°,求∠AOC,∠EOF和∠AOF的度数.
解:∵OE⊥CD,
∴∠DOE=90°(垂直定义).
∵∠BOE=50°,
∴∠AOC=∠BOD=∠DOE-∠BOE=90°-50°=40°.
∵OD平分∠BOF,
∴∠BOF=2∠BOD=80°.
∴∠EOF=∠BOF+∠BOE=80°+50°=130°,
∠AOF=∠AOB-∠BOF=180°-80°=100°.
如何判断两直线(线段、射线所在直线)互相垂直?
主要依据是垂直定义,只要说明两条相交直线所构成
的四个角中有一个角是直角即可.
点拨(1分钟)
小结(2分钟)
1.垂直的相关定义及表示方法
3.平面内,过一点__________一条直线与已知直线垂直
有且只有
2.垂线的定义及画法
当堂训练(15分钟)
1.如图,点O为直线AB上一点,
OC⊥OD,若∠1=35°,则∠2的度数是( )
A.35° B.45° C.55° D.65°
C
2.如图,已知OA⊥OC,∠BOC=2∠AOB,
则∠AOB的度数等于 .
3.如图,点O是直线AB上一点OC⊥OD,∠AOC:∠BOD=5:1,那么∠AOC的
度数是 .
30°
75°
4.如图,若CD⊥EF,∠1=∠2,则AB⊥EF,请说明理由(补全解题过程).
解:∵CD⊥EF,
∴∠1=_____(垂直的定义).
∴∠2=∠1=___.∴AB__EF(垂直的定义).
90°
90°
⊥
垂线的画法
5.下列选项中,利用三角板过点P画AB的垂线CD,正确的是( )
C
6.过线段外一点,画这条线段的垂线,垂足在( )
A.这条线段上 B.这条线段的端点
C.这条线段的延长线上 D.以上都有可能
D
7.(河南中考)如图,直线AB,CD相交于点O,EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为____________.
140°
8.(教材P8习题T5变式)如图,直线AB,CD相交于点O,OE⊥CD,垂足为O,∠AOC=35°,求∠BOE的度数.
解:∵∠AOC=∠BOD,∠AOC=35°,
∴∠BOD=35°,
∵OE⊥CD,
∴∠EOD=90°,
∴∠BOE=∠EOD-∠BOD=90°-35°=55°
9.(教材P9习题T12变式)已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,那么A,B,C三点在同一条直线上,其理由是______________________________________________
在同一平面内,过一点有且只有一条直线与已知直线垂直
选做题
如图①②所示,将两个相同三角板的两个直
角顶点O重合在一起,像图①②那样放置
(1)若∠BOC=60°,如图①,猜想∠AOD的度数
(2)若∠BOC=70°,如图②,猜想∠AOD的度数
(3)猜想∠AOD和∠BOC的关系,并写出理由
解:(1)∵∠AOB=90°,∠BOC=60°
∴∠AOC=∠AOB﹣∠BOC=90°﹣60°=30°
又∵∠COD=90°
∴∠AOD=∠AOC+∠COD=30°+90°=120°
(2)∵∠AOB+∠COD+∠BOC+∠AOD=360°
∠AOB=90°,∠COD=90°,∠BOC=70°
∴∠AOD=360°﹣∠AOB﹣∠COD﹣∠BOC
=360°﹣90°﹣90°﹣70°
=110°.
解:(3)猜想:∠AOD+∠BOC=180°
理由:
如图①∵∠AOD=∠AOC+∠COD=∠AOC+90°
∠BOC=∠COD﹣∠BOD=90°﹣∠BOD,∠AOC=∠BOD
∴∠AOD+∠BOC=180°.
板书设计
1、垂直的相关定义及表示方法;
2、平面内,过一点有且只有一条直线与已知直线垂直;
5.1.2 垂线
七年级数学(上册) 人教版
七年级数学组
主 备 人:
议课组长:
议课日期:2023.2.2
授课日期:
第五章 相交线和平行线
1.会用符号表示两直线垂直,理解垂线的概念,会用三角尺或量角器过一点画已知直线的垂线。
学习目标(1分钟)
2.探究归纳并掌握垂线的性质,会利用所学知识进行简单
的推理。
中考考点:画垂线段,垂线定义与性质,点到直线的距离
3.理解点到直线的距离
1. 如右图,
(1)∠AOC的对顶角是哪个角?
这两个角的关系怎样?
(2)∠AOC的邻补角有几个? 是哪几个角?
2. 如下图,当∠AOC=90°时,∠BOD、 ∠AOD、∠BOC等于多少度?为什么?
A
C
B
D
O
A
B
C
D
O
复习回顾(1分钟)
上图两种相交的情况有什么不同?
斜交
垂直
自学指导1(2分钟)
仔细阅读课本P3-4,思考下列问题:
学生自学,教师巡视(4分钟)
两条相交直线在什么情况下是垂直的?什么叫垂线?什么叫垂足?
如何表示垂直?
2.垂直该如何书写?
自学指导1(2分钟)
仔细阅读课本P3-4,思考下列问题:
学生自学,教师巡视(4分钟)
两条相交直线在什么情况下是垂直的?什么叫垂线?什么叫垂足?
(2)垂直的符号是___,如图直线AB与直线CD垂直,记作
________________,直线m与直线n垂直,记作_____
(1)两条直线相交所成的四个角中任意一个角是 ,
那么这两条直线 ,其中一条直线叫做另一
条直线的_____,它们的交点叫做_____.
直角
垂线
垂足
互相垂直
⊥
AB⊥CD,垂足为O
m⊥n
用“⊥”和直线字母表示垂直
AB⊥CD于O
如何表示垂直?
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°
(或其它三个角中的一个角等于90°),
那么 AB⊥CD.
这个推理过程怎么写?
∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角. 这个推理过程怎么写?
A
B
C
D
O
2.垂直的书写形式:
F
E
M
N
O
记作:MN⊥EF ,垂足为O.
或者MN⊥EF于O
A
B
O
E
记作:AB⊥OE垂足为O.
或者AB⊥OE于O
自学检测1(1分钟)
1.如何用几何语言表示?
自学指导2(1分钟)
仔细阅读教材P4,思考下列问题:
学生自学,教师巡视(5分钟)
2.如何画已知直线的垂线
3.讨论
(1)画已知直线l的垂线能画几条
(2)过直线l上的一点A画l的垂线,这样的垂线能画几条
(3)过直线l外的一点B画l的垂线,这样的垂线能画几条
A
.B
l
.
1.垂线是一条直线还是线段,还是射线
如遇到线段与线段、线段与射线、射线与射线、线段或射线与直线垂直,特指它们所在的直线互相垂直。
过已知点画已知直线的垂线,实际上就是过已知点画一条直线,使所画直线与已知直线相交所成的角是90°.
一条直线的垂线有无数条.
已知一条直线,你能画出它的垂线吗?能画多少条?
o
1. 放
2. 靠
3. 移
4. 画
过直线上一点有且只有一条直线与已知直线垂直.
过直线上一点能画这条直线的垂线吗?能画几条?
如图,已知直线 l 和l上的一点A ,作l的垂线.
A
1. 放
2. 靠
3. 移
4. 画
过直线外一点有且只有一条直线与已知直线垂直.
过直线外一点能画这条直线的垂线吗?能画几条?
如图,已知直线 l 和l外的一点A ,作l的垂线.
l
讨论、更正、点拨(3分钟)
1.过点A作l 的垂线,你能做出多少条?你得到垂线的什么性质?
同一平面内,过一点有且只有一条直线与已知直线垂直
A
A
注意:
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指唯一性.
垂线的性质
E
E
E
解题关键
1.找出线段AB所在直线
2.过点P
3.垂直
4.垂线画成直线
自学检测2(5分钟)
2.过点P向线段AB所在直线引垂线,正确的是( )
A B C D
C
例 如图AB⊥CD垂足为O,∠COF=56°,求∠AOE
解:∵AB⊥CD(已知),
∴∠COB=90°(垂直的定义).
∴∠BOF= ∠COB-∠COF
=90°-56°=34° .
∴ ∠AOE=∠BOF=34°(对顶角相等)
F
E
D
C
B
A
O
56°
1.如何利用垂直的定义求角的度数
自学指导3(1分钟)
学生自学,教师巡视(3分钟)
自学检测3(6分钟)
3.如图,已知AO⊥BC于O,
∠AOD=30°,那么∠DOC= °
1.如图,EO⊥AB于点O,∠EOC=40°
则∠AOD=( )
A.30° B.40° C.50° D.60°
4.如图,OA⊥OB,∠AOC=120°,
则∠BOC等于 度.
2.已知OA⊥OC,过点O作射线OB,且∠AOB=30°
则∠BOC的度数为 .
变式已知OA⊥OC,∠AOB:∠AOC=2:3,
则∠BOC的度数为( )
A.30° B.60° C.150° D.30°或150°
C
D
120 或60
60
30
5.如图,直线AB、CD相交于点O,OE⊥AB, ∠1=55°,求∠EOD的度数.
∴ ∠EOB=90° (垂直的定义).
∴ ∠EOD =∠EOB +∠BOD =90°+55°=145°.
A
C
E
B
D
O
1
(
∵ AB⊥OE (已知),
∵ ∠BOD =∠1=55° (对顶角相等),
解:
自学检测3(5分钟)
如何利用垂直的定义判定两直线垂直的位置关系
自学指导4(1分钟)
例1 如图,CO⊥AB于点O,∠AOE=∠COF,则射线OE,OF是什么位置关系?请说明理由.
解:射线OE,OF互相垂直.理由如下:
∵CO⊥AB,
∴∠AOC=90°.
又∵∠AOE=∠COF,
∴∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
∴OE与OF互相垂直(垂直定义).
学生自学,教师巡视(3分钟)
自学检测4(4分钟)
1.如图,直线AB,CD相交于点O,过O点画射线OE,OF,使OE⊥CD,OD平分∠BOF.如果∠BOE=50°,求∠AOC,∠EOF和∠AOF的度数.
解:∵OE⊥CD,
∴∠DOE=90°(垂直定义).
∵∠BOE=50°,
∴∠AOC=∠BOD=∠DOE-∠BOE=90°-50°=40°.
∵OD平分∠BOF,
∴∠BOF=2∠BOD=80°.
∴∠EOF=∠BOF+∠BOE=80°+50°=130°,
∠AOF=∠AOB-∠BOF=180°-80°=100°.
如何判断两直线(线段、射线所在直线)互相垂直?
主要依据是垂直定义,只要说明两条相交直线所构成
的四个角中有一个角是直角即可.
点拨(1分钟)
小结(2分钟)
1.垂直的相关定义及表示方法
3.平面内,过一点__________一条直线与已知直线垂直
有且只有
2.垂线的定义及画法
当堂训练(15分钟)
1.如图,点O为直线AB上一点,
OC⊥OD,若∠1=35°,则∠2的度数是( )
A.35° B.45° C.55° D.65°
C
2.如图,已知OA⊥OC,∠BOC=2∠AOB,
则∠AOB的度数等于 .
3.如图,点O是直线AB上一点OC⊥OD,∠AOC:∠BOD=5:1,那么∠AOC的
度数是 .
30°
75°
4.如图,若CD⊥EF,∠1=∠2,则AB⊥EF,请说明理由(补全解题过程).
解:∵CD⊥EF,
∴∠1=_____(垂直的定义).
∴∠2=∠1=___.∴AB__EF(垂直的定义).
90°
90°
⊥
垂线的画法
5.下列选项中,利用三角板过点P画AB的垂线CD,正确的是( )
C
6.过线段外一点,画这条线段的垂线,垂足在( )
A.这条线段上 B.这条线段的端点
C.这条线段的延长线上 D.以上都有可能
D
7.(河南中考)如图,直线AB,CD相交于点O,EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为____________.
140°
8.(教材P8习题T5变式)如图,直线AB,CD相交于点O,OE⊥CD,垂足为O,∠AOC=35°,求∠BOE的度数.
解:∵∠AOC=∠BOD,∠AOC=35°,
∴∠BOD=35°,
∵OE⊥CD,
∴∠EOD=90°,
∴∠BOE=∠EOD-∠BOD=90°-35°=55°
9.(教材P9习题T12变式)已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,那么A,B,C三点在同一条直线上,其理由是______________________________________________
在同一平面内,过一点有且只有一条直线与已知直线垂直
选做题
如图①②所示,将两个相同三角板的两个直
角顶点O重合在一起,像图①②那样放置
(1)若∠BOC=60°,如图①,猜想∠AOD的度数
(2)若∠BOC=70°,如图②,猜想∠AOD的度数
(3)猜想∠AOD和∠BOC的关系,并写出理由
解:(1)∵∠AOB=90°,∠BOC=60°
∴∠AOC=∠AOB﹣∠BOC=90°﹣60°=30°
又∵∠COD=90°
∴∠AOD=∠AOC+∠COD=30°+90°=120°
(2)∵∠AOB+∠COD+∠BOC+∠AOD=360°
∠AOB=90°,∠COD=90°,∠BOC=70°
∴∠AOD=360°﹣∠AOB﹣∠COD﹣∠BOC
=360°﹣90°﹣90°﹣70°
=110°.
解:(3)猜想:∠AOD+∠BOC=180°
理由:
如图①∵∠AOD=∠AOC+∠COD=∠AOC+90°
∠BOC=∠COD﹣∠BOD=90°﹣∠BOD,∠AOC=∠BOD
∴∠AOD+∠BOC=180°.
板书设计
1、垂直的相关定义及表示方法;
2、平面内,过一点有且只有一条直线与已知直线垂直;
