5.1.1 相交线课件(共26张PPT) 2022-2023学年人教版七年级数学下册
文档属性
| 名称 | 5.1.1 相交线课件(共26张PPT) 2022-2023学年人教版七年级数学下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-06 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
第五章 相交线与平行线
5.1.1相交线
人教版 七年级下册
C
D
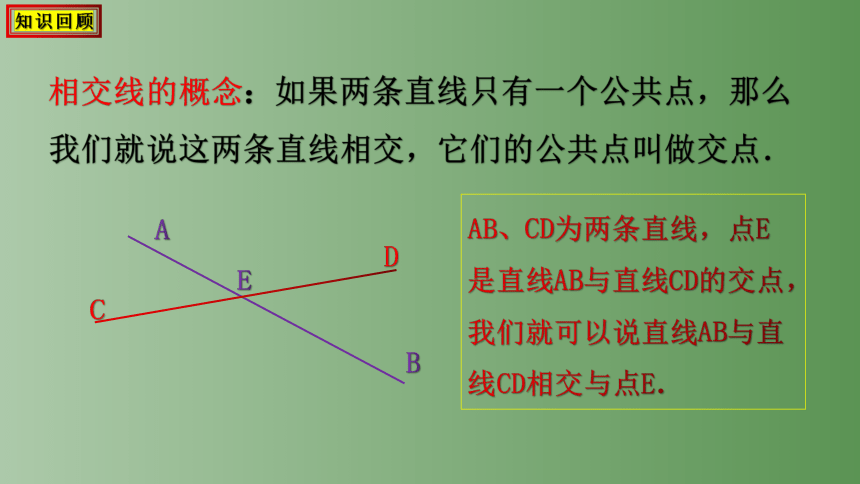
相交线
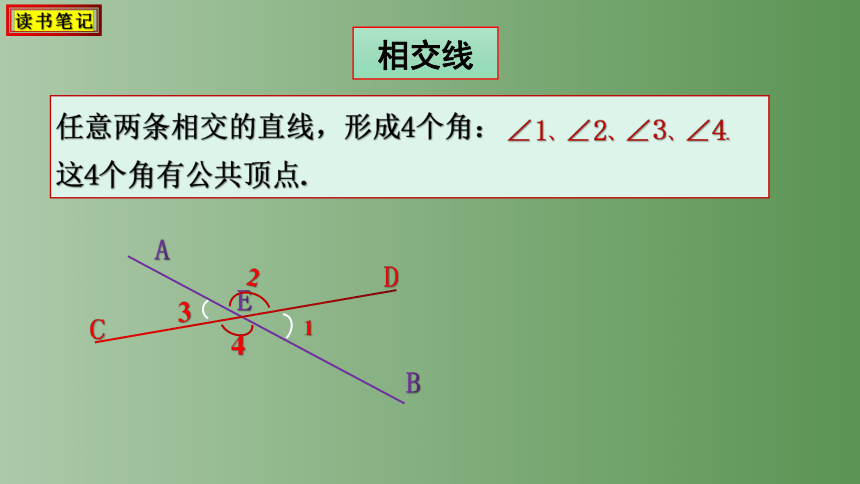
任意两条相交的直线,形成4个角:
这4个角有公共顶点.
C
D
1
2
3
4
∠1、∠2、∠3、∠4.
C
D
1
2
3
4
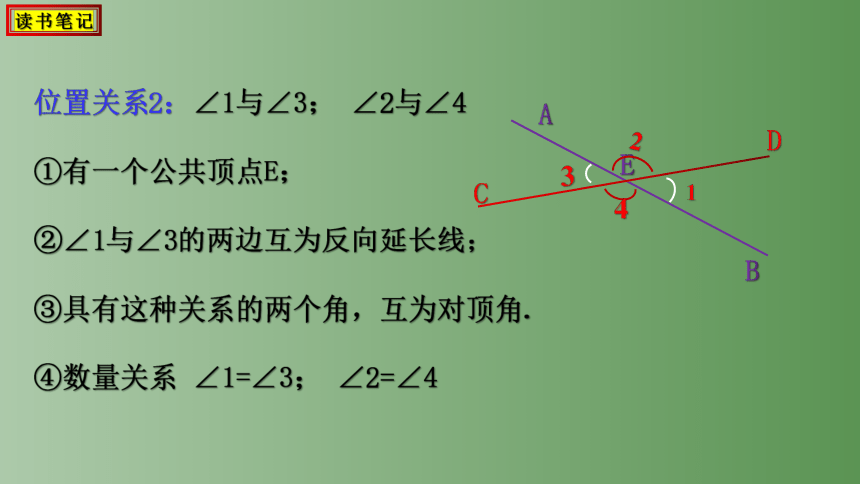
位置关系2:∠1与∠3; ∠2与∠4
①有一个公共顶点E;
②∠1与∠3的两边互为反向延长线;
③具有这种关系的两个角,互为对顶角.
④数量关系 ∠1=∠3; ∠2=∠4
C
D
1
2
3
4
邻补角的性质:邻补角互补
邻补角也可以看成是一条直线与端点在一条直线上的一条射线组成的两个角。
几何语言:
(邻补角互补)
∵∠1与∠2互为邻补角
∴∠1+∠2=180o
几何语言:
对顶角的性质:对顶角相等
∵∠1与∠2互为对顶角 ∴∠1=∠2
(对顶角相等)
(1)∠1的对顶角是( )
A.∠BOC B.∠BOE和∠AOF
C.∠AOE D.∠AOD
A 0 B
1
D
C
F
E
C
(2)∠1的邻补角是( )
A.∠AOF B.∠BOE和∠AOF
C.∠BOC D.∠BOC和∠AOF
B
l2
l1
O
1
2
3
4
∠1的对顶角是______;
∠4的对顶角是______.
∠3
∠2
300
解:由邻补角的定义,得
∠2=180°-∠1=180°-50°=130°;
由对顶角相等,得
∠3=∠1=50°,∠4=∠2=130°.
变式1 如图,直线AB,CD相交于点O,射线OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为 ,
∠BOE的邻补角为 ;
∠BOD
∠AOE
(2)若∠AOC=70°,且∠BOE∶∠EOD=3∶4,
求∠AOE的度数.
解:∵∠BOD=∠AOC=70°,
∵∠BOD=∠BOE+∠EOD,
∵∠BOE∶∠EOD=3∶4,
∴∠BOE=70°÷7×3=300
∴∠AOE=180°-∠BOE=150°.
如图,直线a,b相交,若∠2是∠1的3倍,求∠1,∠2,∠3,∠4的度数.
完成推理过程.如图,直线a,b相交.
证明:∵∠1+∠2 = ,
∠2+∠3 = (邻补角定义)
∴∠1=1800- ,
∠3 =1800- (等式性质)
∴∠1=∠3 (等量代换)
由上面推理可知,对顶角的性质:对顶角 .
定义 图例 性质 几何语言
邻补角 有一条公共边,另一边互为反向延长线的两个角. 邻补角____ ∵∠1与∠2是邻补角∴__________
对顶角 有公共顶点,一角的两边与另一角的两边互为反向延长线. 对顶角_____ ∵∠1与∠3是对顶角∴__________
1.如下图所示,∠1和∠2是对顶角的图形有( ).
A.1个 B.2个 C.3个 D.4个
2.下面∠1和∠2不是邻补角的是( )
3.如图是一把剪刀,若∠AOB+∠COD=82°,则∠BOD= .
4.如图所示,直线AB,CD相交于点O,∠AOC∶∠AOD=2∶3,则∠BOD= °.
5.三条直线AB,CD,EF相交于一点O,
①∠AOD的对顶角是_____,
②∠AOC的邻补角是_______,
③若∠AOC=30°,则∠BOD=______,
∠COB=_______,
∠AOE+∠DOB+∠COF=_____
6.图中是对顶角量角器,用它测量角的原理是 .
7.如图5-1-12,直线AB和CD相交于点O,若∠BOD=40°,OA平分∠EOC,求∠EOD的度数.
第五章 相交线与平行线
5.1.1相交线
人教版 七年级下册
C
D
相交线
任意两条相交的直线,形成4个角:
这4个角有公共顶点.
C
D
1
2
3
4
∠1、∠2、∠3、∠4.
C
D
1
2
3
4
位置关系2:∠1与∠3; ∠2与∠4
①有一个公共顶点E;
②∠1与∠3的两边互为反向延长线;
③具有这种关系的两个角,互为对顶角.
④数量关系 ∠1=∠3; ∠2=∠4
C
D
1
2
3
4
邻补角的性质:邻补角互补
邻补角也可以看成是一条直线与端点在一条直线上的一条射线组成的两个角。
几何语言:
(邻补角互补)
∵∠1与∠2互为邻补角
∴∠1+∠2=180o
几何语言:
对顶角的性质:对顶角相等
∵∠1与∠2互为对顶角 ∴∠1=∠2
(对顶角相等)
(1)∠1的对顶角是( )
A.∠BOC B.∠BOE和∠AOF
C.∠AOE D.∠AOD
A 0 B
1
D
C
F
E
C
(2)∠1的邻补角是( )
A.∠AOF B.∠BOE和∠AOF
C.∠BOC D.∠BOC和∠AOF
B
l2
l1
O
1
2
3
4
∠1的对顶角是______;
∠4的对顶角是______.
∠3
∠2
300
解:由邻补角的定义,得
∠2=180°-∠1=180°-50°=130°;
由对顶角相等,得
∠3=∠1=50°,∠4=∠2=130°.
变式1 如图,直线AB,CD相交于点O,射线OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为 ,
∠BOE的邻补角为 ;
∠BOD
∠AOE
(2)若∠AOC=70°,且∠BOE∶∠EOD=3∶4,
求∠AOE的度数.
解:∵∠BOD=∠AOC=70°,
∵∠BOD=∠BOE+∠EOD,
∵∠BOE∶∠EOD=3∶4,
∴∠BOE=70°÷7×3=300
∴∠AOE=180°-∠BOE=150°.
如图,直线a,b相交,若∠2是∠1的3倍,求∠1,∠2,∠3,∠4的度数.
完成推理过程.如图,直线a,b相交.
证明:∵∠1+∠2 = ,
∠2+∠3 = (邻补角定义)
∴∠1=1800- ,
∠3 =1800- (等式性质)
∴∠1=∠3 (等量代换)
由上面推理可知,对顶角的性质:对顶角 .
定义 图例 性质 几何语言
邻补角 有一条公共边,另一边互为反向延长线的两个角. 邻补角____ ∵∠1与∠2是邻补角∴__________
对顶角 有公共顶点,一角的两边与另一角的两边互为反向延长线. 对顶角_____ ∵∠1与∠3是对顶角∴__________
1.如下图所示,∠1和∠2是对顶角的图形有( ).
A.1个 B.2个 C.3个 D.4个
2.下面∠1和∠2不是邻补角的是( )
3.如图是一把剪刀,若∠AOB+∠COD=82°,则∠BOD= .
4.如图所示,直线AB,CD相交于点O,∠AOC∶∠AOD=2∶3,则∠BOD= °.
5.三条直线AB,CD,EF相交于一点O,
①∠AOD的对顶角是_____,
②∠AOC的邻补角是_______,
③若∠AOC=30°,则∠BOD=______,
∠COB=_______,
∠AOE+∠DOB+∠COF=_____
6.图中是对顶角量角器,用它测量角的原理是 .
7.如图5-1-12,直线AB和CD相交于点O,若∠BOD=40°,OA平分∠EOC,求∠EOD的度数.
