山东省东营市2022-2023学年 九年级下学期数学开学考试测试卷(含解析)
文档属性
| 名称 | 山东省东营市2022-2023学年 九年级下学期数学开学考试测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 624.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-06 14:22:28 | ||
图片预览



文档简介
山东省东营市2022-2023学年第二学期九年级数学开学考试测试卷(附答案)
一.选择题(共30分)
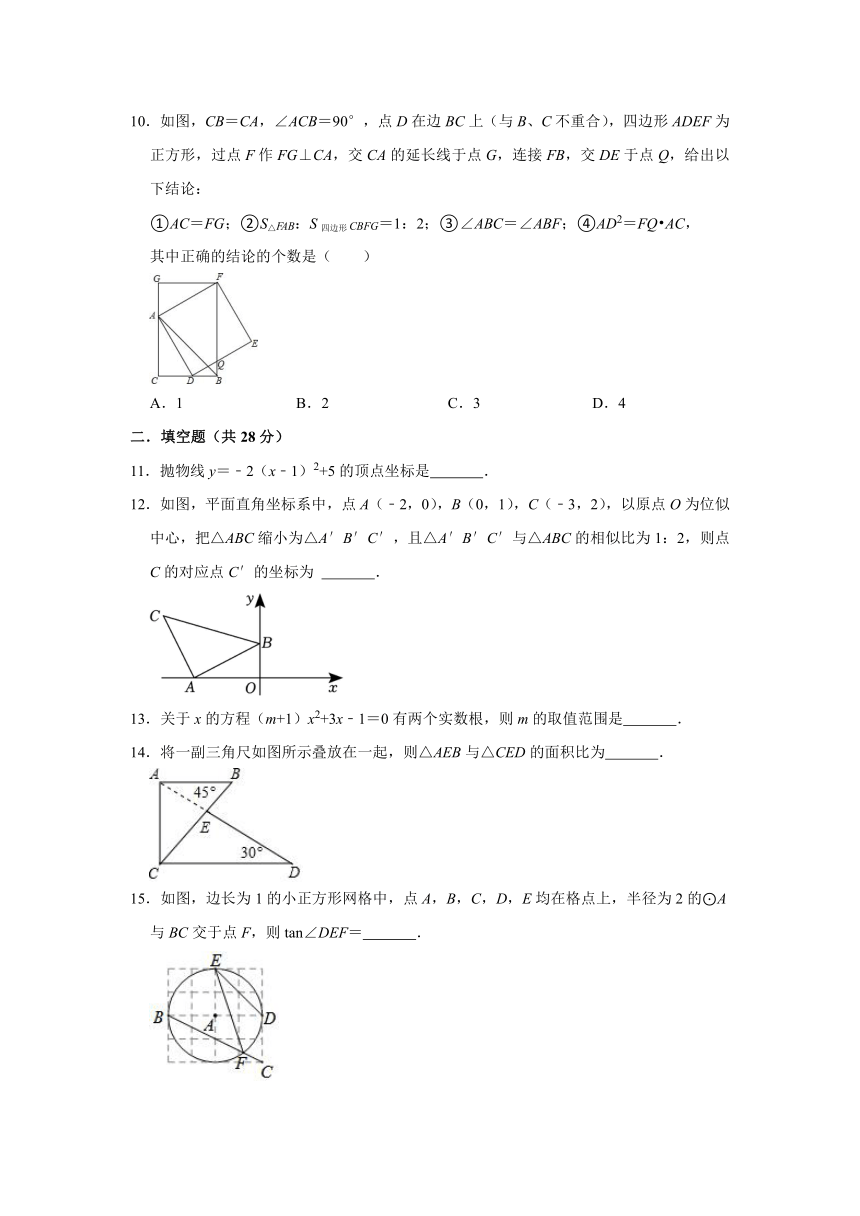
1.如所示四个图案中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.在下列函数中,y是x的反比例函数的是( )
A.y=3x B.y= C.y= D.y=
3.如图所示的几何体的主视图是( )
A. B. C. D.
4.如图,点A,B,C,D在圆O,AC是圆O的直径,∠CAD=26°,则∠ABD的度数为( )
A.26° B.52° C.64° D.74°
5.如图,l1∥l2∥l3,直线AB,CD与l1、l2、l3分别相交于点A、O、B和点C、O、D.若,CD=6,则CO的长是( )
A.2.4 B.3 C.3.6 D.4
6.如图,抛物线y=ax2+bx+c(a≠0)交x轴于点A,B,交y轴于点C.若点A坐标为(﹣4,0),对称轴为直线x=﹣1,则下列结论错误的是( )
A.二次函数的最大值为a﹣b+c
B.a+b+c>0
C.b2﹣4ac>0
D.2a+b=0
7.新型冠状病毒肺炎具有人传人性,调查发现1人感染病毒后如果不隔离,那么经过两轮传染将会有225人感染,若设1人平均感染x人,则x为( )
A.14 B.15 C.16 D.17
8.如图,从半径为9cm的圆形纸片中剪去一个扇形,使剪去的扇形的弧长为圆周长的,将留下的扇形纸片围成一个圆锥(接缝处不重叠),则这个圆锥的高为( )
A.6cm B.3cm C.8cm D.5cm
9.如图,已知A(,y1),B(2,y2)为反比例函数y=图象上的两点,动点P(x,0)在x轴的正半轴上运动,当线段AP与线段BP之差达到最大时点P的坐标是( )
A.(,0) B.(3,0) C.(4,0) D.(,0)
10.如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ AC,
其中正确的结论的个数是( )
A.1 B.2 C.3 D.4
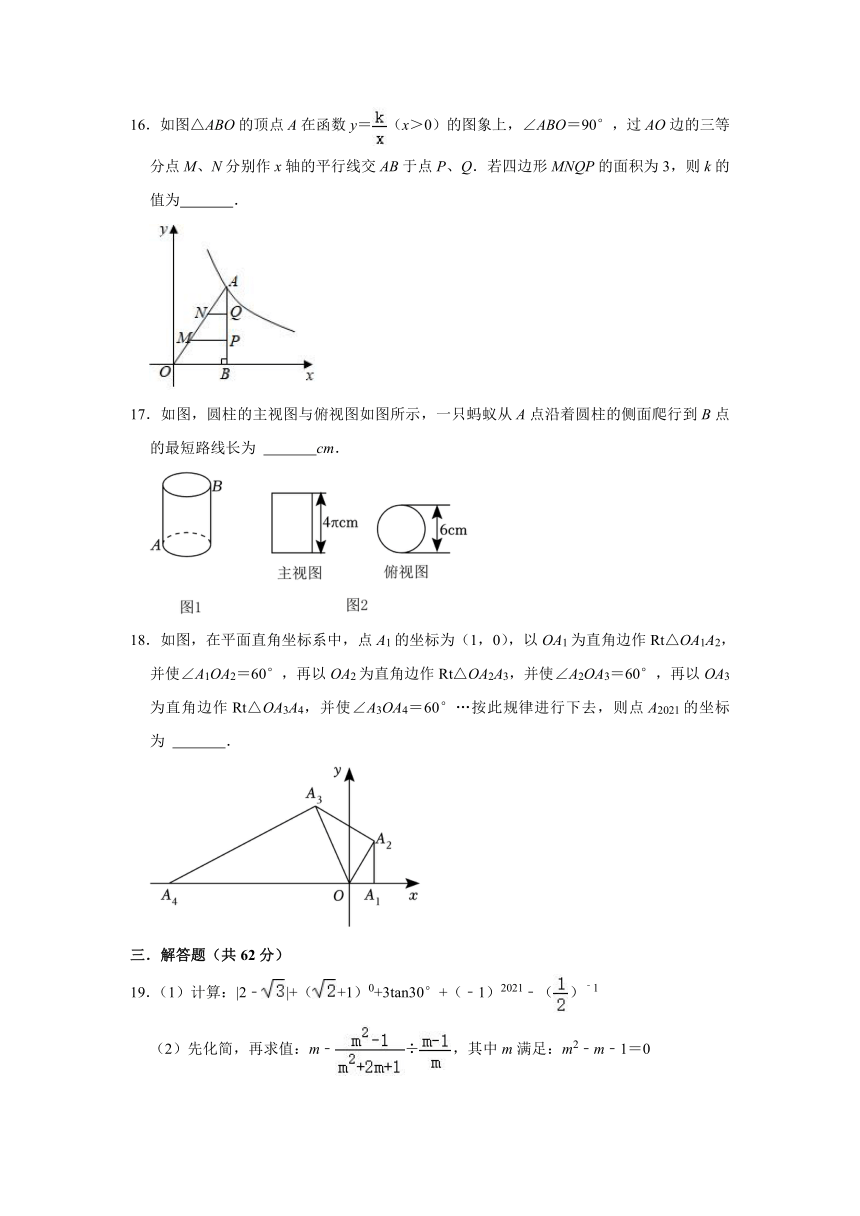
二.填空题(共28分)
11.抛物线y=﹣2(x﹣1)2+5的顶点坐标是 .
12.如图,平面直角坐标系中,点A(﹣2,0),B(0,1),C(﹣3,2),以原点O为位似中心,把△ABC缩小为△A′B′C′,且△A′B′C′与△ABC的相似比为1:2,则点C的对应点C′的坐标为 .
13.关于x的方程(m+1)x2+3x﹣1=0有两个实数根,则m的取值范围是 .
14.将一副三角尺如图所示叠放在一起,则△AEB与△CED的面积比为 .
15.如图,边长为1的小正方形网格中,点A,B,C,D,E均在格点上,半径为2的⊙A与BC交于点F,则tan∠DEF= .
16.如图△ABO的顶点A在函数y=(x>0)的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q.若四边形MNQP的面积为3,则k的值为 .
17.如图,圆柱的主视图与俯视图如图所示,一只蚂蚁从A点沿着圆柱的侧面爬行到B点的最短路线长为 cm.
18.如图,在平面直角坐标系中,点A1的坐标为(1,0),以OA1为直角边作Rt△OA1A2,并使∠A1OA2=60°,再以OA2为直角边作Rt△OA2A3,并使∠A2OA3=60°,再以OA3为直角边作Rt△OA3A4,并使∠A3OA4=60°…按此规律进行下去,则点A2021的坐标为 .
三.解答题(共62分)
19.(1)计算:|2﹣|+(+1)0+3tan30°+(﹣1)2021﹣()﹣1
(2)先化简,再求值:m﹣÷,其中m满足:m2﹣m﹣1=0
20.某班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
类别 频数(人数) 频率
小说 ① 0.5
戏剧 4 ②
散文 10 0.25
其他 6 ③
合计 ④ 1
根据图表提供的信息,解答下列问题:
(1)该班有 名学生,阅读小说类的有 名学生;
(2)求出扇形统计图中“其他类”和“戏剧类”分别所占的百分比;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.
21.如图,小华和同伴秋游时,发现在某地小山坡的点E处有一棵小树,他们想利用皮尺.测倾器和平面镜测量小树到山脚下的距离(即DE的长度),小华站在点B处,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E.且测得BC=6米,CD=22米,∠CDE=135°.已知小华的身高AB=1.6米,请根据以上数据,求DE的长度.(结果保留根号)
22.如图,在平面直角坐标系中,直线y=﹣x与反比例函数y=(k≠0)在第二象限内的图象相交于点A(m,1).
(1)求反比例函数的解析式;
(2)将直线y=﹣x向上平移后与反比例函数图象在第二象限内交于点B,与y轴交于点C,且△ABO的面积为,求直线BC的解析式.
23.如图,已知△ABC中,以AB为直径的⊙O交AC于点D,∠CBD=∠A.
(1)求证:BC为⊙O的切线;
(2)若E为中点,BD=12,sin∠BED=,求BE的长.
24.如图,抛物线y=ax2+bx+4交x轴于A(﹣3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.M为线段OB上的一个动点,过点M作PM⊥x轴,交抛物线于点P,交BC于点Q.
(1)求抛物线的表达式;
(2)过点P作PN⊥BC,垂足为点N.设M点的坐标为M(m,0),请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?
25.【问题情境】在△ABC中,BA=BC,∠ABC=α(0°<α<180°),点P为直线BC上一动点(不与点B、C重合),连接AP,将线段PA绕点P顺时针旋转得到线段PQ旋转角为α,连接CQ.
【特例分析】(1)当α=90°,点P在线段BC上时,过P作PF∥AC交直线AB于点F,如图①,易得图中与△APF全等的一个三角形是 ,∠ACQ= °.
【拓展探究】(2)当点P在BC延长线上,AB:AC=m:n时,如图②,试求线段BP与CQ的比值;
【问题解决】(3)当点P在直线BC上,α=60°,∠APB=30°,CP=4时,请直接写出线段CQ的长.
参考答案
一.选择题(共30分)
1.解:A.该图形是轴对称图形,不是中心对称图形,故此选项不合题意;
B.该图形是中心对称图形,不是轴对称图形,故此选项不合题意;
C.该图形是轴对称图形,不是中心对称图形,故此选项不合题意;
D.该图形既是轴对称图形,又是中心对称图形,故此选项符合题意.
故选:D.
2.解:A、该函数是正比例函数,故本选项错误;
B、该函数是正比例函数,故本选项错误;
C、该函数是符合反比例函数的定义,故本选项正确;
D、y是(x﹣1)反比例函数,故本选项错误;
故选:C.
3.解:从正面看易得底层是一个矩形,上层的左边是一个小矩形,左齐.
故选:D.
4.解:∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠ACD=90°﹣∠CAD=90°﹣26°=64°,
∴∠ABD=∠ACD=64°.
故选:C.
5.解:∵l1∥l2∥l3,
∴,
∴,
即,
∴CO=3.6,
故选:C.
6.解:当x=﹣1时,y=a﹣b+c的值最大,选项A不符合题意;
抛物线与x轴的另一个交点为(2,0),
当x=1时,y=a+b+c>0,因此选项B不符合题意;
抛物线与x轴有两个不同交点,因此b2﹣4ac>0,故选项C不符合题意;
抛物线y=ax2+bx+c过点A(﹣4,0),对称轴为直线x=﹣1,
因此有:x=﹣1=﹣,即2a﹣b=0,因此选项D符合题意;
故选:D.
7.解:设1人平均感染x人,
依题意可列方程:(1+x)2=225.
解得:x1=14,x2=﹣16(不合题意舍去),
即:x=14,
故选:A.
8.解:∵从半径为9cm的圆形纸片剪去圆周的一个扇形,
∴留下的扇形圆心角为:360°×=240°,
∴留下的扇形的弧长==12π,
根据底面圆的周长等于扇形弧长,
∴圆锥的底面半径r==6cm,
所以圆锥的高==3cm.
故选:B.
9.解:∵A(,y1),B(2,y2)为反比例函数y=图象上的两点,
∴y1=2,y2=,
∵动点P(x,0)在x轴的正半轴上运动,|AP﹣BP|<AB,
∴延长AB交x轴于点P′,当点P在点P′时,PA﹣PB=AB达到最大值,
设直线AB的函数解析式为y=kx+b,
,得,
∴直线AB的函数解析式为y=﹣x+,
当y=0时,x=,
∴当线段AP与线段BP之差达到最大时点P的坐标是(,0),
故选:D.
10.解:∵四边形ADEF为正方形,
∴∠FAD=90°,AD=AF=EF,
∴∠CAD+∠FAG=90°,
∵FG⊥CA,
∴∠GAF+∠AFG=90°,
∴∠CAD=∠AFG,
在△FGA和△ACD中,,
∴△FGA≌△ACD(AAS),
∴AC=FG,①正确;
∵BC=AC,
∴FG=BC,
∵∠ACB=90°,FG⊥CA,
∴FG∥BC,
∴四边形CBFG是矩形,
∴∠CBF=90°,S△FAB=FB FG=S四边形CBFG,②正确;
∵CA=CB,∠C=∠CBF=90°,
∴∠ABC=∠ABF=45°,③正确;
∵四边形ADEF为正方形,
∴∠ADE=∠QBD=∠E=90°,
∴∠ADC+∠QDB=90°,
∵∠QDB+∠DQB=90°,
∴∠FQE=∠DQB=∠ADC,
∵∠E=∠C=90°,
∴△ACD∽△FEQ,
∴AC:AD=FE:FQ,
∴AD FE=AD2=FQ AC,④正确;
或:AD2表示正方形的面积;连接AQ,FQ×AC=FQ×BC=FQ×GF=△AFQ面积的2倍(FQ为底,GF为高)=△AFQ面积的2倍(AF为底,AD为高)=正方形的面积,所以结论4是对的;
故选:D.
二.填空题(共28分)
11.解:抛物线y=﹣2(x﹣1)2+5的顶点坐标是(1,5).
故答案为:(1,5).
12.解:以原点O为位似中心,把△ABC缩小为△A′B′C′,且△A′B′C′与△ABC的相似比为1:2,
∵点C的坐标为(﹣3,2),
∴点C的对应点C′的坐标为(﹣3×,2×)或(3×,﹣2×),即(﹣1.5,1)或(1.5,﹣1),
故答案为:(﹣1.5,1)或(1.5,﹣1),
13.解:∵关于x的方程(m+1)x2+3x﹣1=0有两个实数根,
∴Δ=9+4(m+1)≥0,且m+1≠0,
解得:m≥﹣且m≠﹣1.
故答案为:m≥﹣且m≠﹣1.
14.解:∵∠BAC=∠ACD=90°,
∴AB∥CD.
∴△ABE∽△DCE.
∴=.
∵在Rt△ACB中∠B=45°,
∴AB=AC.
∵在Rt△ACD中,∠D=30°,
∴CD==AC.
∴==.
∴=()2=()2=.
故答案是:.
15.解:由题意可得:∠DBC=∠DEF,
则tan∠DEF=tan∠DBC==.
故答案为:.
16.解:∵NQ∥MP∥OB,
∴△ANQ∽△AMP∽△AOB,
∵M、N是OA的三等分点,
∴=,=,
∴=,
∵四边形MNQP的面积为3,
∴=,
∴S△ANQ=1,
∵=()2=,
∴S△AOB=9,
∴k=2S△AOB=18,
故答案为:18.
17.解:把圆柱侧面展开,展开图如图所示,点A,B的最短距离为线段AB的长,
∵BC=4πcm,AC为底面半圆弧长,即AC=×6 π=3π(cm),
∴AB==5π(cm).
故答案为:5π.
18.解:由题意得,A1的坐标为(1,0),A2的坐标为(1,),A3的坐标为( 2,2),A4的坐标为( 8,0),A5的坐标为( 8, 8),A6的坐标为(16, 16),A7的坐标为(64,0),
…
由上可知,A点的方位是每6个循环,
与第一点方位相同的点在x轴正半轴上,其横坐标为2n﹣1,其纵坐标为0,
与第二点方位相同的点在第一象限内,其横坐标为2n﹣2,纵坐标为2n﹣2,
与第三点方位相同的点在第二象限内,其横坐标为﹣2n﹣2,纵坐标为2n﹣2,
与第四点方位相同的点在x轴负半轴上,其横坐标为﹣2n﹣1,纵坐标为0,
与第五点方位相同的点在第三象限内,其横坐标为﹣2n﹣2,纵坐标为﹣2n﹣2,
与第六点方位相同的点在第四象限内,其横坐标为2n﹣2,纵坐标为﹣2n﹣2,
∵2021÷6=336…5,
∴点A2021的方位与点A5的方位相同,在第三象限内,其横坐标为﹣2n﹣2=﹣22019,纵坐标为,
故答案为:(﹣22019,).
三.解答题(共62分)
19.解:(1)|2﹣|+(+1)0+3tan30°+(﹣1)2021﹣()﹣1
=2﹣+1+3×+(﹣1)﹣2
=2﹣+1++(﹣1)﹣2
=0;
(2)m﹣÷=m﹣ =m﹣==,
∵m2﹣m﹣1=0,
∴m2=m+1,
∴原式==1.
20.解:(1)10÷0.25=40(名),
40×50%=20(名),
故答案为:40,20;
(2)扇形统计图中“其他”类所占的百分比为:6÷40×100%=15%,
“戏剧”类所占的百分比4÷40×100%=10%;
(3)树状图如下图所示,
由上可得,一共有12种可能性,其中选取的是乙和丙的有两种可能性,
故选取的2人恰好是乙和丙的概率为=.
21.解:过E作EF⊥BC于F,
∵∠CDE=135°,
∴∠EDF=45°,
设EF为x米,DF=x米,DE=x米,
∵∠B=∠EFC=90°,
∵∠ACB=∠ECD,
∴△ABC∽△EFC,
∴,
即=,
解得:x=8,
∴DE=8,
答:DE的长度为8米.
22.解:(1)∵直线y=﹣x过点A(m,1),
∴﹣m=1,解得m=﹣2,
∴A(﹣2,1).
∵反比例函数y=(k≠0)的图象过点A(﹣2,1),
∴k=﹣2×1=﹣2,
∴反比例函数的解析式为y=﹣;
(2)设直线BC的解析式为y=﹣x+b,
∵三角形ACO与三角形ABO面积相等,且△ABO的面积为,
∴△ACO的面积=OC 2=,
∴OC=,
∴b=,
∴直线BC的解析式为y=﹣x+.
23.(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠A+∠ABD=90°.
又∵∠A=∠CBD,
∴∠CBD+∠ABD=90°.
∴∠ABC=90°.
∴AB⊥BC.
又∵AB是⊙O的直径,
∴BC为⊙O的切线.
(2)解:连接AE.如图所示:
∵AB是⊙O的直径,
∴∠AEB=∠ADB=90°.
∵∠BAD=∠BED,
∴sin∠BAD=sin∠BED=.
∴在Rt△ABD中,sin∠BAD==,
∵BD=12,
∴AB=20.
∵E为的中点,
∴AE=BE.
∴△AEB是等腰直角三角形.
∴∠BAE=45°.
∴BE=AB×sin∠BAE=20×=10.
24.解:(1)将A(﹣3,0),B(4,0)代入y=ax2+bx+4,得,
解之,得.
所以,抛物线的表达式为;
(2)由,得C(0,4).
将点B(4,0)、C(0,4)代入y=kx+b,得,解之,得.
所以,直线BC的表达式为:y=﹣x+4.
由M(m,0),得,Q(m,﹣m+4).
∴,
∵OB=OC,
∴∠ABC=∠OCB=45°.
∴∠PQN=∠BQM=45°.
∴=.
∵,
∴当m=2时,PN有最大值,最大值为.
25.解:(1)如图①,∵∠ABC=90°,AB=CB,
∴△ABC是等腰直角三角形,
∵PF∥AC,
∴∠BPF=∠BFP=45°,
∴△BPF是等腰直角三角形,
∴BF=BP,
∴AF=CP,
由旋转可得,AP=PQ,∠APQ=90°,而∠BPF=45°,
∴∠QPC=45°﹣∠APF,
又∵∠PAF=∠PFB﹣∠APF=45°﹣∠APF,
∴∠PAF=∠QPC,
∴△APF≌△PQC,
∴∠PCQ=∠AFP=135°,
又∵∠ACB=45°,
∴∠ACQ=90°,
故答案为:△PQC,90;
(2)如图②,过P作PF∥AC,交BA的延长线于F,则=,
又∵AB=BC,
∴AF=CP,
又∵∠FAP=∠ABC+∠APB=α+∠APB,∠CPQ=∠APQ+∠APB=α+∠APB,
∴∠FAP=∠CPQ,
由旋转可得,PA=PQ,
∴△AFP≌△PCQ,
∴FP=CQ,
∵PF∥AC,
∴△ABC∽△FBP,
∴=,
∴====;
(3)如图,当P在CB的延长线上时,
∠CPQ=∠APQ﹣∠APB=60°﹣30°=30°,
∴∠APC=∠QPC,
又∵AP=QP,PC=PC,
∴△APC≌△QPC,
∴CQ=AC,
又∵BA=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠ABC=60°,∠BAP=∠ABC﹣∠APB=30°,
∴BP=AB=BC=PC=2,
∴QC=AC=BC=2;
如图,当P在BC的延长线上时,连接AQ,
由旋转可得,AP=QP,∠APQ=∠ABC=60°,
∴△APQ是等边三角形,
∴AQ=PQ,∠APQ=60°=∠AQP,
又∵∠APB=30°,∠ACB=60°,
∴∠CAP=30°,∠CPQ=90°,
∴∠CAP=∠APA,
∴AC=PC,
∴△ACQ≌△PCQ,
∴∠AQC=∠PQC=∠AQP=30°,
∴Rt△PCQ中,CQ=2CP=8.
综上所述,线段CQ的长为2或8.
一.选择题(共30分)
1.如所示四个图案中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.在下列函数中,y是x的反比例函数的是( )
A.y=3x B.y= C.y= D.y=
3.如图所示的几何体的主视图是( )
A. B. C. D.
4.如图,点A,B,C,D在圆O,AC是圆O的直径,∠CAD=26°,则∠ABD的度数为( )
A.26° B.52° C.64° D.74°
5.如图,l1∥l2∥l3,直线AB,CD与l1、l2、l3分别相交于点A、O、B和点C、O、D.若,CD=6,则CO的长是( )
A.2.4 B.3 C.3.6 D.4
6.如图,抛物线y=ax2+bx+c(a≠0)交x轴于点A,B,交y轴于点C.若点A坐标为(﹣4,0),对称轴为直线x=﹣1,则下列结论错误的是( )
A.二次函数的最大值为a﹣b+c
B.a+b+c>0
C.b2﹣4ac>0
D.2a+b=0
7.新型冠状病毒肺炎具有人传人性,调查发现1人感染病毒后如果不隔离,那么经过两轮传染将会有225人感染,若设1人平均感染x人,则x为( )
A.14 B.15 C.16 D.17
8.如图,从半径为9cm的圆形纸片中剪去一个扇形,使剪去的扇形的弧长为圆周长的,将留下的扇形纸片围成一个圆锥(接缝处不重叠),则这个圆锥的高为( )
A.6cm B.3cm C.8cm D.5cm
9.如图,已知A(,y1),B(2,y2)为反比例函数y=图象上的两点,动点P(x,0)在x轴的正半轴上运动,当线段AP与线段BP之差达到最大时点P的坐标是( )
A.(,0) B.(3,0) C.(4,0) D.(,0)
10.如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ AC,
其中正确的结论的个数是( )
A.1 B.2 C.3 D.4
二.填空题(共28分)
11.抛物线y=﹣2(x﹣1)2+5的顶点坐标是 .
12.如图,平面直角坐标系中,点A(﹣2,0),B(0,1),C(﹣3,2),以原点O为位似中心,把△ABC缩小为△A′B′C′,且△A′B′C′与△ABC的相似比为1:2,则点C的对应点C′的坐标为 .
13.关于x的方程(m+1)x2+3x﹣1=0有两个实数根,则m的取值范围是 .
14.将一副三角尺如图所示叠放在一起,则△AEB与△CED的面积比为 .
15.如图,边长为1的小正方形网格中,点A,B,C,D,E均在格点上,半径为2的⊙A与BC交于点F,则tan∠DEF= .
16.如图△ABO的顶点A在函数y=(x>0)的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q.若四边形MNQP的面积为3,则k的值为 .
17.如图,圆柱的主视图与俯视图如图所示,一只蚂蚁从A点沿着圆柱的侧面爬行到B点的最短路线长为 cm.
18.如图,在平面直角坐标系中,点A1的坐标为(1,0),以OA1为直角边作Rt△OA1A2,并使∠A1OA2=60°,再以OA2为直角边作Rt△OA2A3,并使∠A2OA3=60°,再以OA3为直角边作Rt△OA3A4,并使∠A3OA4=60°…按此规律进行下去,则点A2021的坐标为 .
三.解答题(共62分)
19.(1)计算:|2﹣|+(+1)0+3tan30°+(﹣1)2021﹣()﹣1
(2)先化简,再求值:m﹣÷,其中m满足:m2﹣m﹣1=0
20.某班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
类别 频数(人数) 频率
小说 ① 0.5
戏剧 4 ②
散文 10 0.25
其他 6 ③
合计 ④ 1
根据图表提供的信息,解答下列问题:
(1)该班有 名学生,阅读小说类的有 名学生;
(2)求出扇形统计图中“其他类”和“戏剧类”分别所占的百分比;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.
21.如图,小华和同伴秋游时,发现在某地小山坡的点E处有一棵小树,他们想利用皮尺.测倾器和平面镜测量小树到山脚下的距离(即DE的长度),小华站在点B处,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E.且测得BC=6米,CD=22米,∠CDE=135°.已知小华的身高AB=1.6米,请根据以上数据,求DE的长度.(结果保留根号)
22.如图,在平面直角坐标系中,直线y=﹣x与反比例函数y=(k≠0)在第二象限内的图象相交于点A(m,1).
(1)求反比例函数的解析式;
(2)将直线y=﹣x向上平移后与反比例函数图象在第二象限内交于点B,与y轴交于点C,且△ABO的面积为,求直线BC的解析式.
23.如图,已知△ABC中,以AB为直径的⊙O交AC于点D,∠CBD=∠A.
(1)求证:BC为⊙O的切线;
(2)若E为中点,BD=12,sin∠BED=,求BE的长.
24.如图,抛物线y=ax2+bx+4交x轴于A(﹣3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.M为线段OB上的一个动点,过点M作PM⊥x轴,交抛物线于点P,交BC于点Q.
(1)求抛物线的表达式;
(2)过点P作PN⊥BC,垂足为点N.设M点的坐标为M(m,0),请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?
25.【问题情境】在△ABC中,BA=BC,∠ABC=α(0°<α<180°),点P为直线BC上一动点(不与点B、C重合),连接AP,将线段PA绕点P顺时针旋转得到线段PQ旋转角为α,连接CQ.
【特例分析】(1)当α=90°,点P在线段BC上时,过P作PF∥AC交直线AB于点F,如图①,易得图中与△APF全等的一个三角形是 ,∠ACQ= °.
【拓展探究】(2)当点P在BC延长线上,AB:AC=m:n时,如图②,试求线段BP与CQ的比值;
【问题解决】(3)当点P在直线BC上,α=60°,∠APB=30°,CP=4时,请直接写出线段CQ的长.
参考答案
一.选择题(共30分)
1.解:A.该图形是轴对称图形,不是中心对称图形,故此选项不合题意;
B.该图形是中心对称图形,不是轴对称图形,故此选项不合题意;
C.该图形是轴对称图形,不是中心对称图形,故此选项不合题意;
D.该图形既是轴对称图形,又是中心对称图形,故此选项符合题意.
故选:D.
2.解:A、该函数是正比例函数,故本选项错误;
B、该函数是正比例函数,故本选项错误;
C、该函数是符合反比例函数的定义,故本选项正确;
D、y是(x﹣1)反比例函数,故本选项错误;
故选:C.
3.解:从正面看易得底层是一个矩形,上层的左边是一个小矩形,左齐.
故选:D.
4.解:∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠ACD=90°﹣∠CAD=90°﹣26°=64°,
∴∠ABD=∠ACD=64°.
故选:C.
5.解:∵l1∥l2∥l3,
∴,
∴,
即,
∴CO=3.6,
故选:C.
6.解:当x=﹣1时,y=a﹣b+c的值最大,选项A不符合题意;
抛物线与x轴的另一个交点为(2,0),
当x=1时,y=a+b+c>0,因此选项B不符合题意;
抛物线与x轴有两个不同交点,因此b2﹣4ac>0,故选项C不符合题意;
抛物线y=ax2+bx+c过点A(﹣4,0),对称轴为直线x=﹣1,
因此有:x=﹣1=﹣,即2a﹣b=0,因此选项D符合题意;
故选:D.
7.解:设1人平均感染x人,
依题意可列方程:(1+x)2=225.
解得:x1=14,x2=﹣16(不合题意舍去),
即:x=14,
故选:A.
8.解:∵从半径为9cm的圆形纸片剪去圆周的一个扇形,
∴留下的扇形圆心角为:360°×=240°,
∴留下的扇形的弧长==12π,
根据底面圆的周长等于扇形弧长,
∴圆锥的底面半径r==6cm,
所以圆锥的高==3cm.
故选:B.
9.解:∵A(,y1),B(2,y2)为反比例函数y=图象上的两点,
∴y1=2,y2=,
∵动点P(x,0)在x轴的正半轴上运动,|AP﹣BP|<AB,
∴延长AB交x轴于点P′,当点P在点P′时,PA﹣PB=AB达到最大值,
设直线AB的函数解析式为y=kx+b,
,得,
∴直线AB的函数解析式为y=﹣x+,
当y=0时,x=,
∴当线段AP与线段BP之差达到最大时点P的坐标是(,0),
故选:D.
10.解:∵四边形ADEF为正方形,
∴∠FAD=90°,AD=AF=EF,
∴∠CAD+∠FAG=90°,
∵FG⊥CA,
∴∠GAF+∠AFG=90°,
∴∠CAD=∠AFG,
在△FGA和△ACD中,,
∴△FGA≌△ACD(AAS),
∴AC=FG,①正确;
∵BC=AC,
∴FG=BC,
∵∠ACB=90°,FG⊥CA,
∴FG∥BC,
∴四边形CBFG是矩形,
∴∠CBF=90°,S△FAB=FB FG=S四边形CBFG,②正确;
∵CA=CB,∠C=∠CBF=90°,
∴∠ABC=∠ABF=45°,③正确;
∵四边形ADEF为正方形,
∴∠ADE=∠QBD=∠E=90°,
∴∠ADC+∠QDB=90°,
∵∠QDB+∠DQB=90°,
∴∠FQE=∠DQB=∠ADC,
∵∠E=∠C=90°,
∴△ACD∽△FEQ,
∴AC:AD=FE:FQ,
∴AD FE=AD2=FQ AC,④正确;
或:AD2表示正方形的面积;连接AQ,FQ×AC=FQ×BC=FQ×GF=△AFQ面积的2倍(FQ为底,GF为高)=△AFQ面积的2倍(AF为底,AD为高)=正方形的面积,所以结论4是对的;
故选:D.
二.填空题(共28分)
11.解:抛物线y=﹣2(x﹣1)2+5的顶点坐标是(1,5).
故答案为:(1,5).
12.解:以原点O为位似中心,把△ABC缩小为△A′B′C′,且△A′B′C′与△ABC的相似比为1:2,
∵点C的坐标为(﹣3,2),
∴点C的对应点C′的坐标为(﹣3×,2×)或(3×,﹣2×),即(﹣1.5,1)或(1.5,﹣1),
故答案为:(﹣1.5,1)或(1.5,﹣1),
13.解:∵关于x的方程(m+1)x2+3x﹣1=0有两个实数根,
∴Δ=9+4(m+1)≥0,且m+1≠0,
解得:m≥﹣且m≠﹣1.
故答案为:m≥﹣且m≠﹣1.
14.解:∵∠BAC=∠ACD=90°,
∴AB∥CD.
∴△ABE∽△DCE.
∴=.
∵在Rt△ACB中∠B=45°,
∴AB=AC.
∵在Rt△ACD中,∠D=30°,
∴CD==AC.
∴==.
∴=()2=()2=.
故答案是:.
15.解:由题意可得:∠DBC=∠DEF,
则tan∠DEF=tan∠DBC==.
故答案为:.
16.解:∵NQ∥MP∥OB,
∴△ANQ∽△AMP∽△AOB,
∵M、N是OA的三等分点,
∴=,=,
∴=,
∵四边形MNQP的面积为3,
∴=,
∴S△ANQ=1,
∵=()2=,
∴S△AOB=9,
∴k=2S△AOB=18,
故答案为:18.
17.解:把圆柱侧面展开,展开图如图所示,点A,B的最短距离为线段AB的长,
∵BC=4πcm,AC为底面半圆弧长,即AC=×6 π=3π(cm),
∴AB==5π(cm).
故答案为:5π.
18.解:由题意得,A1的坐标为(1,0),A2的坐标为(1,),A3的坐标为( 2,2),A4的坐标为( 8,0),A5的坐标为( 8, 8),A6的坐标为(16, 16),A7的坐标为(64,0),
…
由上可知,A点的方位是每6个循环,
与第一点方位相同的点在x轴正半轴上,其横坐标为2n﹣1,其纵坐标为0,
与第二点方位相同的点在第一象限内,其横坐标为2n﹣2,纵坐标为2n﹣2,
与第三点方位相同的点在第二象限内,其横坐标为﹣2n﹣2,纵坐标为2n﹣2,
与第四点方位相同的点在x轴负半轴上,其横坐标为﹣2n﹣1,纵坐标为0,
与第五点方位相同的点在第三象限内,其横坐标为﹣2n﹣2,纵坐标为﹣2n﹣2,
与第六点方位相同的点在第四象限内,其横坐标为2n﹣2,纵坐标为﹣2n﹣2,
∵2021÷6=336…5,
∴点A2021的方位与点A5的方位相同,在第三象限内,其横坐标为﹣2n﹣2=﹣22019,纵坐标为,
故答案为:(﹣22019,).
三.解答题(共62分)
19.解:(1)|2﹣|+(+1)0+3tan30°+(﹣1)2021﹣()﹣1
=2﹣+1+3×+(﹣1)﹣2
=2﹣+1++(﹣1)﹣2
=0;
(2)m﹣÷=m﹣ =m﹣==,
∵m2﹣m﹣1=0,
∴m2=m+1,
∴原式==1.
20.解:(1)10÷0.25=40(名),
40×50%=20(名),
故答案为:40,20;
(2)扇形统计图中“其他”类所占的百分比为:6÷40×100%=15%,
“戏剧”类所占的百分比4÷40×100%=10%;
(3)树状图如下图所示,
由上可得,一共有12种可能性,其中选取的是乙和丙的有两种可能性,
故选取的2人恰好是乙和丙的概率为=.
21.解:过E作EF⊥BC于F,
∵∠CDE=135°,
∴∠EDF=45°,
设EF为x米,DF=x米,DE=x米,
∵∠B=∠EFC=90°,
∵∠ACB=∠ECD,
∴△ABC∽△EFC,
∴,
即=,
解得:x=8,
∴DE=8,
答:DE的长度为8米.
22.解:(1)∵直线y=﹣x过点A(m,1),
∴﹣m=1,解得m=﹣2,
∴A(﹣2,1).
∵反比例函数y=(k≠0)的图象过点A(﹣2,1),
∴k=﹣2×1=﹣2,
∴反比例函数的解析式为y=﹣;
(2)设直线BC的解析式为y=﹣x+b,
∵三角形ACO与三角形ABO面积相等,且△ABO的面积为,
∴△ACO的面积=OC 2=,
∴OC=,
∴b=,
∴直线BC的解析式为y=﹣x+.
23.(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠A+∠ABD=90°.
又∵∠A=∠CBD,
∴∠CBD+∠ABD=90°.
∴∠ABC=90°.
∴AB⊥BC.
又∵AB是⊙O的直径,
∴BC为⊙O的切线.
(2)解:连接AE.如图所示:
∵AB是⊙O的直径,
∴∠AEB=∠ADB=90°.
∵∠BAD=∠BED,
∴sin∠BAD=sin∠BED=.
∴在Rt△ABD中,sin∠BAD==,
∵BD=12,
∴AB=20.
∵E为的中点,
∴AE=BE.
∴△AEB是等腰直角三角形.
∴∠BAE=45°.
∴BE=AB×sin∠BAE=20×=10.
24.解:(1)将A(﹣3,0),B(4,0)代入y=ax2+bx+4,得,
解之,得.
所以,抛物线的表达式为;
(2)由,得C(0,4).
将点B(4,0)、C(0,4)代入y=kx+b,得,解之,得.
所以,直线BC的表达式为:y=﹣x+4.
由M(m,0),得,Q(m,﹣m+4).
∴,
∵OB=OC,
∴∠ABC=∠OCB=45°.
∴∠PQN=∠BQM=45°.
∴=.
∵,
∴当m=2时,PN有最大值,最大值为.
25.解:(1)如图①,∵∠ABC=90°,AB=CB,
∴△ABC是等腰直角三角形,
∵PF∥AC,
∴∠BPF=∠BFP=45°,
∴△BPF是等腰直角三角形,
∴BF=BP,
∴AF=CP,
由旋转可得,AP=PQ,∠APQ=90°,而∠BPF=45°,
∴∠QPC=45°﹣∠APF,
又∵∠PAF=∠PFB﹣∠APF=45°﹣∠APF,
∴∠PAF=∠QPC,
∴△APF≌△PQC,
∴∠PCQ=∠AFP=135°,
又∵∠ACB=45°,
∴∠ACQ=90°,
故答案为:△PQC,90;
(2)如图②,过P作PF∥AC,交BA的延长线于F,则=,
又∵AB=BC,
∴AF=CP,
又∵∠FAP=∠ABC+∠APB=α+∠APB,∠CPQ=∠APQ+∠APB=α+∠APB,
∴∠FAP=∠CPQ,
由旋转可得,PA=PQ,
∴△AFP≌△PCQ,
∴FP=CQ,
∵PF∥AC,
∴△ABC∽△FBP,
∴=,
∴====;
(3)如图,当P在CB的延长线上时,
∠CPQ=∠APQ﹣∠APB=60°﹣30°=30°,
∴∠APC=∠QPC,
又∵AP=QP,PC=PC,
∴△APC≌△QPC,
∴CQ=AC,
又∵BA=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠ABC=60°,∠BAP=∠ABC﹣∠APB=30°,
∴BP=AB=BC=PC=2,
∴QC=AC=BC=2;
如图,当P在BC的延长线上时,连接AQ,
由旋转可得,AP=QP,∠APQ=∠ABC=60°,
∴△APQ是等边三角形,
∴AQ=PQ,∠APQ=60°=∠AQP,
又∵∠APB=30°,∠ACB=60°,
∴∠CAP=30°,∠CPQ=90°,
∴∠CAP=∠APA,
∴AC=PC,
∴△ACQ≌△PCQ,
∴∠AQC=∠PQC=∠AQP=30°,
∴Rt△PCQ中,CQ=2CP=8.
综上所述,线段CQ的长为2或8.
同课章节目录
