第十四章 一次函数 一 函数和函数的图像 课后练习(无答案)2022-2023学年京改版八年级数学下册
文档属性
| 名称 | 第十四章 一次函数 一 函数和函数的图像 课后练习(无答案)2022-2023学年京改版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 478.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-05 20:28:06 | ||
图片预览



文档简介
第十四章 一次函数 一 函数和函数的图像课后练习
班级:________ 姓名:________
一、单选题(共 10 小题)
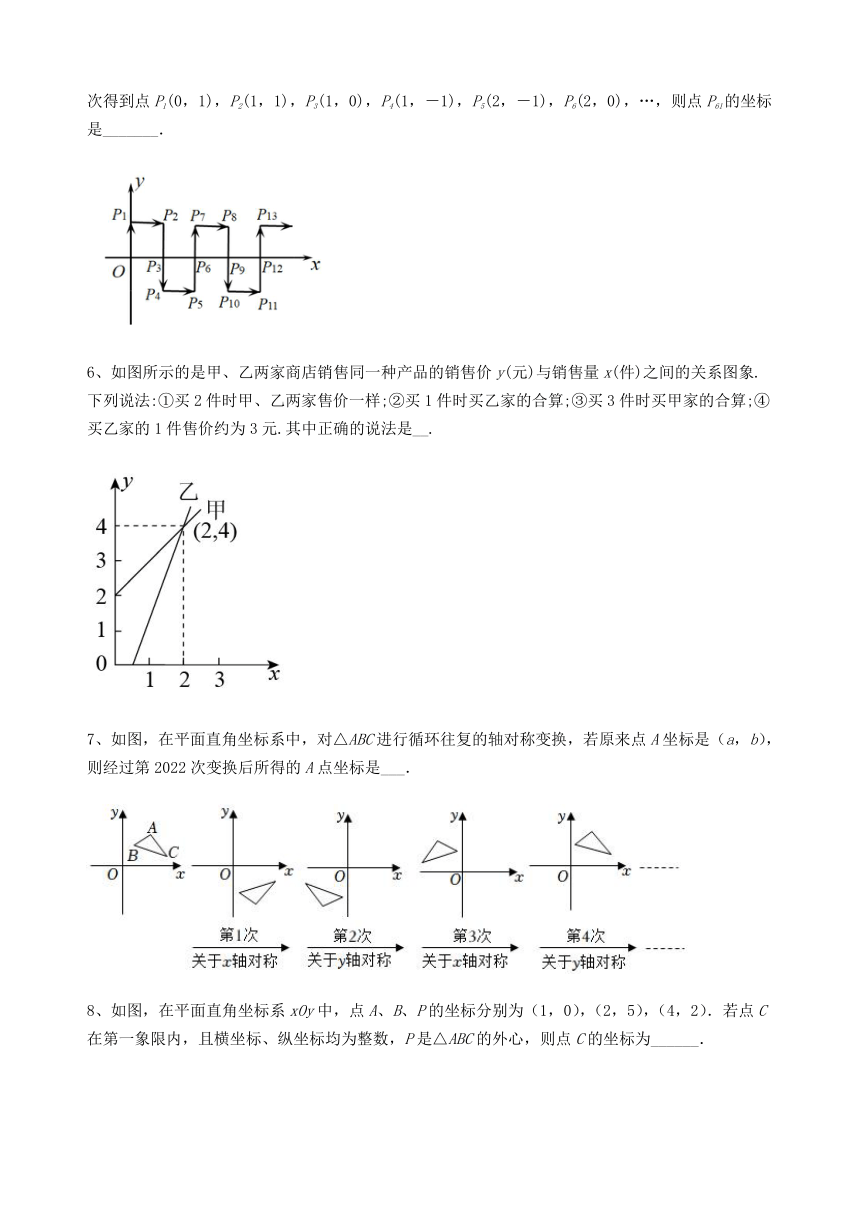
1、如图,,,点,,则点B的坐标是( )
A. B. C. D.
2、均匀的向一个容器内注水,在注水过程中,水面高度与时间的函数关系如图所示,则该容器是下列中的( )
A. B. C. D.
3、已知A、B两点的坐标分别是和,下列结论错误的是( )
A.点A在第二象限 B.点B在第一象限
C.线段平行于y轴 D.点A、B之间的距离为4
4、若点A(,)、点B(3,),且AB∥x轴,则AB的值为( )
A.2 B.3 C.4 D.5
5、在平面直角坐标系xoy中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,,点A2的伴随点为A3,,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(2,4),点A2020的坐标为( )
A.(-3,3) B.(-2,-2) C.(3,-1) D.(2,4)
6、如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为( )
A.(2,3) B.(0,3) C.(3,2) D.(2,2)
7、已知点,若直线轴,点P在x轴的负半轴上,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8、如图,直角坐标平面内,动点P按图中箭头所示方向依次运动,第1次从点运动到点,第2次运动到点,第3次运动到点,…,按这样的运动规律,动点P第2022次运动到点的坐标是( )
A. B. C. D.
9、当点A(x﹣1,3)到点B(﹣2,2y+5)的距离最短时,点P(x,y)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10、已知点关于原点的对称点在第四象限,则的取值范围在数轴上表示正确的是( )
A. B.
C. D.
二、填空题(共 10 小题)
1、若对于所有的实数,都有,则______.
2、若点P 关于原点的对称点Q在第三象限,那么m的取值范围是_______.
3、将一组数,,3,,,…..按下面的方式进行排列:
,,3,,;
,,,,;
.....
若的位置记为(1,4),的位置记为(2,3),则这组数中最大的有理数的位置记为_____.
4、如图,在平面直角坐标系中,点A,B,D的坐标为,,,点P从点B出发,沿﹣运动,速度为每秒1个单位长度,设运动时间为t秒;点Q以每秒2个单位长度的速度从点D出发,在DA间往返运动,(两个点同时出发,当点P到达点A停止时点Q也停止),在运动过程中,当时,点P的坐标为___________.
5、如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P61的坐标是_______.
6、如图所示的是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的关系图象.下列说法:①买2件时甲、乙两家售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买乙家的1件售价约为3元.其中正确的说法是__.
7、如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2022次变换后所得的A点坐标是___.
8、如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为______.
9、由图可知,在平面直角坐标系中,一块等腰直角三角板如图放置,其中,则点的坐标为___________;
10、如图,在平面直角坐标系中,以A(2,0),B(0,1)为顶点作等腰直角三角形ABC(其中∠ABC=90°,且点C落在第一象限),则点C关于y轴的对称点C'的坐标为______.
三、解答题(共 6 小题)
1、如图,是一个简单的平面示意图,已知OA=2km,OB=6km,OC=BD=4km,点E为OC的中点,回答下列问题:
(1)由图可知,高铁站在小明家南偏西65°方向6km处.请类似这种方法用方向与距离描述学校、博物馆相对于小明家的位置;
(2)图中到小明家距离相同的是哪些地方?
(3)若小强家在小明家北偏西60°方向2km处,请在图中标出小强家的位置.
2、在平面直角坐标系中,点从原点出发,沿轴正方向按折线不断向前运动,其移动路线如图所示.这时点,,,的坐标分别为,,,,,按照这个规律,解决下列问题:
(1)写出下列点的坐标: , , , ;
(2)点和点的位置分别在 , .(填轴上方、轴下方或轴上)
3、如图是小李骑自行车离家的距离s (km)与时间t (h) 之间的关系.
(1)在这个变化过程中自变量__________,因变量是__________,
(2)小李__________时到达离家最远的地方 此时离家________km;
(3)分别写出在1<t<2时和2<t<4时小李骑自行车的速度为______ km/h 和______km/h.
(4)小李______时与家相距20km.
4、如图,在平面直角坐标系中,已知三点,其中a、b满足关系式.
(1)求a、b、c的值;
(2)如果在第二象限内有一点,请用含m的式子表示四边形的面积;
(3)在(2)的条件下,是否存在点P,使四边形的面积与的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
5、小咏星期日上午8:00从家骑车到姥姥家,走的线路如图.已知去时与返回的速度比是4:5.
(1)小咏什么时候到达姥姥家?
(2)小咏在姥姥家玩了多长时间?
(3)如果10:50的时候小咏在离家300米处,小咏家与姥姥家相距多少米?
6、如图①,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥CA的延长线点E,由∠1+∠2=∠D+∠2=90°,得∠1=∠D,又∠ACB=∠AED=90°,AB=AD,得△ABC≌△DAE进而得到AC=DE,BC=AE, 我们把这个数学模型称为“K字”模型或“一线三等角”模型.
请应用上述“一线三等角”模型,解决下列问题:
(1)如图②,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC、DE,且BC⊥AH于点H,DE与直线AH交于点G,求证:点G是DE的中点.
(2)如图③,在平面直角坐标系中,点A为平面内任意一点,点B的坐标为(4,1),若△AOB是以OB为斜边的等腰直角三角形,请直接写出点A的坐标.
班级:________ 姓名:________
一、单选题(共 10 小题)
1、如图,,,点,,则点B的坐标是( )
A. B. C. D.
2、均匀的向一个容器内注水,在注水过程中,水面高度与时间的函数关系如图所示,则该容器是下列中的( )
A. B. C. D.
3、已知A、B两点的坐标分别是和,下列结论错误的是( )
A.点A在第二象限 B.点B在第一象限
C.线段平行于y轴 D.点A、B之间的距离为4
4、若点A(,)、点B(3,),且AB∥x轴,则AB的值为( )
A.2 B.3 C.4 D.5
5、在平面直角坐标系xoy中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,,点A2的伴随点为A3,,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(2,4),点A2020的坐标为( )
A.(-3,3) B.(-2,-2) C.(3,-1) D.(2,4)
6、如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为( )
A.(2,3) B.(0,3) C.(3,2) D.(2,2)
7、已知点,若直线轴,点P在x轴的负半轴上,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8、如图,直角坐标平面内,动点P按图中箭头所示方向依次运动,第1次从点运动到点,第2次运动到点,第3次运动到点,…,按这样的运动规律,动点P第2022次运动到点的坐标是( )
A. B. C. D.
9、当点A(x﹣1,3)到点B(﹣2,2y+5)的距离最短时,点P(x,y)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10、已知点关于原点的对称点在第四象限,则的取值范围在数轴上表示正确的是( )
A. B.
C. D.
二、填空题(共 10 小题)
1、若对于所有的实数,都有,则______.
2、若点P 关于原点的对称点Q在第三象限,那么m的取值范围是_______.
3、将一组数,,3,,,…..按下面的方式进行排列:
,,3,,;
,,,,;
.....
若的位置记为(1,4),的位置记为(2,3),则这组数中最大的有理数的位置记为_____.
4、如图,在平面直角坐标系中,点A,B,D的坐标为,,,点P从点B出发,沿﹣运动,速度为每秒1个单位长度,设运动时间为t秒;点Q以每秒2个单位长度的速度从点D出发,在DA间往返运动,(两个点同时出发,当点P到达点A停止时点Q也停止),在运动过程中,当时,点P的坐标为___________.
5、如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P61的坐标是_______.
6、如图所示的是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的关系图象.下列说法:①买2件时甲、乙两家售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买乙家的1件售价约为3元.其中正确的说法是__.
7、如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2022次变换后所得的A点坐标是___.
8、如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为______.
9、由图可知,在平面直角坐标系中,一块等腰直角三角板如图放置,其中,则点的坐标为___________;
10、如图,在平面直角坐标系中,以A(2,0),B(0,1)为顶点作等腰直角三角形ABC(其中∠ABC=90°,且点C落在第一象限),则点C关于y轴的对称点C'的坐标为______.
三、解答题(共 6 小题)
1、如图,是一个简单的平面示意图,已知OA=2km,OB=6km,OC=BD=4km,点E为OC的中点,回答下列问题:
(1)由图可知,高铁站在小明家南偏西65°方向6km处.请类似这种方法用方向与距离描述学校、博物馆相对于小明家的位置;
(2)图中到小明家距离相同的是哪些地方?
(3)若小强家在小明家北偏西60°方向2km处,请在图中标出小强家的位置.
2、在平面直角坐标系中,点从原点出发,沿轴正方向按折线不断向前运动,其移动路线如图所示.这时点,,,的坐标分别为,,,,,按照这个规律,解决下列问题:
(1)写出下列点的坐标: , , , ;
(2)点和点的位置分别在 , .(填轴上方、轴下方或轴上)
3、如图是小李骑自行车离家的距离s (km)与时间t (h) 之间的关系.
(1)在这个变化过程中自变量__________,因变量是__________,
(2)小李__________时到达离家最远的地方 此时离家________km;
(3)分别写出在1<t<2时和2<t<4时小李骑自行车的速度为______ km/h 和______km/h.
(4)小李______时与家相距20km.
4、如图,在平面直角坐标系中,已知三点,其中a、b满足关系式.
(1)求a、b、c的值;
(2)如果在第二象限内有一点,请用含m的式子表示四边形的面积;
(3)在(2)的条件下,是否存在点P,使四边形的面积与的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
5、小咏星期日上午8:00从家骑车到姥姥家,走的线路如图.已知去时与返回的速度比是4:5.
(1)小咏什么时候到达姥姥家?
(2)小咏在姥姥家玩了多长时间?
(3)如果10:50的时候小咏在离家300米处,小咏家与姥姥家相距多少米?
6、如图①,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥CA的延长线点E,由∠1+∠2=∠D+∠2=90°,得∠1=∠D,又∠ACB=∠AED=90°,AB=AD,得△ABC≌△DAE进而得到AC=DE,BC=AE, 我们把这个数学模型称为“K字”模型或“一线三等角”模型.
请应用上述“一线三等角”模型,解决下列问题:
(1)如图②,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC、DE,且BC⊥AH于点H,DE与直线AH交于点G,求证:点G是DE的中点.
(2)如图③,在平面直角坐标系中,点A为平面内任意一点,点B的坐标为(4,1),若△AOB是以OB为斜边的等腰直角三角形,请直接写出点A的坐标.
同课章节目录
