第7章平面图形的认识(二)单元测试(含答案)2022-2023学年苏科版数学七年级下册
文档属性
| 名称 | 第7章平面图形的认识(二)单元测试(含答案)2022-2023学年苏科版数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 445.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-06 14:24:37 | ||
图片预览

文档简介
第7章 平面图形的认识(二) 单元测试(5)
一、单选题(本大题共8小题24分)
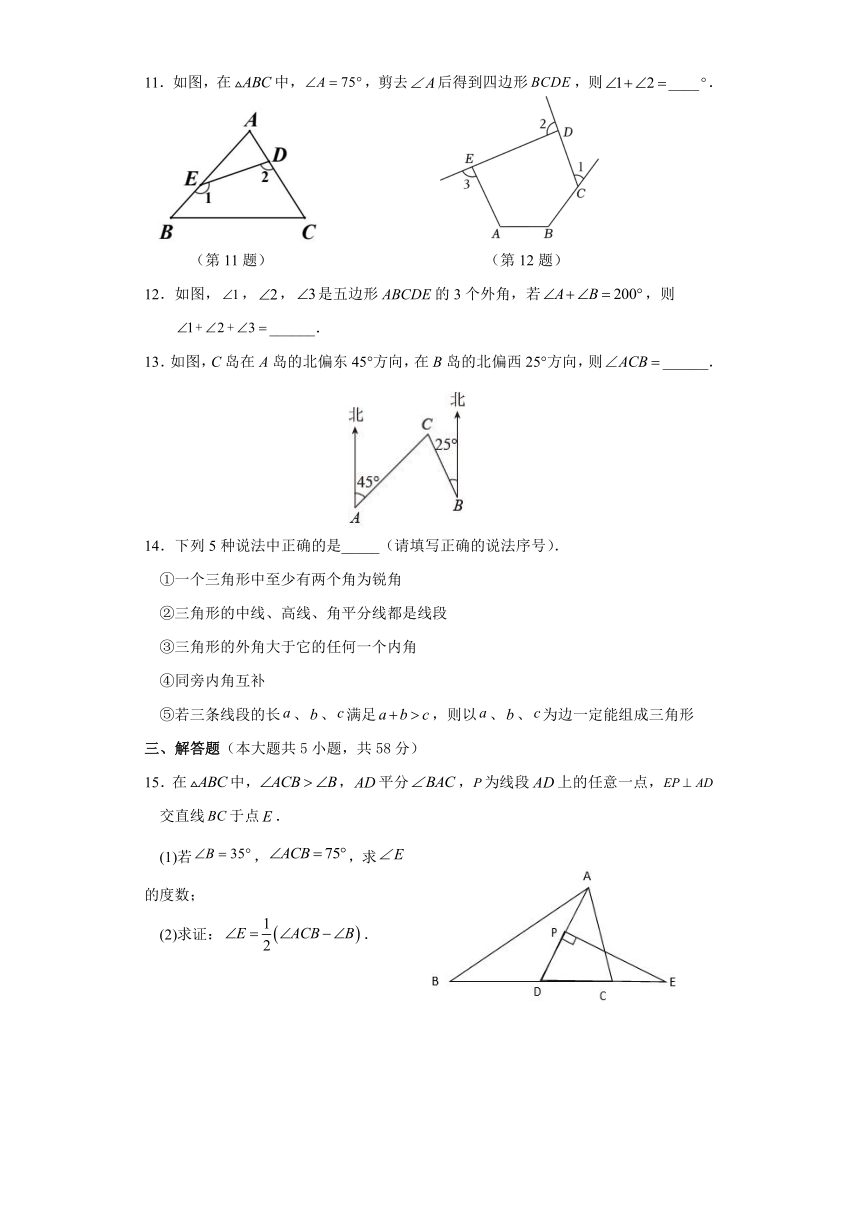
1.将一个含有角的直角三角板摆放在矩形上,如图所示,若,则( )
A. B. C. D.
(第1题) (第2题) (第3题)
2.五边形中,,、、分别是外角,则等于( )
A. B. C. D.
3.如图,下列判断:①与是同位角;②与是同旁内角;③与是内错角;④与是同位角.其中正确的是( )
A. B. C. D.
4.下列长度的三条线段,能构成三角形的是( )
A.3,10,5 B.4,8,4 C.5,13,12 D.2,7,4
5.用三根木棒做一个三角形,有两根6cm,8cm木棒,,可以选第三根木棒的长为( )
A.2cm B.6cm C.14cm D.16cm
6.在中,若,则此三角形是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等腰三角形
7.一个多边形的内角和是它外角和的2倍,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
8.如图所示,图中共有内错角( ).
A.2组 B.3组 C.4组 D.5组
(第8题) (第9题)
二、填空题(本大题共6小题18分)
9.如图,已知,则等于 ____.
10.在计算n边形内角和时,漏了一个内角,得到和为,这个角大小是____.
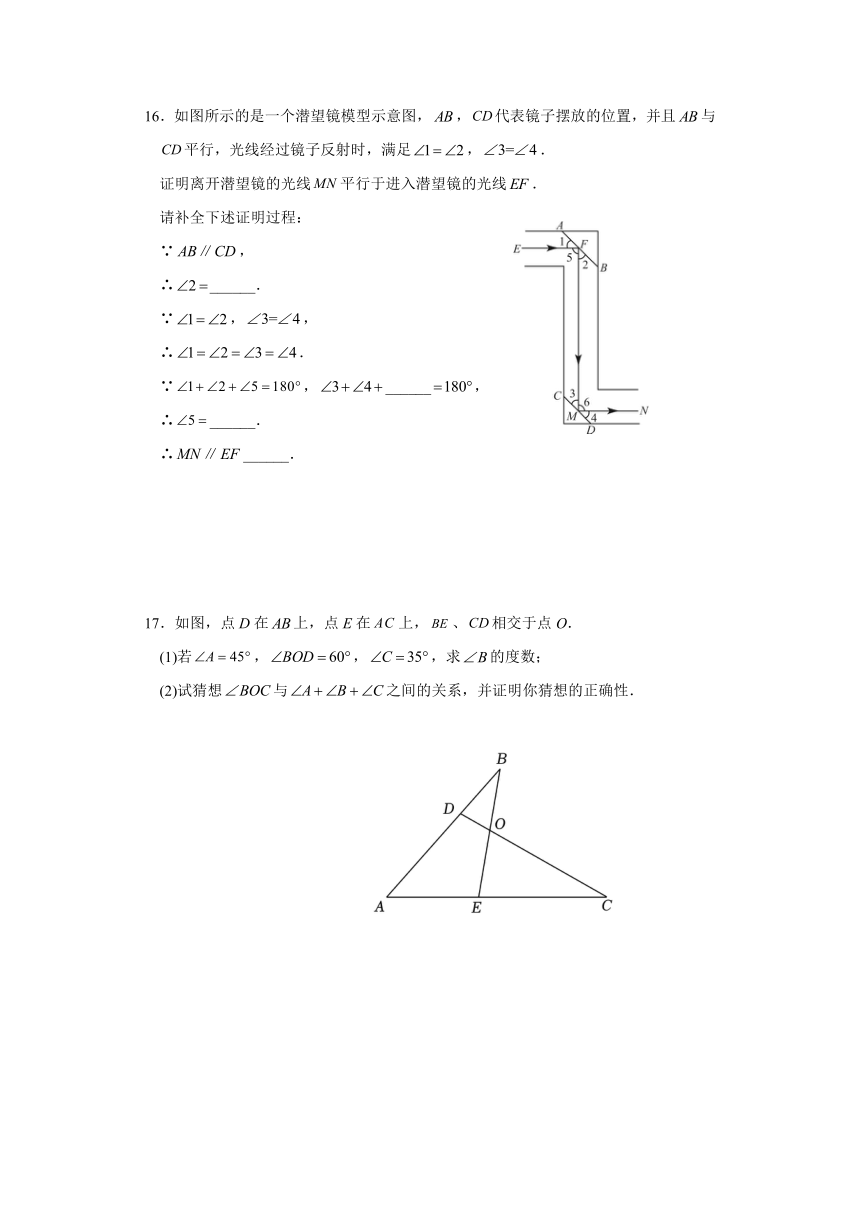
11.如图,在中,,剪去后得到四边形,则____.
(第11题) (第12题)
12.如图,,,是五边形ABCDE的3个外角,若,则______.
13.如图,C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,则______.
14.下列5种说法中正确的是_____(请填写正确的说法序号).
①一个三角形中至少有两个角为锐角
②三角形的中线、高线、角平分线都是线段
③三角形的外角大于它的任何一个内角
④同旁内角互补
⑤若三条线段的长、、满足,则以、、为边一定能组成三角形
三、解答题(本大题共5小题,共58分)
15.在中,,平分,为线段上的任意一点, 交直线于点.
(1)若,,求的度数;
(2)求证:.
16.如图所示的是一个潜望镜模型示意图,,代表镜子摆放的位置,并且与平行,光线经过镜子反射时,满足,.
证明离开潜望镜的光线平行于进入潜望镜的光线.
请补全下述证明过程:
∵,
∴______.
∵,,
∴.
∵,______,
∴______.
∴______.
17.如图,点D在上,点E在上,、相交于点O.
(1)若,,,求的度数;
(2)试猜想与之间的关系,并证明你猜想的正确性.
18.如图,与相交于,,与互补.
(1)说明的理由;
(2)若,,求的度数.
19.阅读下面内容,并解答问题.
在学行线的性质后,老师请学生们证明命题:两条平行线被第三条直线所截,一组同旁内角的平分线互相垂直.
小丽根据命题画出图形并写出如下的已知条件.
已知:如图1,,直线分别交,于点.的平分线与的平分线交于点G.求证:______.
(1)请补充要求证的结论,并写出证明过程;
(2)如图2,,直线分别交,于点点O在直线之间,且在直线右侧,的平分线与的平分线交于点P,求与满足的数量关系,并说明理由.
参考答案:
一、选择:1.D 2.B 3.A 4.C 5.B 6.B 7.C 8.B
二、填空:9. 10. 11.255 12. 13. 14.①②
三、解答:
15.(1)解:∵,,
∴,
∵平分,
∴,
∴,
又∵,
∴与互余,
∴;
(2)证明:∵平分,
∴,
∴
,
∵,
∴
16.解:∵, ∴.
∵,,∴.
∵,,
∴.
∴(内错角相等,两直线平行).
17.(1)∵,,
∴,
∵,
∴;
(2),理由如下:
∵是的外角,
∴,
∵是的外角,
∴,
∴.
18.(1)解:,,
,
∴,
,
,
∴;
(2)解:∵,,,
,
.
19.(1)解:结论:;
理由:,,
平分平分,
.
在中,,
,
.
(2)在图2中,过点O作,交于点N,过点P作,交于点M,
,
,
∴,
,
同理,
平分平分,
,
.
一、单选题(本大题共8小题24分)
1.将一个含有角的直角三角板摆放在矩形上,如图所示,若,则( )
A. B. C. D.
(第1题) (第2题) (第3题)
2.五边形中,,、、分别是外角,则等于( )
A. B. C. D.
3.如图,下列判断:①与是同位角;②与是同旁内角;③与是内错角;④与是同位角.其中正确的是( )
A. B. C. D.
4.下列长度的三条线段,能构成三角形的是( )
A.3,10,5 B.4,8,4 C.5,13,12 D.2,7,4
5.用三根木棒做一个三角形,有两根6cm,8cm木棒,,可以选第三根木棒的长为( )
A.2cm B.6cm C.14cm D.16cm
6.在中,若,则此三角形是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等腰三角形
7.一个多边形的内角和是它外角和的2倍,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
8.如图所示,图中共有内错角( ).
A.2组 B.3组 C.4组 D.5组
(第8题) (第9题)
二、填空题(本大题共6小题18分)
9.如图,已知,则等于 ____.
10.在计算n边形内角和时,漏了一个内角,得到和为,这个角大小是____.
11.如图,在中,,剪去后得到四边形,则____.
(第11题) (第12题)
12.如图,,,是五边形ABCDE的3个外角,若,则______.
13.如图,C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,则______.
14.下列5种说法中正确的是_____(请填写正确的说法序号).
①一个三角形中至少有两个角为锐角
②三角形的中线、高线、角平分线都是线段
③三角形的外角大于它的任何一个内角
④同旁内角互补
⑤若三条线段的长、、满足,则以、、为边一定能组成三角形
三、解答题(本大题共5小题,共58分)
15.在中,,平分,为线段上的任意一点, 交直线于点.
(1)若,,求的度数;
(2)求证:.
16.如图所示的是一个潜望镜模型示意图,,代表镜子摆放的位置,并且与平行,光线经过镜子反射时,满足,.
证明离开潜望镜的光线平行于进入潜望镜的光线.
请补全下述证明过程:
∵,
∴______.
∵,,
∴.
∵,______,
∴______.
∴______.
17.如图,点D在上,点E在上,、相交于点O.
(1)若,,,求的度数;
(2)试猜想与之间的关系,并证明你猜想的正确性.
18.如图,与相交于,,与互补.
(1)说明的理由;
(2)若,,求的度数.
19.阅读下面内容,并解答问题.
在学行线的性质后,老师请学生们证明命题:两条平行线被第三条直线所截,一组同旁内角的平分线互相垂直.
小丽根据命题画出图形并写出如下的已知条件.
已知:如图1,,直线分别交,于点.的平分线与的平分线交于点G.求证:______.
(1)请补充要求证的结论,并写出证明过程;
(2)如图2,,直线分别交,于点点O在直线之间,且在直线右侧,的平分线与的平分线交于点P,求与满足的数量关系,并说明理由.
参考答案:
一、选择:1.D 2.B 3.A 4.C 5.B 6.B 7.C 8.B
二、填空:9. 10. 11.255 12. 13. 14.①②
三、解答:
15.(1)解:∵,,
∴,
∵平分,
∴,
∴,
又∵,
∴与互余,
∴;
(2)证明:∵平分,
∴,
∴
,
∵,
∴
16.解:∵, ∴.
∵,,∴.
∵,,
∴.
∴(内错角相等,两直线平行).
17.(1)∵,,
∴,
∵,
∴;
(2),理由如下:
∵是的外角,
∴,
∵是的外角,
∴,
∴.
18.(1)解:,,
,
∴,
,
,
∴;
(2)解:∵,,,
,
.
19.(1)解:结论:;
理由:,,
平分平分,
.
在中,,
,
.
(2)在图2中,过点O作,交于点N,过点P作,交于点M,
,
,
∴,
,
同理,
平分平分,
,
.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
