广东省惠州市惠阳区学2022-2023学年七年级数学下学期开学考试测试卷(附答案解析)
文档属性
| 名称 | 广东省惠州市惠阳区学2022-2023学年七年级数学下学期开学考试测试卷(附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 200.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-05 12:40:54 | ||
图片预览



文档简介
广东省惠州市惠阳区2022-2023学年七年级数学下册开学考试测试卷(附答案)
一、单选题:共30分。
1.﹣5的倒数的相反数是( )
A.﹣5 B.5 C. D.
2.点P(x,y)的坐标满足xy>0,且x+y>0,则点P在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列运算一定正确的是( )
A.2a+3a=6a B.a2+a3=a5 C.a8÷a2=a6 D.(a3)4=a7
4.小明同学做了下面四道计算题:①(x2)3=x5;②(﹣x﹣y)2=x2﹣2xy+y2;③(x+y)(y﹣x)=y2﹣x2;④(x2y)3=x6y3,其中正确的个数是( )
A.4 B.3 C.2 D.1
5.如图,如果AB∥EF、EF∥CD,若∠1=50°,则∠2+∠3的和是( )
A.200° B.210° C.220° D.230°
6.如图,正方形ABCD的边长AB=8,E为平面内一动点,且AE=4,F为CD上一点,CF=2,连接EF,ED,则2EF+ED的最小值为( )
A.12 B.12 C.12 D.10
7.下列运算正确的是( )
A.4a+b=4ab B.a2+a3=a5
C.3a+2a=5a D.2a2b3﹣2a3b2=0
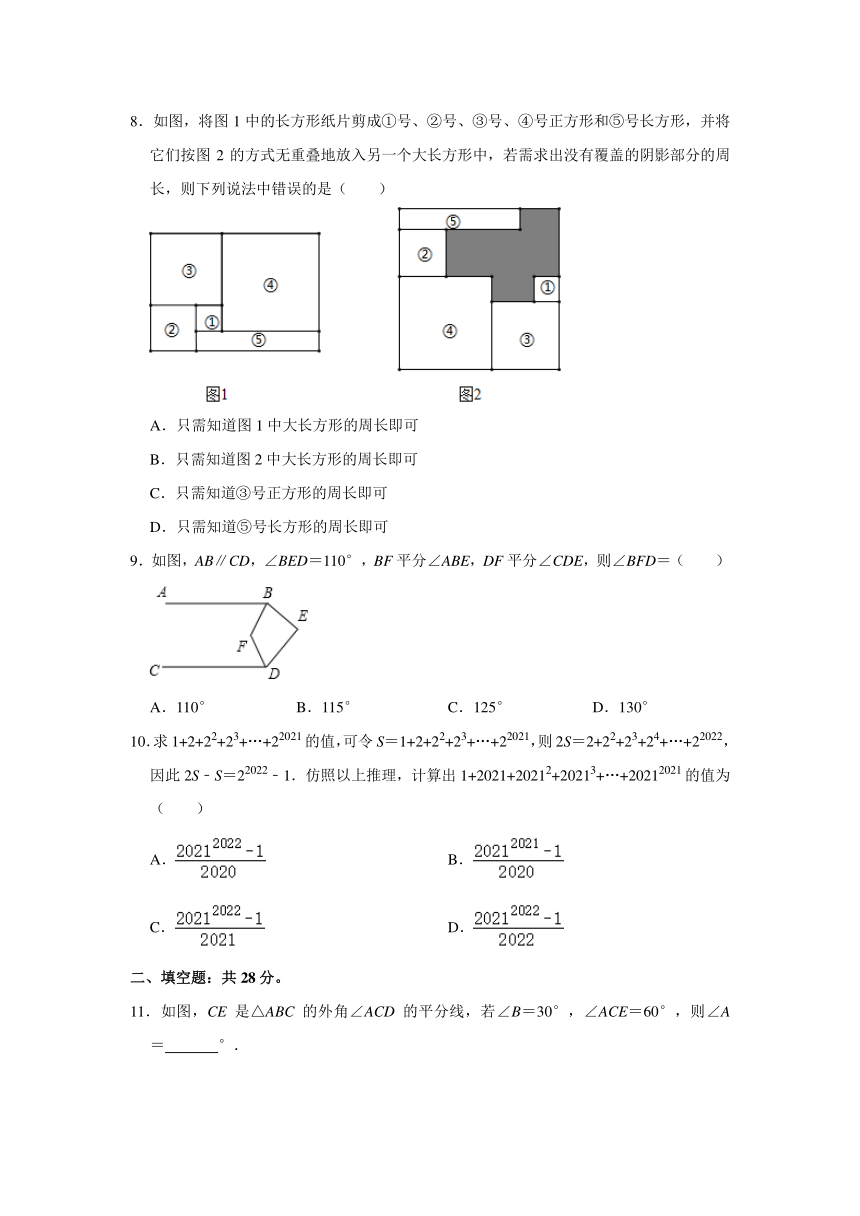
8.如图,将图1中的长方形纸片剪成①号、②号、③号、④号正方形和⑤号长方形,并将它们按图2的方式无重叠地放入另一个大长方形中,若需求出没有覆盖的阴影部分的周长,则下列说法中错误的是( )
A.只需知道图1中大长方形的周长即可
B.只需知道图2中大长方形的周长即可
C.只需知道③号正方形的周长即可
D.只需知道⑤号长方形的周长即可
9.如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=( )
A.110° B.115° C.125° D.130°
10.求1+2+22+23+…+22021的值,可令S=1+2+22+23+…+22021,则2S=2+22+23+24+…+22022,因此2S﹣S=22022﹣1.仿照以上推理,计算出1+2021+20212+20213+…+20212021的值为( )
A. B.
C. D.
二、填空题:共28分。
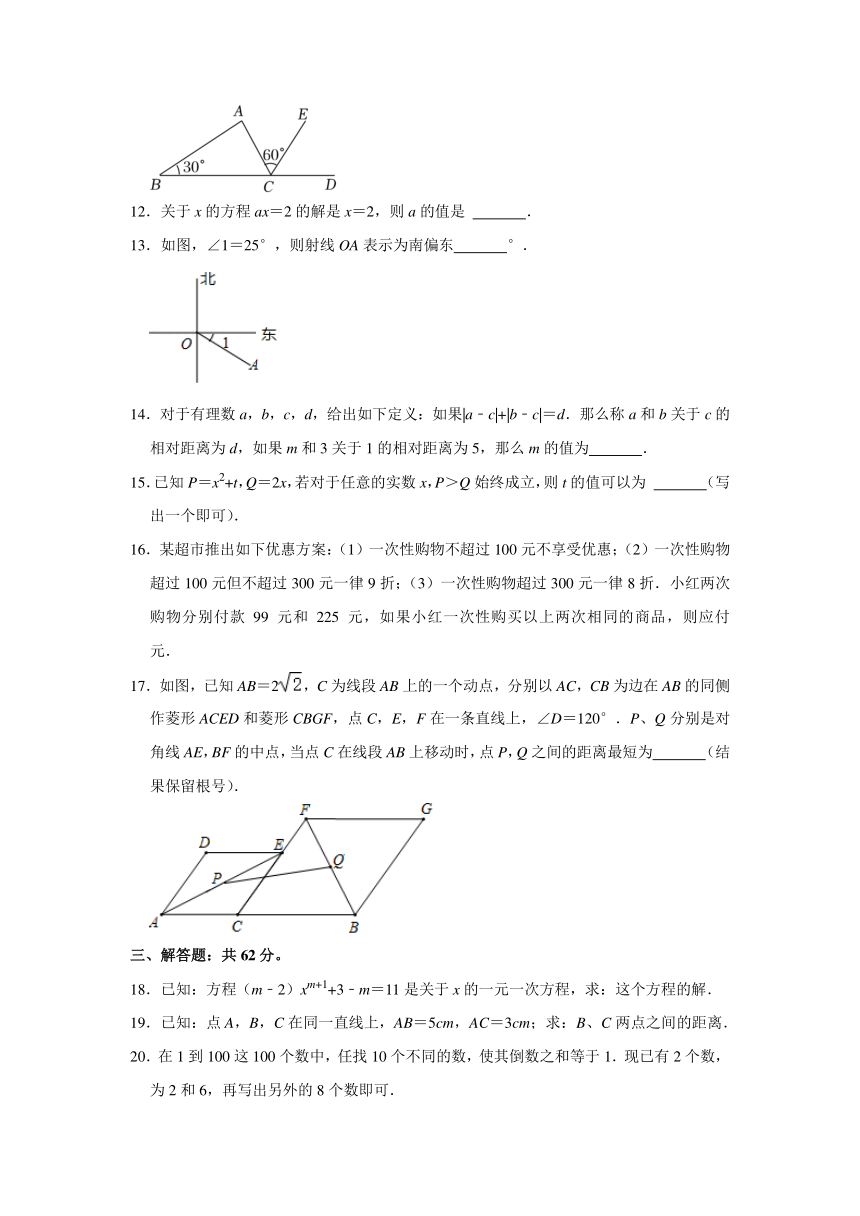
11.如图,CE是△ABC的外角∠ACD的平分线,若∠B=30°,∠ACE=60°,则∠A= °.
12.关于x的方程ax=2的解是x=2,则a的值是 .
13.如图,∠1=25°,则射线OA表示为南偏东 °.
14.对于有理数a,b,c,d,给出如下定义:如果|a﹣c|+|b﹣c|=d.那么称a和b关于c的相对距离为d,如果m和3关于1的相对距离为5,那么m的值为 .
15.已知P=x2+t,Q=2x,若对于任意的实数x,P>Q始终成立,则t的值可以为 (写出一个即可).
16.某超市推出如下优惠方案:(1)一次性购物不超过100元不享受优惠;(2)一次性购物超过100元但不超过300元一律9折;(3)一次性购物超过300元一律8折.小红两次购物分别付款99元和225元,如果小红一次性购买以上两次相同的商品,则应付 元.
17.如图,已知AB=2,C为线段AB上的一个动点,分别以AC,CB为边在AB的同侧作菱形ACED和菱形CBGF,点C,E,F在一条直线上,∠D=120°.P、Q分别是对角线AE,BF的中点,当点C在线段AB上移动时,点P,Q之间的距离最短为 (结果保留根号).
三、解答题:共62分。
18.已知:方程(m﹣2)xm+1+3﹣m=11是关于x的一元一次方程,求:这个方程的解.
19.已知:点A,B,C在同一直线上,AB=5cm,AC=3cm;求:B、C两点之间的距离.
20.在1到100这100个数中,任找10个不同的数,使其倒数之和等于1.现已有2个数,为2和6,再写出另外的8个数即可.
21.有一个正方体,在它的各个面上分别标上数字1、2、3、4、5、6.小明、小刚、小红三人从不同的角度去观察此正方体,观察结果如图所示,问这个正方体各个面上的数字对面各是什么数字?
22.一天,小红与小莉利用温差测量山峰的高度,小红在山顶测得温度是﹣1℃,小莉此时在山脚测得温度是5℃.已知该地区高度每增加100米,气温大约降低0.8℃,这个山峰的高度大约是多少米?
23.点A,B,C在直线l上,若AB=4cm,BC=3cm,点O是线段AC的中点,那么线段OB的长是多少?
小明同学根据下述图形对这个题目进行了求解:
∵A,B,C三点顺次在直线l上,
∴AC=AB+BC,
∵AB=4cm,BC=3cm,
∴AC=7cm,
又∵点O为线段AC的中点,
∴AO=AC=×7=3.5cm,
∴OB=AB﹣AO=4﹣3.5=0.5cm.
小明考虑得全面吗?如果不全面,请补全解题过程,如果全面,请说明理由.
24.某礼品制造厂接了一批玩具熊的订单,按计划天数生产,若每天生产20个玩具熊,则最终比订单少生产100个;若每天生产23个玩具熊,则最终比订单多生产20个.原计划几天完成订单?
25.如图,在△ABC中,AD⊥BC于D,AE平分∠DAC,∠BAC=80°,∠B=60°,求∠DAE的度数.
参考答案
一、单选题:共30分。
1.解:﹣5的倒数的相反数是.
故选:D.
2.解:∵xy>0,
∴xy为同号即为同正或同负,
∵x+y>0,
∴x>0,y>0,
∴点P(x,y)在第一象限.
故选:A.
3.解:A、2a+3a=5a,故此选项错误,不符合题意;
B、a2与a3无法合并,故此选项错误,不符合题意;
C、a8÷a2=a6,故此选项正确,符合题意;
D、(a3)4=a12,故此选项错误,不符合题意.
故选:C.
4.解:①(x2)3=x6,原计算错误;
②(﹣x﹣y)2=x2+2xy+y2,原计算错误;
③(x+y)(y﹣x)=y2﹣x2,原计算正确;
④(x2y)3=x6y3,原计算错误.
故正确的有1个.
故选:D.
5.解:∵AB∥EF,
∴∠2+∠BOE=180°,
∴∠BOE=180°﹣∠2,同理可得∠COF=180°﹣∠3,
∵O在EF上,
∴∠BOE+∠1+∠COF=180°,
∴180°﹣∠2+∠1+180°﹣∠3=180°,
∴∠2+∠3=180°+∠1=180°+50°=230°,
故选:D.
6.解:如图,当点E运动到点E′时,
在AD边上取AH=2,
∵AE′=AE=4,
∴AE′:AH=2:1,
∵AD=8,
∴AD:AE′=8:4=2:1,
∴AD:AE′=AE′:AH,
∵∠DAE′=∠E′AH,
∴△DAE′∽△E′AH,
∴DE′:E′H=2:1,
即DE′=2E′H,
∵2EF+ED=2E′F+E′D=2E′F+2E′H=2HF,
∴2EF+ED的最小值即为2HF的值,
∵DH=AD﹣AH=6,
DF=DC﹣CF=6,
在Rt△DHF中,根据勾股定理,得
HF==6,
∴2HF=12.
故选:B.
7.解:A.4a与b不是同类项,所以不能合并,故本选项不合题意;
B.a2与a3不是同类项,所以不能合并,故本选项不合题意;
C.3a+2a=5a,故本选项符合题意;
D.2a2b3与﹣2a3b2不是同类项,所以不能合并,故本选项不合题意;
故选:C.
8.解:设①号正方形的边长为x,②号正方形的边长为y,
则③号正方形的边长为x+y,④号正方形的边长为2x+y,
⑤号长方形的长为3x+y,宽为y﹣x,
∴AB=2x+y+x+y﹣y=3x+y,
BD=y﹣x+y+2x+y﹣x﹣y=2y,
根据题意得:没有覆盖的阴影部分的周长=2 (AB+BD)
=2(3x+y+2y)
=6(x+y).
∵图1中大长方形的周长=2(3x+y+y+x+y+y)=8(x+y);
图2中大长方形的周长=2(2x+y+x+y+y﹣x+y+2x+y)=8x+10y;
⑤号长方形的周长=2(y﹣x+3x+y)=4(x+y);
∴选项A,C,D说法正确,不符合题意,
选项B说法错误,符合题意.
故选:B.
9.解:过点E作EM∥AB,过点F作FN∥AB,
∵AB∥CD,
∴EM∥AB∥CD∥FN,
∴∠ABE+∠BEM=180°,∠CDE+∠DEM=180°,
∴∠ABE+∠BED+∠CDE=360°,
∵∠BED=110°,
∴∠ABE+∠CDE=250°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠ABF=∠ABE,∠CDF=∠CDE,
∴∠ABF+∠CDF=(∠ABE+∠CDE)=125°,
∵∠DFN=∠CDF,∠BFN=∠ABF,
∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°.
故选:C.
10.解:记S=1+2021+20212+20213+…+20212021,
则2021S=2021+20212+20213+…+20212021+20212022,
∴2021S﹣S=20212022﹣1,
故S=.
故选:A.
二、填空题:共28分。
11.解:∵CE平分∠ACD,∠ACE=60°,
∴∠ACD=2∠ACE=120°,
∵∠ACD是△ABC的外角,∠B=30°,
∴∠ACD=∠A+∠B,
∴∠A=∠ACD﹣∠B=90°.
故答案为:90.
12.解:把x=2代入方程得:2a=2,
解得:a=1.
故答案是:1.
13.解:标记∠2,如图所示.
∵∠1=25°,∠1+∠2=90°,
∴∠2=65°.
∴射线OA表示南偏东65°.
故答案是:65.
14.解:由题意得|m﹣1|+|3﹣1|=5,
即|m﹣1|=3,
∴m﹣1=3或m﹣1=﹣3,
解得m=4或﹣2,
故答案为4或﹣2.
15.解:∵P=x2+t,Q=2x,
∴若对于任意的实数x,P>Q始终成立,必须x2+t>2x,
即:x2﹣2x+t>0,
∵x2﹣2x+t=(x﹣1)2+t﹣1,
又(x﹣1)2≥0,
∴当t﹣1>0时,x2﹣2x+t>0永远成立,即P>Q始终成立.
∴t>1.
故答案为:2(答案不唯一).
16.解:小红一次性购物付款99元,据条件(1)、(2)知她有可能享受九折优惠,则实际购物款为:99÷0.9=110(元),
也可能实际就是99元,没有优惠,则实际购物款为99元;
另一次购物付款225元,只有一种可能,是购物超过100元但不超过300元按九折计算,则实际购物款为=250(元).
250+110=360(元),或250+99=349(元),
即小红两次购物总价值为360元,349元,
若一次性购买这些商品应付款为:
则360×0.8=288(元),或349×0.8=279.2(元).
故答案为:288或279.2.
17.解:连接PC、CQ.
∵四边形ACED,四边形CBGF是菱形,∠D=120°,
∴∠ACE=120°,∠FCB=60°,
∵P,Q分别是对角线AE,BF的中点,
∴∠ECP=∠ACE,∠FCQ=∠BCF,
∴∠PCQ=90°,
设AC=2a,则BC=2﹣2a,PC=a,CQ=BC=().
∴PQ===.
∴当a=时,点P,Q之间的距离最短,最短距离是.
解法二:连接CD、CG、DG,构造中位线解决,当DG与AD或BG垂直时,取最值.
故答案为:.
三、解答题:共62分。
18.解:∵方程(m﹣2)xm+1+3﹣m=11是关于x的一元一次方程,
∴,
解得:m=0,
∴原方程为﹣2x+3=11,
解得:x=﹣4,
∴这个方程的解为x=﹣4.
19.解:当C在线段AB的反向延长线上时,
BC=AB+AC=5+3=8cm,
当C在线段AB上时,
BC=AB﹣AC=5﹣3=2cm,
综上所述:B、C两点之间的距离是8cm或2cm.
20.解:∵1=1﹣+﹣+﹣+…+﹣+
=(1﹣)+(﹣)+(﹣)+…+(﹣)+
=+,
∴这10个数可以是:2、6、10、12、20、30、42、56、72、90(答案不唯一).
21.解:从3个小立方体上的数可知,
与写有数字1的面相邻的面上数字是2,3,4,6,
所以数字1面对数字5面,
同理,立方体面上数字3对6.
故立方体面上数字2对4.
22.设这个山峰的高度大约是x米,
根据题意得:5﹣×0.8=﹣1,
解得:x=750.
即这个山峰大约是750米;
23.解:不全面,
当点C在点B的左侧时,如图:
∵A,B,C三点顺次在直线l上,
∴AC=AB﹣BC,
∵AB=4cm,BC=3cm,
∴AC=1cm,
又∵点O为线段AC的中点,
∴AO=AC=×1=0.5cm,
∴OB=AB﹣AO=4﹣0.5=3.5cm,
∴线段OB的长是0.5cm或3.5cm.
24.解:设原计划用x天完成,
20x+100=23x﹣20,
3x=120,
解得:x=40,
答:原计划用40天完成.
25.解:∵∠BAC=80°,∠B=60°,
∴∠C=180°﹣∠BAC﹣∠B=180°﹣80°﹣60°=40°,
∵AD⊥BC,
∴∠DAC=90°﹣∠C=90°﹣40°=50°,
∵AE平分∠DAC,
∴∠DAE=∠DAC=×50°=25°.
一、单选题:共30分。
1.﹣5的倒数的相反数是( )
A.﹣5 B.5 C. D.
2.点P(x,y)的坐标满足xy>0,且x+y>0,则点P在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列运算一定正确的是( )
A.2a+3a=6a B.a2+a3=a5 C.a8÷a2=a6 D.(a3)4=a7
4.小明同学做了下面四道计算题:①(x2)3=x5;②(﹣x﹣y)2=x2﹣2xy+y2;③(x+y)(y﹣x)=y2﹣x2;④(x2y)3=x6y3,其中正确的个数是( )
A.4 B.3 C.2 D.1
5.如图,如果AB∥EF、EF∥CD,若∠1=50°,则∠2+∠3的和是( )
A.200° B.210° C.220° D.230°
6.如图,正方形ABCD的边长AB=8,E为平面内一动点,且AE=4,F为CD上一点,CF=2,连接EF,ED,则2EF+ED的最小值为( )
A.12 B.12 C.12 D.10
7.下列运算正确的是( )
A.4a+b=4ab B.a2+a3=a5
C.3a+2a=5a D.2a2b3﹣2a3b2=0
8.如图,将图1中的长方形纸片剪成①号、②号、③号、④号正方形和⑤号长方形,并将它们按图2的方式无重叠地放入另一个大长方形中,若需求出没有覆盖的阴影部分的周长,则下列说法中错误的是( )
A.只需知道图1中大长方形的周长即可
B.只需知道图2中大长方形的周长即可
C.只需知道③号正方形的周长即可
D.只需知道⑤号长方形的周长即可
9.如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=( )
A.110° B.115° C.125° D.130°
10.求1+2+22+23+…+22021的值,可令S=1+2+22+23+…+22021,则2S=2+22+23+24+…+22022,因此2S﹣S=22022﹣1.仿照以上推理,计算出1+2021+20212+20213+…+20212021的值为( )
A. B.
C. D.
二、填空题:共28分。
11.如图,CE是△ABC的外角∠ACD的平分线,若∠B=30°,∠ACE=60°,则∠A= °.
12.关于x的方程ax=2的解是x=2,则a的值是 .
13.如图,∠1=25°,则射线OA表示为南偏东 °.
14.对于有理数a,b,c,d,给出如下定义:如果|a﹣c|+|b﹣c|=d.那么称a和b关于c的相对距离为d,如果m和3关于1的相对距离为5,那么m的值为 .
15.已知P=x2+t,Q=2x,若对于任意的实数x,P>Q始终成立,则t的值可以为 (写出一个即可).
16.某超市推出如下优惠方案:(1)一次性购物不超过100元不享受优惠;(2)一次性购物超过100元但不超过300元一律9折;(3)一次性购物超过300元一律8折.小红两次购物分别付款99元和225元,如果小红一次性购买以上两次相同的商品,则应付 元.
17.如图,已知AB=2,C为线段AB上的一个动点,分别以AC,CB为边在AB的同侧作菱形ACED和菱形CBGF,点C,E,F在一条直线上,∠D=120°.P、Q分别是对角线AE,BF的中点,当点C在线段AB上移动时,点P,Q之间的距离最短为 (结果保留根号).
三、解答题:共62分。
18.已知:方程(m﹣2)xm+1+3﹣m=11是关于x的一元一次方程,求:这个方程的解.
19.已知:点A,B,C在同一直线上,AB=5cm,AC=3cm;求:B、C两点之间的距离.
20.在1到100这100个数中,任找10个不同的数,使其倒数之和等于1.现已有2个数,为2和6,再写出另外的8个数即可.
21.有一个正方体,在它的各个面上分别标上数字1、2、3、4、5、6.小明、小刚、小红三人从不同的角度去观察此正方体,观察结果如图所示,问这个正方体各个面上的数字对面各是什么数字?
22.一天,小红与小莉利用温差测量山峰的高度,小红在山顶测得温度是﹣1℃,小莉此时在山脚测得温度是5℃.已知该地区高度每增加100米,气温大约降低0.8℃,这个山峰的高度大约是多少米?
23.点A,B,C在直线l上,若AB=4cm,BC=3cm,点O是线段AC的中点,那么线段OB的长是多少?
小明同学根据下述图形对这个题目进行了求解:
∵A,B,C三点顺次在直线l上,
∴AC=AB+BC,
∵AB=4cm,BC=3cm,
∴AC=7cm,
又∵点O为线段AC的中点,
∴AO=AC=×7=3.5cm,
∴OB=AB﹣AO=4﹣3.5=0.5cm.
小明考虑得全面吗?如果不全面,请补全解题过程,如果全面,请说明理由.
24.某礼品制造厂接了一批玩具熊的订单,按计划天数生产,若每天生产20个玩具熊,则最终比订单少生产100个;若每天生产23个玩具熊,则最终比订单多生产20个.原计划几天完成订单?
25.如图,在△ABC中,AD⊥BC于D,AE平分∠DAC,∠BAC=80°,∠B=60°,求∠DAE的度数.
参考答案
一、单选题:共30分。
1.解:﹣5的倒数的相反数是.
故选:D.
2.解:∵xy>0,
∴xy为同号即为同正或同负,
∵x+y>0,
∴x>0,y>0,
∴点P(x,y)在第一象限.
故选:A.
3.解:A、2a+3a=5a,故此选项错误,不符合题意;
B、a2与a3无法合并,故此选项错误,不符合题意;
C、a8÷a2=a6,故此选项正确,符合题意;
D、(a3)4=a12,故此选项错误,不符合题意.
故选:C.
4.解:①(x2)3=x6,原计算错误;
②(﹣x﹣y)2=x2+2xy+y2,原计算错误;
③(x+y)(y﹣x)=y2﹣x2,原计算正确;
④(x2y)3=x6y3,原计算错误.
故正确的有1个.
故选:D.
5.解:∵AB∥EF,
∴∠2+∠BOE=180°,
∴∠BOE=180°﹣∠2,同理可得∠COF=180°﹣∠3,
∵O在EF上,
∴∠BOE+∠1+∠COF=180°,
∴180°﹣∠2+∠1+180°﹣∠3=180°,
∴∠2+∠3=180°+∠1=180°+50°=230°,
故选:D.
6.解:如图,当点E运动到点E′时,
在AD边上取AH=2,
∵AE′=AE=4,
∴AE′:AH=2:1,
∵AD=8,
∴AD:AE′=8:4=2:1,
∴AD:AE′=AE′:AH,
∵∠DAE′=∠E′AH,
∴△DAE′∽△E′AH,
∴DE′:E′H=2:1,
即DE′=2E′H,
∵2EF+ED=2E′F+E′D=2E′F+2E′H=2HF,
∴2EF+ED的最小值即为2HF的值,
∵DH=AD﹣AH=6,
DF=DC﹣CF=6,
在Rt△DHF中,根据勾股定理,得
HF==6,
∴2HF=12.
故选:B.
7.解:A.4a与b不是同类项,所以不能合并,故本选项不合题意;
B.a2与a3不是同类项,所以不能合并,故本选项不合题意;
C.3a+2a=5a,故本选项符合题意;
D.2a2b3与﹣2a3b2不是同类项,所以不能合并,故本选项不合题意;
故选:C.
8.解:设①号正方形的边长为x,②号正方形的边长为y,
则③号正方形的边长为x+y,④号正方形的边长为2x+y,
⑤号长方形的长为3x+y,宽为y﹣x,
∴AB=2x+y+x+y﹣y=3x+y,
BD=y﹣x+y+2x+y﹣x﹣y=2y,
根据题意得:没有覆盖的阴影部分的周长=2 (AB+BD)
=2(3x+y+2y)
=6(x+y).
∵图1中大长方形的周长=2(3x+y+y+x+y+y)=8(x+y);
图2中大长方形的周长=2(2x+y+x+y+y﹣x+y+2x+y)=8x+10y;
⑤号长方形的周长=2(y﹣x+3x+y)=4(x+y);
∴选项A,C,D说法正确,不符合题意,
选项B说法错误,符合题意.
故选:B.
9.解:过点E作EM∥AB,过点F作FN∥AB,
∵AB∥CD,
∴EM∥AB∥CD∥FN,
∴∠ABE+∠BEM=180°,∠CDE+∠DEM=180°,
∴∠ABE+∠BED+∠CDE=360°,
∵∠BED=110°,
∴∠ABE+∠CDE=250°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠ABF=∠ABE,∠CDF=∠CDE,
∴∠ABF+∠CDF=(∠ABE+∠CDE)=125°,
∵∠DFN=∠CDF,∠BFN=∠ABF,
∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°.
故选:C.
10.解:记S=1+2021+20212+20213+…+20212021,
则2021S=2021+20212+20213+…+20212021+20212022,
∴2021S﹣S=20212022﹣1,
故S=.
故选:A.
二、填空题:共28分。
11.解:∵CE平分∠ACD,∠ACE=60°,
∴∠ACD=2∠ACE=120°,
∵∠ACD是△ABC的外角,∠B=30°,
∴∠ACD=∠A+∠B,
∴∠A=∠ACD﹣∠B=90°.
故答案为:90.
12.解:把x=2代入方程得:2a=2,
解得:a=1.
故答案是:1.
13.解:标记∠2,如图所示.
∵∠1=25°,∠1+∠2=90°,
∴∠2=65°.
∴射线OA表示南偏东65°.
故答案是:65.
14.解:由题意得|m﹣1|+|3﹣1|=5,
即|m﹣1|=3,
∴m﹣1=3或m﹣1=﹣3,
解得m=4或﹣2,
故答案为4或﹣2.
15.解:∵P=x2+t,Q=2x,
∴若对于任意的实数x,P>Q始终成立,必须x2+t>2x,
即:x2﹣2x+t>0,
∵x2﹣2x+t=(x﹣1)2+t﹣1,
又(x﹣1)2≥0,
∴当t﹣1>0时,x2﹣2x+t>0永远成立,即P>Q始终成立.
∴t>1.
故答案为:2(答案不唯一).
16.解:小红一次性购物付款99元,据条件(1)、(2)知她有可能享受九折优惠,则实际购物款为:99÷0.9=110(元),
也可能实际就是99元,没有优惠,则实际购物款为99元;
另一次购物付款225元,只有一种可能,是购物超过100元但不超过300元按九折计算,则实际购物款为=250(元).
250+110=360(元),或250+99=349(元),
即小红两次购物总价值为360元,349元,
若一次性购买这些商品应付款为:
则360×0.8=288(元),或349×0.8=279.2(元).
故答案为:288或279.2.
17.解:连接PC、CQ.
∵四边形ACED,四边形CBGF是菱形,∠D=120°,
∴∠ACE=120°,∠FCB=60°,
∵P,Q分别是对角线AE,BF的中点,
∴∠ECP=∠ACE,∠FCQ=∠BCF,
∴∠PCQ=90°,
设AC=2a,则BC=2﹣2a,PC=a,CQ=BC=().
∴PQ===.
∴当a=时,点P,Q之间的距离最短,最短距离是.
解法二:连接CD、CG、DG,构造中位线解决,当DG与AD或BG垂直时,取最值.
故答案为:.
三、解答题:共62分。
18.解:∵方程(m﹣2)xm+1+3﹣m=11是关于x的一元一次方程,
∴,
解得:m=0,
∴原方程为﹣2x+3=11,
解得:x=﹣4,
∴这个方程的解为x=﹣4.
19.解:当C在线段AB的反向延长线上时,
BC=AB+AC=5+3=8cm,
当C在线段AB上时,
BC=AB﹣AC=5﹣3=2cm,
综上所述:B、C两点之间的距离是8cm或2cm.
20.解:∵1=1﹣+﹣+﹣+…+﹣+
=(1﹣)+(﹣)+(﹣)+…+(﹣)+
=+,
∴这10个数可以是:2、6、10、12、20、30、42、56、72、90(答案不唯一).
21.解:从3个小立方体上的数可知,
与写有数字1的面相邻的面上数字是2,3,4,6,
所以数字1面对数字5面,
同理,立方体面上数字3对6.
故立方体面上数字2对4.
22.设这个山峰的高度大约是x米,
根据题意得:5﹣×0.8=﹣1,
解得:x=750.
即这个山峰大约是750米;
23.解:不全面,
当点C在点B的左侧时,如图:
∵A,B,C三点顺次在直线l上,
∴AC=AB﹣BC,
∵AB=4cm,BC=3cm,
∴AC=1cm,
又∵点O为线段AC的中点,
∴AO=AC=×1=0.5cm,
∴OB=AB﹣AO=4﹣0.5=3.5cm,
∴线段OB的长是0.5cm或3.5cm.
24.解:设原计划用x天完成,
20x+100=23x﹣20,
3x=120,
解得:x=40,
答:原计划用40天完成.
25.解:∵∠BAC=80°,∠B=60°,
∴∠C=180°﹣∠BAC﹣∠B=180°﹣80°﹣60°=40°,
∵AD⊥BC,
∴∠DAC=90°﹣∠C=90°﹣40°=50°,
∵AE平分∠DAC,
∴∠DAE=∠DAC=×50°=25°.
同课章节目录
