人教版数学八年级下册17.2勾股定理的逆定理 练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册17.2勾股定理的逆定理 练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 355.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-06 00:00:00 | ||
图片预览




文档简介
17.2勾股定理的逆定理
一、选择题(共11题)
以下列各组数为边长,能构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
在 中,,则 是
A.等腰三角形 B.钝角三角形
C.直角三角形 D.等腰直角三角形
的三边长分别为 ,,.下列条件:① ﹔② ;③ ;④ .其中能判断 是直角三角形的个数有
A. 个 B. 个 C. 个 D. 个
满足下列条件的三角形中,不是直角三角形的是
A.三内角的度数之比为 B.三内角的度数之比为
C.三边长之比为 D.三边长的平方之比为
若 的三边分别为 ,, ,则 的面积是
A. B. C. D.
已知 ,, 是 的三边,且满足 ,则 一定是
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为 和 .按照输油中心 到三条支路的距离相等来连接管道,则 到三条支路的管道总长(计算时视管道为线,中心 为点)是
A. B. C. D.
如图,点 是正 内的一点,,,,则 的度数是
A. B. C. D.
如图是一个棱长为 的正方体的展开图,点 ,, 是展开后小正方形的顶点,连接 ,,则 的大小是
A. B. C. D.
在 中,,, 分别是 ,, 的对边,若 ,则这个三角形一定是
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.钝角三角形
甲、乙两艘客轮沿不同方向同时离开港口 ,航行的速度都是 ,甲客轮 到达点 ,乙客轮用 到达 点,若 , 两点的直线距离为 ,甲客轮沿北偏东 的方向航行,则乙客轮的航行方向可能是
A.南偏西 B.北偏西 C.南偏东 D.南偏西
二、填空题(共6题)
理解互逆定理的概念:
一般地,如果一个定理的 经过证明是正确的,那么它也是一个 ,称这两个定理互为 .
已知 的三边长为 ,,,满足 ,,,则此三角形是 三角形.
观察下列勾股数组:① ,,;② ,,;③ ,,;④ ,,;.若 ,, 是其中的一组勾股数,则根据你发现的规律, .
某住宅小区有一块草坪如图所示,已知 米, 米, 米, 米,且 ,这块草坪的面积是 平方米.
如图,在边长为 的小正方形组成的网格中, 的三个顶点均在格点上.请按要求完成下列各题:
()判断 是 三角形;
()计算 的面积 .
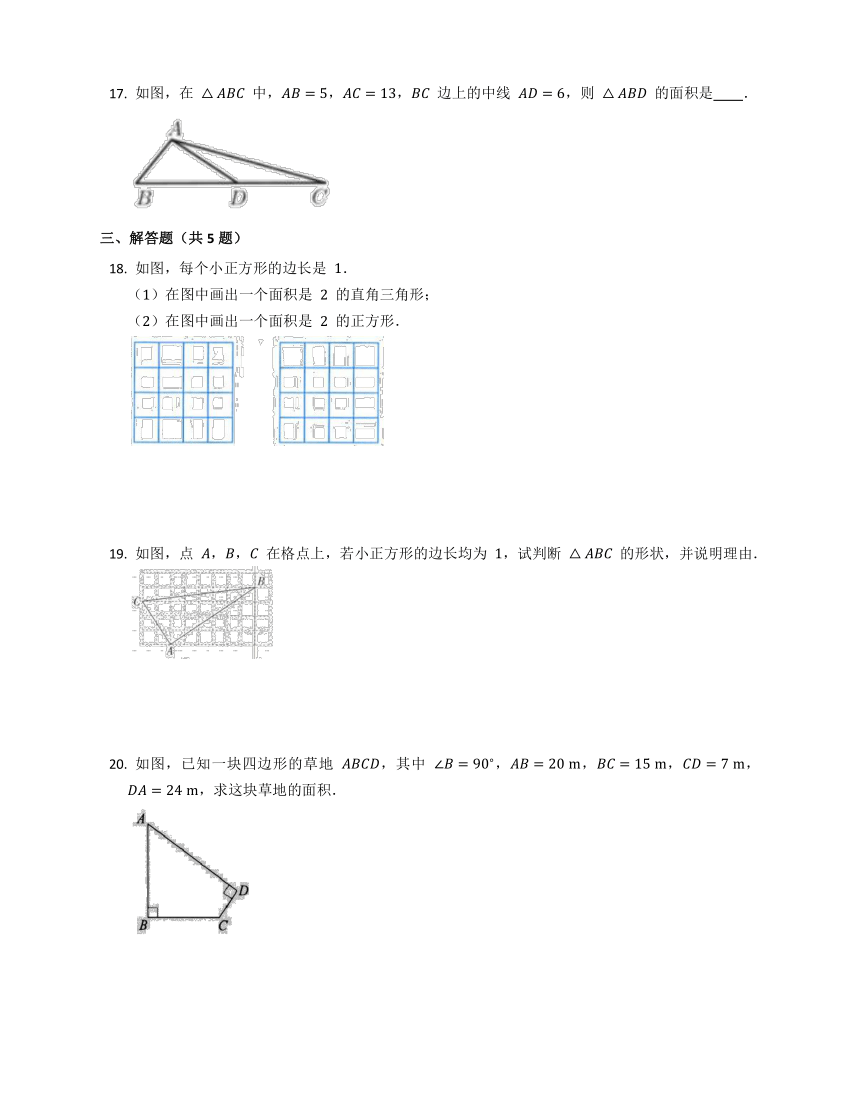
如图,在 中,,, 边上的中线 ,则 的面积是 .
三、解答题(共5题)
如图,每个小正方形的边长是 .
()在图中画出一个面积是 的直角三角形;
()在图中画出一个面积是 的正方形.
如图,点 ,, 在格点上,若小正方形的边长均为 ,试判断 的形状,并说明理由.
如图,已知一块四边形的草地 ,其中 ,,,,,求这块草地的面积.
如图,在 中,边 , 的垂直平分线分别交 于点 、点 .
(1) 若 ,则 周长是 .
(2) 若 ,,,则 面积是 .
(3) 若 ,求 的度数是多少.
阅读:
小明同学在某材料中看到如下问题及部分证明.
如图①,已知在 和 中,,,,,,求证:.
证明:延长 到 ,使 ,连接 ,延长 到 ,使 ,连接 ,
在 和 中,
(已作),
(对顶角相等),
(已知),
,
(全等三角形的对应边相等),
同理可证,,
未完待续
(1) 请你补全这个证明.
(2) 应用:如图②,在 中, 是 边上的中线,若 ,,则 长的范围是 .
(3) 拓展:如图③,在 中, 是 边上的中线,若 ,,,则 的面积是 .
答案
一、选择题(共11题)
1. 【答案】C
2. 【答案】D
3. 【答案】C
【解析】①由 ,可知:,是直角三角形.
②由 ,可得 ,是直角三角形.
③由 ,可知不是直角三角形.
④由 ,根据勾股定理逆定理可知是直角三角形.
4. 【答案】B
5. 【答案】A
【解析】 的三边分别为 ,,,且
是直角三角形,两直角边是 ,,
则 .
6. 【答案】C
【解析】 ,,
,
,
即 ,
为直角三角形.
7. 【答案】C
8. 【答案】D
【解析】 为等边三角形,
,,
把 绕点 顺时针旋转 得到 ,
如图,连接 ,
,,,
为等边三角形,
,,
在 中,
,,,
,
为直角三角形,,
.
9. 【答案】C
【解析】连接 .
根据勾股定理可以得到:,,
,即 ,
是等腰直角三角形.
.
10. 【答案】C
【解析】 ,
则 ,,,
则 ,,
.
为等腰直角三角形.
11. 【答案】C
【解析】如图:
甲乙两艘客轮同时离开港口,航行的速度都是每分钟 ,甲客轮用 分钟到达点 ,乙客轮用 分钟到达点 ,
甲客轮走了 ,乙客轮走了 ,
, 两点的直线距离为 ,
,
,
甲客轮沿着北偏东 的方向航行,
乙客轮的航行方向可能是南偏东 .
故选C.
二、填空题(共6题)
12. 【答案】逆命题;定理;逆定理
13. 【答案】直角
【解析】 ,,,
,
又 ,
,
此三角形是直角三角形.
14. 【答案】
15. 【答案】
【解析】连接 ,如图.
,
,
米, 米,
米,
米, 米,
为直角三角形,
16. 【答案】直角;
【解析】(),,,
,
,
是直角三角形,
故答案为:直角;
(),,
,,
,
故答案为:.
17. 【答案】
【解析】延长 到点 ,使 ,连接 ,
是 边上的中线,
,
在 和 中,
,
,,
,,,
,
,
,
即 为直角三角形.
的面积 .
三、解答题(共5题)
18. 【答案】略
19. 【答案】 是直角三角形.
理由:由题意,可知 ,,.
.
是直角三角形.
20. 【答案】如图,连接 ,如图所示.
,,,
.
,,,
,
是直角三角形,且 ,
,
,
.
21. 【答案】
(1)
(2)
(3) ,
,
边 , 的垂直平分线分别交 于点 、点 .
,,
,
.
【解析】
(1) , 的垂直平分线分别交 于点 ,点 ,
,,
,
的周长是 .
(2) ,,,
,,,
,
,
是以 为斜边的直角三角形,
的面积是 .
22. 【答案】
(1) ,
,即 ,
在 和 中,
,
.
(2)
(3)
【解析】
(2) 延长 至 ,使 ,连接 ,,
由()可知,,
,
.
(3) 延长 至 ,使 ,连接 ,
同理可证,,,
,
是 ,
.
一、选择题(共11题)
以下列各组数为边长,能构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
在 中,,则 是
A.等腰三角形 B.钝角三角形
C.直角三角形 D.等腰直角三角形
的三边长分别为 ,,.下列条件:① ﹔② ;③ ;④ .其中能判断 是直角三角形的个数有
A. 个 B. 个 C. 个 D. 个
满足下列条件的三角形中,不是直角三角形的是
A.三内角的度数之比为 B.三内角的度数之比为
C.三边长之比为 D.三边长的平方之比为
若 的三边分别为 ,, ,则 的面积是
A. B. C. D.
已知 ,, 是 的三边,且满足 ,则 一定是
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为 和 .按照输油中心 到三条支路的距离相等来连接管道,则 到三条支路的管道总长(计算时视管道为线,中心 为点)是
A. B. C. D.
如图,点 是正 内的一点,,,,则 的度数是
A. B. C. D.
如图是一个棱长为 的正方体的展开图,点 ,, 是展开后小正方形的顶点,连接 ,,则 的大小是
A. B. C. D.
在 中,,, 分别是 ,, 的对边,若 ,则这个三角形一定是
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.钝角三角形
甲、乙两艘客轮沿不同方向同时离开港口 ,航行的速度都是 ,甲客轮 到达点 ,乙客轮用 到达 点,若 , 两点的直线距离为 ,甲客轮沿北偏东 的方向航行,则乙客轮的航行方向可能是
A.南偏西 B.北偏西 C.南偏东 D.南偏西
二、填空题(共6题)
理解互逆定理的概念:
一般地,如果一个定理的 经过证明是正确的,那么它也是一个 ,称这两个定理互为 .
已知 的三边长为 ,,,满足 ,,,则此三角形是 三角形.
观察下列勾股数组:① ,,;② ,,;③ ,,;④ ,,;.若 ,, 是其中的一组勾股数,则根据你发现的规律, .
某住宅小区有一块草坪如图所示,已知 米, 米, 米, 米,且 ,这块草坪的面积是 平方米.
如图,在边长为 的小正方形组成的网格中, 的三个顶点均在格点上.请按要求完成下列各题:
()判断 是 三角形;
()计算 的面积 .
如图,在 中,,, 边上的中线 ,则 的面积是 .
三、解答题(共5题)
如图,每个小正方形的边长是 .
()在图中画出一个面积是 的直角三角形;
()在图中画出一个面积是 的正方形.
如图,点 ,, 在格点上,若小正方形的边长均为 ,试判断 的形状,并说明理由.
如图,已知一块四边形的草地 ,其中 ,,,,,求这块草地的面积.
如图,在 中,边 , 的垂直平分线分别交 于点 、点 .
(1) 若 ,则 周长是 .
(2) 若 ,,,则 面积是 .
(3) 若 ,求 的度数是多少.
阅读:
小明同学在某材料中看到如下问题及部分证明.
如图①,已知在 和 中,,,,,,求证:.
证明:延长 到 ,使 ,连接 ,延长 到 ,使 ,连接 ,
在 和 中,
(已作),
(对顶角相等),
(已知),
,
(全等三角形的对应边相等),
同理可证,,
未完待续
(1) 请你补全这个证明.
(2) 应用:如图②,在 中, 是 边上的中线,若 ,,则 长的范围是 .
(3) 拓展:如图③,在 中, 是 边上的中线,若 ,,,则 的面积是 .
答案
一、选择题(共11题)
1. 【答案】C
2. 【答案】D
3. 【答案】C
【解析】①由 ,可知:,是直角三角形.
②由 ,可得 ,是直角三角形.
③由 ,可知不是直角三角形.
④由 ,根据勾股定理逆定理可知是直角三角形.
4. 【答案】B
5. 【答案】A
【解析】 的三边分别为 ,,,且
是直角三角形,两直角边是 ,,
则 .
6. 【答案】C
【解析】 ,,
,
,
即 ,
为直角三角形.
7. 【答案】C
8. 【答案】D
【解析】 为等边三角形,
,,
把 绕点 顺时针旋转 得到 ,
如图,连接 ,
,,,
为等边三角形,
,,
在 中,
,,,
,
为直角三角形,,
.
9. 【答案】C
【解析】连接 .
根据勾股定理可以得到:,,
,即 ,
是等腰直角三角形.
.
10. 【答案】C
【解析】 ,
则 ,,,
则 ,,
.
为等腰直角三角形.
11. 【答案】C
【解析】如图:
甲乙两艘客轮同时离开港口,航行的速度都是每分钟 ,甲客轮用 分钟到达点 ,乙客轮用 分钟到达点 ,
甲客轮走了 ,乙客轮走了 ,
, 两点的直线距离为 ,
,
,
甲客轮沿着北偏东 的方向航行,
乙客轮的航行方向可能是南偏东 .
故选C.
二、填空题(共6题)
12. 【答案】逆命题;定理;逆定理
13. 【答案】直角
【解析】 ,,,
,
又 ,
,
此三角形是直角三角形.
14. 【答案】
15. 【答案】
【解析】连接 ,如图.
,
,
米, 米,
米,
米, 米,
为直角三角形,
16. 【答案】直角;
【解析】(),,,
,
,
是直角三角形,
故答案为:直角;
(),,
,,
,
故答案为:.
17. 【答案】
【解析】延长 到点 ,使 ,连接 ,
是 边上的中线,
,
在 和 中,
,
,,
,,,
,
,
,
即 为直角三角形.
的面积 .
三、解答题(共5题)
18. 【答案】略
19. 【答案】 是直角三角形.
理由:由题意,可知 ,,.
.
是直角三角形.
20. 【答案】如图,连接 ,如图所示.
,,,
.
,,,
,
是直角三角形,且 ,
,
,
.
21. 【答案】
(1)
(2)
(3) ,
,
边 , 的垂直平分线分别交 于点 、点 .
,,
,
.
【解析】
(1) , 的垂直平分线分别交 于点 ,点 ,
,,
,
的周长是 .
(2) ,,,
,,,
,
,
是以 为斜边的直角三角形,
的面积是 .
22. 【答案】
(1) ,
,即 ,
在 和 中,
,
.
(2)
(3)
【解析】
(2) 延长 至 ,使 ,连接 ,,
由()可知,,
,
.
(3) 延长 至 ,使 ,连接 ,
同理可证,,,
,
是 ,
.
