人教版数学八年级下册20.1数据的集中趋势 同步练(含解析)
文档属性
| 名称 | 人教版数学八年级下册20.1数据的集中趋势 同步练(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 925.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-06 00:00:00 | ||
图片预览


文档简介
20.1数据的集中趋势
一、选择题(共12题)
已知小华上学期语文、数学、英语三科平均分为 分,他记得语文得了 分,英语得了 分,但他把数学成绩忘记了,你能告诉他应该是以下哪个分数吗?
A. B. C. D.
某单位要招聘 名英语翻译,张明参加招聘考试的成绩如表所示:若把听、说、读、写的成绩按 计算平均成绩,则张明的平均成绩为
A. B. C. D.
某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
该店主决定本周进货时,增加了一些 码的衬衫,影响该店主决策的统计量是
A.众数 B.方差 C.平均数 D.中位数
某射击小组有 人,教练根据他们某次射击命中环数的数据绘制成如图的统计图,则这组数据的众数和极差分别是
A. , B. , C. , D. ,
某校在体育健康测试中,有 名男生“引体向上”的成绩(单位:次)分别是:,,,,,,,,这组数据的中位数和众数分别是
A. , B. , C. , D. ,
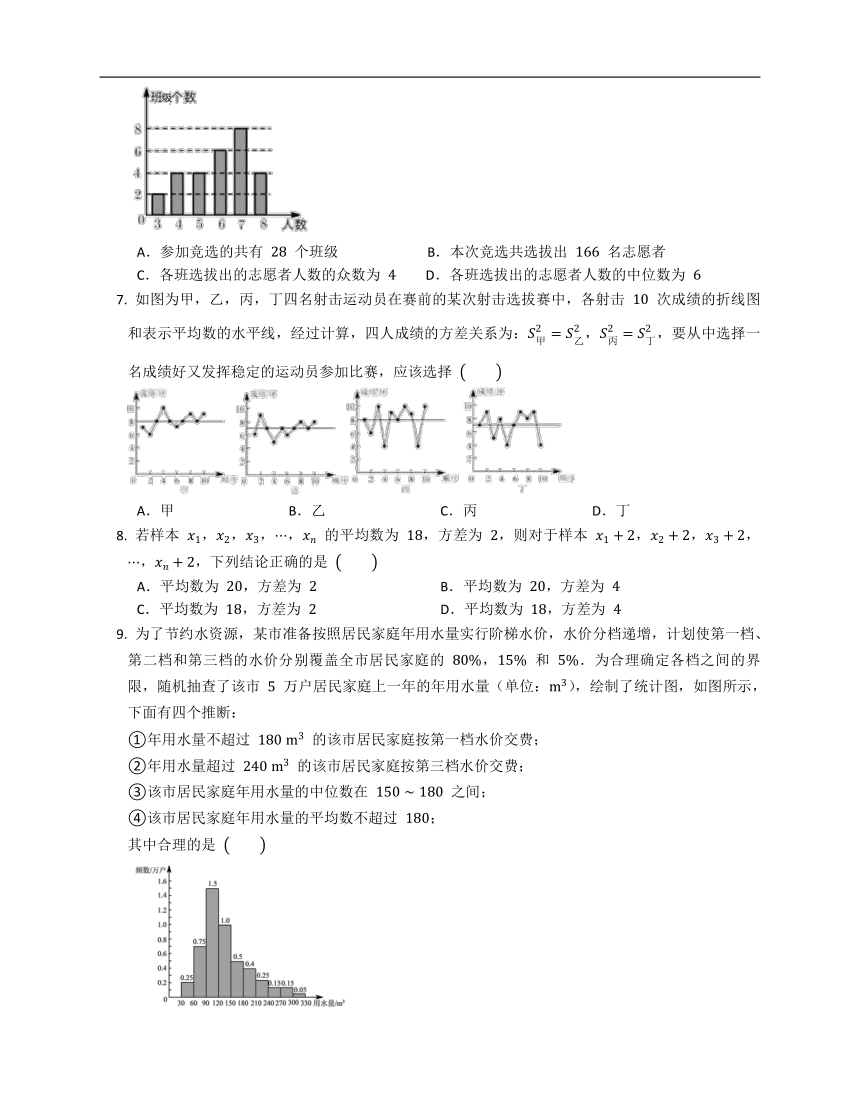
第七届世界军人运动会将于 年 月 日至 日在武汉举行.光谷某中学开展了“助力军动会”志愿者招募活动,同学们踊跃报名参与竞选.经选拔,最终每个班级都有同学光荣晋升为本次军运会志愿者.下面的条形统计图描述了这些班级选拔出的志愿者人数的情况;下列说法错误的是
A.参加竞选的共有 个班级 B.本次竞选共选拔出 名志愿者
C.各班选拔出的志愿者人数的众数为 D.各班选拔出的志愿者人数的中位数为
如图为甲,乙,丙,丁四名射击运动员在赛前的某次射击选拔赛中,各射击 次成绩的折线图和表示平均数的水平线,经过计算,四人成绩的方差关系为:,,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择
A.甲 B.乙 C.丙 D.丁
若样本 ,,,, 的平均数为 ,方差为 ,则对于样本 ,,,,,下列结论正确的是
A.平均数为 ,方差为 B.平均数为 ,方差为
C.平均数为 ,方差为 D.平均数为 ,方差为
为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的 , 和 .为合理确定各档之间的界限,随机抽查了该市 万户居民家庭上一年的年用水量(单位:),绘制了统计图,如图所示,下面有四个推断:
①年用水量不超过 的该市居民家庭按第一档水价交费;
②年用水量超过 的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在 之间;
④该市居民家庭年用水量的平均数不超过 ;
其中合理的是
A.①③ B.①④ C.②③ D.②④
为了解某校 名初三学生的睡眠时间,从中抽取 名学生进行调查,在这个问题中,下列说法正确的是
A. 名学生是总体 B. 是众数
C. 名学生是抽取的一个样本 D. 是样本的容量
某校共有 名学生,为了解本学期学生参加公益劳动的情况,收集了他们参加公益劳动时间(单位:)等数据,以下是根据数据绘制的统计图表的一部分:
下面有四个推断:
①这 名学生参加公益劳动时间的平均数一定在 之间;
②这 名学生参加公益劳动时间的中位数在 之间;
③这 名学生中,初中生参加公益劳动时间的中位数一定在 之间;
④这 名学生中,高中生参加公益劳动时间的中位数可能在 之间.
所有合理推断的序号是
A.①③ B.②④ C.①②③ D.①②③④
某电脑公司销售部为定制下个月的销售计划,对 名销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这 名销售员本月销售量的平均数、中位数、众数分别是
A. ,, B. ,, C. ,, D. ,,
二、填空题(共5题)
回顾所学,完善本课的知识结构图.
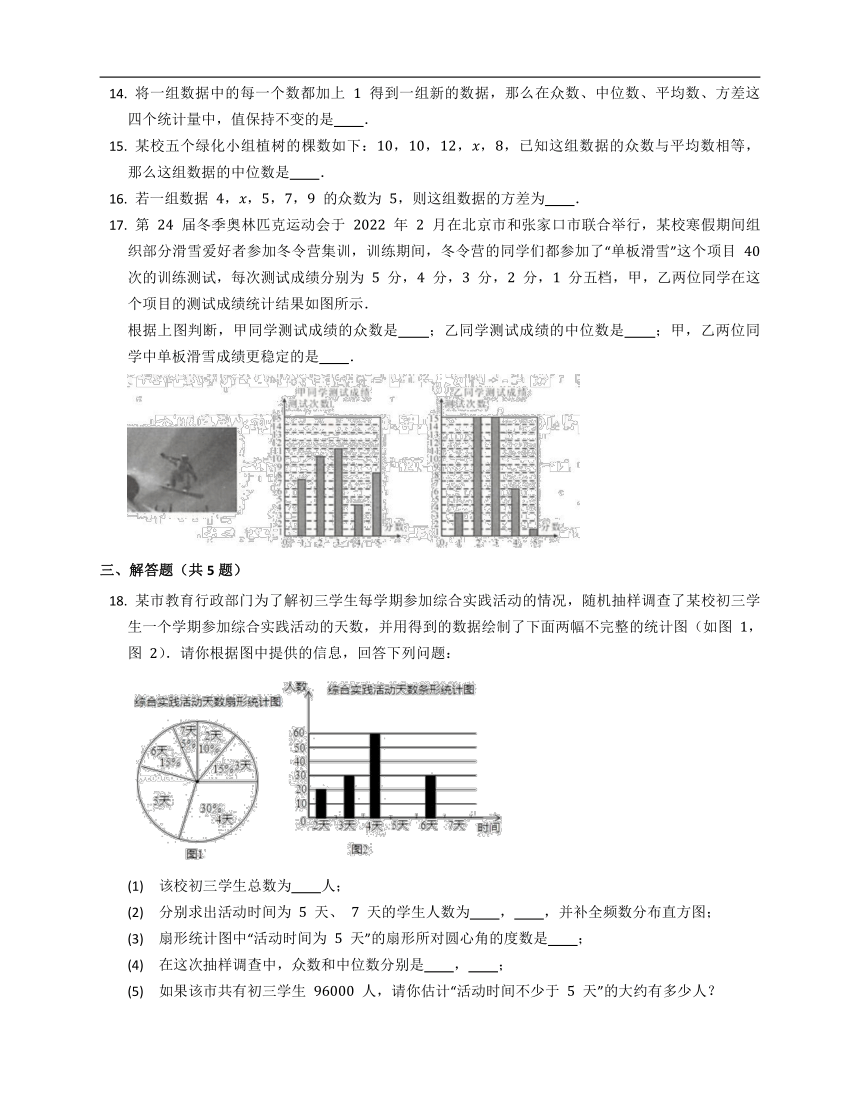
将一组数据中的每一个数都加上 得到一组新的数据,那么在众数、中位数、平均数、方差这四个统计量中,值保持不变的是 .
某校五个绿化小组植树的棵数如下:,,,,,已知这组数据的众数与平均数相等,那么这组数据的中位数是 .
若一组数据 ,,,, 的众数为 ,则这组数据的方差为 .
第 届冬季奥林匹克运动会于 年 月在北京市和张家口市联合举行,某校寒假期间组织部分滑雪爱好者参加冬令营集训,训练期间,冬令营的同学们都参加了“单板滑雪”这个项目 次的训练测试,每次测试成绩分别为 分, 分, 分, 分, 分五档,甲,乙两位同学在这个项目的测试成绩统计结果如图所示.
根据上图判断,甲同学测试成绩的众数是 ;乙同学测试成绩的中位数是 ;甲,乙两位同学中单板滑雪成绩更稳定的是 .
三、解答题(共5题)
某市教育行政部门为了解初三学生每学期参加综合实践活动的情况,随机抽样调查了某校初三学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图 ,图 ).请你根据图中提供的信息,回答下列问题:
(1) 该校初三学生总数为 人;
(2) 分别求出活动时间为 天、 天的学生人数为 , ,并补全频数分布直方图;
(3) 扇形统计图中“活动时间为 天”的扇形所对圆心角的度数是 ;
(4) 在这次抽样调查中,众数和中位数分别是 , ;
(5) 如果该市共有初三学生 人,请你估计“活动时间不少于 天”的大约有多少人?
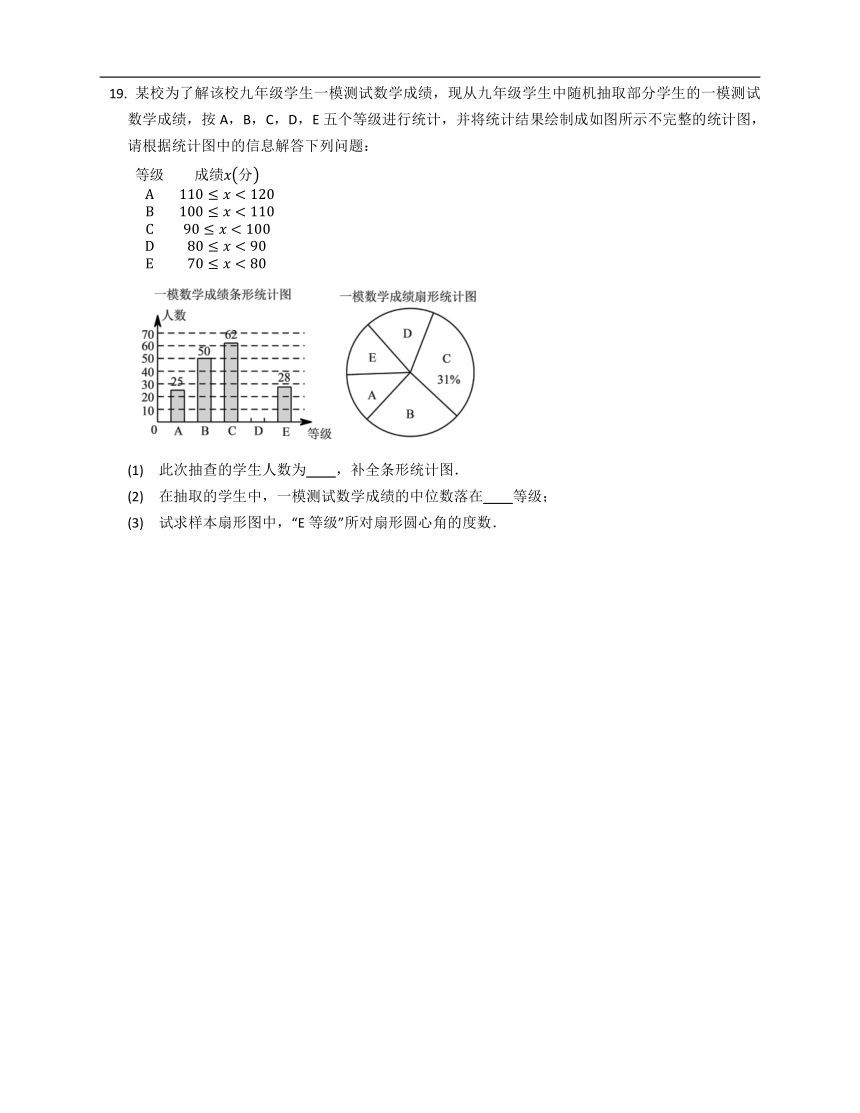
某校为了解该校九年级学生一模测试数学成绩,现从九年级学生中随机抽取部分学生的一模测试数学成绩,按A,B,C,D,E五个等级进行统计,并将统计结果绘制成如图所示不完整的统计图,请根据统计图中的信息解答下列问题:
(1) 此次抽查的学生人数为 ,补全条形统计图.
(2) 在抽取的学生中,一模测试数学成绩的中位数落在 等级;
(3) 试求样本扇形图中,“E等级”所对扇形圆心角的度数.
动手做一做.
每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某校为确保学生安全,开展了“远离溺水·珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用 表示,共分成四组:A.,B.,C.,D.),下面给出了部分信息:
七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
八年级10名学生的竞赛成绩在C组中的数据是:94,90,94
七、八年级抽取的学生竞赛成绩统计表
根据以上信息,解答下列问题:
(1) (1)直接写出上述图表中 ,, 的值;
(2) (2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3) (3)该校七、八年级共720人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀 的学生人数是多少?
我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出 名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的 名选手的决赛成绩如图所示.
(1) 根据图示计算出 ,, 的值;
(2) 结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3) 计算初中代表队决赛成绩的方差 ,并判断哪一个代表队选手成绩较为稳定.
为了防控新冠疫情,某地区积极推广疫苗接种工作,卫生防疫部门对该地区八周以来的相关数据进行收集整理,绘制得到如下图表:
该地区每周接种疫苗人数统计表
根据统计表中的数据,建立以周次为横坐标,接种人数为纵坐标的平面直角坐标系,并根据以上统计表中的数据描出对应的点,发现从第 周开始这些点大致分布在一条直线附近,现过其中两点 , 作一条直线(如图所示,该直线的函数表达式为 ),那么这条直线可近似反映该地区接种人数的变化趋势.
请根据以上信息,解答下列问题:
(1) 这八周中每周接种人数的平均数为 万;该地区的总人口约为 万;
(2) 若从第 周开始,每周的接种人数仍符合上述变化趋势.
①估计第 周的接种人数为 万;
②专家表示:疫苗接种率至少达 ,才能实现全民免疫.那么,从推广疫苗接种工作开始,最早到第几周,该地区可达到实现全民免疫的标准?
(3) 实际上,受疫苗供应等客观因素影响,从第 周开始,接种人数将会逐周减少 万,为了尽快提高接种率,一旦周接种人数低于 万时,卫生防疫部门将会采取措施,使得之后每周的接种人数一直维持在 万.如果 ,那么该地区的建议接种人群最早将于第几周全部完成接种?
答案
一、选择题(共12题)
1. 【答案】A
2. 【答案】C
3. 【答案】A
【解析】 码衬衫出现次数最多,
影响店主决策的统计量是众数.
4. 【答案】D
【解析】由条形统计图可知 出现的次数最多,则众数是 (环);
这组数据的最大值是 ,最小值是 ,则极差是 .
5. 【答案】C
【解析】原数据按由小到大排列为:,,,,,,,,
所以这组数据的中位数 ,众数为 .
故答案选C.
6. 【答案】C
7. 【答案】A
8. 【答案】A
【解析】样本 ,,,,,对于样本 ,,,, 来说,
每个数据均在原来的基础上增加了 ,根据平均数、方差的变化规律得:
平均数较前增加 ,而方差不变,即:平均数为 ,方差为 .
9. 【答案】B
【解析】提示:年用水量不超过 的占 .①中推理合理;
年用水量超过 的占 .②中推理不合理;
中位数在 之间;
年用水量的平均数约为 .
10. 【答案】D
11. 【答案】C
【解析】思路分析:通过频数分布表及统计图得到数据信息,再根据中位数与平均数的定义求解即可.
①这 名学生参加公益劳动时间的平均数为 ,一定在 之间,故①正确;
②由统计表类别栏计算可得,各时间段人数分别为 ,,,,,则中位数在 之间,故②正确.
③由统计表计算可得,初中学段栏中 的时间段的人数在 之间,当人数为 时,中位数在 之间;当人数为 时,中位数在 之间,故③正确.
④由统计表计算可得,高中学段各时间段人数分别为 ,,,,,当 时间段的人数为 时,中位数在 之间,当 时间段的人数为 时,中位数在 之间,故④错误.
故选:C.
12. 【答案】C
二、填空题(共5题)
13. 【答案】频数分布直方图;平均水平;波动程度;分布;频数
14. 【答案】方差
【解析】将一组数据中的每一个数都加上 得到一组新的数据,那么这组数据的波动幅度保持不变,即方差不变,而平均数和众数、中位数均改变.
故答案为:方差.
15. 【答案】
【解析】可知 ,,,, 的众数与平均数都是 ,
故 ,解得:,
将数据排列后得:,,,,,故中位数为 .
16. 【答案】
【解析】 数据 ,,,, 的众数为 ,
,
,
.
17. 【答案】 ; ;乙
三、解答题(共5题)
18. 【答案】
(1)
(2) ;
补全频数分布直方图如图所示:
(3)
(4) ;
(5) (人).
答:该市初三学生 人中“活动时间不少于 天”的大约有 人.
【解析】
(1) ,
故答案为:.
(2) 人,
人,
故答案为:,.
(3) .
故答案为:.
(4) 综合实践活动时间为 天的出现次数最多,是 次,因此众数是 天,
将综合实践时间从小到大排列后处在第 , 位的都是 天,因此中位数是 天,
故答案为:,.
19. 【答案】
(1) 人
补图略.
(2) C
(3) .
20. 【答案】
(1) (1),
∵八年级10名学生的竞赛成绩的中位数是第5和第6个数据的平均数,
∴ ;
∵在七年级10名学生的竞赛成绩中99出现的次数最多,
∴ ;
(2) (2)八年级学生掌握防溺水安全知识较好,理由:虽然七、八年级的平均分均为92分,但八年级的中位数和众数均高于七年级.
(3) (3)参加此次竞赛活动成绩优秀 的学生人数 人,
答:参加此次竞赛活动成绩优秀 的学生人数是468人.
21. 【答案】
(1) 初中 名选手的平均分 ,众数 ,
高中 名选手的成绩是:,,,,,故中位数 ;
(2) 由表格可知初中部与高中部的平均分相同,初中部的中位数高,故初中部决赛成绩较好;
(3)
,
初中代表队选手成绩比较稳定.
22. 【答案】
(1) ;
(2) ①
②当 时,,(万).
当 时,,(万).
当 时,,(万).
当 时,,(万).
(万),
最早到 周,该地区可达到实现全民免疫的标准.
(3) 当 时,.
当 时,有 ,解得 .
.
当 时,.
当 时,.
根据题意,得 ,解得 .
该地区的建议接种人群最早将于第 周全部完成接种.
【解析】
(1) 这八周中每周接种人数的平均数为 (万).
由扇形统计图得 所占百分比为 ,
则该地区的总人口约为 (万).
(2) ①当 时,.
第 周的接种人数约为 万.
一、选择题(共12题)
已知小华上学期语文、数学、英语三科平均分为 分,他记得语文得了 分,英语得了 分,但他把数学成绩忘记了,你能告诉他应该是以下哪个分数吗?
A. B. C. D.
某单位要招聘 名英语翻译,张明参加招聘考试的成绩如表所示:若把听、说、读、写的成绩按 计算平均成绩,则张明的平均成绩为
A. B. C. D.
某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
该店主决定本周进货时,增加了一些 码的衬衫,影响该店主决策的统计量是
A.众数 B.方差 C.平均数 D.中位数
某射击小组有 人,教练根据他们某次射击命中环数的数据绘制成如图的统计图,则这组数据的众数和极差分别是
A. , B. , C. , D. ,
某校在体育健康测试中,有 名男生“引体向上”的成绩(单位:次)分别是:,,,,,,,,这组数据的中位数和众数分别是
A. , B. , C. , D. ,
第七届世界军人运动会将于 年 月 日至 日在武汉举行.光谷某中学开展了“助力军动会”志愿者招募活动,同学们踊跃报名参与竞选.经选拔,最终每个班级都有同学光荣晋升为本次军运会志愿者.下面的条形统计图描述了这些班级选拔出的志愿者人数的情况;下列说法错误的是
A.参加竞选的共有 个班级 B.本次竞选共选拔出 名志愿者
C.各班选拔出的志愿者人数的众数为 D.各班选拔出的志愿者人数的中位数为
如图为甲,乙,丙,丁四名射击运动员在赛前的某次射击选拔赛中,各射击 次成绩的折线图和表示平均数的水平线,经过计算,四人成绩的方差关系为:,,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择
A.甲 B.乙 C.丙 D.丁
若样本 ,,,, 的平均数为 ,方差为 ,则对于样本 ,,,,,下列结论正确的是
A.平均数为 ,方差为 B.平均数为 ,方差为
C.平均数为 ,方差为 D.平均数为 ,方差为
为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的 , 和 .为合理确定各档之间的界限,随机抽查了该市 万户居民家庭上一年的年用水量(单位:),绘制了统计图,如图所示,下面有四个推断:
①年用水量不超过 的该市居民家庭按第一档水价交费;
②年用水量超过 的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在 之间;
④该市居民家庭年用水量的平均数不超过 ;
其中合理的是
A.①③ B.①④ C.②③ D.②④
为了解某校 名初三学生的睡眠时间,从中抽取 名学生进行调查,在这个问题中,下列说法正确的是
A. 名学生是总体 B. 是众数
C. 名学生是抽取的一个样本 D. 是样本的容量
某校共有 名学生,为了解本学期学生参加公益劳动的情况,收集了他们参加公益劳动时间(单位:)等数据,以下是根据数据绘制的统计图表的一部分:
下面有四个推断:
①这 名学生参加公益劳动时间的平均数一定在 之间;
②这 名学生参加公益劳动时间的中位数在 之间;
③这 名学生中,初中生参加公益劳动时间的中位数一定在 之间;
④这 名学生中,高中生参加公益劳动时间的中位数可能在 之间.
所有合理推断的序号是
A.①③ B.②④ C.①②③ D.①②③④
某电脑公司销售部为定制下个月的销售计划,对 名销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这 名销售员本月销售量的平均数、中位数、众数分别是
A. ,, B. ,, C. ,, D. ,,
二、填空题(共5题)
回顾所学,完善本课的知识结构图.
将一组数据中的每一个数都加上 得到一组新的数据,那么在众数、中位数、平均数、方差这四个统计量中,值保持不变的是 .
某校五个绿化小组植树的棵数如下:,,,,,已知这组数据的众数与平均数相等,那么这组数据的中位数是 .
若一组数据 ,,,, 的众数为 ,则这组数据的方差为 .
第 届冬季奥林匹克运动会于 年 月在北京市和张家口市联合举行,某校寒假期间组织部分滑雪爱好者参加冬令营集训,训练期间,冬令营的同学们都参加了“单板滑雪”这个项目 次的训练测试,每次测试成绩分别为 分, 分, 分, 分, 分五档,甲,乙两位同学在这个项目的测试成绩统计结果如图所示.
根据上图判断,甲同学测试成绩的众数是 ;乙同学测试成绩的中位数是 ;甲,乙两位同学中单板滑雪成绩更稳定的是 .
三、解答题(共5题)
某市教育行政部门为了解初三学生每学期参加综合实践活动的情况,随机抽样调查了某校初三学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图 ,图 ).请你根据图中提供的信息,回答下列问题:
(1) 该校初三学生总数为 人;
(2) 分别求出活动时间为 天、 天的学生人数为 , ,并补全频数分布直方图;
(3) 扇形统计图中“活动时间为 天”的扇形所对圆心角的度数是 ;
(4) 在这次抽样调查中,众数和中位数分别是 , ;
(5) 如果该市共有初三学生 人,请你估计“活动时间不少于 天”的大约有多少人?
某校为了解该校九年级学生一模测试数学成绩,现从九年级学生中随机抽取部分学生的一模测试数学成绩,按A,B,C,D,E五个等级进行统计,并将统计结果绘制成如图所示不完整的统计图,请根据统计图中的信息解答下列问题:
(1) 此次抽查的学生人数为 ,补全条形统计图.
(2) 在抽取的学生中,一模测试数学成绩的中位数落在 等级;
(3) 试求样本扇形图中,“E等级”所对扇形圆心角的度数.
动手做一做.
每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某校为确保学生安全,开展了“远离溺水·珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用 表示,共分成四组:A.,B.,C.,D.),下面给出了部分信息:
七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
八年级10名学生的竞赛成绩在C组中的数据是:94,90,94
七、八年级抽取的学生竞赛成绩统计表
根据以上信息,解答下列问题:
(1) (1)直接写出上述图表中 ,, 的值;
(2) (2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3) (3)该校七、八年级共720人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀 的学生人数是多少?
我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出 名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的 名选手的决赛成绩如图所示.
(1) 根据图示计算出 ,, 的值;
(2) 结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3) 计算初中代表队决赛成绩的方差 ,并判断哪一个代表队选手成绩较为稳定.
为了防控新冠疫情,某地区积极推广疫苗接种工作,卫生防疫部门对该地区八周以来的相关数据进行收集整理,绘制得到如下图表:
该地区每周接种疫苗人数统计表
根据统计表中的数据,建立以周次为横坐标,接种人数为纵坐标的平面直角坐标系,并根据以上统计表中的数据描出对应的点,发现从第 周开始这些点大致分布在一条直线附近,现过其中两点 , 作一条直线(如图所示,该直线的函数表达式为 ),那么这条直线可近似反映该地区接种人数的变化趋势.
请根据以上信息,解答下列问题:
(1) 这八周中每周接种人数的平均数为 万;该地区的总人口约为 万;
(2) 若从第 周开始,每周的接种人数仍符合上述变化趋势.
①估计第 周的接种人数为 万;
②专家表示:疫苗接种率至少达 ,才能实现全民免疫.那么,从推广疫苗接种工作开始,最早到第几周,该地区可达到实现全民免疫的标准?
(3) 实际上,受疫苗供应等客观因素影响,从第 周开始,接种人数将会逐周减少 万,为了尽快提高接种率,一旦周接种人数低于 万时,卫生防疫部门将会采取措施,使得之后每周的接种人数一直维持在 万.如果 ,那么该地区的建议接种人群最早将于第几周全部完成接种?
答案
一、选择题(共12题)
1. 【答案】A
2. 【答案】C
3. 【答案】A
【解析】 码衬衫出现次数最多,
影响店主决策的统计量是众数.
4. 【答案】D
【解析】由条形统计图可知 出现的次数最多,则众数是 (环);
这组数据的最大值是 ,最小值是 ,则极差是 .
5. 【答案】C
【解析】原数据按由小到大排列为:,,,,,,,,
所以这组数据的中位数 ,众数为 .
故答案选C.
6. 【答案】C
7. 【答案】A
8. 【答案】A
【解析】样本 ,,,,,对于样本 ,,,, 来说,
每个数据均在原来的基础上增加了 ,根据平均数、方差的变化规律得:
平均数较前增加 ,而方差不变,即:平均数为 ,方差为 .
9. 【答案】B
【解析】提示:年用水量不超过 的占 .①中推理合理;
年用水量超过 的占 .②中推理不合理;
中位数在 之间;
年用水量的平均数约为 .
10. 【答案】D
11. 【答案】C
【解析】思路分析:通过频数分布表及统计图得到数据信息,再根据中位数与平均数的定义求解即可.
①这 名学生参加公益劳动时间的平均数为 ,一定在 之间,故①正确;
②由统计表类别栏计算可得,各时间段人数分别为 ,,,,,则中位数在 之间,故②正确.
③由统计表计算可得,初中学段栏中 的时间段的人数在 之间,当人数为 时,中位数在 之间;当人数为 时,中位数在 之间,故③正确.
④由统计表计算可得,高中学段各时间段人数分别为 ,,,,,当 时间段的人数为 时,中位数在 之间,当 时间段的人数为 时,中位数在 之间,故④错误.
故选:C.
12. 【答案】C
二、填空题(共5题)
13. 【答案】频数分布直方图;平均水平;波动程度;分布;频数
14. 【答案】方差
【解析】将一组数据中的每一个数都加上 得到一组新的数据,那么这组数据的波动幅度保持不变,即方差不变,而平均数和众数、中位数均改变.
故答案为:方差.
15. 【答案】
【解析】可知 ,,,, 的众数与平均数都是 ,
故 ,解得:,
将数据排列后得:,,,,,故中位数为 .
16. 【答案】
【解析】 数据 ,,,, 的众数为 ,
,
,
.
17. 【答案】 ; ;乙
三、解答题(共5题)
18. 【答案】
(1)
(2) ;
补全频数分布直方图如图所示:
(3)
(4) ;
(5) (人).
答:该市初三学生 人中“活动时间不少于 天”的大约有 人.
【解析】
(1) ,
故答案为:.
(2) 人,
人,
故答案为:,.
(3) .
故答案为:.
(4) 综合实践活动时间为 天的出现次数最多,是 次,因此众数是 天,
将综合实践时间从小到大排列后处在第 , 位的都是 天,因此中位数是 天,
故答案为:,.
19. 【答案】
(1) 人
补图略.
(2) C
(3) .
20. 【答案】
(1) (1),
∵八年级10名学生的竞赛成绩的中位数是第5和第6个数据的平均数,
∴ ;
∵在七年级10名学生的竞赛成绩中99出现的次数最多,
∴ ;
(2) (2)八年级学生掌握防溺水安全知识较好,理由:虽然七、八年级的平均分均为92分,但八年级的中位数和众数均高于七年级.
(3) (3)参加此次竞赛活动成绩优秀 的学生人数 人,
答:参加此次竞赛活动成绩优秀 的学生人数是468人.
21. 【答案】
(1) 初中 名选手的平均分 ,众数 ,
高中 名选手的成绩是:,,,,,故中位数 ;
(2) 由表格可知初中部与高中部的平均分相同,初中部的中位数高,故初中部决赛成绩较好;
(3)
,
初中代表队选手成绩比较稳定.
22. 【答案】
(1) ;
(2) ①
②当 时,,(万).
当 时,,(万).
当 时,,(万).
当 时,,(万).
(万),
最早到 周,该地区可达到实现全民免疫的标准.
(3) 当 时,.
当 时,有 ,解得 .
.
当 时,.
当 时,.
根据题意,得 ,解得 .
该地区的建议接种人群最早将于第 周全部完成接种.
【解析】
(1) 这八周中每周接种人数的平均数为 (万).
由扇形统计图得 所占百分比为 ,
则该地区的总人口约为 (万).
(2) ①当 时,.
第 周的接种人数约为 万.
