2023春人教版五年级数学下册1.因数和倍数(课件)(共36张PPT)
文档属性
| 名称 | 2023春人教版五年级数学下册1.因数和倍数(课件)(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-06 16:17:31 | ||
图片预览











文档简介
(共36张PPT)
2023春 人教数学
五年级下册
人教版数学五年级(下)
因数和倍数
1. 因数和倍数的认识
2
课堂导入
唐僧
孙悟空
大家喜欢看《西游记》吗
他们是谁
他们是什么关系
他们是师徒关系。
唐僧是孙悟空的师傅,
孙悟空是唐僧的徒弟。
老师和同学们之间是什么关系
师生关系。
不仅人与人之间存在着关系,在数学中,
数与数之间也存在着关系。
今天我们就来研究两个自然数之间的关系。
新知探究
教材第5页例1
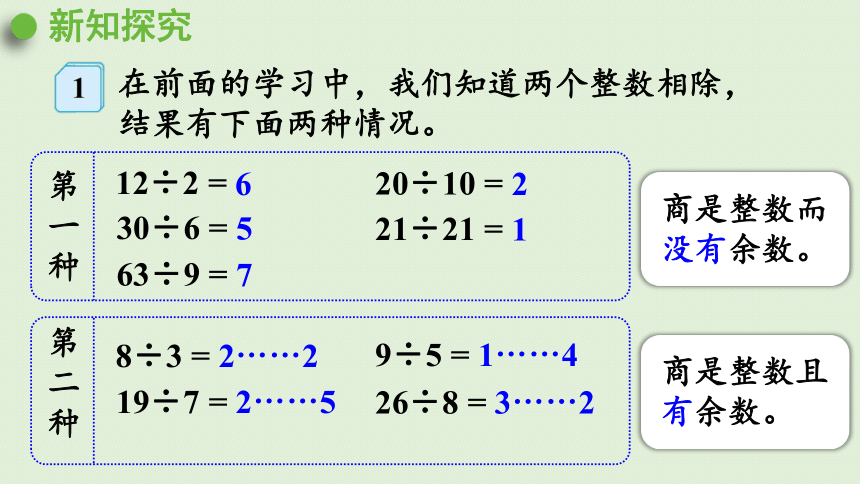
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
8÷3 = 2……2
30÷6 =
19÷7 = 2……5
21÷21 =
63÷9 =
9÷5 = 1……4
26÷8 = 3……2
6
5
2
1
7
第
一
种
第
二
种
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
8÷3 = 2……2
30÷6 =
19÷7 = 2……5
21÷21 =
63÷9 =
9÷5 = 1……4
26÷8 = 3……2
6
5
2
1
7
第
一
种
第
二
种
商是整数且没有余数。
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
8÷3 = 2……2
30÷6 =
19÷7 = 2……5
21÷21 =
63÷9 =
9÷5 = 1……4
26÷8 = 3……2
6
5
2
1
7
第
一
种
第
二
种
商是整数而没有余数。
商是整数且有余数。
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
8÷3 = 2……2
30÷6 =
19÷7 = 2……5
21÷21 =
63÷9 =
9÷5 = 1……4
26÷8 = 3……2
6
5
2
1
7
第
一
种
第
二
种
商是整数而没有余数。
商是整数而有余数。
在整数除法中,如果商是整数且没有余数(或者说余数为0),我们就说除数是被除数的因数(也称约数),被除数是除数的倍数。
新知探究
教材第5页例1
在整数除法中,如果商是整数且没有余数(或者说余数为0),我们就说除数是被除数的因数(也称约数),被除数是除数的倍数。
例如:12÷2 = 6
,2是12的因数
,12是2的倍数;
12÷6 = 2
,6是12的因数
,12是6的倍数;
2×6 = 12
,2和6是12的因数,
12是2和6的倍数。
新知探究
教材第5页例1
例如:12÷2 = 6
,2是12的因数
,12是2的倍数;
12÷6 = 2
,6是12的因数
,12是6的倍数;
2×6 = 12
,2和6是12的因数,
12是2和6的倍数。
在整数除法中,如果商是整数且没有余数,那么除数和商是被除数的因数,被除数是除数和商的倍数。
在整数乘法中,两个乘数都是积的因数,积是两个乘数的倍数。
在除法算式a÷b=c(a、b、c均为非0自然数)中,a是b、c的倍数,b、c是a的因数。
在乘法算式b×c=a(a、b、c均为非0自然数)中,b、c是a的因数,a是b、c的倍数。
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
30÷6 =
21÷21 =
63÷9 =
6
5
2
1
7
第
一
种
说一说上面的其他算式中,谁是谁的因数 谁是谁的倍数
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
30÷6 =
21÷21 =
63÷9 =
6
5
2
1
7
第
一
种
30÷6 = 5 , 和 是 的因数;
是 和 的倍数。
6
5
30
30
6
5
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
30÷6 =
21÷21 =
63÷9 =
6
5
2
1
7
第
一
种
63÷9 = 7 , 和 是 的因数;
是 和 的倍数。
9
7
63
63
9
7
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
30÷6 =
21÷21 =
63÷9 =
6
5
2
1
7
第
一
种
20÷10 = 2 , 和 是 的因数;
是 和 的倍数。
10
2
20
20
10
2
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
30÷6 =
21÷21 =
63÷9 =
6
5
2
1
7
第
一
种
21÷21 = 1 , 和 是 的因数;
是 和 的倍数。
21
1
21
21
21
1
新知探究
教材第5页例1
21÷21 = 1 , 和 是 的因数;
是 和 的倍数。
21
1
21
21
21
1
20÷10 = 2 , 和 是 的因数;
是 和 的倍数。
10
2
20
20
10
2
63÷9 = 7 , 和 是 的因数;
是 和 的倍数。
9
7
63
63
9
7
30÷6 = 5 , 和 是 的因数;
是 和 的倍数。
6
5
30
30
6
5
12÷2 = 6 , 和 是 的因数;
是 和 的倍数。
2
6
12
12
2
6
必须要说谁是谁的因数,谁是谁的倍数。因数和倍数是相互依存的。
注意:为了方便,在研究因数和倍数的时候,我们所指的数是自然数(一般不包括0)。
下面的四组数中,谁是谁的因数 谁是谁的倍数
教材第5页“做一做”
4和24
26和13
75和25
81和9
4是24的因数
,24是4的倍数。
13是26的因数
,26是13的倍数。
25是75的因数
,75是25的倍数。
9是81的因数
,81是9的倍数。
倍数和因数
1. 在除法算式a÷b=c(a、b、c均为非0自然数)中,a是b、c的倍数,b、c是a的因数。
在乘法算式b×c=a(a、b、c均为非0自然数)中,b、c是a的因数,a是b、c的倍数。
2. 为了方便,在研究因数和倍数的时候,我们
所指的数是自然数(一般不包括0)。
18的因数有
18的因数有哪些
1 , 18
18÷1 = 18
18÷2 = 9
18÷3 = 6
18÷4 = 4……2
18÷5 = 3……3
18÷6 = 3
×
×
, 2 , 9
, 3 , 6。
1×18 = 18
2×9 = 18
1 , 2 , 3 , 6 , 9 , 18。
3×6 = 18
18的因数有
18的因数
1,2,3,
6,9,18
18有6个因数。
1 , 2 , 3 , 6 , 9 , 18。
18的因数有哪些
30的因数有哪些 36呢
30÷1 = 30
30÷2 = 15
30÷3 = 10
30÷5 = 6
30的因数
1,2,3,
5,6,10,
15,30
36的因数
1,2,3,
4,6,9,
12,18,36
1×36 = 36
2×18 = 36
3×12 = 36
4×9 = 36
6×6 = 36
30有8个因数。
36有9个因数。
一个数的因数的个数是有限的。
从上面找因数的过程中,你有什么发现
一个数的最小因数是1,
最大因数
是它本身。
一个数的因数的个数是有限的。
找一个数的因数
1.可以用列除法算式或列乘法算式的方法找一个数的因数。表示时,可以用列举法或用集合图的方法表示。
2.一个数的因数的个数是有限的,它的最小因
数是1,最大因数是它本身。
2的倍数有哪些
2×1 = 2
2×2 = 4
2×3 = 6
……
2的倍数有2,4,6,…。
怎样找2的倍数呢
2的倍数
2,4,6,
8,10,12,
14,…
2的倍数有无数个。
2÷2 = 1
4÷2 = 2
6÷2 = 3
……
3的倍数有哪些 5呢
3÷3 = 1
6÷3 = 2
9÷3 = 3
……
3的倍数
3,6,9,
12,15,18,
…
5的倍数
5,10,15,
20,25,30,
35,…
5×1 = 5
5×2 = 10
5×3 = 15
……
一个数的倍数的个数是无限的。
从上面找倍数的过程中,你有什么发现
一个数的最小倍数是它本身,
没有
最大倍数。
一个数的倍数的个数是无限的。
找一个数的倍数
1.可以用列除法算式或列乘法算式的方法找一个数的倍数。表示时,可以用列举法或用集合图的方法表示。
2. 一个数的倍数的个数是无限的,它的最小倍数是它本身,没有最大倍数。
从上面找因数和倍数的过程中,你有什么发现
一个数的最小因数是1,
一个数的最小倍数是它本身,
最大因数
是它本身。
没有
最大倍数。
一个数的因数的个数是有限的,一个数的倍数的个数是无限的。
写一写
(1)写出下面各数的因数。
1 17 22 24
课堂练习
1
1,17。
1,2,
11,22。
1,2,3,
4,6,8,
12,24。
一对一对地找,即想哪两个数相乘的积等于这个数,那么这两个数都是这个数的因数。
写一写
(2)写出下面各数的倍数(各写5个)。
1 7 9 10
课堂练习
1,2,3,4,5
7,14,21,28,35
9,18,27,36,45
10,20,30,40,50
用这个数分别去乘1,2,3,…所得的积都是这个数的倍数。
(1) 9×6 = 54,下面说法中正确的是( )。
6和9是因数
54是倍数
6和9是54的因数
C
C.
选一选
在说一个数的因数或倍数时,应说“谁是谁的因数”或“谁是谁的倍数”,而不能单独说某一个数或几个数是因数或倍数。
因为37÷37=1,所以37是37的( )。
C
选一选
(2)
A. 因数 B. 倍数 C. 因数或倍数
C.
(3)15是( )的倍数,15是( )的因数。
A. 1和15 B.15和30 C. 1、15、30
A.
A
B
B.
(1) 12的因数一共有4个。 ( )
(2) 10、12、33、45……都是1的倍数。 ( )
×
辨一辨
(3) 2的倍数比20的倍数多。 ( )
√
一个数的倍数是无限的。
一个数的最小因数是1。
12的因数有1,2,3,4,6,12。
×
1. 一个数是8的因数,又是12的因数,这个数是( )。
2. 一个数是8的倍数,又是24的因数,这个数是( )。
拓展提升
可以根据条件先分别找出一个数的因数或倍数,再通过观察比较,得出结论。
猜一猜
1,2,3,4,6,12。
1
2
4
1,2,4,8。
8,16,24,……
1,2,3,4,6,8,12,24。
8
24
A:除4之外的4的倍数 B:它的最大因数是6
C:只有因数1和2 D:只有一个因数
E:最大的一位数 F:5的最小倍数
G:它的因数有1,2,4 H:是E和F的差
这个电话号码是( )。
86219544
3. 猜电话号码。
8
6
2
1
9
5
4
9-5=4
课堂小结
同学们,这节课你有哪些收获?
2023春 人教数学
五年级下册
人教版数学五年级(下)
因数和倍数
1. 因数和倍数的认识
2
课堂导入
唐僧
孙悟空
大家喜欢看《西游记》吗
他们是谁
他们是什么关系
他们是师徒关系。
唐僧是孙悟空的师傅,
孙悟空是唐僧的徒弟。
老师和同学们之间是什么关系
师生关系。
不仅人与人之间存在着关系,在数学中,
数与数之间也存在着关系。
今天我们就来研究两个自然数之间的关系。
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
8÷3 = 2……2
30÷6 =
19÷7 = 2……5
21÷21 =
63÷9 =
9÷5 = 1……4
26÷8 = 3……2
6
5
2
1
7
第
一
种
第
二
种
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
8÷3 = 2……2
30÷6 =
19÷7 = 2……5
21÷21 =
63÷9 =
9÷5 = 1……4
26÷8 = 3……2
6
5
2
1
7
第
一
种
第
二
种
商是整数且没有余数。
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
8÷3 = 2……2
30÷6 =
19÷7 = 2……5
21÷21 =
63÷9 =
9÷5 = 1……4
26÷8 = 3……2
6
5
2
1
7
第
一
种
第
二
种
商是整数而没有余数。
商是整数且有余数。
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
8÷3 = 2……2
30÷6 =
19÷7 = 2……5
21÷21 =
63÷9 =
9÷5 = 1……4
26÷8 = 3……2
6
5
2
1
7
第
一
种
第
二
种
商是整数而没有余数。
商是整数而有余数。
在整数除法中,如果商是整数且没有余数(或者说余数为0),我们就说除数是被除数的因数(也称约数),被除数是除数的倍数。
新知探究
教材第5页例1
在整数除法中,如果商是整数且没有余数(或者说余数为0),我们就说除数是被除数的因数(也称约数),被除数是除数的倍数。
例如:12÷2 = 6
,2是12的因数
,12是2的倍数;
12÷6 = 2
,6是12的因数
,12是6的倍数;
2×6 = 12
,2和6是12的因数,
12是2和6的倍数。
新知探究
教材第5页例1
例如:12÷2 = 6
,2是12的因数
,12是2的倍数;
12÷6 = 2
,6是12的因数
,12是6的倍数;
2×6 = 12
,2和6是12的因数,
12是2和6的倍数。
在整数除法中,如果商是整数且没有余数,那么除数和商是被除数的因数,被除数是除数和商的倍数。
在整数乘法中,两个乘数都是积的因数,积是两个乘数的倍数。
在除法算式a÷b=c(a、b、c均为非0自然数)中,a是b、c的倍数,b、c是a的因数。
在乘法算式b×c=a(a、b、c均为非0自然数)中,b、c是a的因数,a是b、c的倍数。
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
30÷6 =
21÷21 =
63÷9 =
6
5
2
1
7
第
一
种
说一说上面的其他算式中,谁是谁的因数 谁是谁的倍数
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
30÷6 =
21÷21 =
63÷9 =
6
5
2
1
7
第
一
种
30÷6 = 5 , 和 是 的因数;
是 和 的倍数。
6
5
30
30
6
5
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
30÷6 =
21÷21 =
63÷9 =
6
5
2
1
7
第
一
种
63÷9 = 7 , 和 是 的因数;
是 和 的倍数。
9
7
63
63
9
7
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
30÷6 =
21÷21 =
63÷9 =
6
5
2
1
7
第
一
种
20÷10 = 2 , 和 是 的因数;
是 和 的倍数。
10
2
20
20
10
2
新知探究
教材第5页例1
在前面的学习中,我们知道两个整数相除,结果有下面两种情况。
12÷2 =
20÷10 =
30÷6 =
21÷21 =
63÷9 =
6
5
2
1
7
第
一
种
21÷21 = 1 , 和 是 的因数;
是 和 的倍数。
21
1
21
21
21
1
新知探究
教材第5页例1
21÷21 = 1 , 和 是 的因数;
是 和 的倍数。
21
1
21
21
21
1
20÷10 = 2 , 和 是 的因数;
是 和 的倍数。
10
2
20
20
10
2
63÷9 = 7 , 和 是 的因数;
是 和 的倍数。
9
7
63
63
9
7
30÷6 = 5 , 和 是 的因数;
是 和 的倍数。
6
5
30
30
6
5
12÷2 = 6 , 和 是 的因数;
是 和 的倍数。
2
6
12
12
2
6
必须要说谁是谁的因数,谁是谁的倍数。因数和倍数是相互依存的。
注意:为了方便,在研究因数和倍数的时候,我们所指的数是自然数(一般不包括0)。
下面的四组数中,谁是谁的因数 谁是谁的倍数
教材第5页“做一做”
4和24
26和13
75和25
81和9
4是24的因数
,24是4的倍数。
13是26的因数
,26是13的倍数。
25是75的因数
,75是25的倍数。
9是81的因数
,81是9的倍数。
倍数和因数
1. 在除法算式a÷b=c(a、b、c均为非0自然数)中,a是b、c的倍数,b、c是a的因数。
在乘法算式b×c=a(a、b、c均为非0自然数)中,b、c是a的因数,a是b、c的倍数。
2. 为了方便,在研究因数和倍数的时候,我们
所指的数是自然数(一般不包括0)。
18的因数有
18的因数有哪些
1 , 18
18÷1 = 18
18÷2 = 9
18÷3 = 6
18÷4 = 4……2
18÷5 = 3……3
18÷6 = 3
×
×
, 2 , 9
, 3 , 6。
1×18 = 18
2×9 = 18
1 , 2 , 3 , 6 , 9 , 18。
3×6 = 18
18的因数有
18的因数
1,2,3,
6,9,18
18有6个因数。
1 , 2 , 3 , 6 , 9 , 18。
18的因数有哪些
30的因数有哪些 36呢
30÷1 = 30
30÷2 = 15
30÷3 = 10
30÷5 = 6
30的因数
1,2,3,
5,6,10,
15,30
36的因数
1,2,3,
4,6,9,
12,18,36
1×36 = 36
2×18 = 36
3×12 = 36
4×9 = 36
6×6 = 36
30有8个因数。
36有9个因数。
一个数的因数的个数是有限的。
从上面找因数的过程中,你有什么发现
一个数的最小因数是1,
最大因数
是它本身。
一个数的因数的个数是有限的。
找一个数的因数
1.可以用列除法算式或列乘法算式的方法找一个数的因数。表示时,可以用列举法或用集合图的方法表示。
2.一个数的因数的个数是有限的,它的最小因
数是1,最大因数是它本身。
2的倍数有哪些
2×1 = 2
2×2 = 4
2×3 = 6
……
2的倍数有2,4,6,…。
怎样找2的倍数呢
2的倍数
2,4,6,
8,10,12,
14,…
2的倍数有无数个。
2÷2 = 1
4÷2 = 2
6÷2 = 3
……
3的倍数有哪些 5呢
3÷3 = 1
6÷3 = 2
9÷3 = 3
……
3的倍数
3,6,9,
12,15,18,
…
5的倍数
5,10,15,
20,25,30,
35,…
5×1 = 5
5×2 = 10
5×3 = 15
……
一个数的倍数的个数是无限的。
从上面找倍数的过程中,你有什么发现
一个数的最小倍数是它本身,
没有
最大倍数。
一个数的倍数的个数是无限的。
找一个数的倍数
1.可以用列除法算式或列乘法算式的方法找一个数的倍数。表示时,可以用列举法或用集合图的方法表示。
2. 一个数的倍数的个数是无限的,它的最小倍数是它本身,没有最大倍数。
从上面找因数和倍数的过程中,你有什么发现
一个数的最小因数是1,
一个数的最小倍数是它本身,
最大因数
是它本身。
没有
最大倍数。
一个数的因数的个数是有限的,一个数的倍数的个数是无限的。
写一写
(1)写出下面各数的因数。
1 17 22 24
课堂练习
1
1,17。
1,2,
11,22。
1,2,3,
4,6,8,
12,24。
一对一对地找,即想哪两个数相乘的积等于这个数,那么这两个数都是这个数的因数。
写一写
(2)写出下面各数的倍数(各写5个)。
1 7 9 10
课堂练习
1,2,3,4,5
7,14,21,28,35
9,18,27,36,45
10,20,30,40,50
用这个数分别去乘1,2,3,…所得的积都是这个数的倍数。
(1) 9×6 = 54,下面说法中正确的是( )。
6和9是因数
54是倍数
6和9是54的因数
C
C.
选一选
在说一个数的因数或倍数时,应说“谁是谁的因数”或“谁是谁的倍数”,而不能单独说某一个数或几个数是因数或倍数。
因为37÷37=1,所以37是37的( )。
C
选一选
(2)
A. 因数 B. 倍数 C. 因数或倍数
C.
(3)15是( )的倍数,15是( )的因数。
A. 1和15 B.15和30 C. 1、15、30
A.
A
B
B.
(1) 12的因数一共有4个。 ( )
(2) 10、12、33、45……都是1的倍数。 ( )
×
辨一辨
(3) 2的倍数比20的倍数多。 ( )
√
一个数的倍数是无限的。
一个数的最小因数是1。
12的因数有1,2,3,4,6,12。
×
1. 一个数是8的因数,又是12的因数,这个数是( )。
2. 一个数是8的倍数,又是24的因数,这个数是( )。
拓展提升
可以根据条件先分别找出一个数的因数或倍数,再通过观察比较,得出结论。
猜一猜
1,2,3,4,6,12。
1
2
4
1,2,4,8。
8,16,24,……
1,2,3,4,6,8,12,24。
8
24
A:除4之外的4的倍数 B:它的最大因数是6
C:只有因数1和2 D:只有一个因数
E:最大的一位数 F:5的最小倍数
G:它的因数有1,2,4 H:是E和F的差
这个电话号码是( )。
86219544
3. 猜电话号码。
8
6
2
1
9
5
4
9-5=4
课堂小结
同学们,这节课你有哪些收获?
