因数与倍数(课件)西师大版五年级下册数学(共25张PPT)
文档属性
| 名称 | 因数与倍数(课件)西师大版五年级下册数学(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 16.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-06 07:01:40 | ||
图片预览


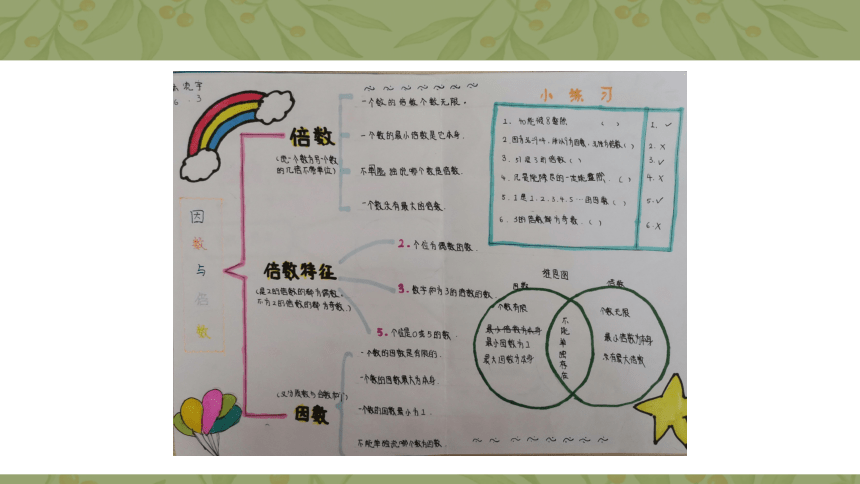
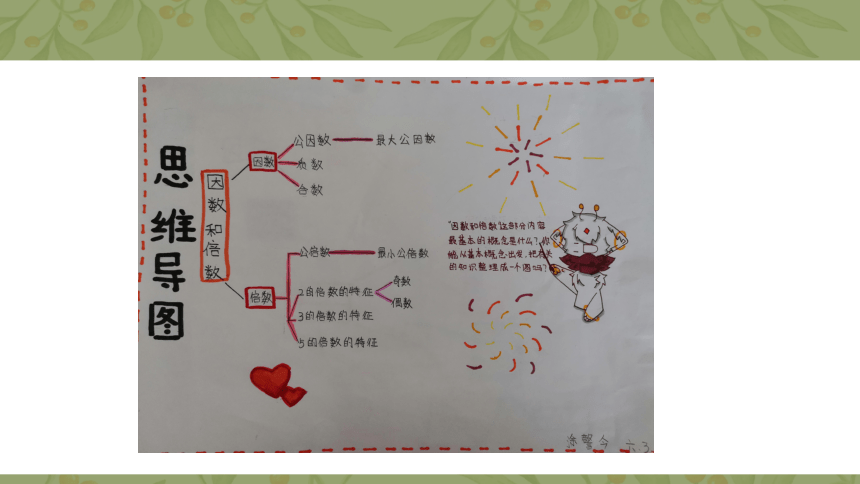


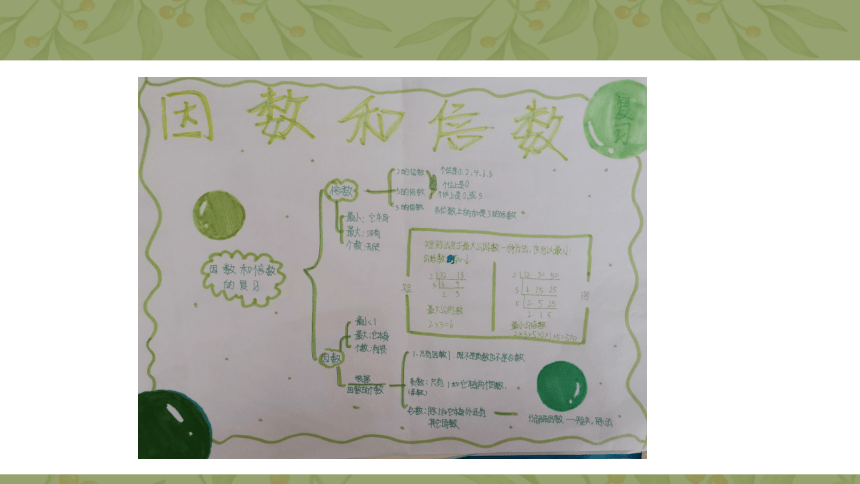


文档简介
(共25张PPT)
因数与倍数
表示物体个数的0,1,2,3,4,5……这些数都是自然数。
你能用一个算式介绍一下因数和倍数吗?
因数和倍数是两个相互依存的概念,不能单独存在。
45÷15=3
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
用不同颜色的笔,分别圈出12的因数和12的倍数
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
2的倍数的特征是:个位上的数是2,4,6,8或0。
倍数
自
然
数
奇数
偶数
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
3的倍数的特征是:各个数位上的数字的和是3的倍数
倍数
公倍数:几个数公有的倍数,叫做这几个数的公倍数。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
倍数
45
15
25
90
35
55
65
75
85
95
10
20
30
40
50
60
70
80
100
5
5的倍数的特征是:个位上的数是5或0。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
45
15
25
90
35
55
65
75
85
95
10
20
30
40
50
60
70
80
100
5
:只有1和它本身两个因数的数。
除了1和它本身还有别的因数。
1既不是质数也不是合数,因为它只有一个因数。
非零自然数
质数(或素数)
合数:
“1”:
因数
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
倍数
45
15
25
90
35
55
65
75
85
95
10
20
30
40
50
60
70
80
100
选择一个合数写成质数相乘的形式(分解质因数)
4 2
2
2 1
3
7
42=2×3×7
用质数做除数,除到商是质数为止。
求下面数的最小公倍数和最大公因数
8和36
6和18
11和13
4 18
2
8 36
2
2 9
最大公因数是2×2=4。
最小公倍数是2×2×2×9=72。
最大公因数是6。
最小公倍数是18。
最小公倍数是143。
最大公因数是1。
1.如果两个数是倍数关系,那么他们的最小公倍数是大的那个数,最大公因数是小的那个数。
2.如果两个数互质,那么他们的最小公倍数是他们的乘积,最大公因数是1。
判断:
2.合数一定都是偶数。
1.质数一定都是奇数。
×
×
×
4.一个非零自然数不是质数就是合数。
3.一个自然数不是奇数就是偶数。
√
×
6.一个数的因数一定比它的倍数小。
5.因为10÷4=2.5,4是10的因数,10是4的倍数。
×
练习
1. 既是质数又是偶数 ( )
2. 最小的合数( )
3. 7的最大因数( )
4. 最小的质数( )
5. 两个最小质数的和( )
6. 10以内既是奇数又是合数( )
7. 一位数中最大的偶数( )
8. 既不是质数又不是合数( )
这个号码是( )
老师的QQ号码排列如下:
1
2
4
7
2
5
9
8
24725981
练习
(1)如果A=2×3×5,B=2×3×3,A和B的最大公因数是( ),最小公倍数是( )。
填空:
(2)如果A÷B=5(A,B为自然数,B≠0),那么A,B的最大公因数是( ),最小公倍数是( )。
6
90
B
A
练习
5×8=40(分)
答:至少再过40分又同时发车。
23路公交车每5分发车一次,6路公交车每8分发车一次,这两路车同时发车后,至少再过多少时间又同时发车?
练习
有两根木棒,分别长12厘米、44厘米,要把他们截成同样长的小木棒,且没有剩余,每根小木棒最长是多少厘米?
2
2
3 11
12 44
6 22
答:每根小木棒最长4厘米。
2×2=4(厘米)
这节课的复习之后,与复习之前相比你有哪些提升?
因数与倍数
表示物体个数的0,1,2,3,4,5……这些数都是自然数。
你能用一个算式介绍一下因数和倍数吗?
因数和倍数是两个相互依存的概念,不能单独存在。
45÷15=3
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
用不同颜色的笔,分别圈出12的因数和12的倍数
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
2的倍数的特征是:个位上的数是2,4,6,8或0。
倍数
自
然
数
奇数
偶数
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
3的倍数的特征是:各个数位上的数字的和是3的倍数
倍数
公倍数:几个数公有的倍数,叫做这几个数的公倍数。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
倍数
45
15
25
90
35
55
65
75
85
95
10
20
30
40
50
60
70
80
100
5
5的倍数的特征是:个位上的数是5或0。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
45
15
25
90
35
55
65
75
85
95
10
20
30
40
50
60
70
80
100
5
:只有1和它本身两个因数的数。
除了1和它本身还有别的因数。
1既不是质数也不是合数,因为它只有一个因数。
非零自然数
质数(或素数)
合数:
“1”:
因数
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
倍数
45
15
25
90
35
55
65
75
85
95
10
20
30
40
50
60
70
80
100
选择一个合数写成质数相乘的形式(分解质因数)
4 2
2
2 1
3
7
42=2×3×7
用质数做除数,除到商是质数为止。
求下面数的最小公倍数和最大公因数
8和36
6和18
11和13
4 18
2
8 36
2
2 9
最大公因数是2×2=4。
最小公倍数是2×2×2×9=72。
最大公因数是6。
最小公倍数是18。
最小公倍数是143。
最大公因数是1。
1.如果两个数是倍数关系,那么他们的最小公倍数是大的那个数,最大公因数是小的那个数。
2.如果两个数互质,那么他们的最小公倍数是他们的乘积,最大公因数是1。
判断:
2.合数一定都是偶数。
1.质数一定都是奇数。
×
×
×
4.一个非零自然数不是质数就是合数。
3.一个自然数不是奇数就是偶数。
√
×
6.一个数的因数一定比它的倍数小。
5.因为10÷4=2.5,4是10的因数,10是4的倍数。
×
练习
1. 既是质数又是偶数 ( )
2. 最小的合数( )
3. 7的最大因数( )
4. 最小的质数( )
5. 两个最小质数的和( )
6. 10以内既是奇数又是合数( )
7. 一位数中最大的偶数( )
8. 既不是质数又不是合数( )
这个号码是( )
老师的QQ号码排列如下:
1
2
4
7
2
5
9
8
24725981
练习
(1)如果A=2×3×5,B=2×3×3,A和B的最大公因数是( ),最小公倍数是( )。
填空:
(2)如果A÷B=5(A,B为自然数,B≠0),那么A,B的最大公因数是( ),最小公倍数是( )。
6
90
B
A
练习
5×8=40(分)
答:至少再过40分又同时发车。
23路公交车每5分发车一次,6路公交车每8分发车一次,这两路车同时发车后,至少再过多少时间又同时发车?
练习
有两根木棒,分别长12厘米、44厘米,要把他们截成同样长的小木棒,且没有剩余,每根小木棒最长是多少厘米?
2
2
3 11
12 44
6 22
答:每根小木棒最长4厘米。
2×2=4(厘米)
这节课的复习之后,与复习之前相比你有哪些提升?
