5.1.1相交线 课件(共29张PPT)
图片预览







文档简介
(共29张PPT)
人教版七下第五章相交线与平行线
5.1相交线
人教版七年级下册
重点:邻补角和对顶角的概念及对顶角相等的性质.
难点:根据邻补角和对顶角的概念迅速、准确辨别对顶角和邻补角及对顶角相等的性质和邻补角的综合运用.
教学目标
1.通过动手、操作、推断、交流等活动,进一步发展空间观念,培养识图能力,推理能力和有条理表达能力
2.理解对顶角相等,并能运用它解决一些简单问题.
如果两条直线有一个公共点,就说这两条直线相交,公共点叫做这两条直线的交点.
直线AB、CD相交于点O
A
B
C
D
O
符号语言:
复习回顾
新课引入
如图,一块布片和一把剪刀,剪布时,用力握紧把手,引发了什么变化 进而使什么也发生了变化
如果把剪刀的构造看作两条相交的直线,这就关系到两条相交直线所成的角的问题.
握紧把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小直到剪开布片.
任意画两条相交直线,形成的小于平角的角有几个
四个角
4
3
2
1
新知讲解
思考:图中∠1 和∠2,∠1 和∠3有什么位置关系?
A
B
C
D
∠1 和∠3对顶,它们有一个公共顶点 O,并且∠1 的两边分别是∠3 的两边的反向延长线.
∠1 和∠2 相邻,它们有一条公共边OC,它们的另一边互为反向延长线.
O
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.
邻补角的定义:
新知讲解
如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.
对顶角的定义:
3.另一边互为反向延长线.
归纳
①两条直线相交形成的角;
②有公共顶点;
③没有公共边
一.互为邻补角的三个特征:
1.有一个公共顶点;
2.有一条公共边;
二.对顶角的三个特征:
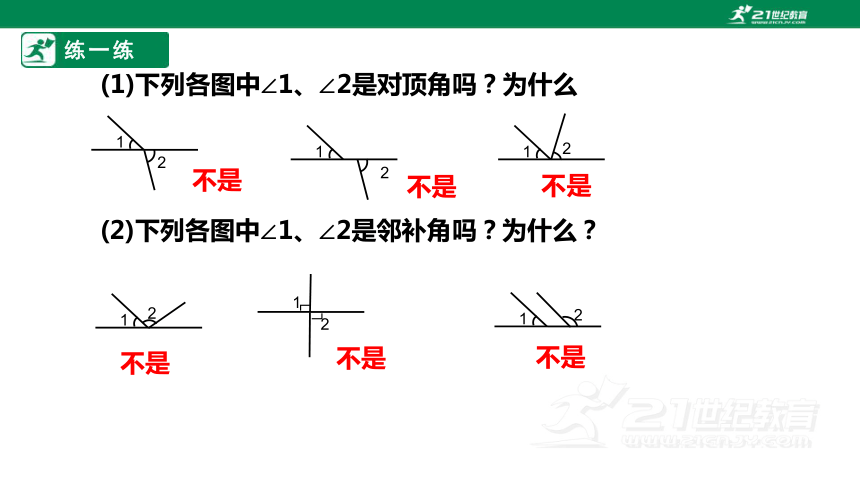
(1)下列各图中∠1、∠2是对顶角吗?为什么
1
2
1
2
1
2
(2)下列各图中∠1、∠2是邻补角吗?为什么?
1
2
1
2
1
2
不是
不是
不是
不是
不是
不是
练一练
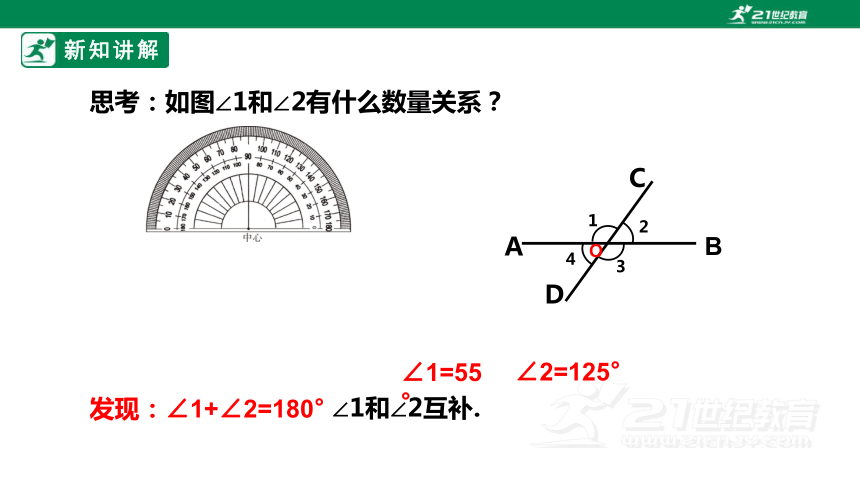
思考:如图∠1和∠2有什么数量关系?
新知讲解
4
3
2
1
A
B
C
D
O
∠1=55°
∠2=125°
发现:∠1+∠2=180°
∠1和∠2互补.
注意:邻补角和补角的区别:邻补角一定互补,但互补的两个角不一定是邻 补角.因为邻补角既相邻又互补,但互补的两个角不管其位置如何,只要它们的和为180°就是一对互补的角.
归纳
思考:如图∠1 和∠3有什么数量关系?
新知讲解
4
3
2
1
A
B
C
D
O
∠1=55°
∠3=125°
发现:∠1=∠3
对顶角相等
对顶角的性质:对顶角相等.
已知:直线AB与CD相交于O点(如图),
求证:∠1=∠3、 ∠2=∠4
)
O
A
B
C
D
(
1
3
4
2
)
(
证明:∵直线AB与CD相交于O点,
∴∠1+∠2=180°、 ∠2+∠3=180°
∴∠1=∠3
同理可得:∠2=∠4
新知讲解
如图所示,三条直线AB、CD、EF相交于一点O,∠AOC的对顶角是 ,∠COF的对顶角是 ,∠COB的邻补角是 .
∠BOD
A
C
B
D
E
F
O
∠DOE
∠AOC和∠BOD
练一练
例1 如图,直线AB、CD相交,∠1=140°,求 ∠2、∠3、∠ 4的度数.
解:由邻补角的定义,可得
∠2=180°-∠1
=180°- 140°
=40°
由对顶角相等,可得
∠3=∠1=140°
∠4=∠2=40°
例题讲解
1
2
3
4
a
b
如图,直线a、b相交,∠1=m°,求 ∠2、∠3、∠ 4的度数.
解:由邻补角的定义,可得
∠2=180°-∠1
=180°- m°
由对顶角相等,可得
∠3=∠1=m°
∠4=∠2=180°- m°
练一练
4
3
2
1
a
b
1
3
4
2
例2 如图,直线a、b相交,若∠1+∠3=50°,求 ∠1、 ∠2、∠3、∠ 4的度数.
解:由图中可得∠1和∠3是对顶角,
∴∠1=∠3
∵ ∠1+∠3=50°,
∴∠1=∠3=25°
由邻补角的定义,可得
∠2=180°-∠1=155°
同理可得∠4=155°
例题讲解
1. 如图,若∠1:∠2=2:7 ,求各角的度数。
解:设∠1=2x°,则∠2=7x °
根据邻补角的定义,得
2x+7x=180°
∠3=40°, ∠4=140°
x=20°
则∠1=40°, ∠2=140°
根据对顶角相等,得
练一练
2. 已知:直线AB、CD、EF相交于O点,OA平分∠EOC,∠EOC=70°,求∠BOD和∠BOC的度数.
=108°-35°=145°(邻补角定义)
A
C
B
D
E
F
解:∵OA平分∠EOC
∠EOC=70°(已知)
∴∠AOC=35°(角平分线定义)
∴∠BOD=∠AOC=35°(对顶角相等)
∴∠BOC=180°-∠AOC
练一练
课堂练习
1. 如图,直线AB , CD相交于点O , 如果∠1=35°,那么∠2的度数是( )
A. 35° B. 55° C. 145° D. 165°
2. 如果同一平面内有三条直线,那么它们交点个数是( )个.
A. 3个 B. 1或3个 C. 1或2或3个 D. 0或1或2或3个
A
D
课堂练习
3. 下列四个图形中,∠1与∠2是对顶角的是( )
1
2
1
2
1
2
1
2
A B C D
4. 若∠AOB=50° , 则∠AOB的对顶角的大小为( )
A. 40° B. 50° C. 130° D. 140°
C
B
课堂练习
5. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,若∠BOD=80°,则∠BOM等于( )
A. 40° B. 80° C. 100° D. 140°
A
6. 一个角的对顶角有 个,邻补角最多有 个,而补角则可以有 个.
7. 右图中∠AOC的对顶角是 ,
∠AOC的邻补角是 .
8. 若∠1与∠3是对顶角,∠1=58 ,则∠3=______;
若∠2与∠4是邻补角,则∠2+∠4 =______.
A
B
C
D
O
∠BOD
∠AOD、
∠BOC
58
180
课堂练习
1
2
无数
9. 若∠1与∠2为对顶角,∠1与∠3互补,则∠2+∠3= .
180
10. 如图,已知直线AB、CD 相交于点O,且∠AOC=80°,OE 把∠BOD 分成两部分,且∠BOE∶∠EOD=2∶3,求∠EOD的度数.
课堂练习
A
C
B
D
O
E
x=16°,
解:
因为 ∠AOC =∠BOD(对顶角相等),且∠AOC=80°.
所以∠BOD=80°.
因为∠BOE∶ ∠EOD=2∶3
所以 可设 ∠BOE =2x, ∠EOD=3k,
2x+3x=80°
所以∠EOD=3×16°=48°.
课堂练习
课堂练习
10. 如图,直线AB和CD相交于点O,若∠BOD=40° , OA平分∠EOC , 求∠EOD的度数.
解:∵∠BOD=40°,
∴∠EOD=180°-∠AOE-∠BOD=180°-40°-40°=100°.
∴∠AOE=∠AOC=40°,
∵OA平分∠EOC,
∴∠AOC=∠BOD=40°.
A
C
B
D
O
E
课堂总结
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.
1.邻补角的定义:
如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.
2.对顶角的定义:
3.对顶角的性质:
对顶角相等.
课外作业
习题5.1
第8页第2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版七下第五章相交线与平行线
5.1相交线
人教版七年级下册
重点:邻补角和对顶角的概念及对顶角相等的性质.
难点:根据邻补角和对顶角的概念迅速、准确辨别对顶角和邻补角及对顶角相等的性质和邻补角的综合运用.
教学目标
1.通过动手、操作、推断、交流等活动,进一步发展空间观念,培养识图能力,推理能力和有条理表达能力
2.理解对顶角相等,并能运用它解决一些简单问题.
如果两条直线有一个公共点,就说这两条直线相交,公共点叫做这两条直线的交点.
直线AB、CD相交于点O
A
B
C
D
O
符号语言:
复习回顾
新课引入
如图,一块布片和一把剪刀,剪布时,用力握紧把手,引发了什么变化 进而使什么也发生了变化
如果把剪刀的构造看作两条相交的直线,这就关系到两条相交直线所成的角的问题.
握紧把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小直到剪开布片.
任意画两条相交直线,形成的小于平角的角有几个
四个角
4
3
2
1
新知讲解
思考:图中∠1 和∠2,∠1 和∠3有什么位置关系?
A
B
C
D
∠1 和∠3对顶,它们有一个公共顶点 O,并且∠1 的两边分别是∠3 的两边的反向延长线.
∠1 和∠2 相邻,它们有一条公共边OC,它们的另一边互为反向延长线.
O
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.
邻补角的定义:
新知讲解
如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.
对顶角的定义:
3.另一边互为反向延长线.
归纳
①两条直线相交形成的角;
②有公共顶点;
③没有公共边
一.互为邻补角的三个特征:
1.有一个公共顶点;
2.有一条公共边;
二.对顶角的三个特征:
(1)下列各图中∠1、∠2是对顶角吗?为什么
1
2
1
2
1
2
(2)下列各图中∠1、∠2是邻补角吗?为什么?
1
2
1
2
1
2
不是
不是
不是
不是
不是
不是
练一练
思考:如图∠1和∠2有什么数量关系?
新知讲解
4
3
2
1
A
B
C
D
O
∠1=55°
∠2=125°
发现:∠1+∠2=180°
∠1和∠2互补.
注意:邻补角和补角的区别:邻补角一定互补,但互补的两个角不一定是邻 补角.因为邻补角既相邻又互补,但互补的两个角不管其位置如何,只要它们的和为180°就是一对互补的角.
归纳
思考:如图∠1 和∠3有什么数量关系?
新知讲解
4
3
2
1
A
B
C
D
O
∠1=55°
∠3=125°
发现:∠1=∠3
对顶角相等
对顶角的性质:对顶角相等.
已知:直线AB与CD相交于O点(如图),
求证:∠1=∠3、 ∠2=∠4
)
O
A
B
C
D
(
1
3
4
2
)
(
证明:∵直线AB与CD相交于O点,
∴∠1+∠2=180°、 ∠2+∠3=180°
∴∠1=∠3
同理可得:∠2=∠4
新知讲解
如图所示,三条直线AB、CD、EF相交于一点O,∠AOC的对顶角是 ,∠COF的对顶角是 ,∠COB的邻补角是 .
∠BOD
A
C
B
D
E
F
O
∠DOE
∠AOC和∠BOD
练一练
例1 如图,直线AB、CD相交,∠1=140°,求 ∠2、∠3、∠ 4的度数.
解:由邻补角的定义,可得
∠2=180°-∠1
=180°- 140°
=40°
由对顶角相等,可得
∠3=∠1=140°
∠4=∠2=40°
例题讲解
1
2
3
4
a
b
如图,直线a、b相交,∠1=m°,求 ∠2、∠3、∠ 4的度数.
解:由邻补角的定义,可得
∠2=180°-∠1
=180°- m°
由对顶角相等,可得
∠3=∠1=m°
∠4=∠2=180°- m°
练一练
4
3
2
1
a
b
1
3
4
2
例2 如图,直线a、b相交,若∠1+∠3=50°,求 ∠1、 ∠2、∠3、∠ 4的度数.
解:由图中可得∠1和∠3是对顶角,
∴∠1=∠3
∵ ∠1+∠3=50°,
∴∠1=∠3=25°
由邻补角的定义,可得
∠2=180°-∠1=155°
同理可得∠4=155°
例题讲解
1. 如图,若∠1:∠2=2:7 ,求各角的度数。
解:设∠1=2x°,则∠2=7x °
根据邻补角的定义,得
2x+7x=180°
∠3=40°, ∠4=140°
x=20°
则∠1=40°, ∠2=140°
根据对顶角相等,得
练一练
2. 已知:直线AB、CD、EF相交于O点,OA平分∠EOC,∠EOC=70°,求∠BOD和∠BOC的度数.
=108°-35°=145°(邻补角定义)
A
C
B
D
E
F
解:∵OA平分∠EOC
∠EOC=70°(已知)
∴∠AOC=35°(角平分线定义)
∴∠BOD=∠AOC=35°(对顶角相等)
∴∠BOC=180°-∠AOC
练一练
课堂练习
1. 如图,直线AB , CD相交于点O , 如果∠1=35°,那么∠2的度数是( )
A. 35° B. 55° C. 145° D. 165°
2. 如果同一平面内有三条直线,那么它们交点个数是( )个.
A. 3个 B. 1或3个 C. 1或2或3个 D. 0或1或2或3个
A
D
课堂练习
3. 下列四个图形中,∠1与∠2是对顶角的是( )
1
2
1
2
1
2
1
2
A B C D
4. 若∠AOB=50° , 则∠AOB的对顶角的大小为( )
A. 40° B. 50° C. 130° D. 140°
C
B
课堂练习
5. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,若∠BOD=80°,则∠BOM等于( )
A. 40° B. 80° C. 100° D. 140°
A
6. 一个角的对顶角有 个,邻补角最多有 个,而补角则可以有 个.
7. 右图中∠AOC的对顶角是 ,
∠AOC的邻补角是 .
8. 若∠1与∠3是对顶角,∠1=58 ,则∠3=______;
若∠2与∠4是邻补角,则∠2+∠4 =______.
A
B
C
D
O
∠BOD
∠AOD、
∠BOC
58
180
课堂练习
1
2
无数
9. 若∠1与∠2为对顶角,∠1与∠3互补,则∠2+∠3= .
180
10. 如图,已知直线AB、CD 相交于点O,且∠AOC=80°,OE 把∠BOD 分成两部分,且∠BOE∶∠EOD=2∶3,求∠EOD的度数.
课堂练习
A
C
B
D
O
E
x=16°,
解:
因为 ∠AOC =∠BOD(对顶角相等),且∠AOC=80°.
所以∠BOD=80°.
因为∠BOE∶ ∠EOD=2∶3
所以 可设 ∠BOE =2x, ∠EOD=3k,
2x+3x=80°
所以∠EOD=3×16°=48°.
课堂练习
课堂练习
10. 如图,直线AB和CD相交于点O,若∠BOD=40° , OA平分∠EOC , 求∠EOD的度数.
解:∵∠BOD=40°,
∴∠EOD=180°-∠AOE-∠BOD=180°-40°-40°=100°.
∴∠AOE=∠AOC=40°,
∵OA平分∠EOC,
∴∠AOC=∠BOD=40°.
A
C
B
D
O
E
课堂总结
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.
1.邻补角的定义:
如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.
2.对顶角的定义:
3.对顶角的性质:
对顶角相等.
课外作业
习题5.1
第8页第2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
