5.1.3 同位角、内错角、同旁内角 课件(共32张PPT)
文档属性
| 名称 | 5.1.3 同位角、内错角、同旁内角 课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-06 12:38:08 | ||
图片预览



文档简介
(共32张PPT)
人教版七下第五章相交线与平行线
5.1.3 同位角、内错角、同旁内角
人教版七年级下册
1.理解同位角、内错角、同旁内角的概念;
2.通过在图形中识别同位角、内错角、同旁内角,提高识图能力,体会分类的思想
教学重点:结合图形识别同位角、内错角、同旁内角.
教学难点:从复杂图形分解为基本图形的过程中,体会化繁为简,化难为易的化归思想.(难点)
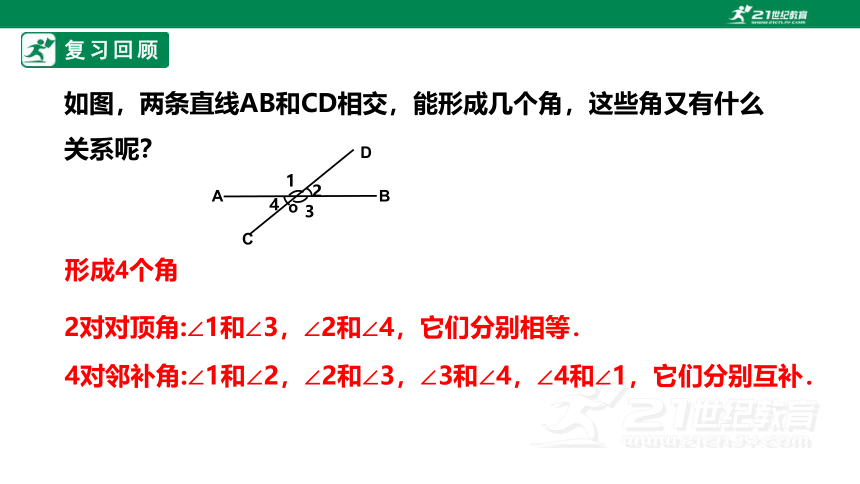
如图,两条直线AB和CD相交,能形成几个角,这些角又有什么关系呢?
2对对顶角:∠1和∠3,∠2和∠4,它们分别相等.
4对邻补角:∠1和∠2,∠2和∠3,∠3和∠4,∠4和∠1,它们分别互补.
A
B
C
D
o
4
3
2
1
形成4个角
复习回顾
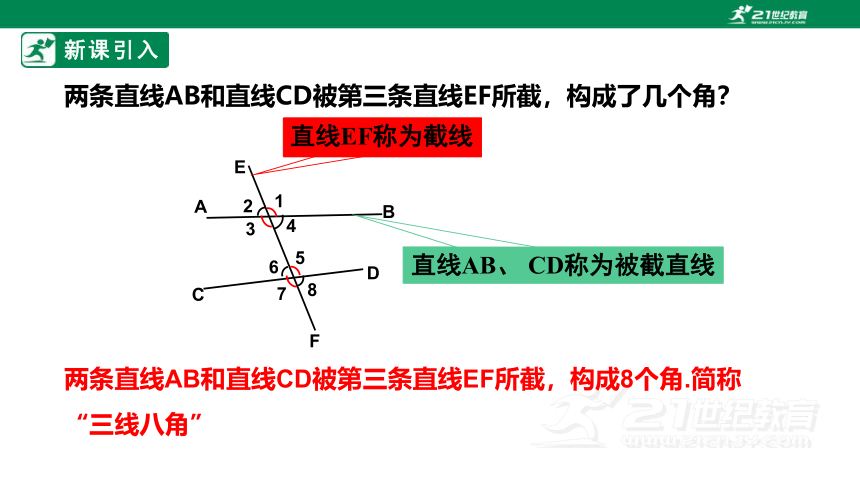
两条直线AB和直线CD被第三条直线EF所截,构成了几个角?
两条直线AB和直线CD被第三条直线EF所截,构成8个角.简称“三线八角”
新课引入
B
C
E
F
D
1
2
3
4
5
8
7
6
A
直线EF称为截线
直线AB、 CD称为被截直线
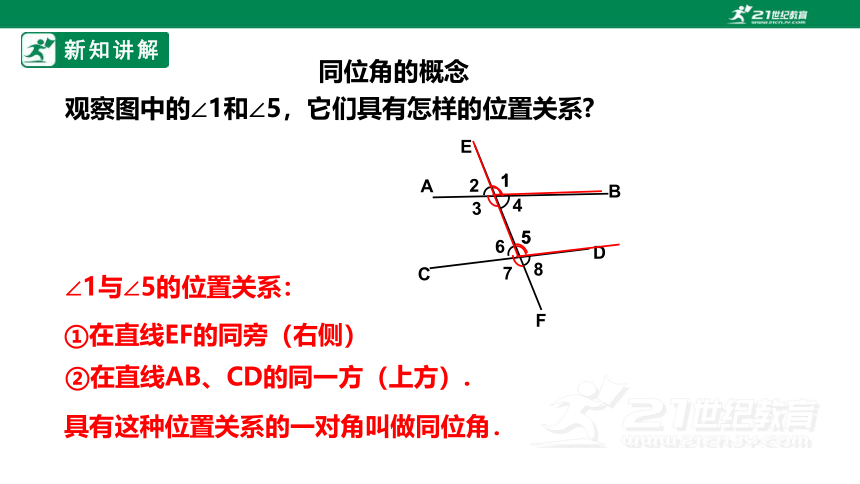
观察图中的∠1和∠5,它们具有怎样的位置关系
同位角的概念
∠1与∠5的位置关系:
①在直线EF的同旁(右侧)
②在直线AB、CD的同一方(上方).
具有这种位置关系的一对角叫做同位角.
新知讲解
B
C
E
F
D
1
2
3
4
5
8
7
6
A
1
5
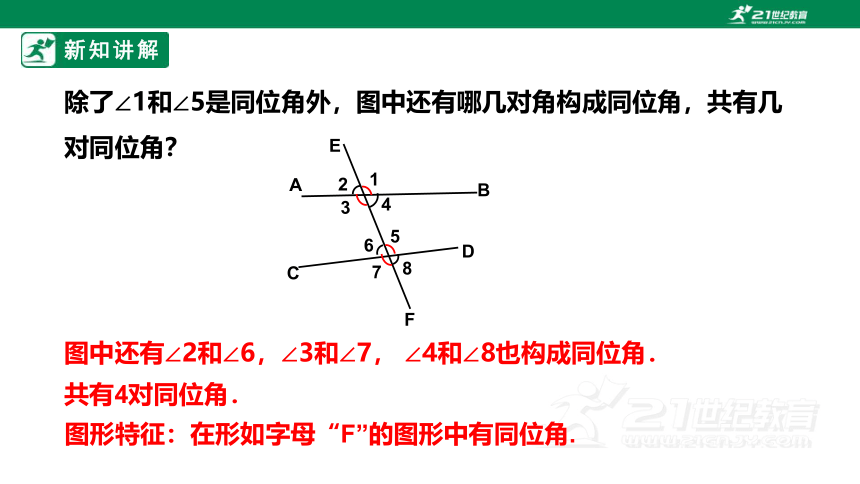
除了∠1和∠5是同位角外,图中还有哪几对角构成同位角,共有几对同位角?
图形特征:在形如字母“F”的图形中有同位角.
图中还有∠2和∠6,∠3和∠7, ∠4和∠8也构成同位角.
共有4对同位角.
新知讲解
B
C
E
F
D
1
2
3
4
5
8
7
6
A
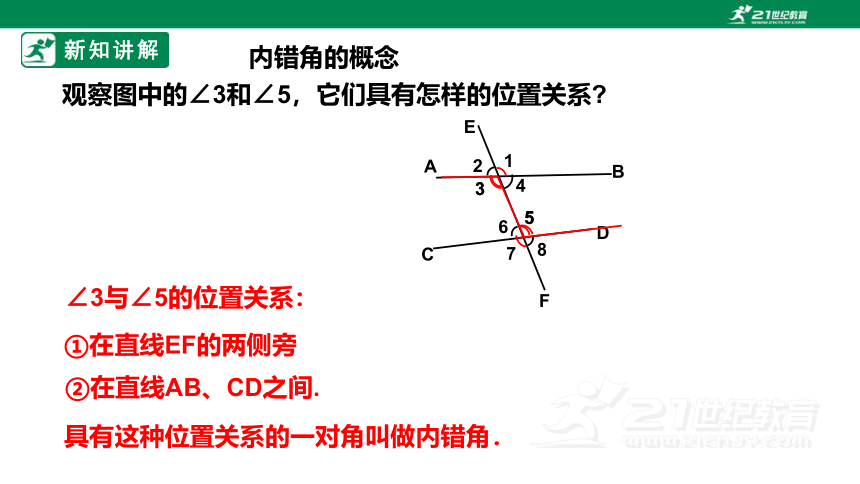
观察图中的∠3和∠5,它们具有怎样的位置关系
内错角的概念
∠3与∠5的位置关系:
①在直线EF的两侧旁
②在直线AB、CD之间.
具有这种位置关系的一对角叫做内错角.
新知讲解
B
C
E
F
D
1
2
3
4
5
8
7
6
A
3
5
除了∠3和∠5是内错角外,图中还有哪几对角构成内错角,共有几对内错角?
图形特征:在形如字母“Z”的图形中有内错角.
内错角:除了∠3和∠5是内错角,还有∠4和∠6.
共有2对内错角.
新知讲解
B
C
E
F
D
1
2
3
4
5
8
7
6
A
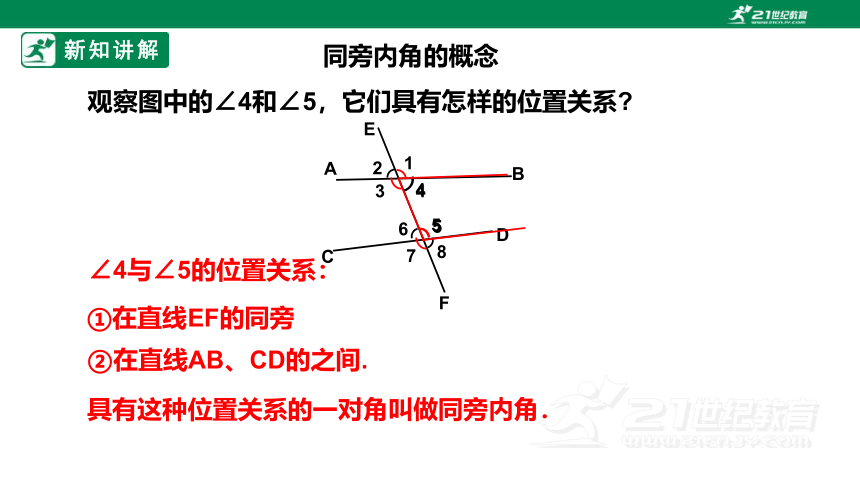
观察图中的∠4和∠5,它们具有怎样的位置关系
同旁内角的概念
∠4与∠5的位置关系:
①在直线EF的同旁
②在直线AB、CD的之间.
具有这种位置关系的一对角叫做同旁内角.
新知讲解
B
C
E
F
D
1
2
3
4
5
8
7
6
A
5
4
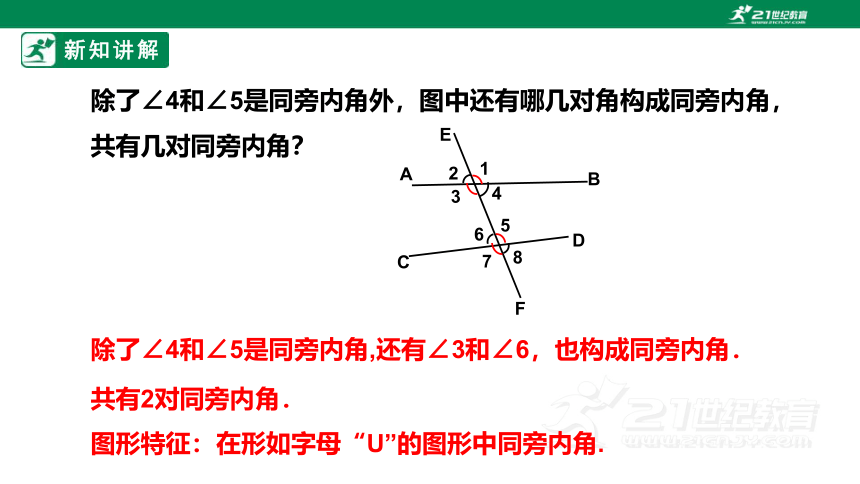
除了∠4和∠5是同旁内角外,图中还有哪几对角构成同旁内角,共有几对同旁内角?
图形特征:在形如字母“U”的图形中同旁内角.
除了∠4和∠5是同旁内角,还有∠3和∠6,也构成同旁内角.
共有2对同旁内角.
新知讲解
B
C
E
F
D
1
2
3
4
5
8
7
6
A
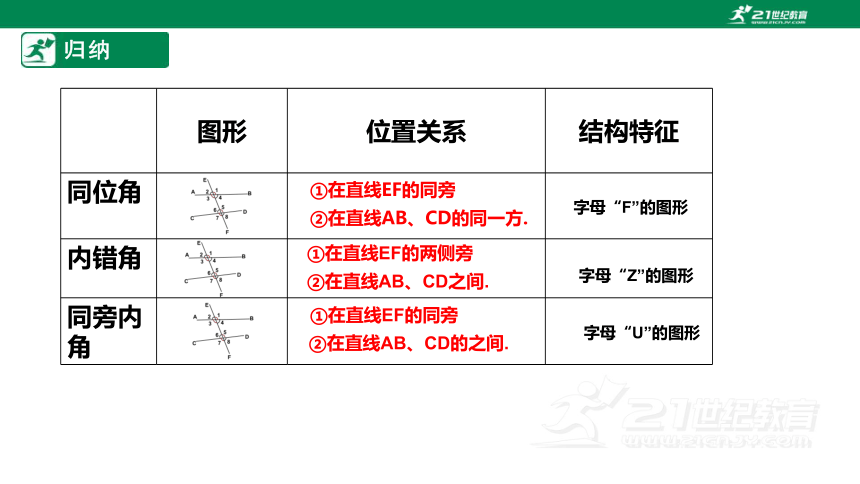
图形 位置关系 结构特征
同位角
内错角
同旁内角
①在直线EF的同旁
②在直线AB、CD的同一方.
字母“F”的图形
①在直线EF的两侧旁
②在直线AB、CD之间.
①在直线EF的同旁
②在直线AB、CD的之间.
字母“Z”的图形
字母“U”的图形
归纳
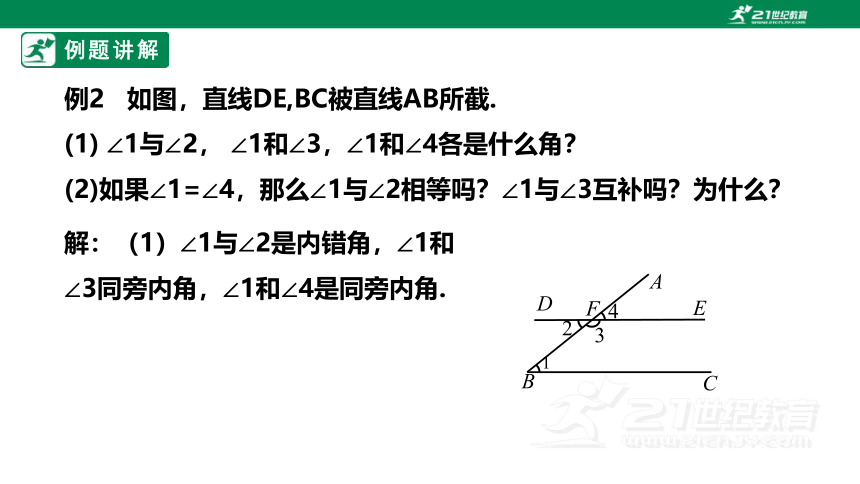
例2 如图,直线DE,BC被直线AB所截.
(1) ∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗?为什么?
解:(1)∠1与∠2是内错角,∠1和∠3同旁内角,∠1和∠4是同旁内角.
4
3
2
1
F
E
D
C
B
A
例题讲解
解:
(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,
那么∠1=∠2.
因为∠3和∠4互补,即∠4+∠3=180°,
又因为∠1=∠4,
所以∠4+∠3=180°,即∠1与∠3互补.
例题讲解
例题讲解
例3如图所示,∠1∽∠8这8个角中,同位角共有多少对?内错角共有多少对?同旁内角共有多少对?
B
C
E
F
D
1
2
3
4
5
8
7
6
A
分析:图中一共有四条直线,图形比较复杂,可以将图形分解成几个简单的基本图形,这样比较容易确定哪两条直线被第三条直线所截,从而既不重复又不遗漏地分辨出所有的同位角、内错角和同旁内角.
例题讲解
可分解为如图所示的三种基本图形.
B
C
E
F
D
1
2
3
4
5
8
7
6
A
M
N
3
4
图1
B
C
D
A
M
N
图2
2
5
8
7
6
B
C
E
F
D
A
图3
2
4
5
8
7
6
C
E
F
D
M
N
例题讲解
图1可看作直线AB,CD被直线MN所截,截得的角∠3与∠4是内错角.
3
4
图1
B
C
D
A
M
N
例题讲解
图2
2
5
8
7
6
B
C
E
F
D
A
图2可看作直线AB,CD被直线EF所截,截得的角,∠2与∠8是同位角∠2与∠6是内错角,∠2与∠5是同旁内角.
例题讲解
图3
2
4
5
8
7
6
C
E
F
D
M
N
图3可看作直线MN,CD被直线EF所截,截得的角,∠2与∠7是同位角,∠2与∠5是内错角,∠2与∠6是同旁内角.
看作直线MN,EF被直线CD所截,截得的角,∠4与∠5是同位角,∠4与∠7是内错角,∠4与∠6是同旁内角.
看作直线CD,EF被直线MN所截,截得的角,∠2与∠4是同旁内角.
例题讲解
综合以上各种情况,同位角有3对,内错角有4 对,同旁内角有4对.
3
4
图1
B
C
D
A
M
N
图2
2
5
8
7
6
B
C
E
F
D
A
图3
2
4
5
8
7
6
C
E
F
D
M
N
课堂练习
1. 如图,下列说法错误的是( )
∠2与∠6是同位角 B. ∠3与∠4是内错角
C. ∠1与∠3是对顶角 D. ∠3与∠5是同旁内角
A
课堂练习
2. 如图,与∠B是同旁内角的角有( )
A. 1个 B. 2个 C. 3个 D. 4个
C
课堂练习
3. 如图,给出下列说法:①∠B和∠1是同位角;②∠1和∠3是对顶角;③∠2和∠4是内错角;④∠A和∠BCD是同旁内角.其中说法正确的有( )
2
1
3
4
B
C
E
D
A
A. 1个 B. 2个 C. 3个 D. 4个
B
课堂练习
4. 如图,按各组角的位置判断错误的是( )
∠1与∠4是同旁内角 B. ∠3与∠4是内错角
C. ∠5与∠6是同旁内角 D. ∠2与∠5是同位角
C
课堂练习
5. 如图,∠ABD与∠BDC是( )形成的内错角
A. 直线AD、BC被直线BD所截 B. 直线AB、CD被直线BD所截
C. 直线AB、CD被直线AC所截 D. 直线AD、BC被直线AC所截
B
课堂练习
6. 如图所标的5个角中,∠1与________是同位角,∠5与________是同旁内角
7. 已知直线a、b被直线c所截,则与∠1是内错角关系的是________.
第6题
1
5
4
3
2
B
C
E
F
D
A
1
2
第7题
B
C
D
A
M
N
3
∠4
∠1
∠2
课堂练习
8. 如图,指出图中直线AC , BC被直线AB所截的同位角、内错角、同旁内角.
解:∵直线AC、BC被直线AB所截,
∴∠1与∠2,∠4与∠DBC是同位角;
∠1与∠3,∠4与∠5是内错角;
∠3与∠4是同旁内角,∠1与∠5是同旁内角.
2
1
3
4
B
C
5
A
课堂练习
9.如图(1)指出直线DC,AB被直线AC所截得的内错角.
(2)指出直线AD,BC被直线AE所截得的同位角.
(3)指出∠ 4 与∠ 7, ∠ 2 与∠ 6,∠ ADC 与∠ DAB是什么位置关系的角,并指出是哪两条线被哪一条线所截得到的.
课堂练习
解: (1) 指出直线DC,AB被直线AC所截得的内错角是∠ 1 与∠ 5.
(2) 指出直线AD,BC被直线AE所截得的同位角是∠ 9 与∠ BAD.
(3) ∠ 4 与∠ 7是直线AC所截得的内错角,∠ 2 与∠ 6是直线AD,BC被直线AC所截得的内错角,∠ ADC 与∠ DAB是直线AB,DC被直线AD所截得的同旁内角
课堂总结
1.两条直线被第三条直线所截而产生的三种角:同位角、内错角、同旁内角.
2.同位角、内错角、同旁内角的结构特征:
同位角 (“F”型)
内错角 (“Z”型)
同旁内角(“U”型)
3. 在图形中判断三线八角的方法:
①判断时应先找到“截线”,再找另外两直线,然后根据角的位置决定是哪一种角;
②当图形复杂时可把暂时不需要的线段、角等遮住,也可采用图形分解法、图形涂色法以排除干扰.
课外作业
习题5.1
第9页第11题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版七下第五章相交线与平行线
5.1.3 同位角、内错角、同旁内角
人教版七年级下册
1.理解同位角、内错角、同旁内角的概念;
2.通过在图形中识别同位角、内错角、同旁内角,提高识图能力,体会分类的思想
教学重点:结合图形识别同位角、内错角、同旁内角.
教学难点:从复杂图形分解为基本图形的过程中,体会化繁为简,化难为易的化归思想.(难点)
如图,两条直线AB和CD相交,能形成几个角,这些角又有什么关系呢?
2对对顶角:∠1和∠3,∠2和∠4,它们分别相等.
4对邻补角:∠1和∠2,∠2和∠3,∠3和∠4,∠4和∠1,它们分别互补.
A
B
C
D
o
4
3
2
1
形成4个角
复习回顾
两条直线AB和直线CD被第三条直线EF所截,构成了几个角?
两条直线AB和直线CD被第三条直线EF所截,构成8个角.简称“三线八角”
新课引入
B
C
E
F
D
1
2
3
4
5
8
7
6
A
直线EF称为截线
直线AB、 CD称为被截直线
观察图中的∠1和∠5,它们具有怎样的位置关系
同位角的概念
∠1与∠5的位置关系:
①在直线EF的同旁(右侧)
②在直线AB、CD的同一方(上方).
具有这种位置关系的一对角叫做同位角.
新知讲解
B
C
E
F
D
1
2
3
4
5
8
7
6
A
1
5
除了∠1和∠5是同位角外,图中还有哪几对角构成同位角,共有几对同位角?
图形特征:在形如字母“F”的图形中有同位角.
图中还有∠2和∠6,∠3和∠7, ∠4和∠8也构成同位角.
共有4对同位角.
新知讲解
B
C
E
F
D
1
2
3
4
5
8
7
6
A
观察图中的∠3和∠5,它们具有怎样的位置关系
内错角的概念
∠3与∠5的位置关系:
①在直线EF的两侧旁
②在直线AB、CD之间.
具有这种位置关系的一对角叫做内错角.
新知讲解
B
C
E
F
D
1
2
3
4
5
8
7
6
A
3
5
除了∠3和∠5是内错角外,图中还有哪几对角构成内错角,共有几对内错角?
图形特征:在形如字母“Z”的图形中有内错角.
内错角:除了∠3和∠5是内错角,还有∠4和∠6.
共有2对内错角.
新知讲解
B
C
E
F
D
1
2
3
4
5
8
7
6
A
观察图中的∠4和∠5,它们具有怎样的位置关系
同旁内角的概念
∠4与∠5的位置关系:
①在直线EF的同旁
②在直线AB、CD的之间.
具有这种位置关系的一对角叫做同旁内角.
新知讲解
B
C
E
F
D
1
2
3
4
5
8
7
6
A
5
4
除了∠4和∠5是同旁内角外,图中还有哪几对角构成同旁内角,共有几对同旁内角?
图形特征:在形如字母“U”的图形中同旁内角.
除了∠4和∠5是同旁内角,还有∠3和∠6,也构成同旁内角.
共有2对同旁内角.
新知讲解
B
C
E
F
D
1
2
3
4
5
8
7
6
A
图形 位置关系 结构特征
同位角
内错角
同旁内角
①在直线EF的同旁
②在直线AB、CD的同一方.
字母“F”的图形
①在直线EF的两侧旁
②在直线AB、CD之间.
①在直线EF的同旁
②在直线AB、CD的之间.
字母“Z”的图形
字母“U”的图形
归纳
例2 如图,直线DE,BC被直线AB所截.
(1) ∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗?为什么?
解:(1)∠1与∠2是内错角,∠1和∠3同旁内角,∠1和∠4是同旁内角.
4
3
2
1
F
E
D
C
B
A
例题讲解
解:
(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,
那么∠1=∠2.
因为∠3和∠4互补,即∠4+∠3=180°,
又因为∠1=∠4,
所以∠4+∠3=180°,即∠1与∠3互补.
例题讲解
例题讲解
例3如图所示,∠1∽∠8这8个角中,同位角共有多少对?内错角共有多少对?同旁内角共有多少对?
B
C
E
F
D
1
2
3
4
5
8
7
6
A
分析:图中一共有四条直线,图形比较复杂,可以将图形分解成几个简单的基本图形,这样比较容易确定哪两条直线被第三条直线所截,从而既不重复又不遗漏地分辨出所有的同位角、内错角和同旁内角.
例题讲解
可分解为如图所示的三种基本图形.
B
C
E
F
D
1
2
3
4
5
8
7
6
A
M
N
3
4
图1
B
C
D
A
M
N
图2
2
5
8
7
6
B
C
E
F
D
A
图3
2
4
5
8
7
6
C
E
F
D
M
N
例题讲解
图1可看作直线AB,CD被直线MN所截,截得的角∠3与∠4是内错角.
3
4
图1
B
C
D
A
M
N
例题讲解
图2
2
5
8
7
6
B
C
E
F
D
A
图2可看作直线AB,CD被直线EF所截,截得的角,∠2与∠8是同位角∠2与∠6是内错角,∠2与∠5是同旁内角.
例题讲解
图3
2
4
5
8
7
6
C
E
F
D
M
N
图3可看作直线MN,CD被直线EF所截,截得的角,∠2与∠7是同位角,∠2与∠5是内错角,∠2与∠6是同旁内角.
看作直线MN,EF被直线CD所截,截得的角,∠4与∠5是同位角,∠4与∠7是内错角,∠4与∠6是同旁内角.
看作直线CD,EF被直线MN所截,截得的角,∠2与∠4是同旁内角.
例题讲解
综合以上各种情况,同位角有3对,内错角有4 对,同旁内角有4对.
3
4
图1
B
C
D
A
M
N
图2
2
5
8
7
6
B
C
E
F
D
A
图3
2
4
5
8
7
6
C
E
F
D
M
N
课堂练习
1. 如图,下列说法错误的是( )
∠2与∠6是同位角 B. ∠3与∠4是内错角
C. ∠1与∠3是对顶角 D. ∠3与∠5是同旁内角
A
课堂练习
2. 如图,与∠B是同旁内角的角有( )
A. 1个 B. 2个 C. 3个 D. 4个
C
课堂练习
3. 如图,给出下列说法:①∠B和∠1是同位角;②∠1和∠3是对顶角;③∠2和∠4是内错角;④∠A和∠BCD是同旁内角.其中说法正确的有( )
2
1
3
4
B
C
E
D
A
A. 1个 B. 2个 C. 3个 D. 4个
B
课堂练习
4. 如图,按各组角的位置判断错误的是( )
∠1与∠4是同旁内角 B. ∠3与∠4是内错角
C. ∠5与∠6是同旁内角 D. ∠2与∠5是同位角
C
课堂练习
5. 如图,∠ABD与∠BDC是( )形成的内错角
A. 直线AD、BC被直线BD所截 B. 直线AB、CD被直线BD所截
C. 直线AB、CD被直线AC所截 D. 直线AD、BC被直线AC所截
B
课堂练习
6. 如图所标的5个角中,∠1与________是同位角,∠5与________是同旁内角
7. 已知直线a、b被直线c所截,则与∠1是内错角关系的是________.
第6题
1
5
4
3
2
B
C
E
F
D
A
1
2
第7题
B
C
D
A
M
N
3
∠4
∠1
∠2
课堂练习
8. 如图,指出图中直线AC , BC被直线AB所截的同位角、内错角、同旁内角.
解:∵直线AC、BC被直线AB所截,
∴∠1与∠2,∠4与∠DBC是同位角;
∠1与∠3,∠4与∠5是内错角;
∠3与∠4是同旁内角,∠1与∠5是同旁内角.
2
1
3
4
B
C
5
A
课堂练习
9.如图(1)指出直线DC,AB被直线AC所截得的内错角.
(2)指出直线AD,BC被直线AE所截得的同位角.
(3)指出∠ 4 与∠ 7, ∠ 2 与∠ 6,∠ ADC 与∠ DAB是什么位置关系的角,并指出是哪两条线被哪一条线所截得到的.
课堂练习
解: (1) 指出直线DC,AB被直线AC所截得的内错角是∠ 1 与∠ 5.
(2) 指出直线AD,BC被直线AE所截得的同位角是∠ 9 与∠ BAD.
(3) ∠ 4 与∠ 7是直线AC所截得的内错角,∠ 2 与∠ 6是直线AD,BC被直线AC所截得的内错角,∠ ADC 与∠ DAB是直线AB,DC被直线AD所截得的同旁内角
课堂总结
1.两条直线被第三条直线所截而产生的三种角:同位角、内错角、同旁内角.
2.同位角、内错角、同旁内角的结构特征:
同位角 (“F”型)
内错角 (“Z”型)
同旁内角(“U”型)
3. 在图形中判断三线八角的方法:
①判断时应先找到“截线”,再找另外两直线,然后根据角的位置决定是哪一种角;
②当图形复杂时可把暂时不需要的线段、角等遮住,也可采用图形分解法、图形涂色法以排除干扰.
课外作业
习题5.1
第9页第11题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
