人教版数学九年级下册 第86课时 解直角三角形的应用(2) 方向角课件(共22张PPT)
文档属性
| 名称 | 人教版数学九年级下册 第86课时 解直角三角形的应用(2) 方向角课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-06 16:27:27 | ||
图片预览







文档简介
(共22张PPT)
第86课时 解直角三角形的应用(2)——方向角
第一部分 新课内容
第二十八章 锐角三角函数
目录
01
知识点导学
02
典型例题
03
变式训练
04
分层训练
方向角一般是以第一个方向为始边向另一个方向旋转相应度数.
注意:描述方向角时,一般先叙述北或南,再叙述偏东或偏西.而几个方向的角平分线按日常习惯描述,即东北,东南,西北,西南.
知识点导学
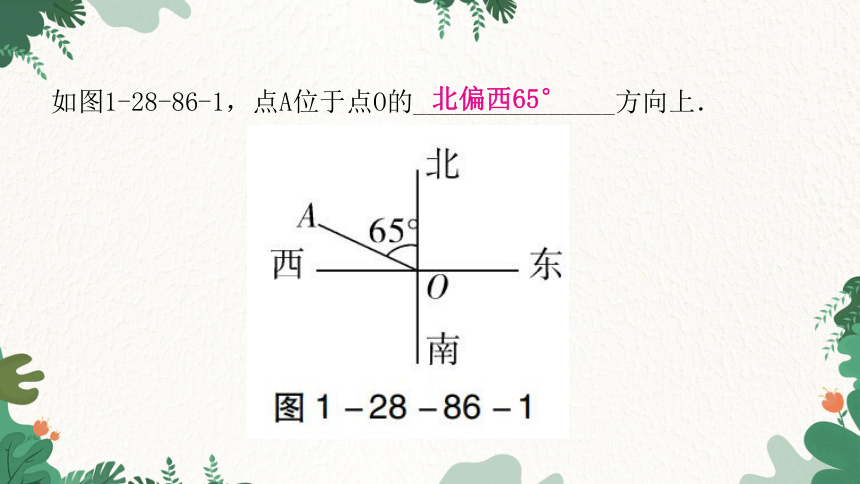
如图1-28-86-1,点A位于点O的_______________方向上.
北偏西65°
知识点1:“一个方向角”类型
典型例题
【例1】如图1-28-86-2,东西两炮台A,B相距2 000 m,它们同时发现入侵舰C,炮台A测得敌舰C在它的南偏东40°方向上,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离分别是多少米(结果精确到1 m)?(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
变式训练
1. 小亮为测量如图1-28-86-3所示的湖面的宽度BC,他在与湖面处在同一水平面上取一点A,测得湖的一端C在A处的正北方向,另一端B在A处的北偏东60°方向上,并测得A,C间的距离为10 m,求湖面的宽度BC.
知识点2:“两个方向角”类型
典型例题
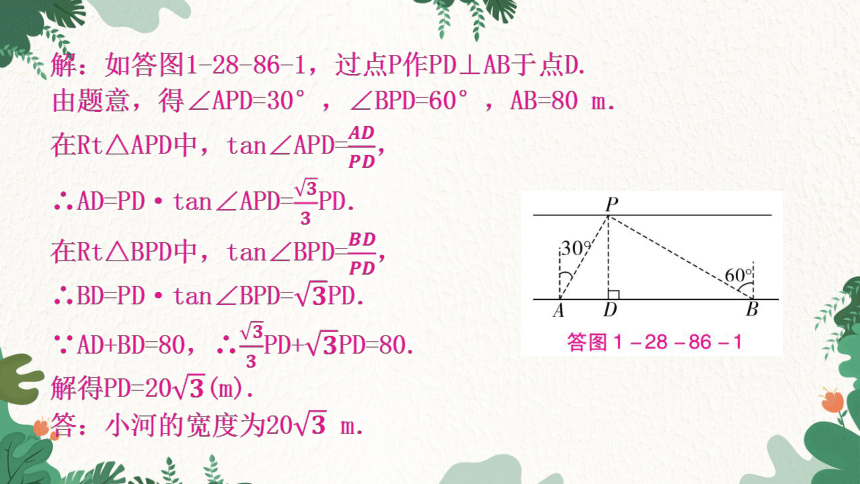
【例2】如图1-28-86-4,某公园中有一条东西走向的小河,河宽固定,小河南岸边上有一块石墩A,北岸边上有一棵大树P,小杨为了测量小河的宽度,他在河的南岸石墩A处测得大树P在其北偏东30°方向上,然后他沿正东方向步行
80 m到达点B处,此时测得大树P在其北
偏西60°方向上.请根据以上所测得的
数据,计算小河的宽度.
变式训练
2. 如图1-28-86-5,小岛A在港口P的南偏西45°方向上,一艘船从港口P出发,沿着正南方向,以12 n mile/h的速度航行,一个半小时后到达B处,在B处测得小岛A在它的南偏西60°方向上.小岛A离港口P有多远?
分层训练
A组
3. 如图1-28-86-6,海面上B,C两岛分别位于A岛的正东和正北方向,A岛与C岛之间的距离约为36 n mile,B岛在C岛的南偏东43°方向上,A,B两岛之间的距离约为
__________n mile(结果精确到0.1 n mile).
(参考数据:sin 43°≈0.68,cos 43°≈
0.73,tan 43°≈0.93)
33.5
4. 如图1-28-86-7,上午8时,一艘船在灯塔A的正北方向的C处,以30 km/h的速度匀速向正东方向航行.如果上午10时它到达灯塔A的北偏东60°的B处,那么A,B之间的距离是__________km(结果保留根号).
B组
5. 如图1-28-86-8,小明同学在东西走向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处正东400 m的B处,测得海中灯塔P在北偏东30°方向上,求灯塔P到环海路的距离.
解:(1)∵∠MAC=60°,∴∠BAC=90°-∠MAC=30°.
∵BP⊥AC,∴∠APB=90°.∴∠ABP=90°-∠BAC=60°.
∵∠CBN=29°,∠ABN=90°,∴∠ABC=∠CBN+∠ABN=119°.
∴∠PBC=∠ABC-∠ABP=59°.
谢 谢
第86课时 解直角三角形的应用(2)——方向角
第一部分 新课内容
第二十八章 锐角三角函数
目录
01
知识点导学
02
典型例题
03
变式训练
04
分层训练
方向角一般是以第一个方向为始边向另一个方向旋转相应度数.
注意:描述方向角时,一般先叙述北或南,再叙述偏东或偏西.而几个方向的角平分线按日常习惯描述,即东北,东南,西北,西南.
知识点导学
如图1-28-86-1,点A位于点O的_______________方向上.
北偏西65°
知识点1:“一个方向角”类型
典型例题
【例1】如图1-28-86-2,东西两炮台A,B相距2 000 m,它们同时发现入侵舰C,炮台A测得敌舰C在它的南偏东40°方向上,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离分别是多少米(结果精确到1 m)?(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
变式训练
1. 小亮为测量如图1-28-86-3所示的湖面的宽度BC,他在与湖面处在同一水平面上取一点A,测得湖的一端C在A处的正北方向,另一端B在A处的北偏东60°方向上,并测得A,C间的距离为10 m,求湖面的宽度BC.
知识点2:“两个方向角”类型
典型例题
【例2】如图1-28-86-4,某公园中有一条东西走向的小河,河宽固定,小河南岸边上有一块石墩A,北岸边上有一棵大树P,小杨为了测量小河的宽度,他在河的南岸石墩A处测得大树P在其北偏东30°方向上,然后他沿正东方向步行
80 m到达点B处,此时测得大树P在其北
偏西60°方向上.请根据以上所测得的
数据,计算小河的宽度.
变式训练
2. 如图1-28-86-5,小岛A在港口P的南偏西45°方向上,一艘船从港口P出发,沿着正南方向,以12 n mile/h的速度航行,一个半小时后到达B处,在B处测得小岛A在它的南偏西60°方向上.小岛A离港口P有多远?
分层训练
A组
3. 如图1-28-86-6,海面上B,C两岛分别位于A岛的正东和正北方向,A岛与C岛之间的距离约为36 n mile,B岛在C岛的南偏东43°方向上,A,B两岛之间的距离约为
__________n mile(结果精确到0.1 n mile).
(参考数据:sin 43°≈0.68,cos 43°≈
0.73,tan 43°≈0.93)
33.5
4. 如图1-28-86-7,上午8时,一艘船在灯塔A的正北方向的C处,以30 km/h的速度匀速向正东方向航行.如果上午10时它到达灯塔A的北偏东60°的B处,那么A,B之间的距离是__________km(结果保留根号).
B组
5. 如图1-28-86-8,小明同学在东西走向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处正东400 m的B处,测得海中灯塔P在北偏东30°方向上,求灯塔P到环海路的距离.
解:(1)∵∠MAC=60°,∴∠BAC=90°-∠MAC=30°.
∵BP⊥AC,∴∠APB=90°.∴∠ABP=90°-∠BAC=60°.
∵∠CBN=29°,∠ABN=90°,∴∠ABC=∠CBN+∠ABN=119°.
∴∠PBC=∠ABC-∠ABP=59°.
谢 谢
