小升初真题特训:立体图形的表面积和体积-小学数学六年级下册苏教版(含答案)
文档属性
| 名称 | 小升初真题特训:立体图形的表面积和体积-小学数学六年级下册苏教版(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-06 19:21:43 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初真题特训:立体图形的表面积和体积(专项突破)-小学数学六年级下册苏教版
一.选择题(共6小题)
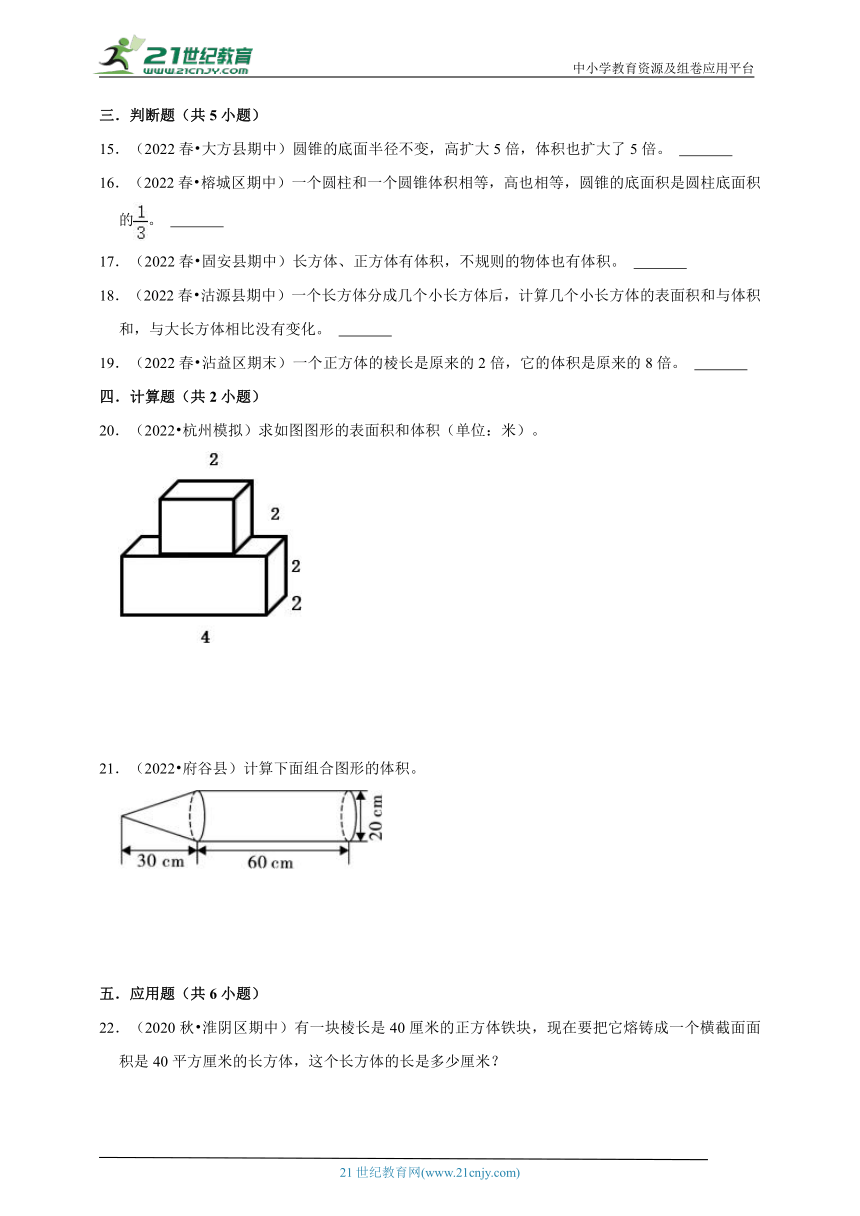
1.(2022春 滑县期中)如图的物体中,( )的体积最大,( )的体积最小。
A.④;① B.④;② C.①;② D.②;④
2.(2022春 城中区期中)把一个长方体木块(如图,单位:dm),削成一个体积最大的圆柱。求这个圆
柱体积的算式是( )
A.3.14×()2×8 B.3.14×()2×8
C.3.14×()2×4 D.3.14×()2×6
3.(2022春 关岭县期末)一个长方体的底面积是2dm2,如果高增加10cm,那么它的体积就会增加( )
A.0.2dm3 B.20dm3 C.20cm3 D.2000cm3
4.(2022春 沽源县期中)如图所示,圆锥形容器中装有4L水,水面高度正好是圆锥高度的一半,已知水面半径和容器口半径的比为1:2,则这个容器还能装( )升水。
A.28 B.32 C.16 D.20
5.(2022春 沽源县期中)淘气和笑笑用同样大小的一块橡皮泥捏图形,淘气捏了一个圆柱体,笑笑捏了一个同样高的圆锥。下面说法正确的有( )个。
①橡皮泥的表面积没变
②橡皮泥的体积没变
③圆柱底面积是圆锥的3倍
④圆柱和圆锥底面半径的比是1:3
A.4 B.3 C.2 D.1
6.(2022春 榕城区期中)把一块底面直径是12厘米,高是9厘米的圆锥形木块沿高切成形状、大小完全相同的两块木块后,表面积比原来增加( )平方厘米。
A.56.52 B.108 C.54 D.113.04
二.填空题(共8小题)
7.(2022秋 莱山区期末)一个长方体的长是11厘米,宽是9厘米,高是10厘米,它的棱长之和是 厘米,体积是 立方厘米。
8.(2022春 长兴县期中)一个圆柱形水桶的容积是40L;水桶的底面积是5dm2。如果装了桶水,那么水面离水桶口的距离还有 dm。
9.(2022春 沂南县期中)一个圆柱体的底面直径4分米,高6分米,它的表面积是 平方分米,它的体积是 立方分米。
10.(2022 潍城区)两个大小相同的量杯中,都盛有450mL的水。将等底等高的圆柱形零件与圆锥形零件分别放入两个量杯中,甲水面的刻度如图所示,则乙水面的刻度应显示 mL。
11.(2022春 中山区期末)一个长方体容器的底面是边长30厘米的正方形,高是50厘米,它的容积是 升。(容器壁的厚度忽略不计)
12.(2022春 城阳区期末)有一根长20分米的长方体木料,将它截成3段后,表面积增加36平方分米,原来这根木料的体积是 立方分米。
13.(2022春 关岭县期末)一根长5m的长方体木料,横截面是一个边长为1dm的正方形。这根木料的横截面的面积是 m2,体积是 m3。
14.(2022春 郧阳区期中)一个长方体,高增加4cm后就变成了一个棱长10cm的正方体(如图),表面积增加了 cm2,体积增加了 cm3。
三.判断题(共5小题)
15.(2022春 大方县期中)圆锥的底面半径不变,高扩大5倍,体积也扩大了5倍。
16.(2022春 榕城区期中)一个圆柱和一个圆锥体积相等,高也相等,圆锥的底面积是圆柱底面积的。
17.(2022春 固安县期中)长方体、正方体有体积,不规则的物体也有体积。
18.(2022春 沽源县期中)一个长方体分成几个小长方体后,计算几个小长方体的表面积和与体积和,与大长方体相比没有变化。
19.(2022春 沾益区期末)一个正方体的棱长是原来的2倍,它的体积是原来的8倍。
四.计算题(共2小题)
20.(2022 杭州模拟)求如图图形的表面积和体积(单位:米)。
21.(2022 府谷县)计算下面组合图形的体积。
五.应用题(共6小题)
22.(2020秋 淮阴区期中)有一块棱长是40厘米的正方体铁块,现在要把它熔铸成一个横截面面积是40平方厘米的长方体,这个长方体的长是多少厘米?
23.(2021春 交口县期末)一间教室长8m,宽5m,高3m,要粉刷教室的屋顶和四周墙壁(除去门窗和黑板的面积29.6m2),如果粉刷一平方米需要10元,粉刷整个教室需要多少元?
24.(2022春 城阳区期末)小东想测量一个石块的体积,他把石块放进一个棱长是3分米的正方体水缸内。石块完全没入水中,水面升高到12厘米,水缸内原有10升水。请你帮小东算一下,这个石块的体积是多少立方分米?
25.(2022春 沂南县期中)将一块不规则的石块全部浸没在长8dm,宽5dm装有水的长方体容器里,测得水面升高5cm。这块石块的体积是多少?
26.(2022春 沽源县期中)一个皮球掉进盛有水的圆柱形玻璃缸内,从里面量,玻璃缸的底面直径是20cm,皮球有的部分浸没在水中。若把皮球从水中取出,则缸内水面下降2cm,求皮球的体积。
27.(2022春 招远市期末)在一个底面半径是10厘米的圆柱形杯中装有水,水里浸没一个底面半径是5厘米的圆锥形铅锤。当铅锤取出时,水面下降了2厘米。
(1)铅锤的体积是多少立方厘米?
(2)铅锤的高是多少厘米?(用方程解答)
小升初真题特训:立体图形的表面积和体积(专项突破)-小学数学六年级下册苏教版
参考答案与试题解析
一.选择题(共6小题)
1.【解答】解:①π×(2r)2h
=π×4r2h
=4πr2h
②π×r2×2h=2πr2h
③×π×(3r)2h
=×π×9r2h
=3πr2h
④π×(2r)2×2h﹣×π×(2r)2×h
=π×4r2×2h﹣πr2h
=6πr2h
6πr2h>4πr2h>3πr2h>2πr2h
所以④的体积最大,②的体积最小。
故选:B。
2.【解答】解:圆柱的底面直径为6分米,高为4分米,体积是:
3.14×()2×4
=3.14×9×4
=113.04(立方分米)
答:削成的圆柱的体积为113.04立方分米。
故选:C。
3.【解答】解:10cm=1dm
2×1=2(dm3)
2dm3=2000cm3
所以,长方体的体积增加2000cm3。
故选:D。
4.【解答】解:设圆锥容器的底面半径为r,则水面半径为,圆锥容器的高为h,水面的高为,
水的体积与圆锥容器容积的比是:
[()2()]:πr2h
=πr2h:πr2h
=1:8
4÷﹣4
=4×8﹣4
=32﹣4
=28(升)
答:这个容器还能装28升水。
故选:A。
5.【解答】解:①根据圆柱、圆锥表面积的意义,圆柱的表面积是指圆柱的侧面加上两个底面的总面积;圆锥的表面积是指圆锥的侧面加上一个底面的总面积,所以他们所捏成的圆柱和圆锥的表面积不同;因此,橡皮泥的表面积没变,这种说法是错误的。
②这块橡皮泥无论捏成什么形状,体积不变,此说法正确。
③因为橡皮泥的体积一定,已知淘气捏成一个圆柱体与笑笑捏成圆锥体同样高,那么圆锥的底面积是圆柱底面积的3倍;因此,圆柱是圆锥底面积的3倍,这种说法是错误的。
④因为圆柱和圆锥的体积相等,高相等,所以圆柱的底面积是圆锥底面积的,根据圆的面积公式:S=πr2,圆柱的底面积与圆锥底面积是比是1:3,圆柱与圆锥底面半径的比是1:3,这种说法是错误的。
故选:D。
6.【解答】解:12×9÷2×2
=108÷2×2
=108(平方厘米)
答:表面积比原来增加108平方厘米。
故选:B。
二.填空题(共8小题)
7.【解答】解:(1)(11+9+10)×4
=30×4
=120(厘米)
(2)11×9×10
=99×10
=990(立方厘米)
答:棱长之和是120厘米,体积是990立方厘米。
故答案为:120;990。
8.【解答】解:40L=40(dm)3
40×÷5
=30÷5
=6(dm)
40÷5=8(dm)
8﹣6=2(dm)
答:水面离水桶口的距离还有 2dm。
故答案为:2。
9.【解答】解:表面积:3.14×(4÷2)2×2+3.14×4×6
=3.14×8+3.14×24
=3.14×32
=100.48(平方分米)
体积:3.14×(4÷2)2×6
=3.14×24
=75.36(立方分米)
答:它的表面积是100.48平方分米;它的体积是75.36立方分米。
故答案为:100.48,75.36。
10.【解答】解:450+(600﹣450)×
=450+150×
=450+50
=500(毫升)
答:乙水面的刻度应显示500毫升。
故答案为:500。
11.【解答】解:30×30×50
=900×50
=45000(立方厘米)
45000立方厘米=45升
答:它的容积是45升。
故答案为:45。
12.【解答】解:(3﹣1)×2
=2×2
=4(个)
36÷4×20
=9×20
=180(立方分米)
答:原来这根木料的体积是180立方分米。
故答案为:180。
13.【解答】解:1dm=0.1m
0.1×0.1=0.01(m2)
0.01×5=0.05(m3)
答:这根木料的横截面的面积是0.01m2,体积是0.05m3。
故答案为:0.01;0.05。
14.【解答】解:10×4×4=160(平方厘米)
10×10×4=400(立方厘米)
答:表面积增加了160平方厘米,体积增加了400立方厘米。
故答案为:160;400。
三.判断题(共5小题)
15.【解答】解:圆柱的体积=πr2h
由此根据积的变化规律可得:r不变,h扩大5倍,πr2h的积就会扩大5倍,
5πr2h÷πr2h=5
所以原题说法正确。
故答案为:√。
16.【解答】解:圆柱和圆锥的高相等体积也相等,圆锥的底面积是圆柱底面积的3倍。
因此题干中的结论是错误的。
故答案为:×。
17.【解答】解:根据分析可知,长方体、正方体有体积,不规则的物体也有体积。此说法是正确的。
故答案为:√。
18.【解答】解:把一个长方体分成几个小长方体后,这几个小长方体的表面积和大于原来长方体的表面积,这几个小长方体的体积和等于原来长方体的体积。
因此题干中的结论是错误的。
故答案为:×。
19.【解答】解:根据正方体的体积公式v=a3,
一个正方体的棱长是原来的2倍,它的体积是原来的2×2×2=8倍。
故答案为:√。
四.计算题(共2小题)
20.【解答】解:(1)正方体4个面的面积:
2×2×4
=4×4
=16(平方米)
长方体的表面积:
(4×2+4×2+2×2)×2
=(8+8+4)×2
=20×2
=40(平方米)
组合图形的表面积:
16+40=56(平方米)
(2)正方体的体积:
2×2×2
=4×2
=8(立方米)
长方体的体积:
4×2×2
=8×2
=16(立方米)
组合图形的体积:
8+16=24(立方米)
21.【解答】解:3.14×(20÷2)2×60+3.14×(20÷2)2×30÷3
=3.14×(6000+1000)
=21980(cm3)
答:组合图形的体积是21980cm3。
五.应用题(共6小题)
22.【解答】解:40×40×40÷40
=64000÷40
=1600(厘米)
答:这个长方体的长是1600厘米。
23.【解答】解:8×5+8×3×2+5×3×2﹣29.6
=40+48+30﹣29.6
=118﹣29.6
=88.4(平方米)
88.4×10=884(元)
答:粉刷整个教室需要884元。
24.【解答】解:10升=10立方分米
12厘米=1.2分米
3×3×1.2﹣10
=10.8﹣10
=0.8(立方分米)
答:这个石块的体积是0.8立方分米。
25.【解答】解:5厘米=0.5分米
8×5×0.5=20(立方分米)
答:这块石块的体积是20立方分米。
26.【解答】解:3.14×(20÷2)2×2÷
=3.14×100×2×
=314×2.5
=785(立方厘米)
答:皮球的体积是785立方厘米。
27.【解答】解:(1)3.14×102×2
=3.14×200
=628(立方厘米)
答:铅锤的体积是628立方厘米。
(2)设铅锤的高是x厘米。
×(3.14×52)×x=628
78.5x=628×3
x=24
答:这个铅锤的高是24厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初真题特训:立体图形的表面积和体积(专项突破)-小学数学六年级下册苏教版
一.选择题(共6小题)
1.(2022春 滑县期中)如图的物体中,( )的体积最大,( )的体积最小。
A.④;① B.④;② C.①;② D.②;④
2.(2022春 城中区期中)把一个长方体木块(如图,单位:dm),削成一个体积最大的圆柱。求这个圆
柱体积的算式是( )
A.3.14×()2×8 B.3.14×()2×8
C.3.14×()2×4 D.3.14×()2×6
3.(2022春 关岭县期末)一个长方体的底面积是2dm2,如果高增加10cm,那么它的体积就会增加( )
A.0.2dm3 B.20dm3 C.20cm3 D.2000cm3
4.(2022春 沽源县期中)如图所示,圆锥形容器中装有4L水,水面高度正好是圆锥高度的一半,已知水面半径和容器口半径的比为1:2,则这个容器还能装( )升水。
A.28 B.32 C.16 D.20
5.(2022春 沽源县期中)淘气和笑笑用同样大小的一块橡皮泥捏图形,淘气捏了一个圆柱体,笑笑捏了一个同样高的圆锥。下面说法正确的有( )个。
①橡皮泥的表面积没变
②橡皮泥的体积没变
③圆柱底面积是圆锥的3倍
④圆柱和圆锥底面半径的比是1:3
A.4 B.3 C.2 D.1
6.(2022春 榕城区期中)把一块底面直径是12厘米,高是9厘米的圆锥形木块沿高切成形状、大小完全相同的两块木块后,表面积比原来增加( )平方厘米。
A.56.52 B.108 C.54 D.113.04
二.填空题(共8小题)
7.(2022秋 莱山区期末)一个长方体的长是11厘米,宽是9厘米,高是10厘米,它的棱长之和是 厘米,体积是 立方厘米。
8.(2022春 长兴县期中)一个圆柱形水桶的容积是40L;水桶的底面积是5dm2。如果装了桶水,那么水面离水桶口的距离还有 dm。
9.(2022春 沂南县期中)一个圆柱体的底面直径4分米,高6分米,它的表面积是 平方分米,它的体积是 立方分米。
10.(2022 潍城区)两个大小相同的量杯中,都盛有450mL的水。将等底等高的圆柱形零件与圆锥形零件分别放入两个量杯中,甲水面的刻度如图所示,则乙水面的刻度应显示 mL。
11.(2022春 中山区期末)一个长方体容器的底面是边长30厘米的正方形,高是50厘米,它的容积是 升。(容器壁的厚度忽略不计)
12.(2022春 城阳区期末)有一根长20分米的长方体木料,将它截成3段后,表面积增加36平方分米,原来这根木料的体积是 立方分米。
13.(2022春 关岭县期末)一根长5m的长方体木料,横截面是一个边长为1dm的正方形。这根木料的横截面的面积是 m2,体积是 m3。
14.(2022春 郧阳区期中)一个长方体,高增加4cm后就变成了一个棱长10cm的正方体(如图),表面积增加了 cm2,体积增加了 cm3。
三.判断题(共5小题)
15.(2022春 大方县期中)圆锥的底面半径不变,高扩大5倍,体积也扩大了5倍。
16.(2022春 榕城区期中)一个圆柱和一个圆锥体积相等,高也相等,圆锥的底面积是圆柱底面积的。
17.(2022春 固安县期中)长方体、正方体有体积,不规则的物体也有体积。
18.(2022春 沽源县期中)一个长方体分成几个小长方体后,计算几个小长方体的表面积和与体积和,与大长方体相比没有变化。
19.(2022春 沾益区期末)一个正方体的棱长是原来的2倍,它的体积是原来的8倍。
四.计算题(共2小题)
20.(2022 杭州模拟)求如图图形的表面积和体积(单位:米)。
21.(2022 府谷县)计算下面组合图形的体积。
五.应用题(共6小题)
22.(2020秋 淮阴区期中)有一块棱长是40厘米的正方体铁块,现在要把它熔铸成一个横截面面积是40平方厘米的长方体,这个长方体的长是多少厘米?
23.(2021春 交口县期末)一间教室长8m,宽5m,高3m,要粉刷教室的屋顶和四周墙壁(除去门窗和黑板的面积29.6m2),如果粉刷一平方米需要10元,粉刷整个教室需要多少元?
24.(2022春 城阳区期末)小东想测量一个石块的体积,他把石块放进一个棱长是3分米的正方体水缸内。石块完全没入水中,水面升高到12厘米,水缸内原有10升水。请你帮小东算一下,这个石块的体积是多少立方分米?
25.(2022春 沂南县期中)将一块不规则的石块全部浸没在长8dm,宽5dm装有水的长方体容器里,测得水面升高5cm。这块石块的体积是多少?
26.(2022春 沽源县期中)一个皮球掉进盛有水的圆柱形玻璃缸内,从里面量,玻璃缸的底面直径是20cm,皮球有的部分浸没在水中。若把皮球从水中取出,则缸内水面下降2cm,求皮球的体积。
27.(2022春 招远市期末)在一个底面半径是10厘米的圆柱形杯中装有水,水里浸没一个底面半径是5厘米的圆锥形铅锤。当铅锤取出时,水面下降了2厘米。
(1)铅锤的体积是多少立方厘米?
(2)铅锤的高是多少厘米?(用方程解答)
小升初真题特训:立体图形的表面积和体积(专项突破)-小学数学六年级下册苏教版
参考答案与试题解析
一.选择题(共6小题)
1.【解答】解:①π×(2r)2h
=π×4r2h
=4πr2h
②π×r2×2h=2πr2h
③×π×(3r)2h
=×π×9r2h
=3πr2h
④π×(2r)2×2h﹣×π×(2r)2×h
=π×4r2×2h﹣πr2h
=6πr2h
6πr2h>4πr2h>3πr2h>2πr2h
所以④的体积最大,②的体积最小。
故选:B。
2.【解答】解:圆柱的底面直径为6分米,高为4分米,体积是:
3.14×()2×4
=3.14×9×4
=113.04(立方分米)
答:削成的圆柱的体积为113.04立方分米。
故选:C。
3.【解答】解:10cm=1dm
2×1=2(dm3)
2dm3=2000cm3
所以,长方体的体积增加2000cm3。
故选:D。
4.【解答】解:设圆锥容器的底面半径为r,则水面半径为,圆锥容器的高为h,水面的高为,
水的体积与圆锥容器容积的比是:
[()2()]:πr2h
=πr2h:πr2h
=1:8
4÷﹣4
=4×8﹣4
=32﹣4
=28(升)
答:这个容器还能装28升水。
故选:A。
5.【解答】解:①根据圆柱、圆锥表面积的意义,圆柱的表面积是指圆柱的侧面加上两个底面的总面积;圆锥的表面积是指圆锥的侧面加上一个底面的总面积,所以他们所捏成的圆柱和圆锥的表面积不同;因此,橡皮泥的表面积没变,这种说法是错误的。
②这块橡皮泥无论捏成什么形状,体积不变,此说法正确。
③因为橡皮泥的体积一定,已知淘气捏成一个圆柱体与笑笑捏成圆锥体同样高,那么圆锥的底面积是圆柱底面积的3倍;因此,圆柱是圆锥底面积的3倍,这种说法是错误的。
④因为圆柱和圆锥的体积相等,高相等,所以圆柱的底面积是圆锥底面积的,根据圆的面积公式:S=πr2,圆柱的底面积与圆锥底面积是比是1:3,圆柱与圆锥底面半径的比是1:3,这种说法是错误的。
故选:D。
6.【解答】解:12×9÷2×2
=108÷2×2
=108(平方厘米)
答:表面积比原来增加108平方厘米。
故选:B。
二.填空题(共8小题)
7.【解答】解:(1)(11+9+10)×4
=30×4
=120(厘米)
(2)11×9×10
=99×10
=990(立方厘米)
答:棱长之和是120厘米,体积是990立方厘米。
故答案为:120;990。
8.【解答】解:40L=40(dm)3
40×÷5
=30÷5
=6(dm)
40÷5=8(dm)
8﹣6=2(dm)
答:水面离水桶口的距离还有 2dm。
故答案为:2。
9.【解答】解:表面积:3.14×(4÷2)2×2+3.14×4×6
=3.14×8+3.14×24
=3.14×32
=100.48(平方分米)
体积:3.14×(4÷2)2×6
=3.14×24
=75.36(立方分米)
答:它的表面积是100.48平方分米;它的体积是75.36立方分米。
故答案为:100.48,75.36。
10.【解答】解:450+(600﹣450)×
=450+150×
=450+50
=500(毫升)
答:乙水面的刻度应显示500毫升。
故答案为:500。
11.【解答】解:30×30×50
=900×50
=45000(立方厘米)
45000立方厘米=45升
答:它的容积是45升。
故答案为:45。
12.【解答】解:(3﹣1)×2
=2×2
=4(个)
36÷4×20
=9×20
=180(立方分米)
答:原来这根木料的体积是180立方分米。
故答案为:180。
13.【解答】解:1dm=0.1m
0.1×0.1=0.01(m2)
0.01×5=0.05(m3)
答:这根木料的横截面的面积是0.01m2,体积是0.05m3。
故答案为:0.01;0.05。
14.【解答】解:10×4×4=160(平方厘米)
10×10×4=400(立方厘米)
答:表面积增加了160平方厘米,体积增加了400立方厘米。
故答案为:160;400。
三.判断题(共5小题)
15.【解答】解:圆柱的体积=πr2h
由此根据积的变化规律可得:r不变,h扩大5倍,πr2h的积就会扩大5倍,
5πr2h÷πr2h=5
所以原题说法正确。
故答案为:√。
16.【解答】解:圆柱和圆锥的高相等体积也相等,圆锥的底面积是圆柱底面积的3倍。
因此题干中的结论是错误的。
故答案为:×。
17.【解答】解:根据分析可知,长方体、正方体有体积,不规则的物体也有体积。此说法是正确的。
故答案为:√。
18.【解答】解:把一个长方体分成几个小长方体后,这几个小长方体的表面积和大于原来长方体的表面积,这几个小长方体的体积和等于原来长方体的体积。
因此题干中的结论是错误的。
故答案为:×。
19.【解答】解:根据正方体的体积公式v=a3,
一个正方体的棱长是原来的2倍,它的体积是原来的2×2×2=8倍。
故答案为:√。
四.计算题(共2小题)
20.【解答】解:(1)正方体4个面的面积:
2×2×4
=4×4
=16(平方米)
长方体的表面积:
(4×2+4×2+2×2)×2
=(8+8+4)×2
=20×2
=40(平方米)
组合图形的表面积:
16+40=56(平方米)
(2)正方体的体积:
2×2×2
=4×2
=8(立方米)
长方体的体积:
4×2×2
=8×2
=16(立方米)
组合图形的体积:
8+16=24(立方米)
21.【解答】解:3.14×(20÷2)2×60+3.14×(20÷2)2×30÷3
=3.14×(6000+1000)
=21980(cm3)
答:组合图形的体积是21980cm3。
五.应用题(共6小题)
22.【解答】解:40×40×40÷40
=64000÷40
=1600(厘米)
答:这个长方体的长是1600厘米。
23.【解答】解:8×5+8×3×2+5×3×2﹣29.6
=40+48+30﹣29.6
=118﹣29.6
=88.4(平方米)
88.4×10=884(元)
答:粉刷整个教室需要884元。
24.【解答】解:10升=10立方分米
12厘米=1.2分米
3×3×1.2﹣10
=10.8﹣10
=0.8(立方分米)
答:这个石块的体积是0.8立方分米。
25.【解答】解:5厘米=0.5分米
8×5×0.5=20(立方分米)
答:这块石块的体积是20立方分米。
26.【解答】解:3.14×(20÷2)2×2÷
=3.14×100×2×
=314×2.5
=785(立方厘米)
答:皮球的体积是785立方厘米。
27.【解答】解:(1)3.14×102×2
=3.14×200
=628(立方厘米)
答:铅锤的体积是628立方厘米。
(2)设铅锤的高是x厘米。
×(3.14×52)×x=628
78.5x=628×3
x=24
答:这个铅锤的高是24厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
