5.6二次函数的图象和性质
图片预览







文档简介
课件27张PPT。初中数学青岛版九年级下
君子耻其言而过其行5.6二次函数图象和性质(3)二次函数y=ax2+bx+c的图象和性质 二次函数y=3(x-1)2+2的图象是由
向 平移 单位,再向 平移 单
位得到的;它的开口 ,对称轴是 ,
顶点坐标是 ,复习y=3(x-1)2+2
=3x2-6x+5你能说出y=3x2-6x+5的图像的对
称轴和顶点坐标吗?y=3x2-6x+5
=3(x-1)2+2怎样直接作出函数y=3x2-6x+5的图象?函数y=ax2+bx+c的图象 我们知道,作出二次函数y=3x2的图象,通过平移抛物线y=3x2可以得到二次函数y=3x2-6x+5的图象. 1.配方:提取二次项系数配方:加上再减去一次项系数绝对值一半的平方整理:前三项化为平方形式,后两项合并同类项化简:去掉中括号老师提示:
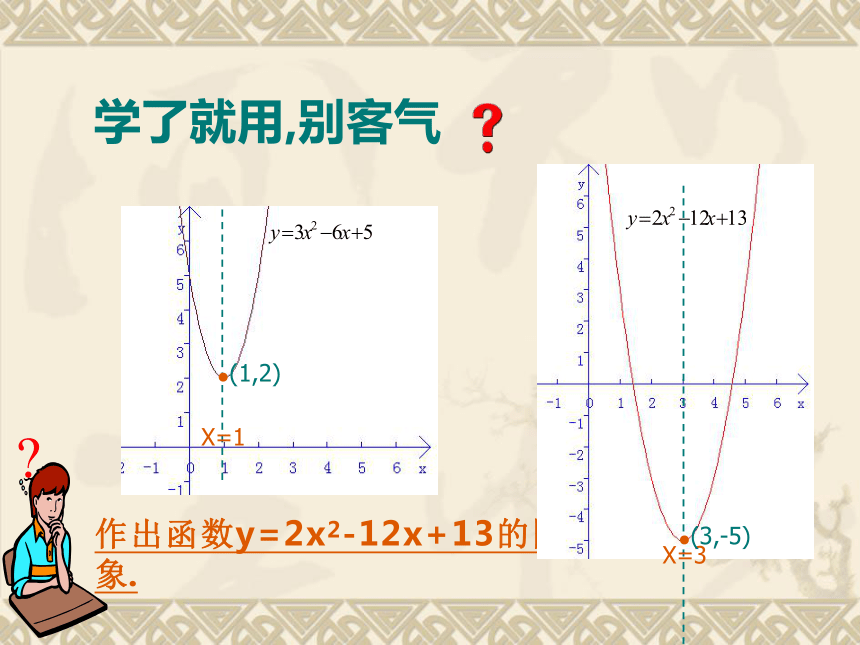
配方后的表达式通常称为顶点式直接画函数y=ax2+bx+c的图象4.画对称轴,描点,连线:作出二次函数y=3(x-1)2+2的图象. 2.根据配方式(顶点式)确定开口方向,对称轴,顶点坐标.3.列表:根据对称性,选取适当值列表计算.∵a=3>0,∴开口向上;对称轴:直线x=1;顶点坐标:(1,2).学了就用,别客气作出函数y=2x2-12x+13的图象. ●(1,2)●(3,-5)例.求次函数y=ax2+bx+c的对称轴和顶点坐标. 函数y=ax2+bx+c的顶点式 一般地,对于二次函数y=ax2+bx+c,我们可以利用配方法推导出它的对称轴和顶点坐标. 1.配方:提取二次项系数配方:加上再减去一次项系数绝对值一半的平方整理:前三项化为平方形式,后两项合并同类项化简:去掉中括号老师提示:
结果通常称为顶点坐标公式.顶点坐标公式因此,二次函数y=ax2+bx+c的图象是一条抛物线.根据公式确定下列二次函数图象的对称轴和顶点坐标: 请你总结函数
函数y=ax2+bx+c(a≠0)
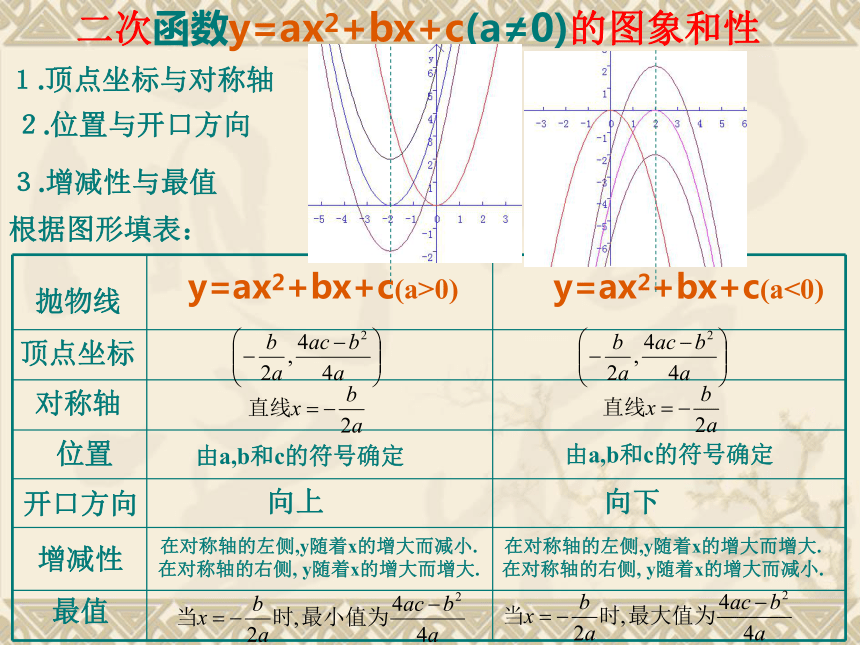
的图象和性质 想一想,函数y=ax2+bx+c和y=ax2的图象之间的关系是什么?二次函数y=ax2+bx+c(a≠0)的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定向上向下在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:1.相同点: (1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 . 2.不同点: (1)位置不同(2)顶点不同:分别是 和(0,0).
(3)对称轴不同:分别是 和y轴.
(4)最值不同:分别是 和0.
3.联系: y=a(x-h)2+k(a≠0) 的图象可以看成y=ax2的图象先沿x轴整体左(右)平移| |个单位(当 >0时,向右平移;当 <0时,向左平移),再沿对称轴整体上(下)平移| |个单位 (当 >0时向上平移;当 <0时,向下平移)得到的.回味无穷二次函数y=ax2+bx+c(a≠0)与y=ax2的关系1.确定下列二次函数的开口方向、对称轴和顶点坐标. 2. (2011山东威海)二次函数 的图象如图所示.当y<0时,自变量x的取值范围是( ).
A.-1<x<3 B.x<-1
C. x>3 D.x<-1或x>3【答案】A3、二次函数 的图像向左平移2个单位,再向上平移3个单位,得到函数解析式 则b与c分别等于( )
(A)2,-2 (B)-8,14
(C)-6,6 (D)-8,184
4、抛物线 的顶点在x轴上方的条件是( )
(A) (B)
(C) (D)5. (2011山东菏泽) 如图为抛物线
的图像,A、B、C 为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是
A.a+b=-1 B. a-b=-1 C. b<2a D. ac<0
【答案】B6.(2011四川重庆,7,4分)已知抛物线 y=ax2+bx+c(a≠0)在平面直角坐标系中的 位置如图所示,则下列结论中正确的是( ) A. a>0 B. b<0 C. c<0 D. a+b+c>0 【答案】D7. (2011台湾台北)若下列有一图形为二次函数y=2x2-8x+6的图形,则此图为何?
【答案】A8. (2011台湾全区)图为坐标平面上二次函数
的图象,且此图象通(-1 , 1)、(2 ,-1)两点.下列关于此二次函数的叙述,何者正确?
A .y的最大值小于0 B.当x=0时,y的值大于1
C.当x=1时,y的值大于1
D.当x=3时,y的值小于0【答案】D 9. (2011甘肃兰州,9,4分)如图所示的二次函数
的图象中,刘星同学观察得出了下面四条信息:(1) ;(2)c>1;
(3)2a-b<0;(4)a+b+c<0。
你认为其中错误的有( )
A.2个 B.3个
C.4个 D.1个【答案】D10. (2011广东肇庆)二次函数 有 A. 最大值 B. 最小值 C. 最大值 D. 最小值【答案】D11. (2011四川凉山州)二次函数 的图像如图所示,反比列函数 与正比列函数 在同一坐标系内的大致图像是( ) 【答案】B12、在直角坐标系中,抛物线 的顶点A在x轴负半轴上,抛物线上一点C的横坐标为1,且AC= ,求此抛物线的函数解析式。快乐学习每一天结束寄语探索是数学的生命线.再见如图,两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关手y轴对称. ⑴钢缆的最低点到桥面的距离是少?
⑵两条钢缆最低点之间的距离是多少?
⑶你是怎样计算的?与同伴交流.函数y=ax2+bx+c(a≠0)的应用⑴.钢缆的最低点到桥面的距离是少?你是怎样计算的?与同伴交流.可以将函数y=0.0225x2+0.9x+10配方,求得顶点坐标,从而获得钢缆的最低点到桥面的距离;由此可知钢缆的最低点到桥面的距离是1m。⑵两条钢缆最低点之间的距离是多少?你是怎样计算的? 与同伴交流.想一想,你知道图中右面钢缆的表达式是什么吗? ⑶你还有其它方法吗?与同伴交流.直接利用顶点坐标公式再计算一下上面问题中钢缆的最低点到桥面的距离以及两条钢缆最低点之间的距离. 由此可知钢缆的最低点
到桥面的距离是1m。
君子耻其言而过其行5.6二次函数图象和性质(3)二次函数y=ax2+bx+c的图象和性质 二次函数y=3(x-1)2+2的图象是由
向 平移 单位,再向 平移 单
位得到的;它的开口 ,对称轴是 ,
顶点坐标是 ,复习y=3(x-1)2+2
=3x2-6x+5你能说出y=3x2-6x+5的图像的对
称轴和顶点坐标吗?y=3x2-6x+5
=3(x-1)2+2怎样直接作出函数y=3x2-6x+5的图象?函数y=ax2+bx+c的图象 我们知道,作出二次函数y=3x2的图象,通过平移抛物线y=3x2可以得到二次函数y=3x2-6x+5的图象. 1.配方:提取二次项系数配方:加上再减去一次项系数绝对值一半的平方整理:前三项化为平方形式,后两项合并同类项化简:去掉中括号老师提示:
配方后的表达式通常称为顶点式直接画函数y=ax2+bx+c的图象4.画对称轴,描点,连线:作出二次函数y=3(x-1)2+2的图象. 2.根据配方式(顶点式)确定开口方向,对称轴,顶点坐标.3.列表:根据对称性,选取适当值列表计算.∵a=3>0,∴开口向上;对称轴:直线x=1;顶点坐标:(1,2).学了就用,别客气作出函数y=2x2-12x+13的图象. ●(1,2)●(3,-5)例.求次函数y=ax2+bx+c的对称轴和顶点坐标. 函数y=ax2+bx+c的顶点式 一般地,对于二次函数y=ax2+bx+c,我们可以利用配方法推导出它的对称轴和顶点坐标. 1.配方:提取二次项系数配方:加上再减去一次项系数绝对值一半的平方整理:前三项化为平方形式,后两项合并同类项化简:去掉中括号老师提示:
结果通常称为顶点坐标公式.顶点坐标公式因此,二次函数y=ax2+bx+c的图象是一条抛物线.根据公式确定下列二次函数图象的对称轴和顶点坐标: 请你总结函数
函数y=ax2+bx+c(a≠0)
的图象和性质 想一想,函数y=ax2+bx+c和y=ax2的图象之间的关系是什么?二次函数y=ax2+bx+c(a≠0)的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定向上向下在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:1.相同点: (1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 . 2.不同点: (1)位置不同(2)顶点不同:分别是 和(0,0).
(3)对称轴不同:分别是 和y轴.
(4)最值不同:分别是 和0.
3.联系: y=a(x-h)2+k(a≠0) 的图象可以看成y=ax2的图象先沿x轴整体左(右)平移| |个单位(当 >0时,向右平移;当 <0时,向左平移),再沿对称轴整体上(下)平移| |个单位 (当 >0时向上平移;当 <0时,向下平移)得到的.回味无穷二次函数y=ax2+bx+c(a≠0)与y=ax2的关系1.确定下列二次函数的开口方向、对称轴和顶点坐标. 2. (2011山东威海)二次函数 的图象如图所示.当y<0时,自变量x的取值范围是( ).
A.-1<x<3 B.x<-1
C. x>3 D.x<-1或x>3【答案】A3、二次函数 的图像向左平移2个单位,再向上平移3个单位,得到函数解析式 则b与c分别等于( )
(A)2,-2 (B)-8,14
(C)-6,6 (D)-8,184
4、抛物线 的顶点在x轴上方的条件是( )
(A) (B)
(C) (D)5. (2011山东菏泽) 如图为抛物线
的图像,A、B、C 为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是
A.a+b=-1 B. a-b=-1 C. b<2a D. ac<0
【答案】B6.(2011四川重庆,7,4分)已知抛物线 y=ax2+bx+c(a≠0)在平面直角坐标系中的 位置如图所示,则下列结论中正确的是( ) A. a>0 B. b<0 C. c<0 D. a+b+c>0 【答案】D7. (2011台湾台北)若下列有一图形为二次函数y=2x2-8x+6的图形,则此图为何?
【答案】A8. (2011台湾全区)图为坐标平面上二次函数
的图象,且此图象通(-1 , 1)、(2 ,-1)两点.下列关于此二次函数的叙述,何者正确?
A .y的最大值小于0 B.当x=0时,y的值大于1
C.当x=1时,y的值大于1
D.当x=3时,y的值小于0【答案】D 9. (2011甘肃兰州,9,4分)如图所示的二次函数
的图象中,刘星同学观察得出了下面四条信息:(1) ;(2)c>1;
(3)2a-b<0;(4)a+b+c<0。
你认为其中错误的有( )
A.2个 B.3个
C.4个 D.1个【答案】D10. (2011广东肇庆)二次函数 有 A. 最大值 B. 最小值 C. 最大值 D. 最小值【答案】D11. (2011四川凉山州)二次函数 的图像如图所示,反比列函数 与正比列函数 在同一坐标系内的大致图像是( ) 【答案】B12、在直角坐标系中,抛物线 的顶点A在x轴负半轴上,抛物线上一点C的横坐标为1,且AC= ,求此抛物线的函数解析式。快乐学习每一天结束寄语探索是数学的生命线.再见如图,两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关手y轴对称. ⑴钢缆的最低点到桥面的距离是少?
⑵两条钢缆最低点之间的距离是多少?
⑶你是怎样计算的?与同伴交流.函数y=ax2+bx+c(a≠0)的应用⑴.钢缆的最低点到桥面的距离是少?你是怎样计算的?与同伴交流.可以将函数y=0.0225x2+0.9x+10配方,求得顶点坐标,从而获得钢缆的最低点到桥面的距离;由此可知钢缆的最低点到桥面的距离是1m。⑵两条钢缆最低点之间的距离是多少?你是怎样计算的? 与同伴交流.想一想,你知道图中右面钢缆的表达式是什么吗? ⑶你还有其它方法吗?与同伴交流.直接利用顶点坐标公式再计算一下上面问题中钢缆的最低点到桥面的距离以及两条钢缆最低点之间的距离. 由此可知钢缆的最低点
到桥面的距离是1m。
