广东省惠州市惠阳区新圩中学2021-2022学年八年级数学下学期开学考试测试卷(含解析)
文档属性
| 名称 | 广东省惠州市惠阳区新圩中学2021-2022学年八年级数学下学期开学考试测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 275.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-06 15:10:30 | ||
图片预览



文档简介
广东省惠州市惠阳区新圩中学2021-2022学年八年级数学下册开学考试测试卷(附答案)
一、单选题:共30分。
1.下列图形既是轴对称图形,又是中心对称图形的是( )
A.平行四边形 B.三角形 C.等腰三角形 D.矩形
2.平面直角坐标系内的点A(﹣3,﹣2)与点B(3,﹣2)关于( )
A.y轴对称 B.x轴对称 C.原点对称 D.无法确定
3.在△ABC中,如果∠A﹣∠B=90°,那么△ABC是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.斜三角形
4.分式与的最简公分母是( )
A.x4﹣y4 B.(x+y)2(x2﹣y2)
C.(x﹣y)4 D.(x+y)2(x﹣y)
5.下列各组线段中,不能构成直角三角形的一组是( )
A.,1, B.1,,2 C.6,8,10 D.4,4,5
6.下列图标是轴对称图形的是( )
A. B. C. D.
7.如果一个多边形的内角和等于一个三角形的外角和的两倍,那么这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
8.下列各式从左到右变形正确的是( )
A. B. C. D.
9.如图,已知直角三角形ABC中,∠ACB=90°,∠CAB=60°,在直线BC或AC上取一点P,使得△ABP为等腰三角形,则符合条件的点有( )
A.4个 B.5个 C.6个 D.7个
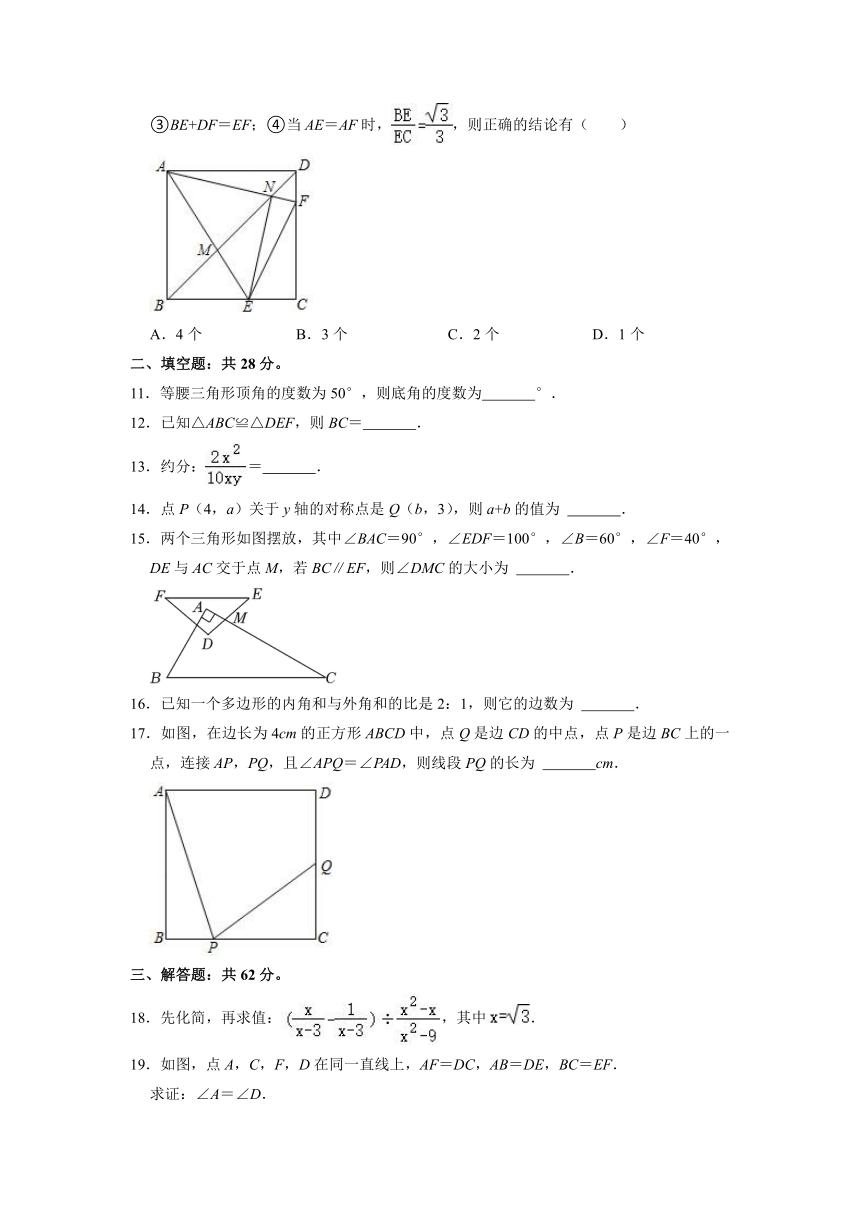
10.如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N,连接EN、EF.有以下结论:①△AMN∽△BME;②AN=EN;③BE+DF=EF;④当AE=AF时,,则正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题:共28分。
11.等腰三角形顶角的度数为50°,则底角的度数为 °.
12.已知△ABC≌△DEF,则BC= .
13.约分:= .
14.点P(4,a)关于y轴的对称点是Q(b,3),则a+b的值为 .
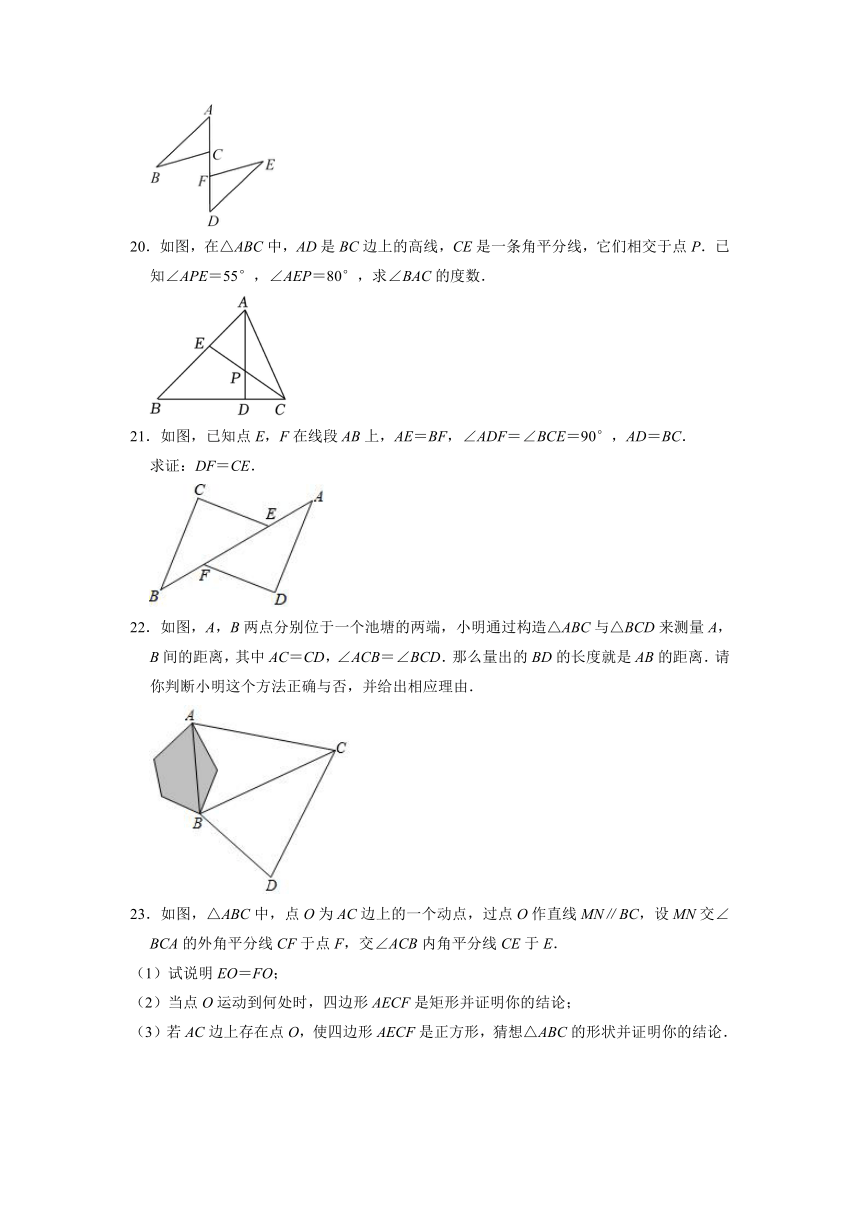
15.两个三角形如图摆放,其中∠BAC=90°,∠EDF=100°,∠B=60°,∠F=40°,DE与AC交于点M,若BC∥EF,则∠DMC的大小为 .
16.已知一个多边形的内角和与外角和的比是2:1,则它的边数为 .
17.如图,在边长为4cm的正方形ABCD中,点Q是边CD的中点,点P是边BC上的一点,连接AP,PQ,且∠APQ=∠PAD,则线段PQ的长为 cm.
三、解答题:共62分。
18.先化简,再求值:,其中.
19.如图,点A,C,F,D在同一直线上,AF=DC,AB=DE,BC=EF.
求证:∠A=∠D.
20.如图,在△ABC中,AD是BC边上的高线,CE是一条角平分线,它们相交于点P.已知∠APE=55°,∠AEP=80°,求∠BAC的度数.
21.如图,已知点E,F在线段AB上,AE=BF,∠ADF=∠BCE=90°,AD=BC.
求证:DF=CE.
22.如图,A,B两点分别位于一个池塘的两端,小明通过构造△ABC与△BCD来测量A,B间的距离,其中AC=CD,∠ACB=∠BCD.那么量出的BD的长度就是AB的距离.请你判断小明这个方法正确与否,并给出相应理由.
23.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(1)试说明EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.
24.如图,在△ABC中,BC=7cm,AC=24cm,AB=25cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,请解答下面的问题,并写出探索主要过程:
(1)经过多少时间后,P、Q两点的距离为5cm?
(2)经过多少时间后,S△PCQ的面积为15cm2?
(3)用含t的代数式表示△PCQ的面积,并用配方法说明t为何值时△PCQ的面积最大,最大面积是多少?
25.已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图③.写出AF、EF与AB的数量关系,并对图②进行证明.
参考答案
一、单选题:共30分。
1.解:A.平行四边形不是轴对称图形,是中心对称图形,故本选项不符合题意;
B.三角形不一定是轴对称图形,不是中心对称图形,故本选项不符合题意;
C.等腰三角形是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
2.解:平面直角坐标系内的点A(﹣3,﹣2)与点B(3,﹣2)关于y轴对称.
故选:A.
3.解:在△ABC中,∵∠A﹣∠B=90°,
∴∠A=90°+∠B>90°(∠B肯定大于0),那么△ABC是钝角三角形.
故选:B.
4.解:∵x2﹣y2=(x+y)(x﹣y),
∴(x+y)2与x2﹣y2的最简公分母为(x+y)2(x﹣y),
故选:D.
5.解:A.∵()2+12=+1=,()2=,
∴()2+12=()2,
∴以,1,为边能组成直角三角形,故本选项不符合题意;
B.∵12+22=1+4=5,()2=5,
∴12+22=()2,
∴以1,2,为边能组成直角三角形,故本选项不符合题意;
C.∵62+82=36+64=100,102=100,
∴62+82=102,
∴以6,8,10为边能组成直角三角形,故本选项不符合题意;
D.∵42+42=16+16=32,52=25,
∴42+42≠52,
∴以4,4,5为边不能组成直角三角形,故本选项符合题意;
故选:D.
6.解:A,B,D选项中的图形都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
C选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:C.
7.解:根据题意得,
(n﹣2) 180=360×2,
解得n=6,
故选:D.
8.解:A. =,所以A选项不符合题意;
B. =(m≠0),所以B选项不符合题意;
C. =,所以C选项不符合题意;
D. =,所以D选项符合题意.
故选:D.
9.解:①AB的垂直平分线交直线AC于点P1,交BC于点P2,(此时PA=PB);
②以A为圆心,AB为半径画圆,交AC于二点P3,P1,交BC于点P4,(此时AB=AP);
③以B为圆心,BA为半径画圆,交BC有二点P5,P6,交AC有一点P1(此时BP=BA).
故符合条件的点有6个.
故选:C.
10.解:①∵四边形ABCD是正方形,∠EAF=45°,
∴∠CBD=∠EAF=45°,
又∵∠BME=∠AMN,
∴△AMN∽△BME,
故①正确;
②由①知△AMN∽△BME,
∴,
∴,
∵∠AMB=∠EMN,
∴△AMB∽△NME,
∴∠NEA=∠ABM,
∵∠ABM=∠CBD=45°,∠EAF=45°,
∴∠NEA=∠EAF=45°,
∴AN=EN,
故②正确;
③如图,将△ADF绕点A顺时针旋转90°得到△ABH,
则AF=AH,∠DAF=∠BAH,
∵∠EAF=45°=∠DAF+∠BAE=∠HAE,
∵∠ABE=∠ABH=90°,
∴H,B,E共线,
在△AEF与△AEH中,
,
∴△AEF≌△AEH(SAS),
∴EF=EH=BE+BH=BE+DF,
故③正确;
④在△ABE与△ADF中,
,
∴△ABE≌△ADF(SAS),
∴BE=DF,∠BAE=∠DAF=22.5°,
∵BC=CD,
∴CE=CF,
假设正方形边长为1,设CE=x,则BE=1﹣x,
如图,连接AC,交EF于O
,
∵AE=AF,CE=CF,
∴AC是EF的垂直平分线,
∴AC⊥EF,OE=OF,
∵∠BAC=45°,
∴∠EAC=22.5°,
∴BE=EO=1﹣x,
∴(1﹣x)=x,
∴x=2﹣,
∴,
故④错误,
故选:B.
二、填空题:共28分。
11.解:∵三角形为等腰三角形,且顶角为50°,
∴底角=(180°﹣50°)÷2=65°.
故答案为:65.
12.解:∵△ABC≌△DEF,
∴BC=EF,
故答案为:EF.
13.解:原式==.
故答案为:.
14.解:∵点P(4,a)关于y轴的对称点Q(b,3),
∴a=3,b=﹣4,
∴a+b=3+(﹣4)=﹣1.
故答案为:﹣1.
15.解:延长ED交CB的延长线于点G,
∵∠BAC=90°,∠ABC=60°,
∴∠C=90°﹣∠ABC=30°,
∵∠EDF=100°,∠F=40°,
∴∠E=180°﹣∠F﹣∠EDF=40°,
∵EF∥BC,
∴∠E=∠G=40°,
∴∠DMC=180°﹣∠C﹣∠G=110°,
故答案为:110°.
16.解:内角和是2×360=720°.
设多边形的边数是n,根据题意得:
(n﹣2) 180=720.
解得n=6.
故答案为:6.
17.解:如图,延长AD,PQ交于点H,
设PC=xcm,
∵四边形ABCD是正方形,
∴AD=CD=BC=4cm,AD∥BC,
∵点Q是边CD的中点,
∴DQ=CQ=2cm,
∵AD∥BC,
∴∠H=∠QPC,
又∵∠DQH=∠CQP,
∴△DQH≌△CQP(AAS),
∴PC=DH=xcm,PQ=QH,
∴AH=AD+DH=(4+x)cm,
∵∠APQ=∠PAD,
∴AH=PH=(4+x)cm,
∴PQ=QH=()cm,
∵PQ2=CQ2+PC2,
∴()2=4+x2,
∴x=或x=0(舍),
∴PQ=cm,
故答案为:.
三、解答题:共62分。
18.解:原式=
=
=,
当时,
原式=.
19.证明:∵AF=DC,
∴AF﹣CF=DC﹣CF,
∴AC=DF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠A=∠D.
20.解:∵AD⊥BC,
∴∠PDC=90°,
∵∠CPD=∠APE=55°,
∴∠PCD=90°﹣55°=35°,
∵CE是一条角平分线,
∴∠ACE=∠PCD=35°,
∴∠BAC=180°﹣35°﹣80°=65°.
21.证明:∵AE=BF,
∴AF=BE,且∠ADF=∠BCE=90°,AD=BC,
∴Rt△ADF≌Rt△BCE(HL),
∴DF=CE.
22.解:正确;理由如下:
在△ABC与△DBC中,
.
∴△ABC≌△DBC(SAS).
∴AB=DB.
23.解:(1)∵CE平分∠ACB,
∴∠ACE=∠BCE,
∵MN∥BC,
∴∠OEC=∠ECB,
∴∠OEC=∠OCE,
∴OE=OC,
同理OC=OF,
∴OE=OF.
(2)当点O运动到AC中点处时,四边形AECF是矩形.
如图AO=CO,EO=FO,
∴四边形AECF为平行四边形,
∵CE平分∠ACB,
∴∠ACE=∠ACB,
同理,∠ACF=∠ACG,
∴∠ECF=∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°,
∴四边形AECF是矩形.
(3)当△ABC是直角三角形且∠ACB=90°时,在AC边上存在点O(为其中点),使四边形AECF是正方形.
证明:∵∠ACB=90°,
∴AC⊥BC.
∵MN∥BC,
∴AC⊥MN,即AC⊥EF.
由(2)知,四边形AECF是矩形,
∴矩形AECF是正方形.
24.解:(1)连接PQ,
设经过ts后,P、Q两点的距离为5cm,
ts后,PC=7﹣2tcm,CQ=5tcm,
根据勾股定理可知PC2+CQ2=PQ2,
代入数据(7﹣2t)2+(5t)2=(5)2;
解得t=1或t=﹣(不合题意舍去);
(2)设经过ts后,S△PCQ的面积为15cm2
ts后,PC=7﹣2tcm,CQ=5tcm,
S△PCQ=×PC×CQ=×(7﹣2t)×5t=15
解得t1=2,t2=1.5,
经过2或1.5s后,S△PCQ的面积为15cm2.
(3)设经过ts后,△PCQ的面积最大,
ts后,PC=7﹣2tcm,CQ=5tcm,
S△PCQ=×PC×CQ=×(7﹣2t)×5t=×(﹣2t2+7t).
=﹣5.
∴当t=s时,△PCQ的面积最大,最大值为cm2.
25.(1)证明:如图①,延长AD、EF交于点G,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠G=∠BAD,
∴∠G=∠CAD,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(AAS),
∴AB=GE,
∵GE=FG+EF=AF+EF,
∴AF+EF=AB;
(2)结论:AF﹣EF=AB.
证明:如图②,延长AD、EF交于点G,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠G=∠BAD,
∴∠G=∠CAD,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(AAS),
∴AB=GE,
∵GE=FG﹣EF=AF﹣EF,
∴AF﹣EF=AB;
(3)结论:EF﹣AF=AB.
证明:如图③,延长AD交EF于点G,
∵AD平分∠PAC,
∴∠PAD=∠CAD,
∵EF∥AB,
∴∠AGF=∠PAD,
∴∠AGF=∠CAD,∠ABD=∠GED,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(ASA),
∴AB=GE,
∵EF﹣FG=GE,
∴EF﹣AF=AB;
一、单选题:共30分。
1.下列图形既是轴对称图形,又是中心对称图形的是( )
A.平行四边形 B.三角形 C.等腰三角形 D.矩形
2.平面直角坐标系内的点A(﹣3,﹣2)与点B(3,﹣2)关于( )
A.y轴对称 B.x轴对称 C.原点对称 D.无法确定
3.在△ABC中,如果∠A﹣∠B=90°,那么△ABC是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.斜三角形
4.分式与的最简公分母是( )
A.x4﹣y4 B.(x+y)2(x2﹣y2)
C.(x﹣y)4 D.(x+y)2(x﹣y)
5.下列各组线段中,不能构成直角三角形的一组是( )
A.,1, B.1,,2 C.6,8,10 D.4,4,5
6.下列图标是轴对称图形的是( )
A. B. C. D.
7.如果一个多边形的内角和等于一个三角形的外角和的两倍,那么这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
8.下列各式从左到右变形正确的是( )
A. B. C. D.
9.如图,已知直角三角形ABC中,∠ACB=90°,∠CAB=60°,在直线BC或AC上取一点P,使得△ABP为等腰三角形,则符合条件的点有( )
A.4个 B.5个 C.6个 D.7个
10.如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N,连接EN、EF.有以下结论:①△AMN∽△BME;②AN=EN;③BE+DF=EF;④当AE=AF时,,则正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题:共28分。
11.等腰三角形顶角的度数为50°,则底角的度数为 °.
12.已知△ABC≌△DEF,则BC= .
13.约分:= .
14.点P(4,a)关于y轴的对称点是Q(b,3),则a+b的值为 .
15.两个三角形如图摆放,其中∠BAC=90°,∠EDF=100°,∠B=60°,∠F=40°,DE与AC交于点M,若BC∥EF,则∠DMC的大小为 .
16.已知一个多边形的内角和与外角和的比是2:1,则它的边数为 .
17.如图,在边长为4cm的正方形ABCD中,点Q是边CD的中点,点P是边BC上的一点,连接AP,PQ,且∠APQ=∠PAD,则线段PQ的长为 cm.
三、解答题:共62分。
18.先化简,再求值:,其中.
19.如图,点A,C,F,D在同一直线上,AF=DC,AB=DE,BC=EF.
求证:∠A=∠D.
20.如图,在△ABC中,AD是BC边上的高线,CE是一条角平分线,它们相交于点P.已知∠APE=55°,∠AEP=80°,求∠BAC的度数.
21.如图,已知点E,F在线段AB上,AE=BF,∠ADF=∠BCE=90°,AD=BC.
求证:DF=CE.
22.如图,A,B两点分别位于一个池塘的两端,小明通过构造△ABC与△BCD来测量A,B间的距离,其中AC=CD,∠ACB=∠BCD.那么量出的BD的长度就是AB的距离.请你判断小明这个方法正确与否,并给出相应理由.
23.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(1)试说明EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.
24.如图,在△ABC中,BC=7cm,AC=24cm,AB=25cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,请解答下面的问题,并写出探索主要过程:
(1)经过多少时间后,P、Q两点的距离为5cm?
(2)经过多少时间后,S△PCQ的面积为15cm2?
(3)用含t的代数式表示△PCQ的面积,并用配方法说明t为何值时△PCQ的面积最大,最大面积是多少?
25.已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图③.写出AF、EF与AB的数量关系,并对图②进行证明.
参考答案
一、单选题:共30分。
1.解:A.平行四边形不是轴对称图形,是中心对称图形,故本选项不符合题意;
B.三角形不一定是轴对称图形,不是中心对称图形,故本选项不符合题意;
C.等腰三角形是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
2.解:平面直角坐标系内的点A(﹣3,﹣2)与点B(3,﹣2)关于y轴对称.
故选:A.
3.解:在△ABC中,∵∠A﹣∠B=90°,
∴∠A=90°+∠B>90°(∠B肯定大于0),那么△ABC是钝角三角形.
故选:B.
4.解:∵x2﹣y2=(x+y)(x﹣y),
∴(x+y)2与x2﹣y2的最简公分母为(x+y)2(x﹣y),
故选:D.
5.解:A.∵()2+12=+1=,()2=,
∴()2+12=()2,
∴以,1,为边能组成直角三角形,故本选项不符合题意;
B.∵12+22=1+4=5,()2=5,
∴12+22=()2,
∴以1,2,为边能组成直角三角形,故本选项不符合题意;
C.∵62+82=36+64=100,102=100,
∴62+82=102,
∴以6,8,10为边能组成直角三角形,故本选项不符合题意;
D.∵42+42=16+16=32,52=25,
∴42+42≠52,
∴以4,4,5为边不能组成直角三角形,故本选项符合题意;
故选:D.
6.解:A,B,D选项中的图形都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
C选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:C.
7.解:根据题意得,
(n﹣2) 180=360×2,
解得n=6,
故选:D.
8.解:A. =,所以A选项不符合题意;
B. =(m≠0),所以B选项不符合题意;
C. =,所以C选项不符合题意;
D. =,所以D选项符合题意.
故选:D.
9.解:①AB的垂直平分线交直线AC于点P1,交BC于点P2,(此时PA=PB);
②以A为圆心,AB为半径画圆,交AC于二点P3,P1,交BC于点P4,(此时AB=AP);
③以B为圆心,BA为半径画圆,交BC有二点P5,P6,交AC有一点P1(此时BP=BA).
故符合条件的点有6个.
故选:C.
10.解:①∵四边形ABCD是正方形,∠EAF=45°,
∴∠CBD=∠EAF=45°,
又∵∠BME=∠AMN,
∴△AMN∽△BME,
故①正确;
②由①知△AMN∽△BME,
∴,
∴,
∵∠AMB=∠EMN,
∴△AMB∽△NME,
∴∠NEA=∠ABM,
∵∠ABM=∠CBD=45°,∠EAF=45°,
∴∠NEA=∠EAF=45°,
∴AN=EN,
故②正确;
③如图,将△ADF绕点A顺时针旋转90°得到△ABH,
则AF=AH,∠DAF=∠BAH,
∵∠EAF=45°=∠DAF+∠BAE=∠HAE,
∵∠ABE=∠ABH=90°,
∴H,B,E共线,
在△AEF与△AEH中,
,
∴△AEF≌△AEH(SAS),
∴EF=EH=BE+BH=BE+DF,
故③正确;
④在△ABE与△ADF中,
,
∴△ABE≌△ADF(SAS),
∴BE=DF,∠BAE=∠DAF=22.5°,
∵BC=CD,
∴CE=CF,
假设正方形边长为1,设CE=x,则BE=1﹣x,
如图,连接AC,交EF于O
,
∵AE=AF,CE=CF,
∴AC是EF的垂直平分线,
∴AC⊥EF,OE=OF,
∵∠BAC=45°,
∴∠EAC=22.5°,
∴BE=EO=1﹣x,
∴(1﹣x)=x,
∴x=2﹣,
∴,
故④错误,
故选:B.
二、填空题:共28分。
11.解:∵三角形为等腰三角形,且顶角为50°,
∴底角=(180°﹣50°)÷2=65°.
故答案为:65.
12.解:∵△ABC≌△DEF,
∴BC=EF,
故答案为:EF.
13.解:原式==.
故答案为:.
14.解:∵点P(4,a)关于y轴的对称点Q(b,3),
∴a=3,b=﹣4,
∴a+b=3+(﹣4)=﹣1.
故答案为:﹣1.
15.解:延长ED交CB的延长线于点G,
∵∠BAC=90°,∠ABC=60°,
∴∠C=90°﹣∠ABC=30°,
∵∠EDF=100°,∠F=40°,
∴∠E=180°﹣∠F﹣∠EDF=40°,
∵EF∥BC,
∴∠E=∠G=40°,
∴∠DMC=180°﹣∠C﹣∠G=110°,
故答案为:110°.
16.解:内角和是2×360=720°.
设多边形的边数是n,根据题意得:
(n﹣2) 180=720.
解得n=6.
故答案为:6.
17.解:如图,延长AD,PQ交于点H,
设PC=xcm,
∵四边形ABCD是正方形,
∴AD=CD=BC=4cm,AD∥BC,
∵点Q是边CD的中点,
∴DQ=CQ=2cm,
∵AD∥BC,
∴∠H=∠QPC,
又∵∠DQH=∠CQP,
∴△DQH≌△CQP(AAS),
∴PC=DH=xcm,PQ=QH,
∴AH=AD+DH=(4+x)cm,
∵∠APQ=∠PAD,
∴AH=PH=(4+x)cm,
∴PQ=QH=()cm,
∵PQ2=CQ2+PC2,
∴()2=4+x2,
∴x=或x=0(舍),
∴PQ=cm,
故答案为:.
三、解答题:共62分。
18.解:原式=
=
=,
当时,
原式=.
19.证明:∵AF=DC,
∴AF﹣CF=DC﹣CF,
∴AC=DF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠A=∠D.
20.解:∵AD⊥BC,
∴∠PDC=90°,
∵∠CPD=∠APE=55°,
∴∠PCD=90°﹣55°=35°,
∵CE是一条角平分线,
∴∠ACE=∠PCD=35°,
∴∠BAC=180°﹣35°﹣80°=65°.
21.证明:∵AE=BF,
∴AF=BE,且∠ADF=∠BCE=90°,AD=BC,
∴Rt△ADF≌Rt△BCE(HL),
∴DF=CE.
22.解:正确;理由如下:
在△ABC与△DBC中,
.
∴△ABC≌△DBC(SAS).
∴AB=DB.
23.解:(1)∵CE平分∠ACB,
∴∠ACE=∠BCE,
∵MN∥BC,
∴∠OEC=∠ECB,
∴∠OEC=∠OCE,
∴OE=OC,
同理OC=OF,
∴OE=OF.
(2)当点O运动到AC中点处时,四边形AECF是矩形.
如图AO=CO,EO=FO,
∴四边形AECF为平行四边形,
∵CE平分∠ACB,
∴∠ACE=∠ACB,
同理,∠ACF=∠ACG,
∴∠ECF=∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°,
∴四边形AECF是矩形.
(3)当△ABC是直角三角形且∠ACB=90°时,在AC边上存在点O(为其中点),使四边形AECF是正方形.
证明:∵∠ACB=90°,
∴AC⊥BC.
∵MN∥BC,
∴AC⊥MN,即AC⊥EF.
由(2)知,四边形AECF是矩形,
∴矩形AECF是正方形.
24.解:(1)连接PQ,
设经过ts后,P、Q两点的距离为5cm,
ts后,PC=7﹣2tcm,CQ=5tcm,
根据勾股定理可知PC2+CQ2=PQ2,
代入数据(7﹣2t)2+(5t)2=(5)2;
解得t=1或t=﹣(不合题意舍去);
(2)设经过ts后,S△PCQ的面积为15cm2
ts后,PC=7﹣2tcm,CQ=5tcm,
S△PCQ=×PC×CQ=×(7﹣2t)×5t=15
解得t1=2,t2=1.5,
经过2或1.5s后,S△PCQ的面积为15cm2.
(3)设经过ts后,△PCQ的面积最大,
ts后,PC=7﹣2tcm,CQ=5tcm,
S△PCQ=×PC×CQ=×(7﹣2t)×5t=×(﹣2t2+7t).
=﹣5.
∴当t=s时,△PCQ的面积最大,最大值为cm2.
25.(1)证明:如图①,延长AD、EF交于点G,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠G=∠BAD,
∴∠G=∠CAD,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(AAS),
∴AB=GE,
∵GE=FG+EF=AF+EF,
∴AF+EF=AB;
(2)结论:AF﹣EF=AB.
证明:如图②,延长AD、EF交于点G,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠G=∠BAD,
∴∠G=∠CAD,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(AAS),
∴AB=GE,
∵GE=FG﹣EF=AF﹣EF,
∴AF﹣EF=AB;
(3)结论:EF﹣AF=AB.
证明:如图③,延长AD交EF于点G,
∵AD平分∠PAC,
∴∠PAD=∠CAD,
∵EF∥AB,
∴∠AGF=∠PAD,
∴∠AGF=∠CAD,∠ABD=∠GED,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(ASA),
∴AB=GE,
∵EF﹣FG=GE,
∴EF﹣AF=AB;
同课章节目录
