青岛版八下7.8《实数(1)》课件

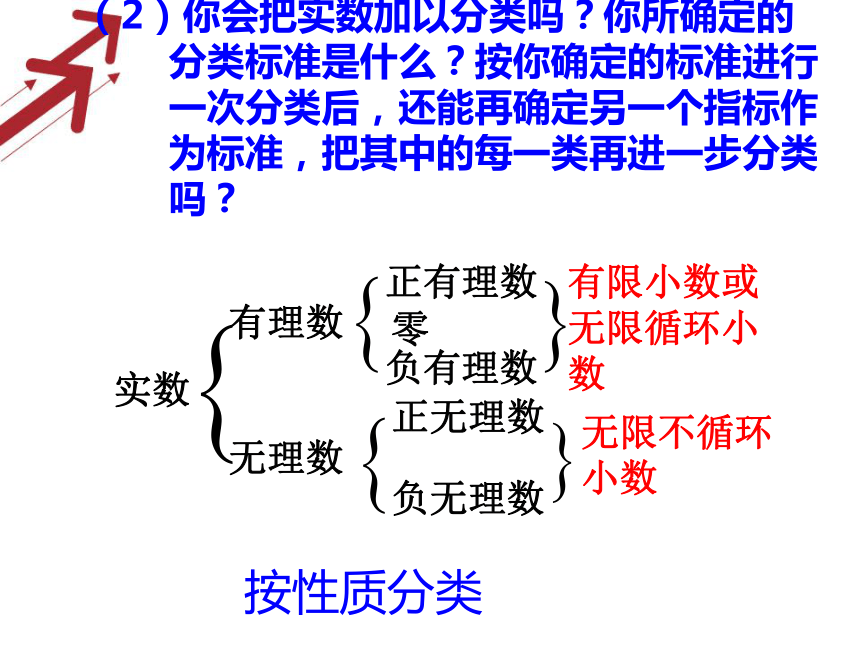
课件23张PPT。7.8 实数（1）知识回顾1、无理数：无限不循环小数叫做无理数2、有理数：有限和无限循环小数属于有理数或整数与分数统称为有理数（1）到目前为止，你认识了哪些数？ 自然数 分数负数 有理数 小数负整数 正整数 零 有限小数 无限不循环小数-无理数负有理数 想一想（2）你会把实数加以分类吗？你所确定的分类标准是什么？按你确定的标准进行一次分类后，还能再确定另一个指标作为标准，把其中的每一类再进一步分类吗？按性质分类实数按大小分类有一定的规律，但不循环的无限小数都是无理数。
0.1010010001…〔两个1之间依次多1个0〕
—234.232232223…〔两个3之间依次多1个2〕0.12345678910111213 …〔小数部分有相继的正整数组成〕
例如
像 的数是无理数。
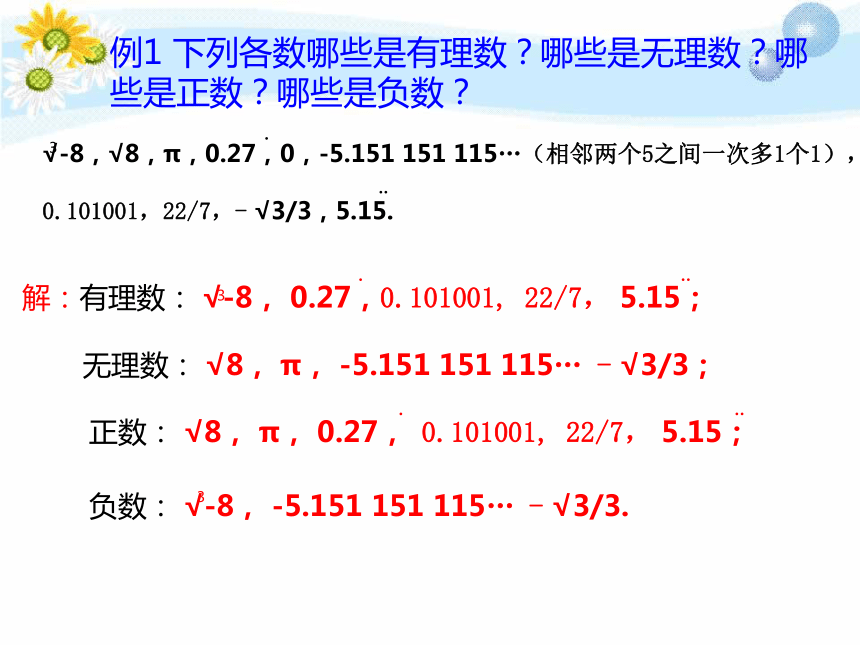
圆周率 及一些含有 的数都是无理数思考：一个无理数的相反数与绝对值分别是什么数？例1 下列各数哪些是有理数？哪些是无理数？哪些是正数？哪些是负数？√-8，√8，π，0.27，0，-5.151 151 115…（相邻两个5之间一次多1个1），
0.101001，22/7，- √3/3，5.15.3...解：有理数： √-8， 0.27，0.101001, 22/7， 5.15；3...无理数： √8， π， -5.151 151 115… - √3/3；正数： √8， π， 0.27， 0.101001, 22/7， 5.15； ...负数： √-8， -5.151 151 115… - √3/3. 3练习 将下列各数放入图中适当的位置： -0.101001000100001、　 、 4、 3.14、0.373373337……40、-2-0.101001000100001、3.14、0.373373337… (它的位数无限且相邻的两个3之间7的个数依次加1)0、-2、练习 判断下列说法是否正确：议一议1AB 如图:OA=OB,数轴上A点对应的数是什么? 如果将所有有理数都标到数轴上,那么数轴被填满了吗? 1、每个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.即实数和数轴上点是一一对应的. 2、同样,在数轴上,右边的点表示的数比左边的点表示的数大.总结：4、有序实数对与坐标平面上的点也是一一对应的。3、如果a是实数，那么｜a｜就是在数轴上表示数a的点，到原点的距离。 在实数范围内，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。在数轴上作出 的对应点.0123-112012-1-2A一个实数a-1-10-110-110-1310-1310-13313013-1013 1、每个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.即实数和数轴上点是一一对应的. 2、同样,在数轴上,右边的点表示的数比左边的点表示的数大.数轴上一个点有一个实数有一个实数数轴上一个点例如：例2 比较下列各组数中两个数的大小：（1）3.14与π； （2）-√3与√-3.3解：（1）∵π≈3.141，
∴3.14<π.（2）∵ -√3 ≈-1.732，
√-3 ≈-1.442
∴ -√3< √-3 33例3 求下列各数的相反数和绝对值：（1）2-√3； （2） √5-√6.解：（1）2-√3的相反数是-（ 2-√3 ）
=-2+√3
∵ √3<2，
∴ 2-√3>0，
∴ |2-√3|=2-√3.（2） √5-√6的相反数是-（ √5-√6 ）
=- √5+√6= √6-√5
∵ √5<√6，
∴ √5-√6<0，
∴ |√5-√6|= √6-√5.练习：求下列各数的相反数、倒数和绝对值：22-771、a、b互为相反数，c与d互为倒数则a+1+b+cd=
。2、实数a,b,c,d在数轴上的对应点如图1－1所示，则
它们从小到大的顺序是 。其中：2c