17.1 勾股定理(2)
文档属性
| 名称 | 17.1 勾股定理(2) |  | |
| 格式 | zip | ||
| 文件大小 | 783.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-12 09:30:31 | ||
图片预览




文档简介
课件12张PPT。八年级 下册17.1 勾股定理(2)本课是在学习勾股定理的基础上,学习应用勾股定
理进行直角三角形的边长计算,解决一些简单的实
际问题.课件说明课件说明学习目标:
1.能运用勾股定理求线段长度,并解决一些简单的
实际问题;
2.在利用勾股定理解决实际生活问题的过程中,能
从实际问题中抽象出直角三角形这一几何模型,
利用勾股定理建立已知边与未知边长度之间的联
系,并进一步求出未知边长.
学习重点:
运用勾股定理计算线段长度,解决实际问题. 已知一个直角三角形的两边,应用勾股定理可以求
出第三边,这在求距离时有重要作用.说一说 勾股定理:
如果直角三角形的两条直角边长分别为a,b,斜边
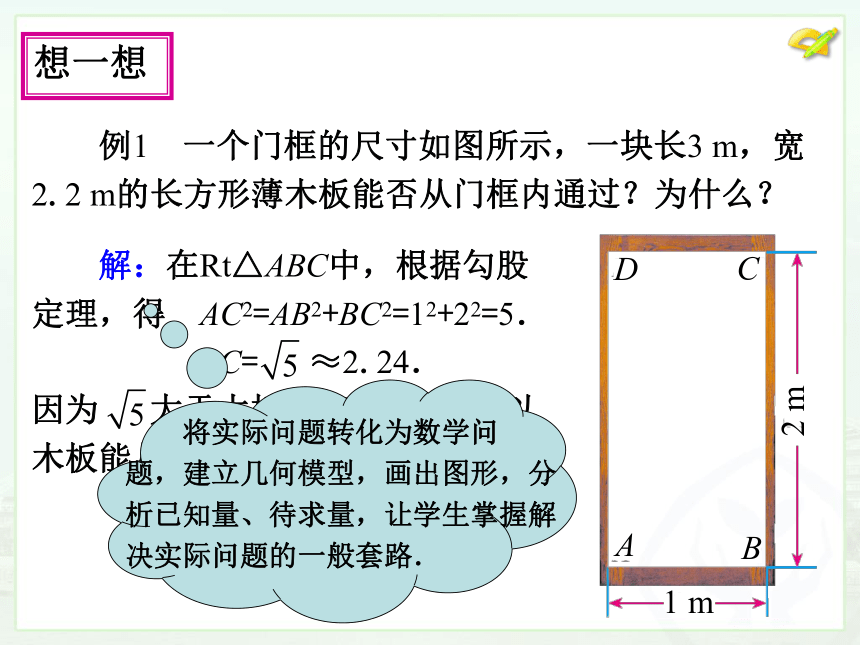
长为c,那么a2+b2=c2.想一想 例1 一个门框的尺寸如图所示,一块长3 m,宽
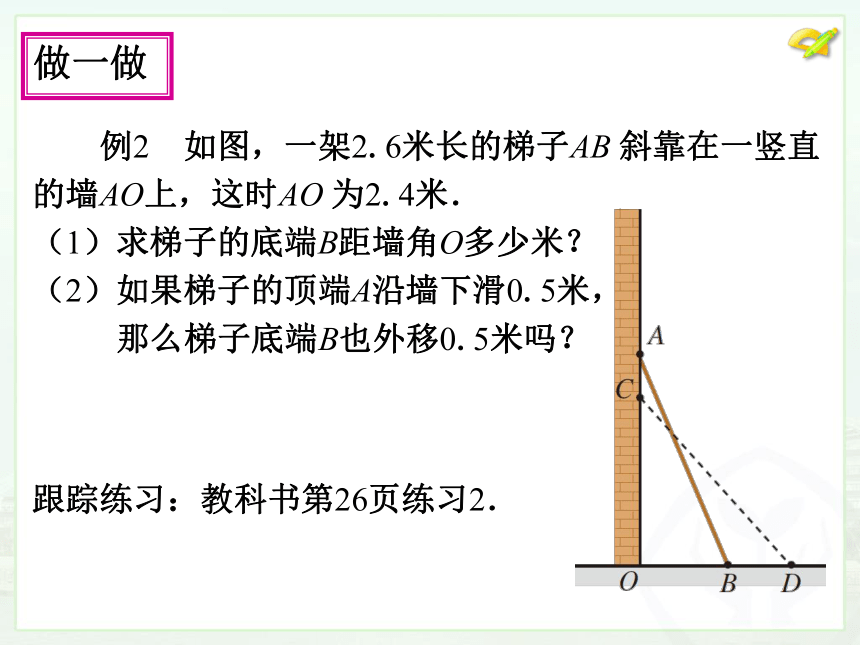
2.2 m的长方形薄木板能否从门框内通过?为什么? 跟踪练习:教科书第26页练习2. 做一做 例2 如图,一架2.6米长的梯子AB 斜靠在一竖直
的墙AO上,这时AO 为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5米,
那么梯子底端B也外移0.5米吗?想一想 问题 如果知道平面直角坐标系坐标轴上任意两点
的坐标为(x,0),(0,y),你能求这两点之间的距
离吗? 拓展提高 形成技能 今有池方一丈,葭生其中央,出水一尺,引葭赴岸,
适与岸齐.问水深、葭长各几何?拓展提高 形成技能 今有池方一丈,葭生其中央,出水一尺,引葭赴岸,
适与岸齐.问水深、葭长各几何? 利用勾股定理解决实际问题
的一般思路:
(1)重视对实际问题题意的
正确理解;
(2)建立对应的数学模型,
运用相应的数学知识;
(3)方程思想在本题中的运
用.巩固练习 如图,一棵树被台风吹折断后,树顶端落在离底端
3米处,测得折断后长的一截比短的一截长1米,你能计
算树折断前的高度吗?课堂小结 (1)利用勾股定理解决实际问题有哪些基本步骤?
(2)你觉得解决实际问题的难点在哪里?你有什么
好的突破办法?利用勾股定理解决实际问题的
注意点是什么?请与大家交流.
(3)本节课体现出哪些数学思想方法,都在什么情
况下运用?作业:教科书第26页第1,2题. 课后作业
理进行直角三角形的边长计算,解决一些简单的实
际问题.课件说明课件说明学习目标:
1.能运用勾股定理求线段长度,并解决一些简单的
实际问题;
2.在利用勾股定理解决实际生活问题的过程中,能
从实际问题中抽象出直角三角形这一几何模型,
利用勾股定理建立已知边与未知边长度之间的联
系,并进一步求出未知边长.
学习重点:
运用勾股定理计算线段长度,解决实际问题. 已知一个直角三角形的两边,应用勾股定理可以求
出第三边,这在求距离时有重要作用.说一说 勾股定理:
如果直角三角形的两条直角边长分别为a,b,斜边
长为c,那么a2+b2=c2.想一想 例1 一个门框的尺寸如图所示,一块长3 m,宽
2.2 m的长方形薄木板能否从门框内通过?为什么? 跟踪练习:教科书第26页练习2. 做一做 例2 如图,一架2.6米长的梯子AB 斜靠在一竖直
的墙AO上,这时AO 为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5米,
那么梯子底端B也外移0.5米吗?想一想 问题 如果知道平面直角坐标系坐标轴上任意两点
的坐标为(x,0),(0,y),你能求这两点之间的距
离吗? 拓展提高 形成技能 今有池方一丈,葭生其中央,出水一尺,引葭赴岸,
适与岸齐.问水深、葭长各几何?拓展提高 形成技能 今有池方一丈,葭生其中央,出水一尺,引葭赴岸,
适与岸齐.问水深、葭长各几何? 利用勾股定理解决实际问题
的一般思路:
(1)重视对实际问题题意的
正确理解;
(2)建立对应的数学模型,
运用相应的数学知识;
(3)方程思想在本题中的运
用.巩固练习 如图,一棵树被台风吹折断后,树顶端落在离底端
3米处,测得折断后长的一截比短的一截长1米,你能计
算树折断前的高度吗?课堂小结 (1)利用勾股定理解决实际问题有哪些基本步骤?
(2)你觉得解决实际问题的难点在哪里?你有什么
好的突破办法?利用勾股定理解决实际问题的
注意点是什么?请与大家交流.
(3)本节课体现出哪些数学思想方法,都在什么情
况下运用?作业:教科书第26页第1,2题. 课后作业
