17.1 勾股定理(3)
文档属性
| 名称 | 17.1 勾股定理(3) |

|
|
| 格式 | zip | ||
| 文件大小 | 633.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-12 00:00:00 | ||
图片预览





文档简介
课件14张PPT。八年级 下册17.1 勾股定理(3)本课首先运用勾股定理证明了直角三角形全等的HL
判定定理,从中进一步确认,一个直角三角形中,
只要两边的大小确定,则这个三角形就形状大小就
确定了.然后,运用勾股定理,通过作直角三角形,
画出了长度为无理数的线段,并学习在数轴上画出
无理数表示的点的方法.课件说明课件说明学习目标:
1.能用勾股定理证明直角三角形全等的“斜边、
直角边”判定定理;
2.能应用勾股定理在数轴上画出表示无理数的点;
3.体会勾股定理在数学中的地位和作用.
学习重点:
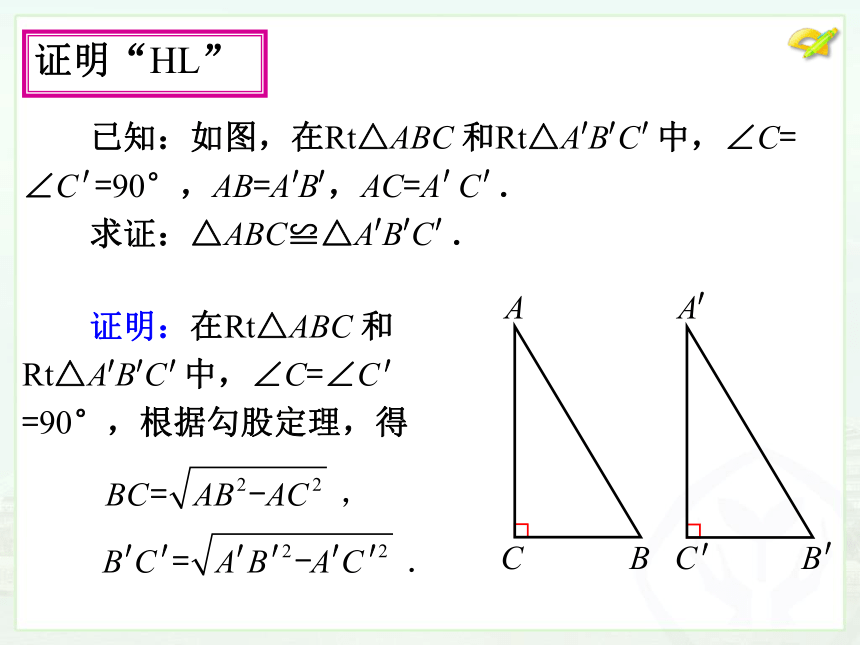
用勾股定理作出长度为无理数的线段. 问题1 在八年级上册中,我们曾经通过画图得到结
论:斜边和一条直角边分别相等的两个直角三角形全等.
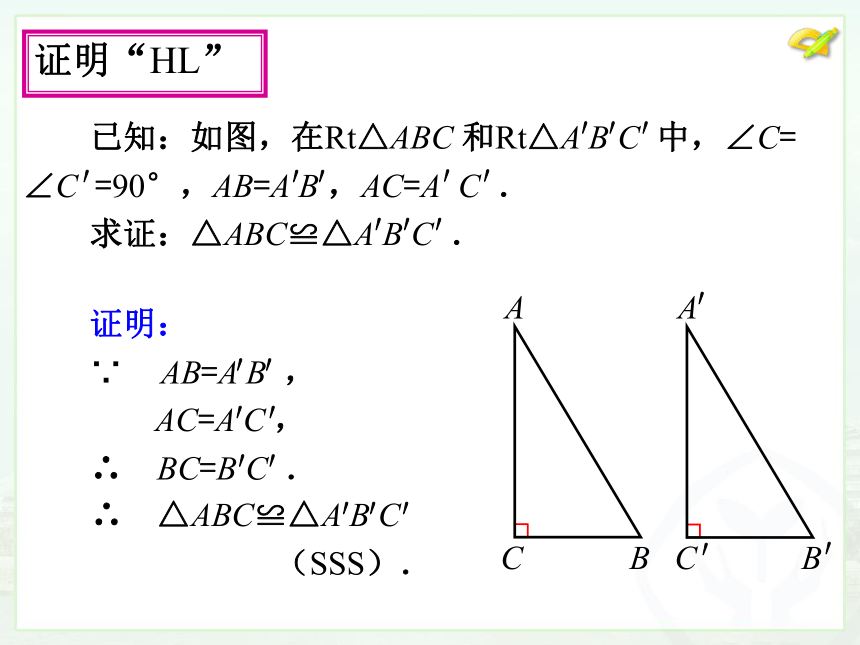
学习了勾股定理后,你能证明这一结论吗?证明“HL” 证明“HL” 证明“HL” ′′′′′′ 证明:
∵ AB=A B ,
AC=A C ,
∴ BC=B C .画图提高 问题2 我们知道数轴上的点有的表示有理数,有
的表示无理数,你能在数轴上画出表示 的点吗?画图提高 练习1 教科书第27页练习1. “数学海螺” 类比迁移 应用提高 例 如图,△ACB和△ECD都是等腰直角三角形,
∠ACB =∠ECD =90°,D为AB边上一点.求证:AD2 +
DB2 =DE2. 证明:∵ ∠ACB =∠ECD,
∴ ∠ACD +∠BCD=∠ACD +∠ACE ,
∴ ∠BCD =∠ACE.
又 BC=AC, DC=EC,
∴ △ACE≌△BCD.应用提高 证明:∴ ∠B =∠CAE=45°,
∠DAE =∠CAE+∠BAC
=45°+45°=90°.
∴ AD2 +AE2 =DE2.
∵ AE=DB ,
∴ AD2 +DB2 =DE2. 例 如图,△ACB和△ECD都是等腰直角三角形,
∠ACB =∠ECD =90°,D为AB边上一点.求证:AD2 +
DB2 =DE2.应用提高 练习2 教科书第27页练习2. (1)勾股定理有哪些方面的应用,本节课学习了勾
股定理哪几方面的应用?
(2)你能说说勾股定理求线段长的基本思路吗?
(3)本节课体现出哪些数学思想方法?课堂小结 作业:教科书第27页第1,2题. 课后作业
判定定理,从中进一步确认,一个直角三角形中,
只要两边的大小确定,则这个三角形就形状大小就
确定了.然后,运用勾股定理,通过作直角三角形,
画出了长度为无理数的线段,并学习在数轴上画出
无理数表示的点的方法.课件说明课件说明学习目标:
1.能用勾股定理证明直角三角形全等的“斜边、
直角边”判定定理;
2.能应用勾股定理在数轴上画出表示无理数的点;
3.体会勾股定理在数学中的地位和作用.
学习重点:
用勾股定理作出长度为无理数的线段. 问题1 在八年级上册中,我们曾经通过画图得到结
论:斜边和一条直角边分别相等的两个直角三角形全等.
学习了勾股定理后,你能证明这一结论吗?证明“HL” 证明“HL” 证明“HL” ′′′′′′ 证明:
∵ AB=A B ,
AC=A C ,
∴ BC=B C .画图提高 问题2 我们知道数轴上的点有的表示有理数,有
的表示无理数,你能在数轴上画出表示 的点吗?画图提高 练习1 教科书第27页练习1. “数学海螺” 类比迁移 应用提高 例 如图,△ACB和△ECD都是等腰直角三角形,
∠ACB =∠ECD =90°,D为AB边上一点.求证:AD2 +
DB2 =DE2. 证明:∵ ∠ACB =∠ECD,
∴ ∠ACD +∠BCD=∠ACD +∠ACE ,
∴ ∠BCD =∠ACE.
又 BC=AC, DC=EC,
∴ △ACE≌△BCD.应用提高 证明:∴ ∠B =∠CAE=45°,
∠DAE =∠CAE+∠BAC
=45°+45°=90°.
∴ AD2 +AE2 =DE2.
∵ AE=DB ,
∴ AD2 +DB2 =DE2. 例 如图,△ACB和△ECD都是等腰直角三角形,
∠ACB =∠ECD =90°,D为AB边上一点.求证:AD2 +
DB2 =DE2.应用提高 练习2 教科书第27页练习2. (1)勾股定理有哪些方面的应用,本节课学习了勾
股定理哪几方面的应用?
(2)你能说说勾股定理求线段长的基本思路吗?
(3)本节课体现出哪些数学思想方法?课堂小结 作业:教科书第27页第1,2题. 课后作业
