19.2.2 一次函数(2)
文档属性
| 名称 | 19.2.2 一次函数(2) |  | |
| 格式 | zip | ||
| 文件大小 | 600.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-12 09:52:17 | ||
图片预览






文档简介
课件19张PPT。八年级 下册19.2.2 一次函数(2)本课是在学习一次函数概念的基础上,研究它的图
象和性质.研究一次函数的图象和性质,重点是让
学生概括当k >0和k <0时,一次函数y = kx+b 图象
的特征,随着自变量x 的变化,函数值y 怎样变化.
通过一次函数图象性质的研究,体会数形结合的思
想.课件说明学习目标:
1.会画一次函数的图象;
2.能从图象角度理解正比例函数与一次函数的关
系;
3.能根据一次函数的图象和表达式y =kx+b(k≠0)
理解k>0和k<0时,图象的变化情况. 从而理
解一次函数的增减性;课件说明课件说明 4.通过观察图象、类比正比例函数性质概括一次
函数性质的活动,发展数学感知、数学表征、
数学概括能力,体会数形结合的思想,发展几
何直观.
学习重点:
用数形结合的思想方法,通过画图观察,概括一次
函数的性质. (1)什么是一次函数?请写出三个一次函数的解
析式.
(2)什么叫正比例函数?从解析式看,正比例函
数与一次函数有什么关系?
(3)正比例函数有哪些性质?是怎样得到这些性
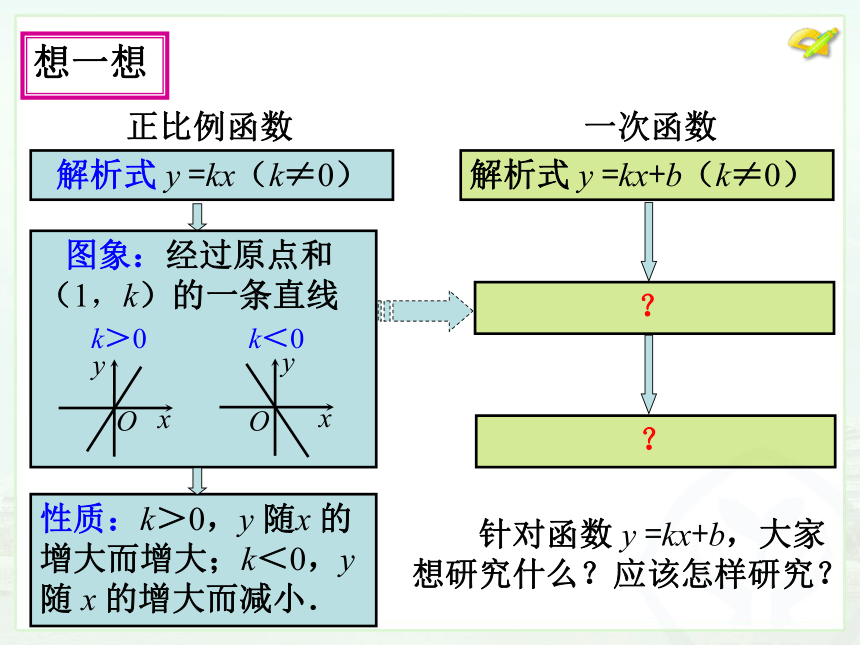
质的?想一想想一想正比例函数 解析式 y =kx(k≠0) 性质:k>0,y 随x 的增大而增大;k<0,y 随 x 的增大而减小.一次函数解析式 y =kx+b(k≠0) 针对函数 y =kx+b,大家想研究什么?应该怎样研究? 研究函数 y =kx+b(k≠0)的性质;
研究方法:
画图象→观察图象→变量(坐标)意义解释.2-2-4-6-55xyO画一画 画一次函数 y =2x-3 的图象. 画出坐标系中满足函数关系的两点;
过这两点画直线.想一想(1)一次函数 y =2x-3 的图象是什么形状?
(2)一次函数 y =kx+b(k≠0)的图象是什么形状?它
与 y =kx 的图象有什么位置关系?
(3)我们知道,两点确定一条直线,由此能否更简便
地画出一次函数的图象?怎样画? 仿照正比例函数的做
法,你能看出当 k 的符号
变化时,函数的增减性怎
样变化?做一做 请用简便方法画出下列一次函数的图象:
(1)y =x+1; (2)y =3x+1;
(3)y =-x+1; (4)y =-3x+1. k>0时,直线左低
右高,y 随x 的增大而增
大;
k<0时,直线左高
右低,y 随x 的增大而减
小.做一做 请用简便方法画出下列一次函数的图象:
(1)y =x+1; (2)y =3x+1;
(3)y =-x+1; (4)y =-3x+1. 练一练(0,-3)一、三、四增大 练习1 直线y =2x-3 与x 轴交点的坐标为________;
与y 轴交点的坐标为________;图象经过____________
象限, y 随x 的增大而________.(1.5,0)练一练 练习2 在同一直角坐标系中画出下列函数的图象,
每小题中三个函数图象有什么关系?
(1)y =x-1,y =x,y =x+1;
(2)y =-2x-1,y =-2x,y =-2x+1.练一练 练习3 在同一坐标系中画出下列函数的图象,并
指出它们的共同之处.练一练 练习4 一次函数 y =kx+b,y 随 x 的增大而减小,b
>0,则它的图象经过第____________象限.一、二、四练一练 练习5 如下图是函数 y = 的图象,
请说说这个函数的最小值是多少,并说明理由.31xyO12234 (1)一次函数 y =kx+b(k≠0)的图象是什么形状?
怎样用简便方法画出一个一次函数的图象?
(2)一次函数有哪些性质?一次函数与正比例函数
有什么关系?
(3)我们是怎样对一次函数的性质进行研究的?课堂小结y=kx+b(k≠0) y=kx(k≠0)图象
平移 k>0时,直线左低右高,y 随x 的增大而增大;
k<0时,直线左高右低,y 随x 的增大而减小. 两点法画一
次函数图象 研究方法:
画图象箭头→观察图象→变量(坐标)意义解释.课堂小结 作业:教科书第99~100页习题19.2第4,5,9,12,14 题.课后作业
象和性质.研究一次函数的图象和性质,重点是让
学生概括当k >0和k <0时,一次函数y = kx+b 图象
的特征,随着自变量x 的变化,函数值y 怎样变化.
通过一次函数图象性质的研究,体会数形结合的思
想.课件说明学习目标:
1.会画一次函数的图象;
2.能从图象角度理解正比例函数与一次函数的关
系;
3.能根据一次函数的图象和表达式y =kx+b(k≠0)
理解k>0和k<0时,图象的变化情况. 从而理
解一次函数的增减性;课件说明课件说明 4.通过观察图象、类比正比例函数性质概括一次
函数性质的活动,发展数学感知、数学表征、
数学概括能力,体会数形结合的思想,发展几
何直观.
学习重点:
用数形结合的思想方法,通过画图观察,概括一次
函数的性质. (1)什么是一次函数?请写出三个一次函数的解
析式.
(2)什么叫正比例函数?从解析式看,正比例函
数与一次函数有什么关系?
(3)正比例函数有哪些性质?是怎样得到这些性
质的?想一想想一想正比例函数 解析式 y =kx(k≠0) 性质:k>0,y 随x 的增大而增大;k<0,y 随 x 的增大而减小.一次函数解析式 y =kx+b(k≠0) 针对函数 y =kx+b,大家想研究什么?应该怎样研究? 研究函数 y =kx+b(k≠0)的性质;
研究方法:
画图象→观察图象→变量(坐标)意义解释.2-2-4-6-55xyO画一画 画一次函数 y =2x-3 的图象. 画出坐标系中满足函数关系的两点;
过这两点画直线.想一想(1)一次函数 y =2x-3 的图象是什么形状?
(2)一次函数 y =kx+b(k≠0)的图象是什么形状?它
与 y =kx 的图象有什么位置关系?
(3)我们知道,两点确定一条直线,由此能否更简便
地画出一次函数的图象?怎样画? 仿照正比例函数的做
法,你能看出当 k 的符号
变化时,函数的增减性怎
样变化?做一做 请用简便方法画出下列一次函数的图象:
(1)y =x+1; (2)y =3x+1;
(3)y =-x+1; (4)y =-3x+1. k>0时,直线左低
右高,y 随x 的增大而增
大;
k<0时,直线左高
右低,y 随x 的增大而减
小.做一做 请用简便方法画出下列一次函数的图象:
(1)y =x+1; (2)y =3x+1;
(3)y =-x+1; (4)y =-3x+1. 练一练(0,-3)一、三、四增大 练习1 直线y =2x-3 与x 轴交点的坐标为________;
与y 轴交点的坐标为________;图象经过____________
象限, y 随x 的增大而________.(1.5,0)练一练 练习2 在同一直角坐标系中画出下列函数的图象,
每小题中三个函数图象有什么关系?
(1)y =x-1,y =x,y =x+1;
(2)y =-2x-1,y =-2x,y =-2x+1.练一练 练习3 在同一坐标系中画出下列函数的图象,并
指出它们的共同之处.练一练 练习4 一次函数 y =kx+b,y 随 x 的增大而减小,b
>0,则它的图象经过第____________象限.一、二、四练一练 练习5 如下图是函数 y = 的图象,
请说说这个函数的最小值是多少,并说明理由.31xyO12234 (1)一次函数 y =kx+b(k≠0)的图象是什么形状?
怎样用简便方法画出一个一次函数的图象?
(2)一次函数有哪些性质?一次函数与正比例函数
有什么关系?
(3)我们是怎样对一次函数的性质进行研究的?课堂小结y=kx+b(k≠0) y=kx(k≠0)图象
平移 k>0时,直线左低右高,y 随x 的增大而增大;
k<0时,直线左高右低,y 随x 的增大而减小. 两点法画一
次函数图象 研究方法:
画图象箭头→观察图象→变量(坐标)意义解释.课堂小结 作业:教科书第99~100页习题19.2第4,5,9,12,14 题.课后作业
