第19章 数学活动
图片预览





文档简介
课件12张PPT。八年级 下册第19章 数学活动本课是数学活动,初步学习用函数模拟方法研究问
题,即在不知道某一运动变化过程可以用什么类型
函数刻画的情况下,取变量的几对对应值,在平面
直角坐标系中画出相应的点,看看与哪类函数比较
接近,然后设函数式,确定系数,求出函数式,再
研究其变化规律.课件说明学习目标:
1.会根据两个变量的部分对应值建立函数模型;
2.会用一次函数模型描述和研究实际问题中的运动
变化规律;
3.经历根据两个变量的部分对应数据建立函数模型
的过程,体会函数建型过程中的归纳思想、数形
结合思想;初步体会函数模拟思想.课件说明课件说明学习重点:
根据两个变量的部分对应值建立函数模型,初步体
会函数模拟的思想方法. 一个水龙头漏水,有人认为漏这一点水没有什么大
不了,你也这样认为吗?
为了估计一个水龙头一个月(30 天)漏水量、一年
(365 天)漏水量,大家在课前进行了必要的数据收集,
现在请各研究小组展示自己获得的数据. 为了估计一月和一年的漏水量,我们能收集该水龙
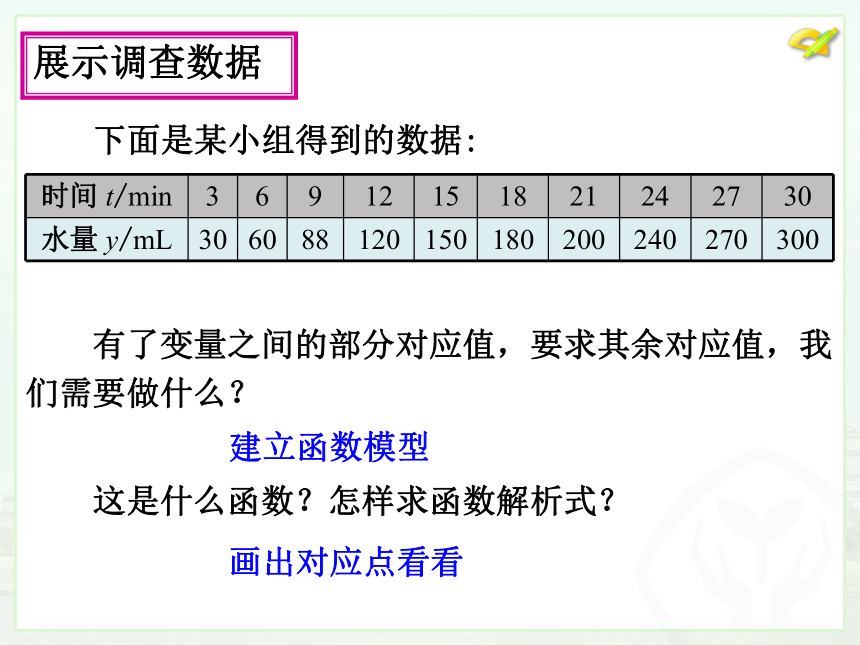
头一个月和一年的漏水量吗?这样做可行吗?展示调查数据 有了变量之间的部分对应值,要求其余对应值,我
们需要做什么?
这是什么函数?怎样求函数解析式?
建立函数模型画出对应点看看 展示调查数据 下面是某小组得到的数据:做一做 请在平面直角坐标系中画出相应的点.近似于正比例函数 从图象上看,这个函数应该
是什么函数?
能求出这个函数的解析式吗?做一做 当t =30 天= 30×24×60
= 43 200 min 时,
y = 432 000 mL,一个月
漏掉432 kg 水;
当t = 365 天= 525 600 min
时,
y = 5 256 000 mL,一年漏
掉5 256 kg 水. (1)收集到的数据不同;
(2)函数解析式不符合实际情况;
(3)计算错误(包括时间和漏水量单位换算错误).想一想 各小组通过努力,解决了问题,发现滴水之漏,随
着时间累积,浪费巨大.刚才交流过程中,各小组得到
的函数解析式不尽相同,结果也不尽相同,为什么? 收集数据→画散点图→选择函数→求函数式(待定
系数)→得到结论→检验 想一想 怎样检验得到的函数解析式是否符合实际意义 ?
解决这个问题分哪几步进行?做一做 (1)根据下表数据,在平面直角坐标系中画出世界
人口增长曲线图;
(2)选择一个近似于人口增长曲线的一次函数,写
出它的函数解析式;
(3)按照这样的增长趋势,估计2020 年的世界人口
总数.课堂小结 本课我们解决了一类新问题,请带着下面问题总结经验:
(1)这一类新问题有什么特点?
(2)怎样解决这类问题?分了哪些步骤?
(3)从这类问题的解决过程中,你对应用函数解决
问题有哪些体会? 收集数据→画散点图→选择函数→求函数式(待定
系数) →得到结论→检验
题,即在不知道某一运动变化过程可以用什么类型
函数刻画的情况下,取变量的几对对应值,在平面
直角坐标系中画出相应的点,看看与哪类函数比较
接近,然后设函数式,确定系数,求出函数式,再
研究其变化规律.课件说明学习目标:
1.会根据两个变量的部分对应值建立函数模型;
2.会用一次函数模型描述和研究实际问题中的运动
变化规律;
3.经历根据两个变量的部分对应数据建立函数模型
的过程,体会函数建型过程中的归纳思想、数形
结合思想;初步体会函数模拟思想.课件说明课件说明学习重点:
根据两个变量的部分对应值建立函数模型,初步体
会函数模拟的思想方法. 一个水龙头漏水,有人认为漏这一点水没有什么大
不了,你也这样认为吗?
为了估计一个水龙头一个月(30 天)漏水量、一年
(365 天)漏水量,大家在课前进行了必要的数据收集,
现在请各研究小组展示自己获得的数据. 为了估计一月和一年的漏水量,我们能收集该水龙
头一个月和一年的漏水量吗?这样做可行吗?展示调查数据 有了变量之间的部分对应值,要求其余对应值,我
们需要做什么?
这是什么函数?怎样求函数解析式?
建立函数模型画出对应点看看 展示调查数据 下面是某小组得到的数据:做一做 请在平面直角坐标系中画出相应的点.近似于正比例函数 从图象上看,这个函数应该
是什么函数?
能求出这个函数的解析式吗?做一做 当t =30 天= 30×24×60
= 43 200 min 时,
y = 432 000 mL,一个月
漏掉432 kg 水;
当t = 365 天= 525 600 min
时,
y = 5 256 000 mL,一年漏
掉5 256 kg 水. (1)收集到的数据不同;
(2)函数解析式不符合实际情况;
(3)计算错误(包括时间和漏水量单位换算错误).想一想 各小组通过努力,解决了问题,发现滴水之漏,随
着时间累积,浪费巨大.刚才交流过程中,各小组得到
的函数解析式不尽相同,结果也不尽相同,为什么? 收集数据→画散点图→选择函数→求函数式(待定
系数)→得到结论→检验 想一想 怎样检验得到的函数解析式是否符合实际意义 ?
解决这个问题分哪几步进行?做一做 (1)根据下表数据,在平面直角坐标系中画出世界
人口增长曲线图;
(2)选择一个近似于人口增长曲线的一次函数,写
出它的函数解析式;
(3)按照这样的增长趋势,估计2020 年的世界人口
总数.课堂小结 本课我们解决了一类新问题,请带着下面问题总结经验:
(1)这一类新问题有什么特点?
(2)怎样解决这类问题?分了哪些步骤?
(3)从这类问题的解决过程中,你对应用函数解决
问题有哪些体会? 收集数据→画散点图→选择函数→求函数式(待定
系数) →得到结论→检验
