16.3 分式方程 第1课时
图片预览






文档简介
课件23张PPT。 黔江区舟白中学
E-Mail:416352289@qq.com分式方程
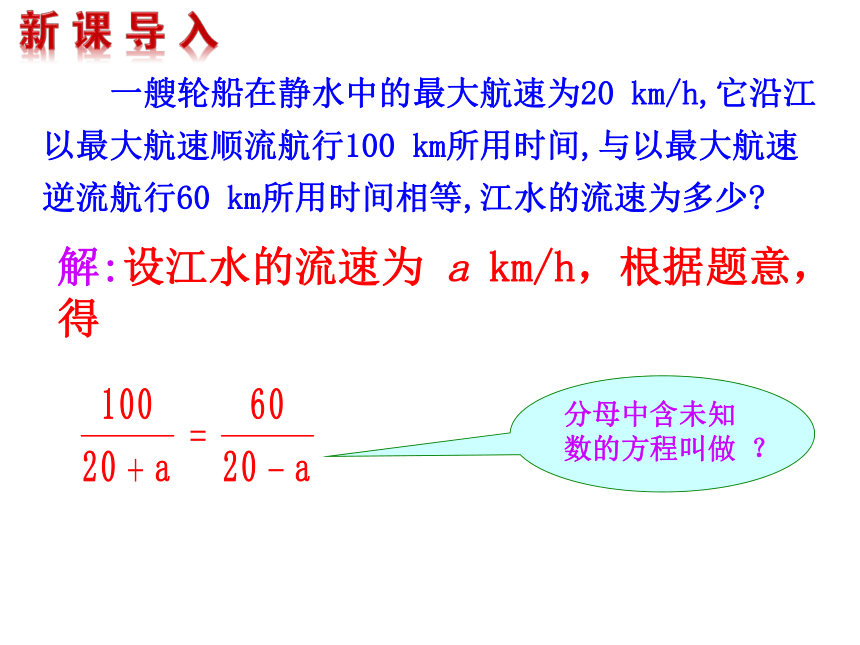
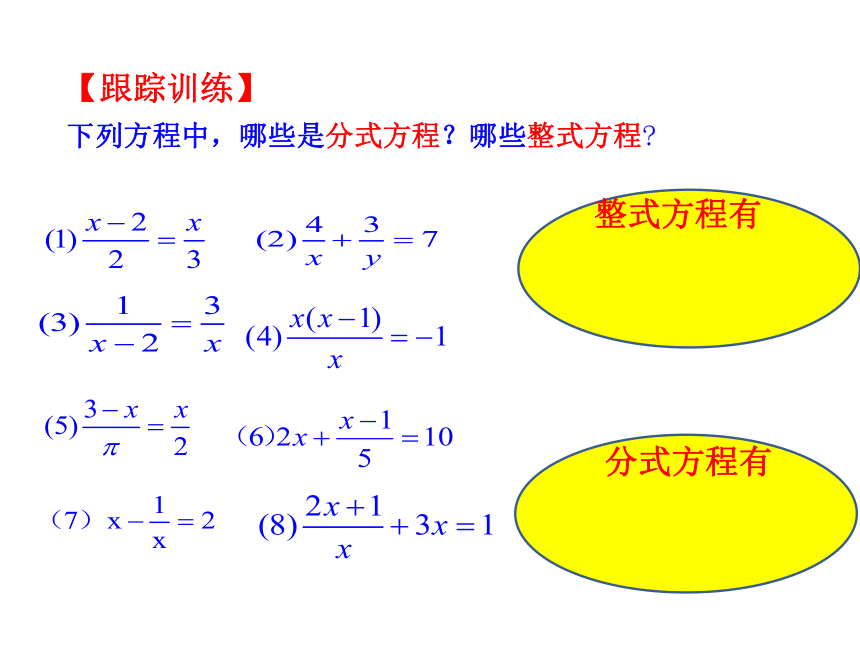
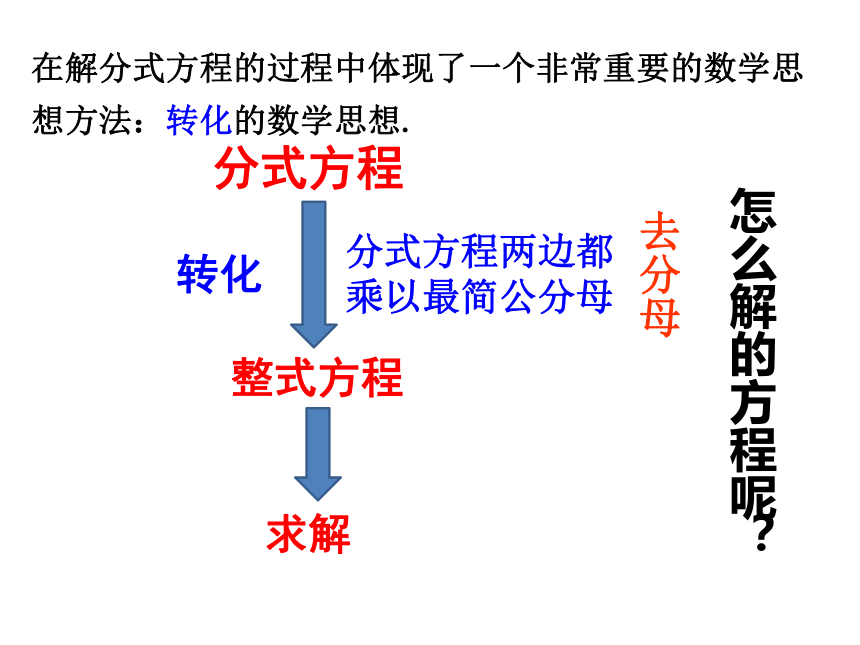
第1课时 一艘轮船在静水中的最大航速为20 km/h,它沿江以最大航速顺流航行100 km所用时间,与以最大航速逆流航行60 km所用时间相等,江水的流速为多少?解:设江水的流速为 a km/h,根据题意,得分母中含未知数的方程叫做 ?像这样以前学过的分母里不含有未知数的方程叫做整式方程.分母中含有未知数的方程叫做分式方程. 下列方程中,哪些是分式方程?哪些整式方程?【跟踪训练】整式方程有分式方程有a=5下面我们一起研究怎么样来解分式方程:方程两边同乘以最简公分母(20+a)(20-a),检验:将a=5代入分式方程,左边=4=右边,100(20-a)=60(20+a)得解得 ∴ a=5 是原分式方程的解.分式方程整式方程在解分式方程的过程中体现了一个非常重要的数学思想方法:转化的数学思想.分式方程整式方程转化求解分式方程两边都
乘以最简公分母怎么解的方程呢?去分母【例题】解方程:解:方程两边都乘以 x (x-3) 得2x=3(x-3)X=9解得检验:当x=9时,x(x-3)≠0x=9 是原方程的解∴最简公分母整式方程(去分母)解方程:解:去分母得解得检验: 当 时,X(x+1)≠0是原分式方程的解∴解分式方程:解:方程两边同乘以 (x-5)(x+5) 得,x+5=10解得x=5当x=5时,(x-5)(x+5)= 0,原分式方程无解.为什么会产生曾根?x=5 是原分式方程的∴∴检验:最简公分母整式方程(去分母得)增根.所以我们解完分式方程时一定要代入原分式方程或最简公分母进行产生的原因:分式方程两边同乘一个为零的因式后,所得的根是整式方程的根,而不是分式方程的根.(分母为0无意义)检验.例 解方程:解:去分母得x(x+2)-(x-1)(x+2)=3X=1解得检验:当x=1时,(x-1)(x+2)=0,原分式方程无解∴舍去解分式方程的一般步骤:1.在方程的两边都乘最简公分母,约去分母,化成整式方程.
2.解这个整式方程.
3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4.写出原方程的解.解分式方程的思路:分式方程整式方程去分母“一化二解三检验”求解检验解分式方程容易犯的错误有:(1) 去分母时,原方程的整式部分漏乘.(2) 约去分母后,分子是多项式时, 没有添括号.(因分数线有括号的作用) (3) 把整式方程的解代入最简公分母后的值为0,不舍掉.
若分式 与1互为相反数,则x的
值是______.
【解析】由题意得 =-1
∴-x+1=2
∴x=-1
当x=-1时,x-1≠0.
答案:-1-1 点A,B在数轴上所对应的数分别是-3和 且点A,B到原点的距离相等,求x的值.解:由题意得, 解得:经检验, 是原方程的解. 如果关于x的方程 无解,则m的值等于( )
A.-3 B.-2 C.-1 D.3方程的两边都乘(x-3),得 2=x-3-m,即 x=5+m,由于方程无解, 即5+m=3,∴m=-2.【解析】∴ x=3,B 关于x的方程 无解,求k的值.解:方程的两边同时乘(x+3)(x-3)得x+3+kx-3k=k+3整理得: (k+1)x=4k∵ 方程无解,则x=3或x=-3① 当x=3时,(k+1) ·3=4k, ∴ k=3,②当x=-3时,(k+1)(-3)=4k, ∴所以当k=3或 时,原分式方程无解. 知识拓展-3-1-5≦-1且a≠-2m<8且m≠2X=2解方程:(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)通过本课时的学习,需要我们
1.理解分式方程的概念和分式方程产生无解的原因 ,会辨别整式方程与分式方程.
2.掌握分式方程的解法,会解可化为一元一次方程的分式方程 .
解分式方程的一般步骤:
①去分母,将分式方程转化为整式方程;
②解整式方程;
③验根作答. 作业布置
同步练习册
第1课时 一艘轮船在静水中的最大航速为20 km/h,它沿江以最大航速顺流航行100 km所用时间,与以最大航速逆流航行60 km所用时间相等,江水的流速为多少?解:设江水的流速为 a km/h,根据题意,得分母中含未知数的方程叫做 ?像这样以前学过的分母里不含有未知数的方程叫做整式方程.分母中含有未知数的方程叫做分式方程. 下列方程中,哪些是分式方程?哪些整式方程?【跟踪训练】整式方程有分式方程有a=5下面我们一起研究怎么样来解分式方程:方程两边同乘以最简公分母(20+a)(20-a),检验:将a=5代入分式方程,左边=4=右边,100(20-a)=60(20+a)得解得 ∴ a=5 是原分式方程的解.分式方程整式方程在解分式方程的过程中体现了一个非常重要的数学思想方法:转化的数学思想.分式方程整式方程转化求解分式方程两边都
乘以最简公分母怎么解的方程呢?去分母【例题】解方程:解:方程两边都乘以 x (x-3) 得2x=3(x-3)X=9解得检验:当x=9时,x(x-3)≠0x=9 是原方程的解∴最简公分母整式方程(去分母)解方程:解:去分母得解得检验: 当 时,X(x+1)≠0是原分式方程的解∴解分式方程:解:方程两边同乘以 (x-5)(x+5) 得,x+5=10解得x=5当x=5时,(x-5)(x+5)= 0,原分式方程无解.为什么会产生曾根?x=5 是原分式方程的∴∴检验:最简公分母整式方程(去分母得)增根.所以我们解完分式方程时一定要代入原分式方程或最简公分母进行产生的原因:分式方程两边同乘一个为零的因式后,所得的根是整式方程的根,而不是分式方程的根.(分母为0无意义)检验.例 解方程:解:去分母得x(x+2)-(x-1)(x+2)=3X=1解得检验:当x=1时,(x-1)(x+2)=0,原分式方程无解∴舍去解分式方程的一般步骤:1.在方程的两边都乘最简公分母,约去分母,化成整式方程.
2.解这个整式方程.
3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4.写出原方程的解.解分式方程的思路:分式方程整式方程去分母“一化二解三检验”求解检验解分式方程容易犯的错误有:(1) 去分母时,原方程的整式部分漏乘.(2) 约去分母后,分子是多项式时, 没有添括号.(因分数线有括号的作用) (3) 把整式方程的解代入最简公分母后的值为0,不舍掉.
若分式 与1互为相反数,则x的
值是______.
【解析】由题意得 =-1
∴-x+1=2
∴x=-1
当x=-1时,x-1≠0.
答案:-1-1 点A,B在数轴上所对应的数分别是-3和 且点A,B到原点的距离相等,求x的值.解:由题意得, 解得:经检验, 是原方程的解. 如果关于x的方程 无解,则m的值等于( )
A.-3 B.-2 C.-1 D.3方程的两边都乘(x-3),得 2=x-3-m,即 x=5+m,由于方程无解, 即5+m=3,∴m=-2.【解析】∴ x=3,B 关于x的方程 无解,求k的值.解:方程的两边同时乘(x+3)(x-3)得x+3+kx-3k=k+3整理得: (k+1)x=4k∵ 方程无解,则x=3或x=-3① 当x=3时,(k+1) ·3=4k, ∴ k=3,②当x=-3时,(k+1)(-3)=4k, ∴所以当k=3或 时,原分式方程无解. 知识拓展-3-1-5≦-1且a≠-2m<8且m≠2X=2解方程:(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)通过本课时的学习,需要我们
1.理解分式方程的概念和分式方程产生无解的原因 ,会辨别整式方程与分式方程.
2.掌握分式方程的解法,会解可化为一元一次方程的分式方程 .
解分式方程的一般步骤:
①去分母,将分式方程转化为整式方程;
②解整式方程;
③验根作答. 作业布置
同步练习册
