二倍角的三角函数公式第2课时课件1(共24张PPT)2022-2023学年高一下学期数学北师大版(2019)必修第二册
文档属性
| 名称 | 二倍角的三角函数公式第2课时课件1(共24张PPT)2022-2023学年高一下学期数学北师大版(2019)必修第二册 |

|
|
| 格式 | zip | ||
| 文件大小 | 787.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-07 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
二倍角的三角函数公式
第2课时
新知探究
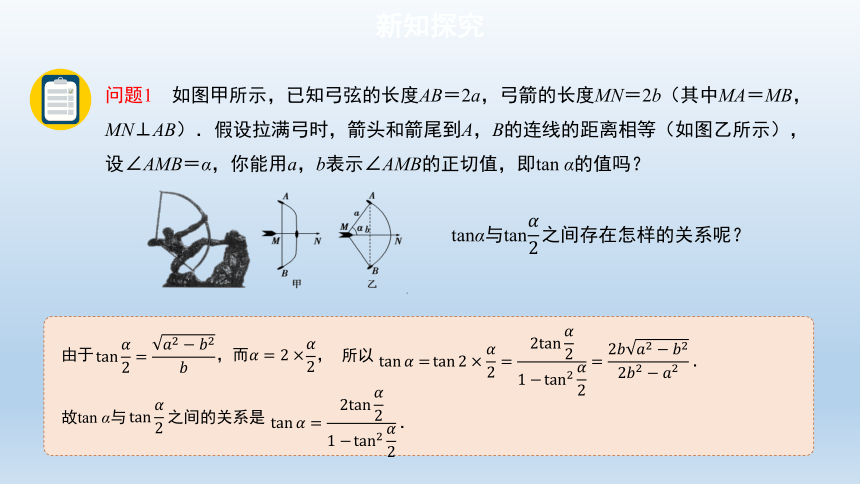
问题1 如图甲所示,已知弓弦的长度AB=2a,弓箭的长度MN=2b(其中MA=MB,MN⊥AB).假设拉满弓时,箭头和箭尾到A,B的连线的距离相等(如图乙所示),设∠AMB=α,你能用a,b表示∠AMB的正切值,即tan α的值吗?
tanα与tan 之间存在怎样的关系呢?
由于 ,而 ,
所以
故tan α与 之间的关系是
新知探究
问题2 α与 是什么关系?
倍角关系,α是 的二倍.
新知探究
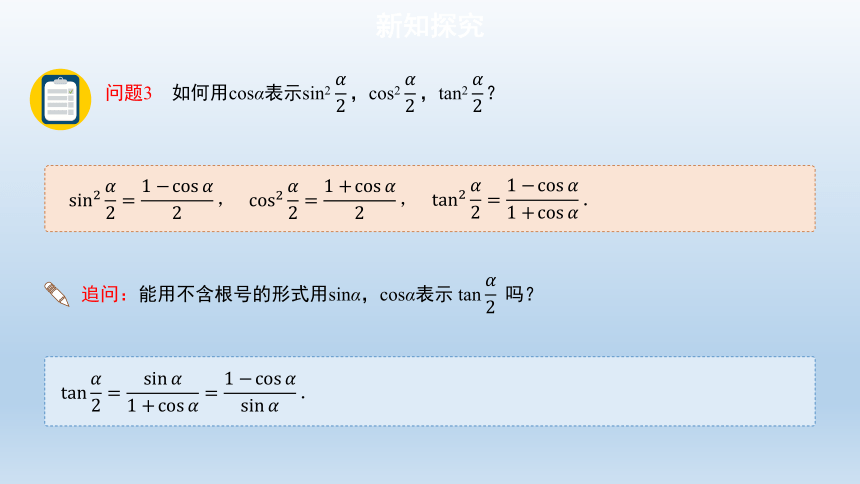
问题3 如何用cosα表示sin2 ,cos2 ,tan2 ?
追问:能用不含根号的形式用sinα,cosα表示 tan 吗?
新知探究
问题4 根据上述探究写出二倍角公式?
(1)
(2)
(3)
新知探究
问题5 如何用tan 表示sinα,cosα,tanα?
新知探究
问题6 已知 ,450°<α<540°,求 的值.
由题意得
∵450°<α<540°,∴cos α= ,
∴
即1-sin α= ,得sin α= .
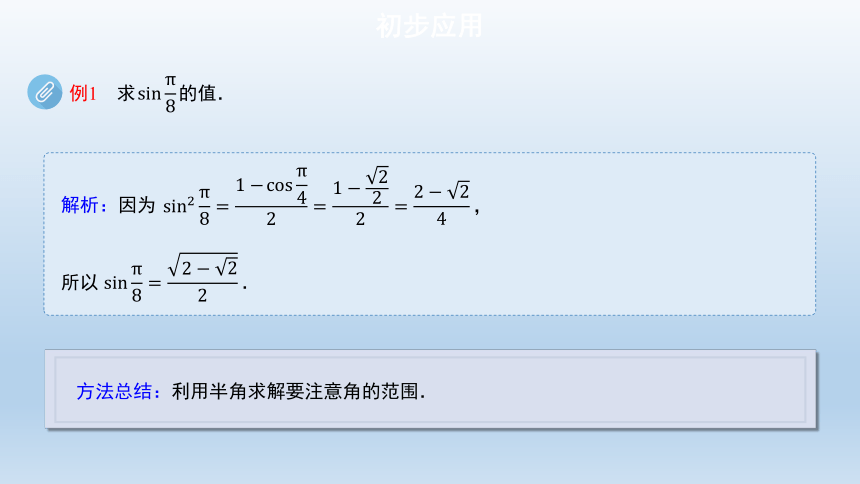
例1 求 的值.
初步应用
方法总结:利用半角求解要注意角的范围.
解析:因为
所以
例2 已知 ,求 .
初步应用
方法总结:已知三角函数式的值,求其他三角函数式的值.一般思路为,观察已知条件与所求式子之间的联系(从三角函数名及角入手),再将已知条件代入所求式子,化简求值.
解析:因为
又因为 ,故
所以
例3 (1)计算:
初步应用
(2)化简 (-π<α<0).
例3 (1)计算:
初步应用
(2)化简 (-π<α<0).
(1)法1:
解析:
例3 (1)计算:
初步应用
(2)化简 (-π<α<0).
(1)法2:
例3 (1)计算:
初步应用
(2)化简 (-π<α<0).
(2)原式
例3 (1)计算:
初步应用
(2)化简 (-π<α<0).
解析:因为-π<α<0,所以
所以 <0,故原式= =cos α.
初步应用
(1)题中两种不同方法实质是运用了不同的半角的正切公式.
(2)利用公式 ,需要注意 范围.
法1:
法2:
归纳小结
(1)利用半角公式求值的思路是什么?
(2)半角的正切公式的表达式有几种?
问题7 回归本节的学习,你有什么收获?可以从以下几个问题归纳.
(1)已知三角函数式的值,求其他三角函数式的值,一般思路为:
①先化简已知或所求式子;
②观察已知条件与所求式子之间的联系(从三角函数名及角入手);
③将已知条件代入所求式子,化简求值.
归纳小结
(1)利用半角公式求值的思路是什么?
(2)半角的正切公式的表达式有几种?
问题7 回归本节的学习,你有什么收获?可以从以下几个问题归纳.
(2)半角的正切公式分无理表达式与有理表达式两种形式,
前者有正负号选取,其符号由角的范围确定,必要时需要讨论,
后者没有符号选取,其结果的符号由sin α确定,应用十分方便.
作业布置
作业:教科书P158页,A组第6,7,8,10题,B组第4题.
目标检测
A.
C.
D.
B.
1
若sin(π-α)= 且α∈ ,则 等于( )
解析:由题意知sinα= ,α∈ ,
所以
所以
B
目标检测
A.
C.
D.
B.8
2
若f(x)=2tanx- ,则 的值是( )
解析:
又
故
B
目标检测
3
已知 ,540°<α<720°,则 =________.
解析:因为540°<α<720°,所以270°< <360°,
所以135°< <180°.
因为 ,所以
目标检测
4
已知sinφ= ,且φ是第三象限角,求下列各三角函数的值:
(1) ;(2)sin 2φ;(3) ;(4) .
解析:因为φ是第三象限角,所以cosφ=
(1)
(2)sin2φ=2sinφcosφ= .
目标检测
4
已知sin φ= ,且φ是第三象限角,求下列各三角函数的值:
(1) ;(2)sin 2φ;(3) ;(4) .
(3)因为φ是第三象限角,所以2kπ+π<φ<2kπ+ ,
所以 (k∈Z).
当k=2m时, (m∈Z),
当k=2m+1时, (m∈Z),
目标检测
4
已知sin φ= ,且φ是第三象限角,求下列各三角函数的值:
(1) ;(2)sin 2φ;(3) ;(4) .
(4)
二倍角的三角函数公式
第2课时
新知探究
问题1 如图甲所示,已知弓弦的长度AB=2a,弓箭的长度MN=2b(其中MA=MB,MN⊥AB).假设拉满弓时,箭头和箭尾到A,B的连线的距离相等(如图乙所示),设∠AMB=α,你能用a,b表示∠AMB的正切值,即tan α的值吗?
tanα与tan 之间存在怎样的关系呢?
由于 ,而 ,
所以
故tan α与 之间的关系是
新知探究
问题2 α与 是什么关系?
倍角关系,α是 的二倍.
新知探究
问题3 如何用cosα表示sin2 ,cos2 ,tan2 ?
追问:能用不含根号的形式用sinα,cosα表示 tan 吗?
新知探究
问题4 根据上述探究写出二倍角公式?
(1)
(2)
(3)
新知探究
问题5 如何用tan 表示sinα,cosα,tanα?
新知探究
问题6 已知 ,450°<α<540°,求 的值.
由题意得
∵450°<α<540°,∴cos α= ,
∴
即1-sin α= ,得sin α= .
例1 求 的值.
初步应用
方法总结:利用半角求解要注意角的范围.
解析:因为
所以
例2 已知 ,求 .
初步应用
方法总结:已知三角函数式的值,求其他三角函数式的值.一般思路为,观察已知条件与所求式子之间的联系(从三角函数名及角入手),再将已知条件代入所求式子,化简求值.
解析:因为
又因为 ,故
所以
例3 (1)计算:
初步应用
(2)化简 (-π<α<0).
例3 (1)计算:
初步应用
(2)化简 (-π<α<0).
(1)法1:
解析:
例3 (1)计算:
初步应用
(2)化简 (-π<α<0).
(1)法2:
例3 (1)计算:
初步应用
(2)化简 (-π<α<0).
(2)原式
例3 (1)计算:
初步应用
(2)化简 (-π<α<0).
解析:因为-π<α<0,所以
所以 <0,故原式= =cos α.
初步应用
(1)题中两种不同方法实质是运用了不同的半角的正切公式.
(2)利用公式 ,需要注意 范围.
法1:
法2:
归纳小结
(1)利用半角公式求值的思路是什么?
(2)半角的正切公式的表达式有几种?
问题7 回归本节的学习,你有什么收获?可以从以下几个问题归纳.
(1)已知三角函数式的值,求其他三角函数式的值,一般思路为:
①先化简已知或所求式子;
②观察已知条件与所求式子之间的联系(从三角函数名及角入手);
③将已知条件代入所求式子,化简求值.
归纳小结
(1)利用半角公式求值的思路是什么?
(2)半角的正切公式的表达式有几种?
问题7 回归本节的学习,你有什么收获?可以从以下几个问题归纳.
(2)半角的正切公式分无理表达式与有理表达式两种形式,
前者有正负号选取,其符号由角的范围确定,必要时需要讨论,
后者没有符号选取,其结果的符号由sin α确定,应用十分方便.
作业布置
作业:教科书P158页,A组第6,7,8,10题,B组第4题.
目标检测
A.
C.
D.
B.
1
若sin(π-α)= 且α∈ ,则 等于( )
解析:由题意知sinα= ,α∈ ,
所以
所以
B
目标检测
A.
C.
D.
B.8
2
若f(x)=2tanx- ,则 的值是( )
解析:
又
故
B
目标检测
3
已知 ,540°<α<720°,则 =________.
解析:因为540°<α<720°,所以270°< <360°,
所以135°< <180°.
因为 ,所以
目标检测
4
已知sinφ= ,且φ是第三象限角,求下列各三角函数的值:
(1) ;(2)sin 2φ;(3) ;(4) .
解析:因为φ是第三象限角,所以cosφ=
(1)
(2)sin2φ=2sinφcosφ= .
目标检测
4
已知sin φ= ,且φ是第三象限角,求下列各三角函数的值:
(1) ;(2)sin 2φ;(3) ;(4) .
(3)因为φ是第三象限角,所以2kπ+π<φ<2kπ+ ,
所以 (k∈Z).
当k=2m时, (m∈Z),
当k=2m+1时, (m∈Z),
目标检测
4
已知sin φ= ,且φ是第三象限角,求下列各三角函数的值:
(1) ;(2)sin 2φ;(3) ;(4) .
(4)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
