2022-2023学年高一下学期数学北师大版(2019)必修第二册两角和与差的三角函数公式》第1课时课件(共23张PPT)
文档属性
| 名称 | 2022-2023学年高一下学期数学北师大版(2019)必修第二册两角和与差的三角函数公式》第1课时课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 827.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-07 06:22:37 | ||
图片预览








文档简介
(共23张PPT)
两角和与差的三角函数公式
第1课时
新知探究
问题1 如图,为世界著名的艺术殿堂——法国卢浮宫,它的正门入口处有一个金字塔建筑,它的设计者就是著名的美籍华人建筑师贝聿铭.
那么在测量这类建筑物的高度时(如右图),我们需要来解复合角∠DAC=α-β的正、余弦值,这就需要对两角差的正、余弦进行变换.
新知探究
问题2 如何用角α,β的正弦、余弦值来表示cos(α-β)呢?
有人认为cos(α-β)=cosα-cosβ,你认为正确吗?试举出两例加以说明.
不一定正确.
例如,当cosα-cosβ= 时,cos(α-β)≠cosα-cosβ.
再如,当 时,cos(α-β)= .
而cosα-cosβ= ,故cos(α-β)≠cosα-cosβ.
新知探究
问题3 计算下列各式子的值,并根据这些式子的共同特征,写出一个猜想.
猜想:cosαcosβ+sinαsinβ=cos(α-β).
①cos45°cos45°+sin45°sin45°=1;
③cos30°cos120°+sin30°sin120°=0.
②cos60°cos30°+sin60°sin30°= 60°cos30°+sin60°sin30°.
④cos150°cos210°+sin150°sin210°= .
新知探究
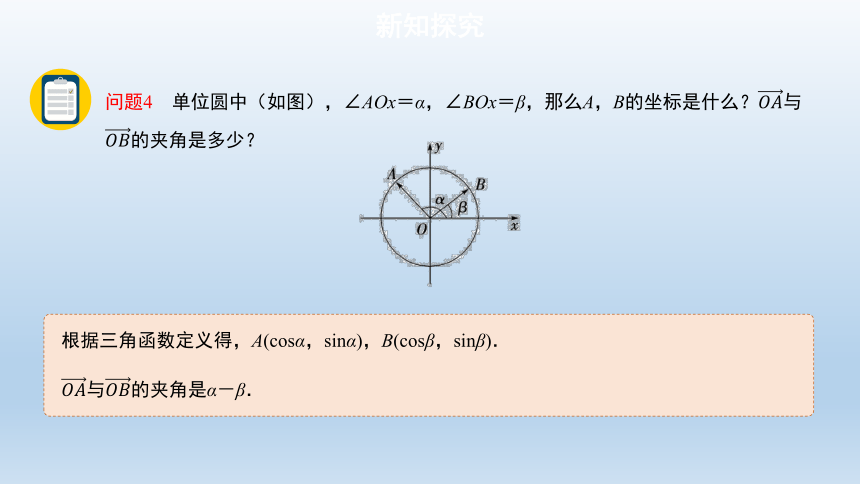
根据三角函数定义得,A(cosα,sinα),B(cosβ,sinβ).
与的夹角是α-β.
问题4 单位圆中(如图),∠AOx=α,∠BOx=β,那么A,B的坐标是什么?与的夹角是多少?
新知探究
追问1:根据上图,分别利用平面向量数量积的定义及坐标运算,求出的数量积各是什么?由此得出什么结论?
平面向量数量积定义:(α-β)=cos(α-β).
平面向量数量积坐标运算:=(cosα,sinα)·(cosβ,sinβ)=cosαcosβ+sinαsinβ.
根据数量积相等,得 cos(α-β)=cosαcosβ+sinαsinβ.
新知探究
两角差的余弦公式
cos(α-β)=cos αcos β+sin αsin β,记作Cα-β.
新知探究
追问2:公式Cα-β在结构上有什么特点?
①同名函数相乘:即两角余弦乘余弦,正弦乘正弦;
追问3:两角差的余弦公式的适用条件是什么?
公式中的α,β都是任意角,可以为常量,也可以为变角.
②将所得的积相加.
新知探究
问题5 把公式cos(α-β)=cosαcosβ+sinαsinβ中的β用-β代替,结果如何?
cos(α+β)=cos[(α-(-β)]
=cosαcos(-β)+sinαsin(-β)
=cosαcosβ-sinαsinβ.
新知探究
两角和的余弦公式
Cos(α+β)=cosαcosβ-sinαsinβ.记作Cα+β.
新知探究
追问1:你能根据余弦两角和差的公式的结构,总结它们的记忆口诀吗?
余余正正,符号相反.
追问2:如何利用两角差的余弦和两角和的余弦公式求cos15°?
因为15°=60°-45°,所以可用两角差的余弦公式求解.
例1 已知sinα+sinβ= ,cosα+cosβ= ,求cos(α-β)的值.
初步应用
由①+②得:1+1+2(sinαsinβ+cosαcosβ)=1,即2cos(α-β)=-1,
解析:由sinα+sinβ= 两边平方得:sin2α+sin2β+2sinαsinβ= ①
由cosα+cosβ= 两边平方得:cos2α+cos2β+2cosαcosβ= ②
所以cos(α-β)= .
初步应用
给条件求值问题要注意公式的正用、逆用,尤其是公式的逆用,要求能正确地找出所给式子与公式右边的异同,并积极创造条件逆用公式.
方法总结
例2 已知cosα= ,sin(α+β)= ,且α,β均为锐角,求β的值.
初步应用
解析: ∵α为锐角且cos α= ,
又α,β为锐角,
∴cosβ=cos[(α+β)-α]=cos(α+β)cos α+sin(α+β)sinα= .
∴sin α
又∵sin(α+β)= <sin α,
∴α+β∈(0,π).
∴α+β∈( ,).
∴cos(α+β)= .
又β为锐角,故β= .
初步应用
在解决此类题目时,一定要注意已知角与所求角之间的关系,恰当地运用拆角、拼角技巧,同时分析角之间的关系,利用角的代换化异角为同角.
方法总结
归纳小结
(1)已知某些角的三角函数值,求另外一些角的三角函数值时,要注意什么?
(2)给值求角的关键是什么?常用的角的变换技巧有哪些?
问题6 回归本节的学习,你有什么收获?可以从以下几个问题归纳.
(1)要注意观察已知角与所求表达式中角的关系,即拆角与凑角.
(2)关键是变角,把所求角用含已知角的式子表示;互余或互补关系的应用;
如 -α与 +α互余, +α与 π-α互补等.
作业布置
作业:教科书第152页,A组第1(1)(3)题,2(2),第3题.
1
目标检测
A
cos27°cos57°-sin27°cos147°等于( )
A.
C.
D.
B.
解析:原式=cos27°cos57°-sin27°cos(180°-33°)
=cos27°cos57°+sin27°cos33°
=cos(57°-27°)
=cos27°cos57°+sin27°sin57°
=cos30°
= .
2
目标检测
若角α,β均为锐角,sin α= ,cos(α+β)= ,则cos β=( )
A.
C.
D.
B.
解析: ∵α,β均为锐角, sin α= ,cos(α+β)= ,
∴
2
目标检测
A
若角α,β均为锐角,sinα= ,cos(α+β)= ,则cos β=( )
A.
C.
D.
B.
∴cosβ=cos[(α+β)-α]
=cos(α+β)cosα+sin(α+β)sinα
3
目标检测
已知α,β∈[0, ],sinα= ,cosβ= ,则cos(α+β)=________.
所以cosα= ,sinβ= ,
所以cos(α+β)=cosαcosβ-sinαsinβ=
解析:因为α,β∈[0, ],
4
目标检测
已知sinα ,β是第三象限角,求:
(1)cosα与sinβ的值.
(2)cos(α-β).
解析:(1)由于sinα= ,α∈
又由于cosβ= ,β是第三象限角,
故
故
4
目标检测
已知sin α ,β是第三象限角,求:
(1)cos α与sin β的值.
(2)cos(α-β).
(2)由(1)可得,
cos(α-β)=cos αcos β+sin αsin β
=右边.
故原等式成立.
两角和与差的三角函数公式
第1课时
新知探究
问题1 如图,为世界著名的艺术殿堂——法国卢浮宫,它的正门入口处有一个金字塔建筑,它的设计者就是著名的美籍华人建筑师贝聿铭.
那么在测量这类建筑物的高度时(如右图),我们需要来解复合角∠DAC=α-β的正、余弦值,这就需要对两角差的正、余弦进行变换.
新知探究
问题2 如何用角α,β的正弦、余弦值来表示cos(α-β)呢?
有人认为cos(α-β)=cosα-cosβ,你认为正确吗?试举出两例加以说明.
不一定正确.
例如,当cosα-cosβ= 时,cos(α-β)≠cosα-cosβ.
再如,当 时,cos(α-β)= .
而cosα-cosβ= ,故cos(α-β)≠cosα-cosβ.
新知探究
问题3 计算下列各式子的值,并根据这些式子的共同特征,写出一个猜想.
猜想:cosαcosβ+sinαsinβ=cos(α-β).
①cos45°cos45°+sin45°sin45°=1;
③cos30°cos120°+sin30°sin120°=0.
②cos60°cos30°+sin60°sin30°= 60°cos30°+sin60°sin30°.
④cos150°cos210°+sin150°sin210°= .
新知探究
根据三角函数定义得,A(cosα,sinα),B(cosβ,sinβ).
与的夹角是α-β.
问题4 单位圆中(如图),∠AOx=α,∠BOx=β,那么A,B的坐标是什么?与的夹角是多少?
新知探究
追问1:根据上图,分别利用平面向量数量积的定义及坐标运算,求出的数量积各是什么?由此得出什么结论?
平面向量数量积定义:(α-β)=cos(α-β).
平面向量数量积坐标运算:=(cosα,sinα)·(cosβ,sinβ)=cosαcosβ+sinαsinβ.
根据数量积相等,得 cos(α-β)=cosαcosβ+sinαsinβ.
新知探究
两角差的余弦公式
cos(α-β)=cos αcos β+sin αsin β,记作Cα-β.
新知探究
追问2:公式Cα-β在结构上有什么特点?
①同名函数相乘:即两角余弦乘余弦,正弦乘正弦;
追问3:两角差的余弦公式的适用条件是什么?
公式中的α,β都是任意角,可以为常量,也可以为变角.
②将所得的积相加.
新知探究
问题5 把公式cos(α-β)=cosαcosβ+sinαsinβ中的β用-β代替,结果如何?
cos(α+β)=cos[(α-(-β)]
=cosαcos(-β)+sinαsin(-β)
=cosαcosβ-sinαsinβ.
新知探究
两角和的余弦公式
Cos(α+β)=cosαcosβ-sinαsinβ.记作Cα+β.
新知探究
追问1:你能根据余弦两角和差的公式的结构,总结它们的记忆口诀吗?
余余正正,符号相反.
追问2:如何利用两角差的余弦和两角和的余弦公式求cos15°?
因为15°=60°-45°,所以可用两角差的余弦公式求解.
例1 已知sinα+sinβ= ,cosα+cosβ= ,求cos(α-β)的值.
初步应用
由①+②得:1+1+2(sinαsinβ+cosαcosβ)=1,即2cos(α-β)=-1,
解析:由sinα+sinβ= 两边平方得:sin2α+sin2β+2sinαsinβ= ①
由cosα+cosβ= 两边平方得:cos2α+cos2β+2cosαcosβ= ②
所以cos(α-β)= .
初步应用
给条件求值问题要注意公式的正用、逆用,尤其是公式的逆用,要求能正确地找出所给式子与公式右边的异同,并积极创造条件逆用公式.
方法总结
例2 已知cosα= ,sin(α+β)= ,且α,β均为锐角,求β的值.
初步应用
解析: ∵α为锐角且cos α= ,
又α,β为锐角,
∴cosβ=cos[(α+β)-α]=cos(α+β)cos α+sin(α+β)sinα= .
∴sin α
又∵sin(α+β)= <sin α,
∴α+β∈(0,π).
∴α+β∈( ,).
∴cos(α+β)= .
又β为锐角,故β= .
初步应用
在解决此类题目时,一定要注意已知角与所求角之间的关系,恰当地运用拆角、拼角技巧,同时分析角之间的关系,利用角的代换化异角为同角.
方法总结
归纳小结
(1)已知某些角的三角函数值,求另外一些角的三角函数值时,要注意什么?
(2)给值求角的关键是什么?常用的角的变换技巧有哪些?
问题6 回归本节的学习,你有什么收获?可以从以下几个问题归纳.
(1)要注意观察已知角与所求表达式中角的关系,即拆角与凑角.
(2)关键是变角,把所求角用含已知角的式子表示;互余或互补关系的应用;
如 -α与 +α互余, +α与 π-α互补等.
作业布置
作业:教科书第152页,A组第1(1)(3)题,2(2),第3题.
1
目标检测
A
cos27°cos57°-sin27°cos147°等于( )
A.
C.
D.
B.
解析:原式=cos27°cos57°-sin27°cos(180°-33°)
=cos27°cos57°+sin27°cos33°
=cos(57°-27°)
=cos27°cos57°+sin27°sin57°
=cos30°
= .
2
目标检测
若角α,β均为锐角,sin α= ,cos(α+β)= ,则cos β=( )
A.
C.
D.
B.
解析: ∵α,β均为锐角, sin α= ,cos(α+β)= ,
∴
2
目标检测
A
若角α,β均为锐角,sinα= ,cos(α+β)= ,则cos β=( )
A.
C.
D.
B.
∴cosβ=cos[(α+β)-α]
=cos(α+β)cosα+sin(α+β)sinα
3
目标检测
已知α,β∈[0, ],sinα= ,cosβ= ,则cos(α+β)=________.
所以cosα= ,sinβ= ,
所以cos(α+β)=cosαcosβ-sinαsinβ=
解析:因为α,β∈[0, ],
4
目标检测
已知sinα ,β是第三象限角,求:
(1)cosα与sinβ的值.
(2)cos(α-β).
解析:(1)由于sinα= ,α∈
又由于cosβ= ,β是第三象限角,
故
故
4
目标检测
已知sin α ,β是第三象限角,求:
(1)cos α与sin β的值.
(2)cos(α-β).
(2)由(1)可得,
cos(α-β)=cos αcos β+sin αsin β
=右边.
故原等式成立.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
