高中数学人教A版(2019)必修第二册分层练习6.1平面向量的概念B(含答案)
文档属性
| 名称 | 高中数学人教A版(2019)必修第二册分层练习6.1平面向量的概念B(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 561.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-07 07:47:55 | ||
图片预览




文档简介
一、单选题
1.设为单位向量,下列命题中:①若为平面内的某个向量,则;②若与平行,则;③若与平行且,则,假命题的个数是( )
A.0 B.1
C.2 D.3
2.给出下列命题:
①两个具有共同终点的向量,一定是共线向量;
②若是不共线的四点,则是四边形为平行四边形的充要条件;
③若与同向,且,则>;
④λ,μ为实数,若λ=μ,则与共线.
其中假命题的个数为( )
A.1 B.2
C.3 D.4
3.下列命题中,正确的是( )
A.若,,则
B.若,,则
C.若两个单位向量互相平行,则这两个单位向量相等
D.若,则与方向相同或相反
4.已知等边三角形中,是线段的中点,,垂足为是线段的中点,则
A. B.
C. D.
5.给出下列四个命题:①若,则;②若A,B,C,D是不共线的四点,则“”是“四边形ABCD为平行四边形”的充要条件;③若,,则;④的充要条件是且.其中正确命题的序号是( )
A.②③ B.①② C.③④ D.②④
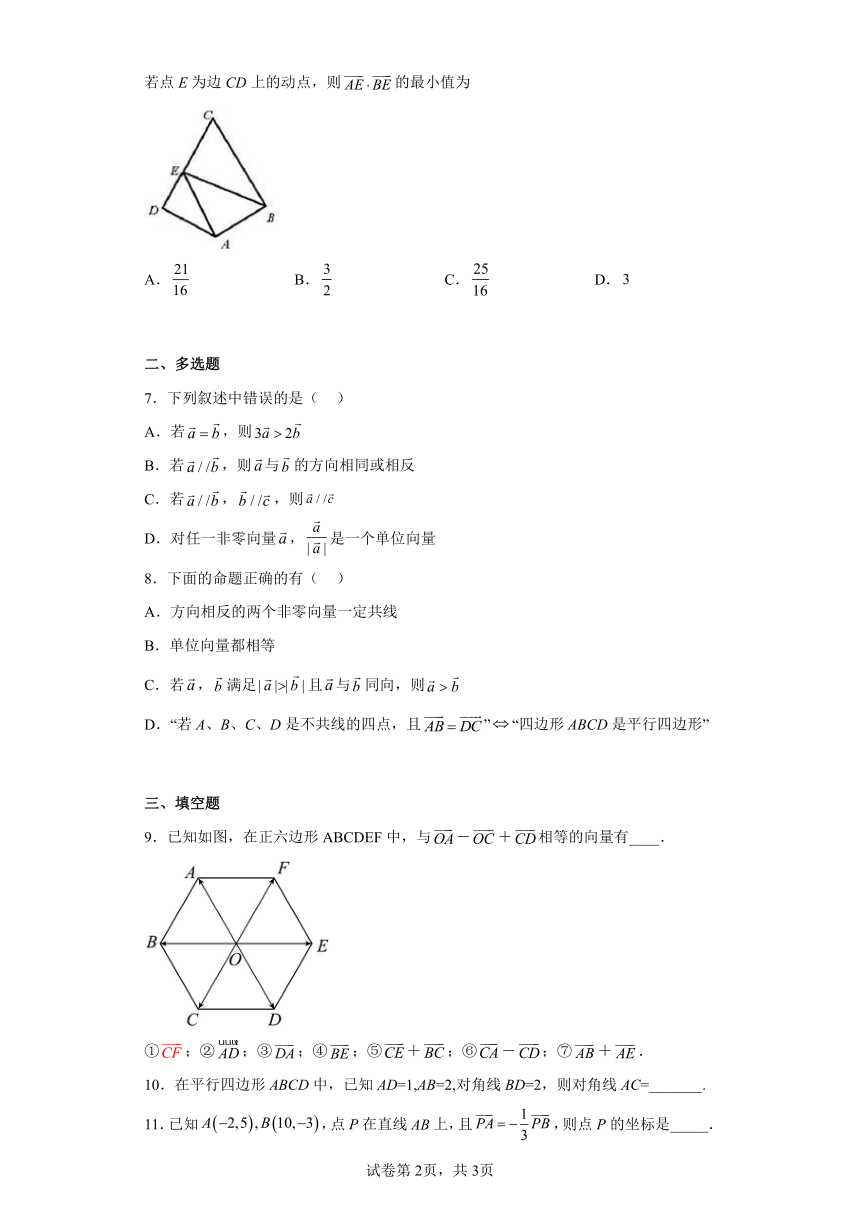
6.如图,在平面四边形ABCD中,
若点E为边CD上的动点,则的最小值为
A. B. C. D.
二、多选题
7.下列叙述中错误的是( )
A.若,则
B.若,则与的方向相同或相反
C.若,,则
D.对任一非零向量,是一个单位向量
8.下面的命题正确的有( )
A.方向相反的两个非零向量一定共线
B.单位向量都相等
C.若,满足且与同向,则
D.“若A、B、C、D是不共线的四点,且”“四边形ABCD是平行四边形”
三、填空题
9.已知如图,在正六边形ABCDEF中,与-+相等的向量有____.
①;②;③;④;⑤+;⑥-;⑦+.
10.在平行四边形ABCD中,已知AD=1,AB=2,对角线BD=2,则对角线AC=_______.
11.已知,点P在直线上,且,则点P的坐标是_____.
12.下列五个命题:
①向量与共线,则必在同一条直线上;
②如果向量与平行,则与方向相同或相反;
③四边形P1P2OA是平行四边形的充要条件是;
④若,则、的长度相等且方向相同或相反;
⑤由于零向量方向不确定,故零向量与任何向量不平行.
其中正确的命题有______个.
四、解答题
13.在中,已知,,.
(1)求的值;
(2)若,且,求在上的投影的取值范围.
14.已知向量,.
(1)若,求的值;
(2)若,,求的值.
15.已知飞机从甲地按北偏东30°的方向飞行2000km到达乙地,再从乙地按南偏东30°的方向飞行2000km到达丙地,再从丙地按西南方向飞行1000km到达丁地,问丁地在甲地的什么方向?丁地距甲地多远?
16.如图,矩形ACDF中,AC=2CD,B,E分别为AC,DF的中点,写出:
(1)与相等的向量;
(2)与的负向量相等的向量;
(3)与共线的向量.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】由向量是既有大小又有方向的量,两个非零向量平行的方向有两种情况:一是同向,二是反向,可判断
【详解】向量是既有大小又有方向的量,与的模相同,但方向不一定相同,故①是假命题;若与平行,则与的方向有两种情况:一是同向,二是反向,反向时,故②③也是假命题.
综上所述,假命题的个数是3.
故选:D
2.C
【分析】根据向量共线定义判断①;根据向量相等的定义和平行四边形的定义判断②;根据两向量不能比较大小判断③;举反例否定④.
【详解】①不正确.当起点不在同一直线上时,虽然终点相同,但向量不共线;
②正确.∵=,∴||=||且;
又∵是不共线的四点,∴四边形是平行四边形.
反之,若四边形是平行四边形,
则且与方向相同,因此=;
③不正确.两向量不能比较大小.
④不正确.当时,与可以为任意向量,
满足λ=μ,但与不一定共线.
故选:.
3.B
【分析】对ABC选项找出反例,证明其错误,选项B根据传递性很明显正确,即可求解.
【详解】对于A选项: 平行于任何向量,若,满足,,但不一定满足,故A错;
对于B选项:根据向量传递性,正确;
对于C选项:两个单位向量互相平行,这两个单位向量相等或相反(大小相等,方向完全相反),故C错;
对于D选项:零向量与任何非零向量都平行,且零向量的方向任意.如果中有一个是零向量,那么方向相同或相反,或者不同,故D错.
故选:B.
4.C
【分析】先由中线向量定理得到=,=,再将,,都用基底表示,利用向量相等,求得关系.
【详解】∵是线段的中点,∴==;
∵是线段的中点,∴=;
又=;
令,
则-=(,
∴,,解得,,∴,
故选C.
【点睛】本题考查了平面向量基本定理的应用,考查了中线向量定理、向量相等的概念及应用,属于中档题.
5.A
【分析】对于①,根据向量相等的概念分析可知不正确;对于②,根据向量相等的概念以及充要条件的概念分析可知正确;对于③,根据向量相等的概念分析可知正确;对于④,根据向量相等的概念以及充要条件的概念分析可知不正确.
【详解】对于①,两个向量的长度相等,不能推出两个向量的方向的关系,故①错误;
对于②,因为A,B,C,D是不共线的四点,且 等价于且,即等价于四边形ABCD为平行四边形,故②正确;
对于③,若,,则;显然正确,故③正确;
对于④,由可以推出且,但是由且可能推出,故“且”是“”的必要不充分条件,故④不正确,
故选:A
【点睛】关键点点睛:掌握向量相等的概念和充要条件的概念是解题关键.
6.A
【详解】分析:由题意可得为等腰三角形,为等边三角形,把数量积分拆,设,数量积转化为关于t的函数,用函数可求得最小值。
详解:连接BD,取AD中点为O,可知为等腰三角形,而,所以为等边三角形,。设
=
所以当时,上式取最小值 ,选A.
点睛:本题考查的是平面向量基本定理与向量的拆分,需要选择合适的基底,再把其它向量都用基底表示。同时利用向量共线转化为函数求最值。
7.ABC
【分析】根据向量不能比较大小可判断A;根据共线向量的定义可判断B;当时可判断C;根据单位向量的定义可判断D,进而可得答案.
【详解】对于A,因为向量是既有大小又有方向的量,所以向量不能比较大小,故A错误;
对于B,零向量与任意向量平行,且零向量的方向是任意的,所以若,
则对于非零向量,必有,但与的方向不一定相同或相反,故B错误;
对于C,若,则零向量与任意向量平行,
所以对任意向量与,均有,,故此时与不一定平行,故C错误;
对于D,由单位向量的定义可得,对任一非零向量,其单位向量为,故D正确.
故选:ABC.
8.AD
【分析】根据向量的定义和性质,逐项判断正误即可.
【详解】对于A,由相反向量的概念可知A正确;
对于B,任意两个单位向量的模相等,其方向未必相同,故B错误;
对于C,向量之间不能比较大小,只能比较向量的模,故C错误;
对于D,若A、B、C、D是不共线的四点,且,
可得,且,故四边形ABCD是平行四边形;
若四边形ABCD是平行四边形,可知,且,
此时A、B、C、D是不共线的四点,且,故D正确.
故选:AD.
9.①
【分析】直接利用平面向量加法与减法的运算法则以及相等向量的定义逐一判断即可.
【详解】化简,①合题意;
由正六边形的性质,结合图可得向量、、与向量方向不同,
根据向量相等的定义可得向量、、与向量不相等,
②③④不合题意;
因为++ ,⑤不合题意;
-,⑥不合题意;
,⑦不合题意,故答案为①.
【点睛】本题主要考查平面向量加法与减法的运算法则以及相等向量的定义,属于基础题. 相等向量的定义:长度相等且方向相同的向量叫相等向量;两个向量只有当他们的模相等且方向相同时,才能称它们相等.
10.
【详解】在中, AD=1,AB=2,对角线BD=2,由余弦定理可得, ,在中, ,
故对角线AC=,应填.
11.
【分析】由题意可知,三点共线,且有,设出点的坐标,利用向量相等的条件建立方程求出点P的坐标
【详解】解:设
,点P在直线上
,
,则有
解得
【点睛】本题考查向量共线的坐标表示,向量相等的条件.解题的关键是由题设条件得出两向量的数乘关系,再利用向量相等的条件得出坐标的方程求出P的坐标.
12.0
【分析】利用向量共线可判断①②③;利用相等向量可判断④;利用零向量与任何向量共线可判断⑤.
【详解】对于①,向量与共线,则直线与直线可能平行,故①错;
对于②,若为零向量,零向量与任意向量平行,故②错;
对于③,,则四点可能共线,故③错;
对于④,,只能说明、的长度相等但确定不了方向,故④错;
对于⑤,零向量与任何向量平行,故⑤错.
所以正确的命题有0个,
故答案为:0
13.(1)1,(2)
【分析】(1)由,两边平方化简可求得的值;
(2)先表示出,,从而可得在上的投影为,然后由的不同取值范围求其值可得结果.
【详解】解:(1)因为,所以,
,
因为 ,,
所以,即
,所以,
(2)因为,且,
所以,
因为,,,,
所以,
由,得
,
所以在上的投影为,
当时,,
因为,所以,所以,
时,
当且 时,
时,, 所以,
时,,所以 ,
综上,在上的投影的取值范围为.
【点睛】此题考查向量的模,向量上的投影,考查了分类讨论思想,考查了计算能力,属于中档题.
14.(1);(2)或
【分析】(1)由共线定理结合齐次式弦化切可求;
(2)由数量积运算性质结合三角函数的恒等变换得,再结合三角函数的性质可得到结果.
【详解】解:(1),,,
,,
(2),,
,
,
,
,,
或,
或.
【点睛】本题考查了平面向量的共线定理、数量积运算性质、三角函数的性质,考查了推理能力与计算能力,属于中档题.
15.丁地在甲地的东南方向,距甲地1000km.
【详解】如图所示,A、B、C、D分别表示甲地、乙地、丙地、丁地,依题意知,三角形ABC为正三角形,
∴AC=2000km.
又∵∠ACD=45°,CD=1000,∴△ACD为直角三角形,
即AD=1000km,∠CAD=45°.
故丁地在甲地的东南方向,距甲地1000km.
16.(1),;(2),,;(3),,,,
【分析】(1)利用相等的向量的定义即可得出;(2)的负向量为,再利用相等的向量的定义即可得出;(3)利用共线的向量的定义即可得出.
【详解】在矩形ACDF中,且AC=2CD,B,E分别为AC,DF的中点,得
(1)与相等的向量为:,;
(2)与的负向量相等的向量为:,,;
(3)与共线的向量为:,,,,.
【点睛】本题考查了相等向量,共线向量、负向量的定义,考查了推理能力与计算能力,属于基础题.
答案第1页,共2页
答案第1页,共2页
1.设为单位向量,下列命题中:①若为平面内的某个向量,则;②若与平行,则;③若与平行且,则,假命题的个数是( )
A.0 B.1
C.2 D.3
2.给出下列命题:
①两个具有共同终点的向量,一定是共线向量;
②若是不共线的四点,则是四边形为平行四边形的充要条件;
③若与同向,且,则>;
④λ,μ为实数,若λ=μ,则与共线.
其中假命题的个数为( )
A.1 B.2
C.3 D.4
3.下列命题中,正确的是( )
A.若,,则
B.若,,则
C.若两个单位向量互相平行,则这两个单位向量相等
D.若,则与方向相同或相反
4.已知等边三角形中,是线段的中点,,垂足为是线段的中点,则
A. B.
C. D.
5.给出下列四个命题:①若,则;②若A,B,C,D是不共线的四点,则“”是“四边形ABCD为平行四边形”的充要条件;③若,,则;④的充要条件是且.其中正确命题的序号是( )
A.②③ B.①② C.③④ D.②④
6.如图,在平面四边形ABCD中,
若点E为边CD上的动点,则的最小值为
A. B. C. D.
二、多选题
7.下列叙述中错误的是( )
A.若,则
B.若,则与的方向相同或相反
C.若,,则
D.对任一非零向量,是一个单位向量
8.下面的命题正确的有( )
A.方向相反的两个非零向量一定共线
B.单位向量都相等
C.若,满足且与同向,则
D.“若A、B、C、D是不共线的四点,且”“四边形ABCD是平行四边形”
三、填空题
9.已知如图,在正六边形ABCDEF中,与-+相等的向量有____.
①;②;③;④;⑤+;⑥-;⑦+.
10.在平行四边形ABCD中,已知AD=1,AB=2,对角线BD=2,则对角线AC=_______.
11.已知,点P在直线上,且,则点P的坐标是_____.
12.下列五个命题:
①向量与共线,则必在同一条直线上;
②如果向量与平行,则与方向相同或相反;
③四边形P1P2OA是平行四边形的充要条件是;
④若,则、的长度相等且方向相同或相反;
⑤由于零向量方向不确定,故零向量与任何向量不平行.
其中正确的命题有______个.
四、解答题
13.在中,已知,,.
(1)求的值;
(2)若,且,求在上的投影的取值范围.
14.已知向量,.
(1)若,求的值;
(2)若,,求的值.
15.已知飞机从甲地按北偏东30°的方向飞行2000km到达乙地,再从乙地按南偏东30°的方向飞行2000km到达丙地,再从丙地按西南方向飞行1000km到达丁地,问丁地在甲地的什么方向?丁地距甲地多远?
16.如图,矩形ACDF中,AC=2CD,B,E分别为AC,DF的中点,写出:
(1)与相等的向量;
(2)与的负向量相等的向量;
(3)与共线的向量.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】由向量是既有大小又有方向的量,两个非零向量平行的方向有两种情况:一是同向,二是反向,可判断
【详解】向量是既有大小又有方向的量,与的模相同,但方向不一定相同,故①是假命题;若与平行,则与的方向有两种情况:一是同向,二是反向,反向时,故②③也是假命题.
综上所述,假命题的个数是3.
故选:D
2.C
【分析】根据向量共线定义判断①;根据向量相等的定义和平行四边形的定义判断②;根据两向量不能比较大小判断③;举反例否定④.
【详解】①不正确.当起点不在同一直线上时,虽然终点相同,但向量不共线;
②正确.∵=,∴||=||且;
又∵是不共线的四点,∴四边形是平行四边形.
反之,若四边形是平行四边形,
则且与方向相同,因此=;
③不正确.两向量不能比较大小.
④不正确.当时,与可以为任意向量,
满足λ=μ,但与不一定共线.
故选:.
3.B
【分析】对ABC选项找出反例,证明其错误,选项B根据传递性很明显正确,即可求解.
【详解】对于A选项: 平行于任何向量,若,满足,,但不一定满足,故A错;
对于B选项:根据向量传递性,正确;
对于C选项:两个单位向量互相平行,这两个单位向量相等或相反(大小相等,方向完全相反),故C错;
对于D选项:零向量与任何非零向量都平行,且零向量的方向任意.如果中有一个是零向量,那么方向相同或相反,或者不同,故D错.
故选:B.
4.C
【分析】先由中线向量定理得到=,=,再将,,都用基底表示,利用向量相等,求得关系.
【详解】∵是线段的中点,∴==;
∵是线段的中点,∴=;
又=;
令,
则-=(,
∴,,解得,,∴,
故选C.
【点睛】本题考查了平面向量基本定理的应用,考查了中线向量定理、向量相等的概念及应用,属于中档题.
5.A
【分析】对于①,根据向量相等的概念分析可知不正确;对于②,根据向量相等的概念以及充要条件的概念分析可知正确;对于③,根据向量相等的概念分析可知正确;对于④,根据向量相等的概念以及充要条件的概念分析可知不正确.
【详解】对于①,两个向量的长度相等,不能推出两个向量的方向的关系,故①错误;
对于②,因为A,B,C,D是不共线的四点,且 等价于且,即等价于四边形ABCD为平行四边形,故②正确;
对于③,若,,则;显然正确,故③正确;
对于④,由可以推出且,但是由且可能推出,故“且”是“”的必要不充分条件,故④不正确,
故选:A
【点睛】关键点点睛:掌握向量相等的概念和充要条件的概念是解题关键.
6.A
【详解】分析:由题意可得为等腰三角形,为等边三角形,把数量积分拆,设,数量积转化为关于t的函数,用函数可求得最小值。
详解:连接BD,取AD中点为O,可知为等腰三角形,而,所以为等边三角形,。设
=
所以当时,上式取最小值 ,选A.
点睛:本题考查的是平面向量基本定理与向量的拆分,需要选择合适的基底,再把其它向量都用基底表示。同时利用向量共线转化为函数求最值。
7.ABC
【分析】根据向量不能比较大小可判断A;根据共线向量的定义可判断B;当时可判断C;根据单位向量的定义可判断D,进而可得答案.
【详解】对于A,因为向量是既有大小又有方向的量,所以向量不能比较大小,故A错误;
对于B,零向量与任意向量平行,且零向量的方向是任意的,所以若,
则对于非零向量,必有,但与的方向不一定相同或相反,故B错误;
对于C,若,则零向量与任意向量平行,
所以对任意向量与,均有,,故此时与不一定平行,故C错误;
对于D,由单位向量的定义可得,对任一非零向量,其单位向量为,故D正确.
故选:ABC.
8.AD
【分析】根据向量的定义和性质,逐项判断正误即可.
【详解】对于A,由相反向量的概念可知A正确;
对于B,任意两个单位向量的模相等,其方向未必相同,故B错误;
对于C,向量之间不能比较大小,只能比较向量的模,故C错误;
对于D,若A、B、C、D是不共线的四点,且,
可得,且,故四边形ABCD是平行四边形;
若四边形ABCD是平行四边形,可知,且,
此时A、B、C、D是不共线的四点,且,故D正确.
故选:AD.
9.①
【分析】直接利用平面向量加法与减法的运算法则以及相等向量的定义逐一判断即可.
【详解】化简,①合题意;
由正六边形的性质,结合图可得向量、、与向量方向不同,
根据向量相等的定义可得向量、、与向量不相等,
②③④不合题意;
因为++ ,⑤不合题意;
-,⑥不合题意;
,⑦不合题意,故答案为①.
【点睛】本题主要考查平面向量加法与减法的运算法则以及相等向量的定义,属于基础题. 相等向量的定义:长度相等且方向相同的向量叫相等向量;两个向量只有当他们的模相等且方向相同时,才能称它们相等.
10.
【详解】在中, AD=1,AB=2,对角线BD=2,由余弦定理可得, ,在中, ,
故对角线AC=,应填.
11.
【分析】由题意可知,三点共线,且有,设出点的坐标,利用向量相等的条件建立方程求出点P的坐标
【详解】解:设
,点P在直线上
,
,则有
解得
【点睛】本题考查向量共线的坐标表示,向量相等的条件.解题的关键是由题设条件得出两向量的数乘关系,再利用向量相等的条件得出坐标的方程求出P的坐标.
12.0
【分析】利用向量共线可判断①②③;利用相等向量可判断④;利用零向量与任何向量共线可判断⑤.
【详解】对于①,向量与共线,则直线与直线可能平行,故①错;
对于②,若为零向量,零向量与任意向量平行,故②错;
对于③,,则四点可能共线,故③错;
对于④,,只能说明、的长度相等但确定不了方向,故④错;
对于⑤,零向量与任何向量平行,故⑤错.
所以正确的命题有0个,
故答案为:0
13.(1)1,(2)
【分析】(1)由,两边平方化简可求得的值;
(2)先表示出,,从而可得在上的投影为,然后由的不同取值范围求其值可得结果.
【详解】解:(1)因为,所以,
,
因为 ,,
所以,即
,所以,
(2)因为,且,
所以,
因为,,,,
所以,
由,得
,
所以在上的投影为,
当时,,
因为,所以,所以,
时,
当且 时,
时,, 所以,
时,,所以 ,
综上,在上的投影的取值范围为.
【点睛】此题考查向量的模,向量上的投影,考查了分类讨论思想,考查了计算能力,属于中档题.
14.(1);(2)或
【分析】(1)由共线定理结合齐次式弦化切可求;
(2)由数量积运算性质结合三角函数的恒等变换得,再结合三角函数的性质可得到结果.
【详解】解:(1),,,
,,
(2),,
,
,
,
,,
或,
或.
【点睛】本题考查了平面向量的共线定理、数量积运算性质、三角函数的性质,考查了推理能力与计算能力,属于中档题.
15.丁地在甲地的东南方向,距甲地1000km.
【详解】如图所示,A、B、C、D分别表示甲地、乙地、丙地、丁地,依题意知,三角形ABC为正三角形,
∴AC=2000km.
又∵∠ACD=45°,CD=1000,∴△ACD为直角三角形,
即AD=1000km,∠CAD=45°.
故丁地在甲地的东南方向,距甲地1000km.
16.(1),;(2),,;(3),,,,
【分析】(1)利用相等的向量的定义即可得出;(2)的负向量为,再利用相等的向量的定义即可得出;(3)利用共线的向量的定义即可得出.
【详解】在矩形ACDF中,且AC=2CD,B,E分别为AC,DF的中点,得
(1)与相等的向量为:,;
(2)与的负向量相等的向量为:,,;
(3)与共线的向量为:,,,,.
【点睛】本题考查了相等向量,共线向量、负向量的定义,考查了推理能力与计算能力,属于基础题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
