3.9 求不规则物体的体积(教学课件)-五年级数学下册人教版(共28张PPT)
文档属性
| 名称 | 3.9 求不规则物体的体积(教学课件)-五年级数学下册人教版(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-07 14:42:58 | ||
图片预览






文档简介
(共28张PPT)
小学数学·五年级(下)·RJ
第9课时 求不规则物体
的体积
经历探究测量不规则物体体积方法的过程,体验“等积变形”的转化过程,获得综合运用所学知识测量不规则物体体积的活动经验和具体方法。
进一步熟悉长方体和正方体容积计算方法,掌握用“排水法”求不规则物体的体积。
培养学生的独立思考、严肃认真的学习态度,提高学生综合学习能力。
在测量不规则物体体积的过程中感悟转化的数学思想。
综合运用所学知识测量不规则物体体积的活动经验和具体方法。
在动手操作中初步建立“转化”的数学思想。
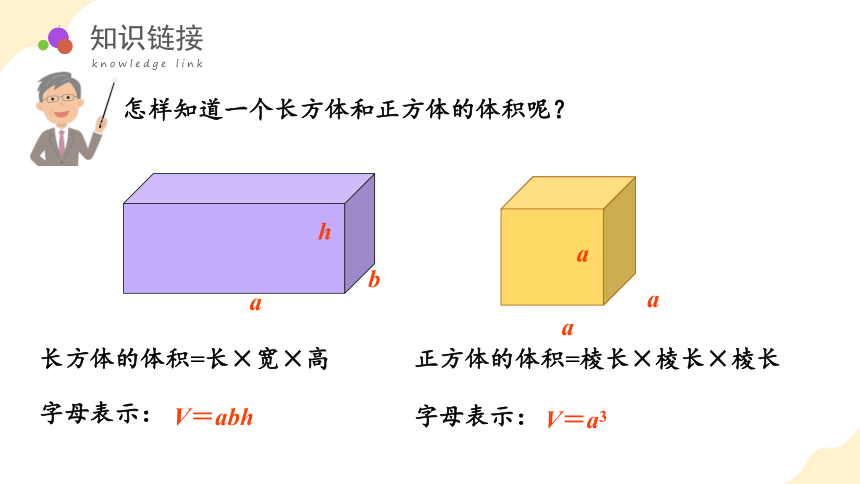
怎样知道一个长方体和正方体的体积呢?
a
b
h
a
a
a
长方体的体积=长×宽×高
字母表示:
V=abh
正方体的体积=棱长×棱长×棱长
字母表示:
V=a3
这些物体的形状不规则,不能用公式计算,那该怎样求它们的体积呢?
橡皮泥
土豆
梨
石块
观察下面物体的形状,用已有的体积公式可以计算它们的体积吗?
探究用等体积变形的方法测量不规则物体的体积
阅读与理解
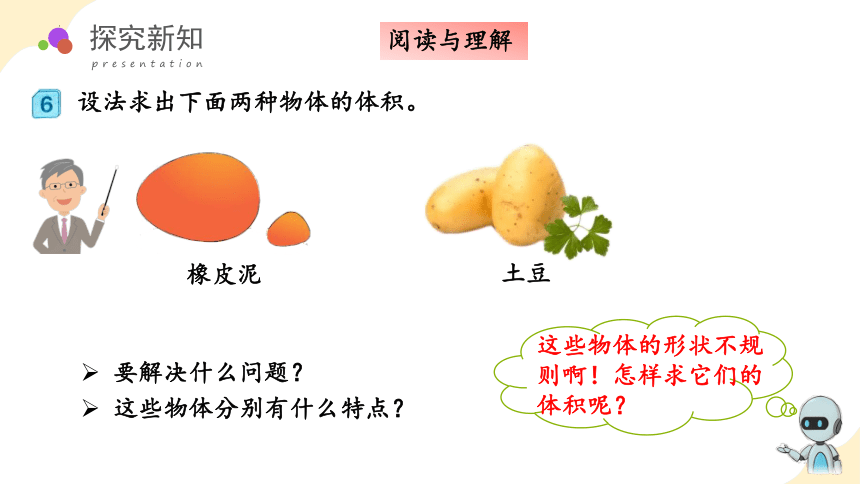
这些物体的形状不规则啊!怎样求它们的体积呢?
设法求出下面两种物体的体积。
橡皮泥
土豆
要解决什么问题?
这些物体分别有什么特点?
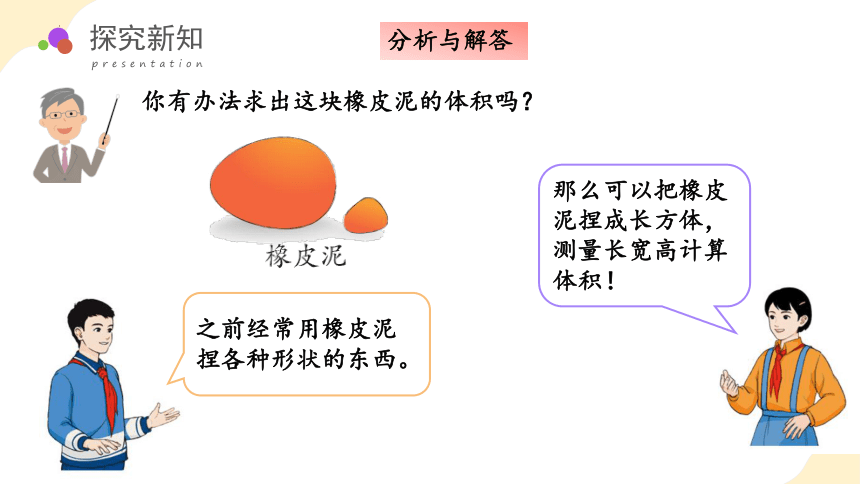
你有办法求出这块橡皮泥的体积吗?
分析与解答
之前经常用橡皮泥捏各种形状的东西。
那么可以把橡皮泥捏成长方体,测量长宽高计算体积!
你有办法求出这块橡皮泥的体积吗?
橡皮泥柔软,可以捏成各种立体图形。
形状变了,体积不变
等积形变
不规则物体
不改变原有物体体积
转化
规则物体
分析与解答
探究用排水法测量不规则物体的体积
可以在乌鸦喝水的故事中收到启发,用排水法试一试。
设法求出下面土豆的体积。
土豆
不能改变形状的土豆怎么办呢?
分析与解答
试一试,测量土豆的体积。
实验
土豆
量杯
操
作
要
求
1. 先小组讨论测量的方案,再动手实验。
2. 活动过程中,小组成员要分工合作:1人发言,2人 操作,2人记录,1人观察。
3. 活动过程中,注意保持教室的干净整洁。
分析与解答
试一试,测量土豆的体积。
实验
土豆
量杯
求不规则物体的体积(实验记录)
1.所测量物体名称 2.我们选择的测量工具
3.我们的测量方法 4.我们的发现
分析与解答
试一试,测量土豆的体积。
放入前水的体积是( )ml
放入后的体积变为( )ml
250
400
水为什么会升高?
因为土豆进去占据了一部分空间。
右面水杯中的400毫升是土豆和水的体积和。
分析与解答
试一试,测量土豆的体积。
250 ml
400 ml
① V水=250
②V水 + V土豆=400
V土豆=400 – 250=150ml
上升的水的体积=土豆的体积
分析与解答
试一试,测量土豆的体积。
上升的水的体积=梨的体积
不规则物体体积=水面上升后的体积 水面上升前的体积
注意:不规则物体必须完全浸没在水中。
回顾与反思
1.用排水法求不规则物体的体积需要记录哪些数据?
(1)开始时水的体积;
(2)放入不规则物体后的总体积;
2.可以利用上面的方法测量乒乓球、冰块的体积吗?为什么?
不能。因为兵乓球没有沉入水中,而冰块又与水融合在一起了。
回顾与反思
达标练习,巩固成果
1.下图中珊瑚石的体积是多少?
方法一: 8×8× 7- 8×8× 6 =64(cm3)
不规则物体的体积=容器的底面积×水面上升的高度
不规则物体的体积=水和不规则物体的总体积 水的体积
方法二: 8×8×( 7-6 )=64(cm3)
2.将一块假山石放在一个盛有水的,底面积为51dm2的长方体鱼缸中,完全浸没后,水面上升了3cm。这块假山石的体积是多大?
V=Sh
=51×0.3
=15.3(立方分米)
答:这块铁块的体积是5立方厘米。
上升部分水的体积=假山石的体积
3cm=0.3dm
3.将一些水倒入一个长6分米、宽3分米、高4分米的长方体玻璃容器中,此时水深2分米,把一个石块放入水中,完全浸没后,水深变为3分米。求这个石块的体积。
计算中属于多余条件,但是能帮我们确认放入石块后水没有溢出。
6×3×(3-2)=18(立方分米)
答:这个石块的体积是18立方分米。
4. 在一个长 8 m、宽 5 m、高 2 m 的水池中注满水,然后把两条长 3 m、宽 2 m、高 4 m 的石柱立着放入池中,水池溢出的水的体积是多少?
3×2×2×2=24(m3)
答:水池溢出的水的体积是 24 m3。
5.有一只长50厘米,宽40厘米的长方体玻璃水缸中,放入一块棱长2分米的正方体铁块后,水面会上升多少厘米?
V=a3
=20×20×20=8000(立方厘米)
答:水面会上升4厘米。
2分米=20厘米
8000÷(50×40)=4(厘米)
6. 求下图中大圆球的体积。
24 mL=24 cm3,12 mL=12 cm3 (24-12) ÷ 3=4(cm3)
12 – 4 = 8(cm3)
小球:
大球:
古希腊国王艾希罗交给金匠一块黄金,让他做一顶王冠,王冠做成后,国王拿在手里觉得有点轻。他怀疑金匠掺了假,可是金匠以脑袋担保说没有,并当面拿来秤来称。 结果与原来的金块一样重。国王还是有些怀疑,可他又拿不出证据,于是把阿基米德叫来,要他来解决这个难题。
阿基米德苦思冥想,把所有想到的办法,都作了尝试,然而仍不能揭开王冠的秘密。 在一次泡澡的时候,阿基米德忽然翻身跃起,想到了办法。
原来,阿基米德由澡盆溢水找到了解决王冠问题的方法:相同质量的相同物质泡在水里,溢出的水的体积应该相同,如果把王冠放到水里,溢出的水的体积应该与相同质量的金块的体积相同,否则王冠里肯定掺有假。
同学们,这节课你有哪些收获?
不规则物体
规则物体
转化
捏压——转化成长方体或正方体
排水法:
上升的那部分水的体积=不规则物体的体积。(不溶于水、不漂浮的物体)
注意:物体一定要完全浸没在水中。
★ 完成《分层作业》;
★★ 实验活动,可以选择合适的容器,测量数据,测量生活中一些不规则物体的体积。
小学数学·五年级(下)·RJ
第9课时 求不规则物体
的体积
经历探究测量不规则物体体积方法的过程,体验“等积变形”的转化过程,获得综合运用所学知识测量不规则物体体积的活动经验和具体方法。
进一步熟悉长方体和正方体容积计算方法,掌握用“排水法”求不规则物体的体积。
培养学生的独立思考、严肃认真的学习态度,提高学生综合学习能力。
在测量不规则物体体积的过程中感悟转化的数学思想。
综合运用所学知识测量不规则物体体积的活动经验和具体方法。
在动手操作中初步建立“转化”的数学思想。
怎样知道一个长方体和正方体的体积呢?
a
b
h
a
a
a
长方体的体积=长×宽×高
字母表示:
V=abh
正方体的体积=棱长×棱长×棱长
字母表示:
V=a3
这些物体的形状不规则,不能用公式计算,那该怎样求它们的体积呢?
橡皮泥
土豆
梨
石块
观察下面物体的形状,用已有的体积公式可以计算它们的体积吗?
探究用等体积变形的方法测量不规则物体的体积
阅读与理解
这些物体的形状不规则啊!怎样求它们的体积呢?
设法求出下面两种物体的体积。
橡皮泥
土豆
要解决什么问题?
这些物体分别有什么特点?
你有办法求出这块橡皮泥的体积吗?
分析与解答
之前经常用橡皮泥捏各种形状的东西。
那么可以把橡皮泥捏成长方体,测量长宽高计算体积!
你有办法求出这块橡皮泥的体积吗?
橡皮泥柔软,可以捏成各种立体图形。
形状变了,体积不变
等积形变
不规则物体
不改变原有物体体积
转化
规则物体
分析与解答
探究用排水法测量不规则物体的体积
可以在乌鸦喝水的故事中收到启发,用排水法试一试。
设法求出下面土豆的体积。
土豆
不能改变形状的土豆怎么办呢?
分析与解答
试一试,测量土豆的体积。
实验
土豆
量杯
操
作
要
求
1. 先小组讨论测量的方案,再动手实验。
2. 活动过程中,小组成员要分工合作:1人发言,2人 操作,2人记录,1人观察。
3. 活动过程中,注意保持教室的干净整洁。
分析与解答
试一试,测量土豆的体积。
实验
土豆
量杯
求不规则物体的体积(实验记录)
1.所测量物体名称 2.我们选择的测量工具
3.我们的测量方法 4.我们的发现
分析与解答
试一试,测量土豆的体积。
放入前水的体积是( )ml
放入后的体积变为( )ml
250
400
水为什么会升高?
因为土豆进去占据了一部分空间。
右面水杯中的400毫升是土豆和水的体积和。
分析与解答
试一试,测量土豆的体积。
250 ml
400 ml
① V水=250
②V水 + V土豆=400
V土豆=400 – 250=150ml
上升的水的体积=土豆的体积
分析与解答
试一试,测量土豆的体积。
上升的水的体积=梨的体积
不规则物体体积=水面上升后的体积 水面上升前的体积
注意:不规则物体必须完全浸没在水中。
回顾与反思
1.用排水法求不规则物体的体积需要记录哪些数据?
(1)开始时水的体积;
(2)放入不规则物体后的总体积;
2.可以利用上面的方法测量乒乓球、冰块的体积吗?为什么?
不能。因为兵乓球没有沉入水中,而冰块又与水融合在一起了。
回顾与反思
达标练习,巩固成果
1.下图中珊瑚石的体积是多少?
方法一: 8×8× 7- 8×8× 6 =64(cm3)
不规则物体的体积=容器的底面积×水面上升的高度
不规则物体的体积=水和不规则物体的总体积 水的体积
方法二: 8×8×( 7-6 )=64(cm3)
2.将一块假山石放在一个盛有水的,底面积为51dm2的长方体鱼缸中,完全浸没后,水面上升了3cm。这块假山石的体积是多大?
V=Sh
=51×0.3
=15.3(立方分米)
答:这块铁块的体积是5立方厘米。
上升部分水的体积=假山石的体积
3cm=0.3dm
3.将一些水倒入一个长6分米、宽3分米、高4分米的长方体玻璃容器中,此时水深2分米,把一个石块放入水中,完全浸没后,水深变为3分米。求这个石块的体积。
计算中属于多余条件,但是能帮我们确认放入石块后水没有溢出。
6×3×(3-2)=18(立方分米)
答:这个石块的体积是18立方分米。
4. 在一个长 8 m、宽 5 m、高 2 m 的水池中注满水,然后把两条长 3 m、宽 2 m、高 4 m 的石柱立着放入池中,水池溢出的水的体积是多少?
3×2×2×2=24(m3)
答:水池溢出的水的体积是 24 m3。
5.有一只长50厘米,宽40厘米的长方体玻璃水缸中,放入一块棱长2分米的正方体铁块后,水面会上升多少厘米?
V=a3
=20×20×20=8000(立方厘米)
答:水面会上升4厘米。
2分米=20厘米
8000÷(50×40)=4(厘米)
6. 求下图中大圆球的体积。
24 mL=24 cm3,12 mL=12 cm3 (24-12) ÷ 3=4(cm3)
12 – 4 = 8(cm3)
小球:
大球:
古希腊国王艾希罗交给金匠一块黄金,让他做一顶王冠,王冠做成后,国王拿在手里觉得有点轻。他怀疑金匠掺了假,可是金匠以脑袋担保说没有,并当面拿来秤来称。 结果与原来的金块一样重。国王还是有些怀疑,可他又拿不出证据,于是把阿基米德叫来,要他来解决这个难题。
阿基米德苦思冥想,把所有想到的办法,都作了尝试,然而仍不能揭开王冠的秘密。 在一次泡澡的时候,阿基米德忽然翻身跃起,想到了办法。
原来,阿基米德由澡盆溢水找到了解决王冠问题的方法:相同质量的相同物质泡在水里,溢出的水的体积应该相同,如果把王冠放到水里,溢出的水的体积应该与相同质量的金块的体积相同,否则王冠里肯定掺有假。
同学们,这节课你有哪些收获?
不规则物体
规则物体
转化
捏压——转化成长方体或正方体
排水法:
上升的那部分水的体积=不规则物体的体积。(不溶于水、不漂浮的物体)
注意:物体一定要完全浸没在水中。
★ 完成《分层作业》;
★★ 实验活动,可以选择合适的容器,测量数据,测量生活中一些不规则物体的体积。
