5.2.2 平行线的判定 课件(共34张PPT)
文档属性
| 名称 | 5.2.2 平行线的判定 课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-07 10:07:18 | ||
图片预览








文档简介
(共34张PPT)
人教版七下第五章相交线与平行线
5.2.2 平行线的判定
人教版七年级下册
重点:平行线的三个判定定理的理解与简单运用.
难点:正确使用推理的基本格式.
教学目标
1. 理解两条直线平行的条件,会用“同位角相等”“内错角相等”“同旁内角互补”的方法判定两条直线平行 .
2. 经历探索用尺规作图画一条直线的平行线,用“同位角相等”“内错角相等”“同旁内角互补”的方法判断两条直线平行 .
复习回顾
1.平行线的定义
在同一平面内,不相交的两条直线叫做平行线.
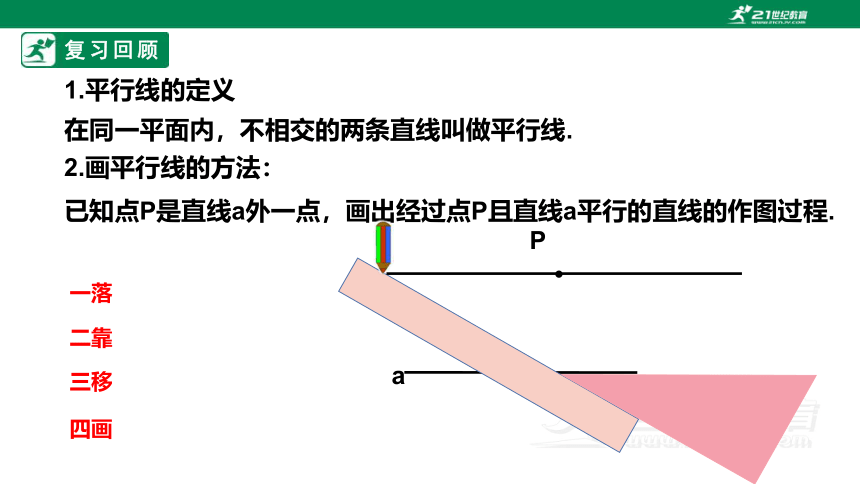
已知点P是直线a外一点,画出经过点P且直线a平行的直线的作图过程.
2.画平行线的方法:
a
P
一落
二靠
三移
四画
但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据定义来判断两条直线是否平行.
根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行.
那么,有没有其他判定方法呢?
复习回顾
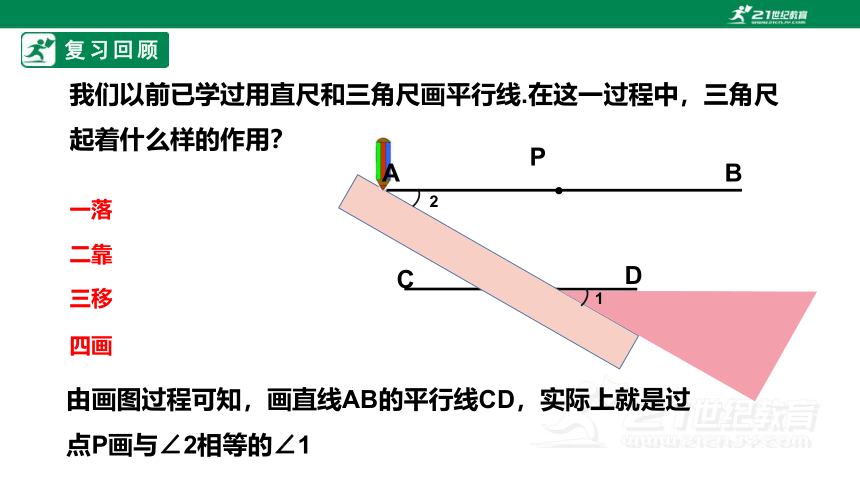
我们以前已学过用直尺和三角尺画平行线.在这一过程中,三角尺起着什么样的作用?
C
P
一落
二靠
三移
四画
由画图过程可知,画直线AB的平行线CD,实际上就是过点P画与∠2相等的∠1
1
2
D
A
B
新课引入
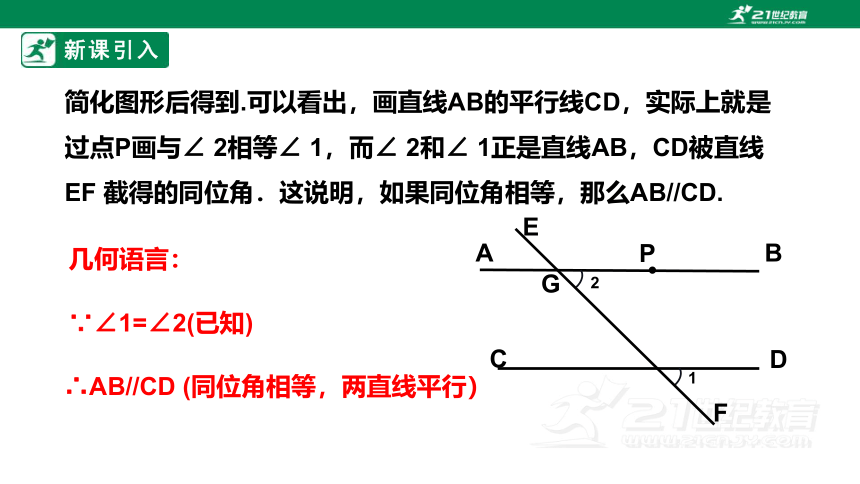
简化图形后得到.可以看出,画直线AB的平行线CD,实际上就是过点P画与∠ 2相等∠ 1,而∠ 2和∠ 1正是直线AB,CD被直线EF 截得的同位角.这说明,如果同位角相等,那么AB//CD.
C
P
1
2
D
A
B
E
F
G
∵∠1=∠2(已知)
∴AB//CD (同位角相等,两直线平行)
几何语言:
新知讲解
平行线的判定方法1:
利用同位角判定两条直线平行
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单可以说成:同位角相等,两条直线平行
新知讲解
你能说出木工师傅用图中的角尺工具画平行线的道理吗?
∵∠BEF=∠BCD(已知)
∴EF//CD (同位角相等,两直线平行)
新知讲解
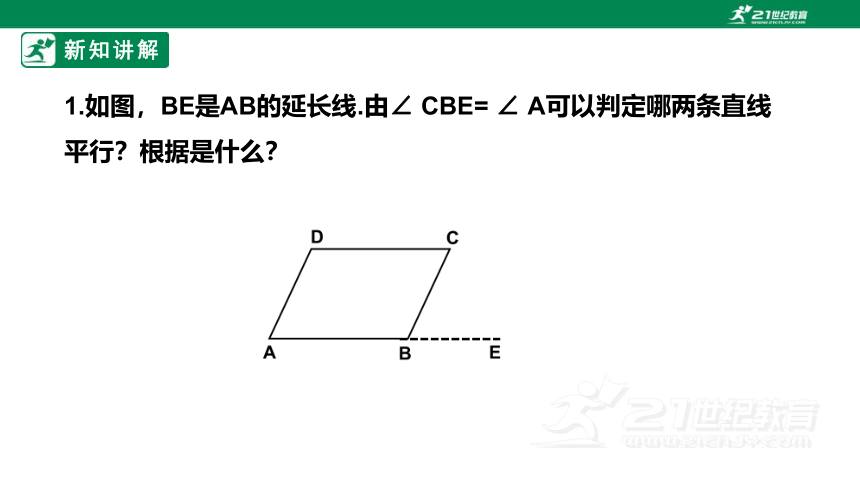
1.如图,BE是AB的延长线.由∠ CBE= ∠ A可以判定哪两条直线平行?根据是什么?
新知讲解
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
如图,由∠2=∠3,可推出a//b吗?如何推出?
1
4
a
b
c
3
2
解:∵∠2=∠3(已知)
∴ ∠1=∠3( )
对顶角相等
∴ ∠1=∠2( )
∴ a//b( )
等量代换
同位角相等,两直线平行
新知讲解
平行线的判定方法2:
利用内错角判定两条直线平行
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单可以说成:内错角相等,两条直线平行
∵∠3=∠2(已知)
∴a//b (内错角相等,两直线平行)
几何语言:
1
4
a
b
c
3
2
新知讲解
探究:遇到一个新问题时,常常把它转化为已知的(或已解决的)问题.这一节中,我们是怎样利用“同位角相等,两直线平行”得到“内错角相等,两直线平行”的?你能利用“同位角相等,两直线平行”或“内错角相等,两直线平行"得到"同旁内角互补,两直线平行"吗?
新知讲解
如图,如果∠1+∠2 =180° ,你能判定a//b吗
1
a
b
c
3
2
解:能
∵∠1+∠2=180° ( )
∠1+∠3=180° ( )
邻补角的性质
已知
∴ ∠2=∠3( )
等量代换
∴ a//b( )
同位角相等,两直线平行
新知讲解
如图,如果∠1+∠2 =180° ,你能判定a//b吗
1
a
b
c
3
2
解:能
∵∠1+∠2=180° ( )
∠1+∠3=180° ( )
邻补角的性质
已知
∴ ∠2=∠3( )
等量代换
∴ a//b( )
内错角相等,两直线平行
新知讲解
1.如图,BE是AB的延长线. 由∠ CBE= ∠ C可以判定哪两条直线平行?根据是什么?
新知讲解
平行线的判定方法3:
利用同旁内角互补判定两条直线平行
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单可以说成:同旁内角互补,两条直线平行
∵∠1+∠2=180° (已知)
∴a//b (同旁内角互补,两直线平行)
几何语言:
1
a
b
c
3
2
练一练
如图,BE 平分 ∠ABC,CE 平分 ∠DCB,∠1+ ∠2=90°,能判断AB//CD 吗 并说明理由.
解答:AB//CD.理由如下:
∵ BE 平分∠ABC,CE 平分∠DCB
∴ ∠ABC=2∠1,∠DCB=2∠2
又 ∠1+∠2=90°,
∴ ∠ABC+∠DCB=180°
∴ AB//CD(同旁内角互补,两直线平行)
新知讲解
例 在同一平面内,如果两条直线都垂直于同例一条直线,那么这两条直线平行吗?为什么?
分析:垂直总与直角联系在一起,进而用判断两条直线平行的方法进行判定.
1
a
b
c
2
∟
∟
新知讲解
你还能利用其他方法说明b//c吗?
答:这两条直线平行.理由如下:
∵ b⊥a
∴ ∠1=90°.
同理 ∠ 2=90°.
∴ ∠1=∠2.
∵∠1和∠2是同位角,
∴b//c(同位角相等,两直线平行).
1
a
b
c
2
∟
∟
课堂练习
1. 如图,过直线外一点作已知直线的平行线,其依据是( )
A. 同旁内角互补,两直线平行
B. 内错角相等,两直线平行
C. 两点确定一条直线
D. 同位角相等,两直线平行
D
课堂练习
2. 如图,∠1=78°,∠2=102°,则直线a,b的位置关系是( ).
A.相交 B.平行 C.垂直 D.无法确定
B
课堂练习
3.如图,下列判断正确的是( ).
A.若∠1+∠2=180°,则
B.若∠2=∠3,则
C.若∠1+∠2+∠3=180°,则
D.若∠2+∠4=180°,则
D
课堂练习
4. 在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线AB , CD , 贝贝、晶晶、欢欢三位同学的做法如图所示:
上述三位同学的做法中,依据“内错角相等,两直线平行”的是( )
仅贝贝同学 B. 贝贝和晶晶
C. 晶晶和欢欢 D. 贝贝和欢欢
D
课堂练习
5. 如图,能判定EC//AB的条件是( )
A. ∠B=∠ACE B. ∠A=∠ECD C. ∠B=∠ACB D. ∠A=∠ACE
D
课堂练习
6.一辆汽车在公路上行驶,要使两次拐弯后,仍在原来的方向上行驶,若第一次右转50°,则第二次拐弯的角度可能为( )
A.右转40°
B.左转100°
C.左转130°
D.左转50°
D
课堂练习
7. 如图,下列条件,不能判定AB//DC的是( )
A. ∠1=∠2
B. ∠3=∠4
C. ∠2+∠3+∠A=180^
D. ∠4+∠1=∠5
A
课堂练习
8.如图AF 与BD相交于点C,∠B=∠ACB, 且CD平分∠ECF.求证: AB//CE . 请完成下列推理过程:
证明:∵CD 平分∠ECF
∴∠ECD= ( )
∵∠ACB=∠FCD( )
∴∠ECD=∠ACB( )
∵∠B=∠ACB
∴∠B= ( )
∴AB//CE ( ).
∠FCD
角平分线的定义
对顶角相等
等量代换
∠ACB
等量代换
同位角相等,两直线平行
证明:
∵∠B+∠BAD=180°(已知),
∠1+∠BAD=180°( ),
∴∠1=∠B( ).
∵∠1=∠2(已知),
∴∠2= ( ).
∴AB//CD( ).
课堂练习
9. 如图,∠B+∠BAD=180°,∠1=∠2. 求证:AB//CD.请将下面的证明过程补充完整.
平角定义
同角的补角相等
∠B
等量代换
同位角相等,两条直线平行
课堂练习
10. 如图,已知AC平分∠EAG,BD平分∠FBG,∠1=35°,∠2=35°,那么直线AC与BD平行吗?直线AE与BF平行吗?
课堂练习
解:AC//BD,AE//BF.理由如下:
∵∠1=∠2(已知),
∴AC//BD(同位角相等,两直线平行),
∵AC平分∠EAG,BD平分∠FBG(已知),
∴∠EAG=2∠1,∠FBG=2∠2(角平分线的定义),
∴∠EAG=∠FBG(等量代换).
∴AE//BF(同位角相等,两直线平行)
课堂总结
本节课,你学习了哪些平行线的判定方法?
平行线的判定方法1:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
平行线的判定方法2:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
平行线的判定方法3:
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
课外作业
习题5.2
第15页第4题
第16页第7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版七下第五章相交线与平行线
5.2.2 平行线的判定
人教版七年级下册
重点:平行线的三个判定定理的理解与简单运用.
难点:正确使用推理的基本格式.
教学目标
1. 理解两条直线平行的条件,会用“同位角相等”“内错角相等”“同旁内角互补”的方法判定两条直线平行 .
2. 经历探索用尺规作图画一条直线的平行线,用“同位角相等”“内错角相等”“同旁内角互补”的方法判断两条直线平行 .
复习回顾
1.平行线的定义
在同一平面内,不相交的两条直线叫做平行线.
已知点P是直线a外一点,画出经过点P且直线a平行的直线的作图过程.
2.画平行线的方法:
a
P
一落
二靠
三移
四画
但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据定义来判断两条直线是否平行.
根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行.
那么,有没有其他判定方法呢?
复习回顾
我们以前已学过用直尺和三角尺画平行线.在这一过程中,三角尺起着什么样的作用?
C
P
一落
二靠
三移
四画
由画图过程可知,画直线AB的平行线CD,实际上就是过点P画与∠2相等的∠1
1
2
D
A
B
新课引入
简化图形后得到.可以看出,画直线AB的平行线CD,实际上就是过点P画与∠ 2相等∠ 1,而∠ 2和∠ 1正是直线AB,CD被直线EF 截得的同位角.这说明,如果同位角相等,那么AB//CD.
C
P
1
2
D
A
B
E
F
G
∵∠1=∠2(已知)
∴AB//CD (同位角相等,两直线平行)
几何语言:
新知讲解
平行线的判定方法1:
利用同位角判定两条直线平行
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单可以说成:同位角相等,两条直线平行
新知讲解
你能说出木工师傅用图中的角尺工具画平行线的道理吗?
∵∠BEF=∠BCD(已知)
∴EF//CD (同位角相等,两直线平行)
新知讲解
1.如图,BE是AB的延长线.由∠ CBE= ∠ A可以判定哪两条直线平行?根据是什么?
新知讲解
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
如图,由∠2=∠3,可推出a//b吗?如何推出?
1
4
a
b
c
3
2
解:∵∠2=∠3(已知)
∴ ∠1=∠3( )
对顶角相等
∴ ∠1=∠2( )
∴ a//b( )
等量代换
同位角相等,两直线平行
新知讲解
平行线的判定方法2:
利用内错角判定两条直线平行
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单可以说成:内错角相等,两条直线平行
∵∠3=∠2(已知)
∴a//b (内错角相等,两直线平行)
几何语言:
1
4
a
b
c
3
2
新知讲解
探究:遇到一个新问题时,常常把它转化为已知的(或已解决的)问题.这一节中,我们是怎样利用“同位角相等,两直线平行”得到“内错角相等,两直线平行”的?你能利用“同位角相等,两直线平行”或“内错角相等,两直线平行"得到"同旁内角互补,两直线平行"吗?
新知讲解
如图,如果∠1+∠2 =180° ,你能判定a//b吗
1
a
b
c
3
2
解:能
∵∠1+∠2=180° ( )
∠1+∠3=180° ( )
邻补角的性质
已知
∴ ∠2=∠3( )
等量代换
∴ a//b( )
同位角相等,两直线平行
新知讲解
如图,如果∠1+∠2 =180° ,你能判定a//b吗
1
a
b
c
3
2
解:能
∵∠1+∠2=180° ( )
∠1+∠3=180° ( )
邻补角的性质
已知
∴ ∠2=∠3( )
等量代换
∴ a//b( )
内错角相等,两直线平行
新知讲解
1.如图,BE是AB的延长线. 由∠ CBE= ∠ C可以判定哪两条直线平行?根据是什么?
新知讲解
平行线的判定方法3:
利用同旁内角互补判定两条直线平行
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单可以说成:同旁内角互补,两条直线平行
∵∠1+∠2=180° (已知)
∴a//b (同旁内角互补,两直线平行)
几何语言:
1
a
b
c
3
2
练一练
如图,BE 平分 ∠ABC,CE 平分 ∠DCB,∠1+ ∠2=90°,能判断AB//CD 吗 并说明理由.
解答:AB//CD.理由如下:
∵ BE 平分∠ABC,CE 平分∠DCB
∴ ∠ABC=2∠1,∠DCB=2∠2
又 ∠1+∠2=90°,
∴ ∠ABC+∠DCB=180°
∴ AB//CD(同旁内角互补,两直线平行)
新知讲解
例 在同一平面内,如果两条直线都垂直于同例一条直线,那么这两条直线平行吗?为什么?
分析:垂直总与直角联系在一起,进而用判断两条直线平行的方法进行判定.
1
a
b
c
2
∟
∟
新知讲解
你还能利用其他方法说明b//c吗?
答:这两条直线平行.理由如下:
∵ b⊥a
∴ ∠1=90°.
同理 ∠ 2=90°.
∴ ∠1=∠2.
∵∠1和∠2是同位角,
∴b//c(同位角相等,两直线平行).
1
a
b
c
2
∟
∟
课堂练习
1. 如图,过直线外一点作已知直线的平行线,其依据是( )
A. 同旁内角互补,两直线平行
B. 内错角相等,两直线平行
C. 两点确定一条直线
D. 同位角相等,两直线平行
D
课堂练习
2. 如图,∠1=78°,∠2=102°,则直线a,b的位置关系是( ).
A.相交 B.平行 C.垂直 D.无法确定
B
课堂练习
3.如图,下列判断正确的是( ).
A.若∠1+∠2=180°,则
B.若∠2=∠3,则
C.若∠1+∠2+∠3=180°,则
D.若∠2+∠4=180°,则
D
课堂练习
4. 在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线AB , CD , 贝贝、晶晶、欢欢三位同学的做法如图所示:
上述三位同学的做法中,依据“内错角相等,两直线平行”的是( )
仅贝贝同学 B. 贝贝和晶晶
C. 晶晶和欢欢 D. 贝贝和欢欢
D
课堂练习
5. 如图,能判定EC//AB的条件是( )
A. ∠B=∠ACE B. ∠A=∠ECD C. ∠B=∠ACB D. ∠A=∠ACE
D
课堂练习
6.一辆汽车在公路上行驶,要使两次拐弯后,仍在原来的方向上行驶,若第一次右转50°,则第二次拐弯的角度可能为( )
A.右转40°
B.左转100°
C.左转130°
D.左转50°
D
课堂练习
7. 如图,下列条件,不能判定AB//DC的是( )
A. ∠1=∠2
B. ∠3=∠4
C. ∠2+∠3+∠A=180^
D. ∠4+∠1=∠5
A
课堂练习
8.如图AF 与BD相交于点C,∠B=∠ACB, 且CD平分∠ECF.求证: AB//CE . 请完成下列推理过程:
证明:∵CD 平分∠ECF
∴∠ECD= ( )
∵∠ACB=∠FCD( )
∴∠ECD=∠ACB( )
∵∠B=∠ACB
∴∠B= ( )
∴AB//CE ( ).
∠FCD
角平分线的定义
对顶角相等
等量代换
∠ACB
等量代换
同位角相等,两直线平行
证明:
∵∠B+∠BAD=180°(已知),
∠1+∠BAD=180°( ),
∴∠1=∠B( ).
∵∠1=∠2(已知),
∴∠2= ( ).
∴AB//CD( ).
课堂练习
9. 如图,∠B+∠BAD=180°,∠1=∠2. 求证:AB//CD.请将下面的证明过程补充完整.
平角定义
同角的补角相等
∠B
等量代换
同位角相等,两条直线平行
课堂练习
10. 如图,已知AC平分∠EAG,BD平分∠FBG,∠1=35°,∠2=35°,那么直线AC与BD平行吗?直线AE与BF平行吗?
课堂练习
解:AC//BD,AE//BF.理由如下:
∵∠1=∠2(已知),
∴AC//BD(同位角相等,两直线平行),
∵AC平分∠EAG,BD平分∠FBG(已知),
∴∠EAG=2∠1,∠FBG=2∠2(角平分线的定义),
∴∠EAG=∠FBG(等量代换).
∴AE//BF(同位角相等,两直线平行)
课堂总结
本节课,你学习了哪些平行线的判定方法?
平行线的判定方法1:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
平行线的判定方法2:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
平行线的判定方法3:
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
课外作业
习题5.2
第15页第4题
第16页第7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
