单元培优易错题第二单元:比例-六年级下册数学培优卷(北师大版)(含答案)
文档属性
| 名称 | 单元培优易错题第二单元:比例-六年级下册数学培优卷(北师大版)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 297.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-07 00:00:00 | ||
图片预览




文档简介
单元培优易错题第二单元:比例
六年级下册数学培优卷(北师大版)
学校:___________姓名:___________班级:___________
一、选择题
1.下面各组比中,能与。组成比例的是( )。
A.10∶14 B.12∶14 C. D.8∶7
2.甲数的与乙数的相等(甲,乙两数均不为0),则甲∶乙=( )。
A.9∶8 B.8∶9 C.6∶2 D.1∶2
3.用2,3,6,9组成的比例中,正确的是( )。
A. B. C.
4.下面各组中的两个比,可以组成比例的是( )。
A.8∶3和8.2∶3.2 B.∶8和8∶
C.1.2∶和∶5 D.10∶6和25∶15
5.能与组成比例的是( )。
A.4∶3 B.3∶4 C.∶3 D.3∶
6.甲数的等于乙数的,甲数与乙数的比是( )。
A.3∶10 B.5∶2 C.10∶3 D.5∶16
7.一座大桥全长12.8千米,在一幅地图上量得它的长是6.4厘米,这幅地图的比例尺是( )。
A.2000∶1 B.200000∶1 C.1∶2000 D.1∶200000
8.在比例尺是1∶20的图纸上画出一种机械配件平面图的角是40度。这个角实际是( )度。
A.2 B.20 C.40 D.80
二、填空题
9.在3∶2=12∶8这个比例中,两个外项是( )和( ),两个内项是( )和( )。
10.一幅地图的比例尺是,在这幅地图上量得甲、乙两地间的公路长12厘米,一辆汽车上午10时以80千米/时的平均速度从甲地出发,如果中途不休息,下午( )时可以到达乙地。
11.量得一个零件长2.5厘米,宽1厘米,在比例尺是5∶1的图纸上,长应该画_________厘米,宽应该画_________厘米。
12.一种微型零件长5mm,画在图纸上的长是2cm,这幅图的比例尺是( ),图上1cm相当于实际距离( )。
13.在一幅比例尺1∶4000000的中国地图上量得A、B两地相距5.5厘米,A、B两地实际相距( )千米。
14.如果a×6=b×8,那么a∶b=( )∶( )。
15.在一个比例中,两个内项之积互为倒数,其中一个外项是0.6,另一个外项是( )。
16.一个精密零件,在比例尺是20∶1的图纸上,量得它的长度是5厘米,这个精密零件的实际长度是( )毫米。
三、判断题
17.学校操场的实际长是240m,画在图纸上的长是6cm。这张图纸的比例尺是1∶40。( )
18.和可以组成比例。( )
19.在一个比例中,两个内项互为倒数,若其中一个外项是10以内最大的质数,则另一个外项是。( )
20.在比例中,3和是比例的外项,4.5和是比例的内项。( )
21.在一个比例中,两个外项互为倒数,其中一个内项是,另一个内项是。( )
22.一幅地图的比例尺是1∶5,它表示实际距离是图上距离的5倍。( )
23.因为4a=5b,所以,4∶5=a∶b。( )
四、计算题
24.直接写得数。
0.8∶2.4=
8π=
25.解方程。
5x-1.2x=7.6 x∶80%=4∶0.4 x∶6.4=∶
26.解方程或比例。
8∶x=2.4∶0.9 2y-30%y=34
五、解答题
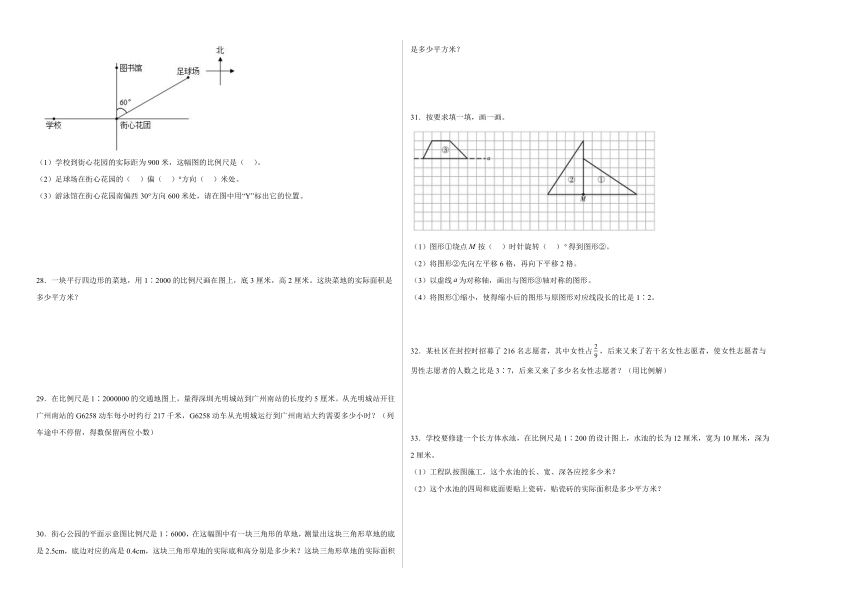
27.按要求填空。(测量图上距高时取整厘米)
(1)学校到街心花园的实际距为900米,这幅图的比例尺是( )。
(2)足球场在街心花园的( )偏( )°方向( )米处。
(3)游泳馆在街心花园南偏西30°方向600米处,请在图中用“Y”标出它的位置。
一块平行四边形的菜地,用1∶2000的比例尺画在图上,底3厘米,高2厘米。这块菜地的实际面积是多少平方米?
在比例尺是1∶2000000的交通地图上,量得深圳光明城站到广州南站的长度约5厘米。从光明城站开往广州南站的G6258动车每小时约行217千米,G6258动车从光明城运行到广州南站大约需要多少小时?(列车途中不停留,得数保留两位小数)
街心公园的平面示意图比例尺是1∶6000,在这幅图中有一块三角形的草地,测量出这块三角形草地的底是2.5cm,底边对应的高是0.4cm,这块三角形草地的实际底和高分别是多少米?这块三角形草地的实际面积是多少平方米?
31.按要求填一填,画一画。
(1)图形①绕点按( )时针旋转( )得到图形②。
(2)将图形②先向左平移6格,再向下平移2格。
(3)以虚线为对称轴,画出与图形③轴对称的图形。
(4)将图形①缩小,使得缩小后的图形与原图形对应线段长的比是1∶2。
32.某社区在封控时招募了216名志愿者,其中女性占,后来又来了若干名女性志愿者,使女性志愿者与男性志愿者的人数之比是3∶7,后来又来了多少名女性志愿者?(用比例解)
33.学校要修建一个长方体水池,在比例尺是1∶200的设计图上,水池的长为12厘米,宽为10厘米,深为2厘米。
(1)工程队按图施工,这个水池的长、宽、深各应挖多少米?
(2)这个水池的四周和底面要贴上瓷砖,贴瓷砖的实际面积是多少平方米?
参考答案:
1.D
【分析】根据比例的基本性质:比例的两个内项之积等于两个外项之积,据此解答。
【详解】A.∶与10∶14;
×14=2;×10=
2≠;所以∶与10∶14不能组成比例;
B.∶与12∶14
×14=2;×12=
2≠,所以∶与12∶14不能组成比例;
C.∶与∶
×=;×=
≠;所以∶与∶不能组成比例;
D.∶与8∶7
×7=1;×8=1
1=1;所以∶与8∶7能组成比例。
故答案为:D
利用比例的基本性质进行解答。
2.A
【分析】甲数的与乙数的相等(甲、乙两数均不为0),得出甲数×=乙数×(甲、乙两数均不为0),再利用比例的基本性质以及比的性质,求出甲数∶乙数的值。
【详解】甲数×=乙数×
甲数∶乙数=∶
=(×12)∶(×12)
=9∶8
故答案为:A
利用比例的基本性质和比的性质进行解答。
3.B
【分析】根据比例的基本性质:在比例里,两个内项的积等于两个外项的积;如果两个数的积等于另两个数的积,那么这四个数就能组成比例,据此解答。
【详解】A.2∶3=9∶6
2×6=12
3×9=27
12≠27
2∶3与9∶6不成比例;
B.2∶3=6∶9
2×9=18
3×6=18
18=18
2∶3与6∶9成比例;
C.3∶2=6∶9
3×9=27
2×6=12
27≠12
3∶2与6∶9不成比例。
故答案为:B
本题考查比例的基本性质,根据比例的基本性质进行解答。
4.D
【分析】根据比例的基本性质作答,即在比例里,两个外项的积等于两个内项的积,由此逐项判断即可。
【详解】A.3×8.2=24.6,8×3.2=25.6,因为24.6≠25.6,所以8∶3和8.2∶3.2不能组成比例;
B.8×8=64,×=,因为64≠,所以∶8和8∶不能组成比例;
C.1.2×5=6,×=,因为6≠,所以1.2∶和∶5不能组成比例;
D.10×15=150,6×25=150,因为150=150,所以10∶6和25∶15能组成比例。
故答案为:D
本题主要考查比例的意义和基本性质,也可以用求比值的方法,求出比值,比值相等两个比就能组成比例。
5.A
【分析】比例的基本概念,比值相等的两个比组成比例,算出各项的比值,据此判断即可。
【详解】=÷=
A.4∶3=4÷3=;=,能组成比例;
B.3∶4=3÷4=;≠,不能组成比例;
C.∶3=÷3=;≠,不能组成比例;
D.3∶=3÷=12;12≠,不能组成比例。
故答案为:A
根据比例的意义进行解答。
6.C
【分析】根据题意,甲数×=乙数×,逆着用比例的基本性质,两个外项的积等于两个内项的积,求出两数之比即可。
【详解】因为甲数×=乙数×,
则甲数∶乙数=∶=10∶3。
故答案为:C
此题主要考查比例基本性质的灵活应用,把乘积相等的两个乘法写成比例的形式是解题的关键。
7.D
【分析】根据比例尺=图上距离∶实际距离,代入数据解答即可。
【详解】6.4厘米∶12.8千米
=6.4厘米∶1280000厘米
=1∶200000
故答案为:D
解答此题的关键是掌握比例尺、图上距离和实际距离三者之间的关系。
8.C
【分析】根据:比例尺=图上距离÷实际距离,是指长度尺寸按比例放大或缩小。
【详解】根据比例尺是1∶20的图纸,知道图上距离是1厘米,实际距离是20厘米,
是长度尺寸是按比例缩小,角的大小与边的长度无关,只与两边叉开的程度有关,
所以角的度数是不会变的。
故答案为:C
本题主要考查了比例尺的意义以及角的意义。
9. 3 8 2 12
【详解】离等号较远的两个数是3和8,故3和8是外项,靠近等号的两个数是2和12,故2和12是内项。
10.4
【分析】根据实际距离、图上距离和比例尺的关系,计算出甲、乙两地的实际距离,再根据时间=距离÷速度,代入数据,求出到达乙地的时间,即可解答。
【详解】40×12÷80
=480÷60
=6(时)
上午10时=10时
10时+6时=16时
16时=下午4时
本题考查比例尺的应用,以及时间、速度和距离三者的关系,注意普通计时法和24时计时法的换算。
11. 12.5 5
【分析】比例尺5∶1,就是图上5厘米表示实际的1厘米,把零件的长和宽都扩大到原来的5倍即可。
【详解】长:2.5×5=12.5(厘米)
宽:1×5=5(厘米)
此题主要考查学生对图形按比例放大的应用。
12. 4∶1 2.5mm
【分析】根据比例尺=图上距离∶实际距离列式解答即可。
【详解】比例尺为:
2cm=20mm
20∶5=4∶1
图上1cm相当于实际距离为:
1÷=0.25(cm)
0.25cm=2.5mm
利用比例尺的意义,实际距离与图上距离的互换解答本题,注意单位的统一。
13.220
【分析】要求甲、乙两城市的实际距离是多少千米,根据“图上距离÷比例尺=实际距离”,代入数值计算即可。
【详解】5.5÷=22000000(厘米)
22000000厘米=220千米
此题有计算公式可用,根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论。
14. 4 3
【分析】根据比例的基本性质,两内项之积等于两外项之积,把b和8当做比例的内项,把a和6当做比例的外项,写出比例后化简即可。
【详解】a×6=b×8,
a∶b=8∶6
a∶b=(8÷2)∶(6÷2)
a∶b=4∶3。
熟练掌握比例的基本性质是解答本题的关键。
15.
【分析】根据倒数的意义:乘积是1的两个数互为倒数;比例的基本性质:两个外项之积等于两个内项之积;把0.6化成分数,即可解答。
【详解】0.6=
1÷
=1×
=
利用倒数的意义,比例的基本性质进行解答。
16.2.5
【分析】根据图上距离÷比例尺=实际距离,进行换算即可。
【详解】5厘米=50毫米
50÷20=2.5(毫米)
关键是理解比例尺的意义,掌握图上距离与实际距离的换算方法。
17.×
【分析】根据比例尺的意义:比例尺=图上距离∶实际距离,代入数据,即可解答。
【详解】240m=24000cm
6∶24000
=(6÷6)∶(24000÷6)
=1∶4000
学校操场的实际长是240m,画在图纸上的长是6cm。这张图纸的比例尺是1∶4000。
故答案为:×
利用比例尺的意义进行解答;注意单位名数的统一。
18.×
【分析】根据比例的基本性质:比例的两个内项之积等于两个外项之积,据此解答。
【详解】∶和∶2
×2=
×=
≠,所以∶和∶2不能组成比例。
原题干说法错误。
故答案为:×
熟练掌握比例的基本性质是解答本题的关键。
19.×
【分析】首先明确:10以内最大的质数是7,再结合比例的基本性质和倒数的意义解答即可。
【详解】因为两个内项互为倒数,所以两个内项的积是1,两个外项的积是1。
10以内最大的质数是7,因为7的倒数是,所以另一个外项是。
故答案为:×
此题考查比例性质的应用:两个内项之积等于两个外项之积。
20.√
【分析】组成比例两端的两项叫做外项,中间的两项叫做内项,据此判断。
【详解】在比例中,3和是比例的外项,4.5和是比例的内项;所以原题说法正确。
故答案为:√
本题主要考查了比例的意义,解题的关键是熟记组成比例两端的两项叫做外项,中间的两项叫做内项。
21.×
【分析】根据倒数的意义,互为倒数的两个数乘积是1,两个外项互为倒数,那么它们的乘积是1。根据比例的基本性质,用两外项之积除以其中一个内项,可求出另一个内项。
【详解】由分析可知:
1÷=
所以另一个内项是 。
故答案为:×
本题考查了倒数的认识以及比例的基本性质,比例的两外项之积等于两内项之积。
22.√
【分析】根据数值比例尺的意义可知:一幅地图的比例尺是1∶5,表示图上1厘米代表实际距离5厘米。
【详解】5÷1=5
一幅地图的比例尺是1∶5,它表示实际距离是图上距离的5倍;此说法正确。
故答案为:√
本题主要考查学生对数值比例尺意义的理解。
23.×
【分析】在比例中,两内项积等于两外项积,据此判断。
【详解】因为4a=5b,可把4和a看作比例的外项,5和b看作比例的内项,所以4∶5=b∶a。原题说法错误。
故答案为:×
此题考查了比例的基本性质,要学会灵活运用。
24.27;4;;0.5;
40;;25.52;0.01。
【分析】根据小数、分数、百分数的加减乘除运算以及求比值的计算方法解答。
【详解】8.1÷0.3=27 32×12.5%=4 0.8∶2.4= 0.3+=0.5
44÷=40 ×= 8=25.52 0.1=0.01
考查了四则运算,关键是熟练掌握计算法则正确进行计算。
25.x=2;x=8;x=5.6
【分析】(1)先把方程左边化简为3.8x,两边再同时除以3.8;
(2)根据比例的基本性质,把比例化为方程,两边再同时除以0.4;
(3)根据比例的基本性质,把比例化为方程,两边再同时乘7。
【详解】(1)5x-1.2x=7.6
解:3.8x=7.6
3.8x÷3.8=7.6÷3.8
x=2
(2)x∶80%=4∶0.4
解:0.4x=3.2
0.4x÷0.4=3.2÷0.4
x=8
(3)x∶6.4=∶
解:x×=6.4×
x=0.8
7×x=0.8×7
x=5.6
26.x=24;x=3;y=20
【分析】(1)方程两边先同时减去9,然后两边同时除以。
(2)将比例式化成方程后两边同时除以2.4。
(3)先化简2y-30%y,然后方程的两边同时除以(2-30%)的差。
【详解】(1)x+9=30
解:x+9-9=30-9
x=21
x÷=21÷
x=24
(2)8∶x=2.4∶0.9
解:2.4x=8×0.9
2.4x=7.2
2.4x÷2.4=7.2÷2.4
x=3
(3)2y-30%y=34
解:2y-0.3y=34
1.7y=34
1.7y÷1.7=34÷1.7
y=20
27.(1)1∶30000
(2)东,北60;1200
(3)见详解
【分析】(1)用尺子测量,即可知道学校到街心花园的距离是3厘米,实际距离是900米,根据比例尺的公式:比例尺=图上距离∶实际距离,把数代入公式即可求解,要注意统一单位。
(2)根据地图上的方向(上北下南,左西右东),即可找出足球场在街心花园的方向,之后量出街心花园到足球场的图上距离,再根据公式:实际距离=图上距离÷比例尺,求出实际距离。
(3)图上距离=实际距离×比例尺,求出图上距离,再根据地图上的方向(上北下南,左西右东),即可找出游泳馆的位置。
【详解】(1)900米=90000厘米
3厘米∶90000厘米
=(3÷3)∶(90000÷3)
=1∶30000
所以这幅图的比例尺是:1∶30000
(2)足球场在街心花园图上距离4厘米处
4×30000=120000(厘米)
120000厘米=1200米
即足球场在街心花园的北偏东60°方向1200米。
(3)600米=60000厘米
60000×=2(厘米)
如下图所示:
本题主要学会找准方向,并熟练掌握图上距离和实际距离的关系是解题的关键。
28.2400平方米
【分析】根据:图上距离÷比例尺=实际距离,代入数据计算出平行四边形菜地实际的底和高,再应用平行四边形的面积公式,计算出菜地的实际面积。
【详解】3÷=3×2000=6000(厘米)=60(米)
2÷=2×2000=4000(厘米)=40(米)
60×40=2400(平方米)
答:这块菜地的实际面积是2400平方米。
理解比例尺的意义,结合平行四边形的特点,运用比例尺解决生活中的实际问题。
29.0.46小时
【分析】根据实际距离=图上距离÷比例尺,据此求出深圳光明城站到广州南站的实际距离,再利用公式:路程=时间×速度,可以求出G6258动车从光明城运行到广州南站大约需要的时间。
【详解】深圳光明城站到广州南站的实际距离为:
5÷=5×2000000=10000000(厘米)
10000000厘米=100千米
100÷217≈0.46(小时)
答:G6258动车从光明城运行到广州南站大约需要0.46小时。
此题主要考查了图上距离和实际距离之间的换算,同时也要能熟练应用路程公式。
30.150米;24米;1800平方米
【分析】根据实际距离=图上距离÷比例尺,代入数据算出这块三角形草地底和高的实际长度,再根据三角形的面积=底×高÷2计算面积即可。
【详解】三角形草地底的实际长度为:
2.5÷=15000(厘米)
15000厘米=150米
三角形草地高的实际长度为:
0.4÷=2400(厘米)
2400厘米=24米
三角形草地实际面积为:
150×24÷2
=3600÷2
=1800(平方米)
答:这块三角形草地的实际底是150米,高是24米;这块三角形草地的实际面积是1800平方米。
解答此题的关键是掌握比例尺=图上距离÷实际距离这个公式及其变形,同时要会灵活应用三角形的面积公式。
31.(1)逆;90
(2)、(3)、(4)见详解
【分析】(1)根据旋转的特征可知,图形①绕点M按逆时针旋转90°得到图形②。
(2)根据平移的特征,将图形②的3个顶点先向左平移6格,再向下平移2格,然后连接即可。
(3)根据轴对称图形的画法,以虚线a为对称轴,在对称轴的另一边画出与图形③的关键点,然后画出轴对称的图形。
(4)根据图形缩小知识,将图形①的底和高缩小至原来的二分之一,即缩小后的三角形底是6÷2=3(格),高是4÷2=2(格),形状不变,据此画图即可。
【详解】(1)图形①绕点按逆时针旋转90得到图形②。
(2)、(3)、(4)根据要求,作图如下:
本题考查了旋转、平移、图形的缩小等知识,掌握图形旋转、平移和缩小的特征是解答本题的关键。
32.24名
【分析】根据原来女性占总人数的分率,求出女性和男性的人数,再设后来来了x名女性,根据女性和男性人数比,列比例求解。
【详解】原来女性人数:216×=48(名)
男性人数:216-48=168(名)
解:设后来来了x名女性。
(48+x)∶168=3∶7
7×(48+x)=3×168
336+7x=504
336+7x-336=504-336
7x=168
7x÷7=168÷7
x=24
答:后来又来了24名女性志愿者。
本题主要考查比例的应用,关键注意男性志愿者的人数没有改变。
33.(1)长24米,宽20米,深4米
(2)832平方米
【分析】(1)图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可分别求出水池的长、宽、深的实际长度;
(2)贴瓷砖的面积,就是用表面积减去上口的面积,利用长方体表面积公式即可求解。
【详解】(1)水池实际的长:12÷=2400(厘米)=24(米)
水池实际的宽:10÷=2000(厘米)=20(米)
水池实际的深度:2÷=400(厘米)=4(米)
答:这个水池的长应挖24米、宽应挖20米、深应挖4米。
(2)(24×20+20×4+4×24)×2-24×20
=(480+80+96)×2-480
=656×2-480
=1312-480
=832(平方米)
答:这个水池的四周和底面要贴上瓷砖,贴瓷砖的实际面积是832平方米。
此题主要考查图上距离、实际距离和比例尺的关系,以及长方体的表面积公式的运用。
六年级下册数学培优卷(北师大版)
学校:___________姓名:___________班级:___________
一、选择题
1.下面各组比中,能与。组成比例的是( )。
A.10∶14 B.12∶14 C. D.8∶7
2.甲数的与乙数的相等(甲,乙两数均不为0),则甲∶乙=( )。
A.9∶8 B.8∶9 C.6∶2 D.1∶2
3.用2,3,6,9组成的比例中,正确的是( )。
A. B. C.
4.下面各组中的两个比,可以组成比例的是( )。
A.8∶3和8.2∶3.2 B.∶8和8∶
C.1.2∶和∶5 D.10∶6和25∶15
5.能与组成比例的是( )。
A.4∶3 B.3∶4 C.∶3 D.3∶
6.甲数的等于乙数的,甲数与乙数的比是( )。
A.3∶10 B.5∶2 C.10∶3 D.5∶16
7.一座大桥全长12.8千米,在一幅地图上量得它的长是6.4厘米,这幅地图的比例尺是( )。
A.2000∶1 B.200000∶1 C.1∶2000 D.1∶200000
8.在比例尺是1∶20的图纸上画出一种机械配件平面图的角是40度。这个角实际是( )度。
A.2 B.20 C.40 D.80
二、填空题
9.在3∶2=12∶8这个比例中,两个外项是( )和( ),两个内项是( )和( )。
10.一幅地图的比例尺是,在这幅地图上量得甲、乙两地间的公路长12厘米,一辆汽车上午10时以80千米/时的平均速度从甲地出发,如果中途不休息,下午( )时可以到达乙地。
11.量得一个零件长2.5厘米,宽1厘米,在比例尺是5∶1的图纸上,长应该画_________厘米,宽应该画_________厘米。
12.一种微型零件长5mm,画在图纸上的长是2cm,这幅图的比例尺是( ),图上1cm相当于实际距离( )。
13.在一幅比例尺1∶4000000的中国地图上量得A、B两地相距5.5厘米,A、B两地实际相距( )千米。
14.如果a×6=b×8,那么a∶b=( )∶( )。
15.在一个比例中,两个内项之积互为倒数,其中一个外项是0.6,另一个外项是( )。
16.一个精密零件,在比例尺是20∶1的图纸上,量得它的长度是5厘米,这个精密零件的实际长度是( )毫米。
三、判断题
17.学校操场的实际长是240m,画在图纸上的长是6cm。这张图纸的比例尺是1∶40。( )
18.和可以组成比例。( )
19.在一个比例中,两个内项互为倒数,若其中一个外项是10以内最大的质数,则另一个外项是。( )
20.在比例中,3和是比例的外项,4.5和是比例的内项。( )
21.在一个比例中,两个外项互为倒数,其中一个内项是,另一个内项是。( )
22.一幅地图的比例尺是1∶5,它表示实际距离是图上距离的5倍。( )
23.因为4a=5b,所以,4∶5=a∶b。( )
四、计算题
24.直接写得数。
0.8∶2.4=
8π=
25.解方程。
5x-1.2x=7.6 x∶80%=4∶0.4 x∶6.4=∶
26.解方程或比例。
8∶x=2.4∶0.9 2y-30%y=34
五、解答题
27.按要求填空。(测量图上距高时取整厘米)
(1)学校到街心花园的实际距为900米,这幅图的比例尺是( )。
(2)足球场在街心花园的( )偏( )°方向( )米处。
(3)游泳馆在街心花园南偏西30°方向600米处,请在图中用“Y”标出它的位置。
一块平行四边形的菜地,用1∶2000的比例尺画在图上,底3厘米,高2厘米。这块菜地的实际面积是多少平方米?
在比例尺是1∶2000000的交通地图上,量得深圳光明城站到广州南站的长度约5厘米。从光明城站开往广州南站的G6258动车每小时约行217千米,G6258动车从光明城运行到广州南站大约需要多少小时?(列车途中不停留,得数保留两位小数)
街心公园的平面示意图比例尺是1∶6000,在这幅图中有一块三角形的草地,测量出这块三角形草地的底是2.5cm,底边对应的高是0.4cm,这块三角形草地的实际底和高分别是多少米?这块三角形草地的实际面积是多少平方米?
31.按要求填一填,画一画。
(1)图形①绕点按( )时针旋转( )得到图形②。
(2)将图形②先向左平移6格,再向下平移2格。
(3)以虚线为对称轴,画出与图形③轴对称的图形。
(4)将图形①缩小,使得缩小后的图形与原图形对应线段长的比是1∶2。
32.某社区在封控时招募了216名志愿者,其中女性占,后来又来了若干名女性志愿者,使女性志愿者与男性志愿者的人数之比是3∶7,后来又来了多少名女性志愿者?(用比例解)
33.学校要修建一个长方体水池,在比例尺是1∶200的设计图上,水池的长为12厘米,宽为10厘米,深为2厘米。
(1)工程队按图施工,这个水池的长、宽、深各应挖多少米?
(2)这个水池的四周和底面要贴上瓷砖,贴瓷砖的实际面积是多少平方米?
参考答案:
1.D
【分析】根据比例的基本性质:比例的两个内项之积等于两个外项之积,据此解答。
【详解】A.∶与10∶14;
×14=2;×10=
2≠;所以∶与10∶14不能组成比例;
B.∶与12∶14
×14=2;×12=
2≠,所以∶与12∶14不能组成比例;
C.∶与∶
×=;×=
≠;所以∶与∶不能组成比例;
D.∶与8∶7
×7=1;×8=1
1=1;所以∶与8∶7能组成比例。
故答案为:D
利用比例的基本性质进行解答。
2.A
【分析】甲数的与乙数的相等(甲、乙两数均不为0),得出甲数×=乙数×(甲、乙两数均不为0),再利用比例的基本性质以及比的性质,求出甲数∶乙数的值。
【详解】甲数×=乙数×
甲数∶乙数=∶
=(×12)∶(×12)
=9∶8
故答案为:A
利用比例的基本性质和比的性质进行解答。
3.B
【分析】根据比例的基本性质:在比例里,两个内项的积等于两个外项的积;如果两个数的积等于另两个数的积,那么这四个数就能组成比例,据此解答。
【详解】A.2∶3=9∶6
2×6=12
3×9=27
12≠27
2∶3与9∶6不成比例;
B.2∶3=6∶9
2×9=18
3×6=18
18=18
2∶3与6∶9成比例;
C.3∶2=6∶9
3×9=27
2×6=12
27≠12
3∶2与6∶9不成比例。
故答案为:B
本题考查比例的基本性质,根据比例的基本性质进行解答。
4.D
【分析】根据比例的基本性质作答,即在比例里,两个外项的积等于两个内项的积,由此逐项判断即可。
【详解】A.3×8.2=24.6,8×3.2=25.6,因为24.6≠25.6,所以8∶3和8.2∶3.2不能组成比例;
B.8×8=64,×=,因为64≠,所以∶8和8∶不能组成比例;
C.1.2×5=6,×=,因为6≠,所以1.2∶和∶5不能组成比例;
D.10×15=150,6×25=150,因为150=150,所以10∶6和25∶15能组成比例。
故答案为:D
本题主要考查比例的意义和基本性质,也可以用求比值的方法,求出比值,比值相等两个比就能组成比例。
5.A
【分析】比例的基本概念,比值相等的两个比组成比例,算出各项的比值,据此判断即可。
【详解】=÷=
A.4∶3=4÷3=;=,能组成比例;
B.3∶4=3÷4=;≠,不能组成比例;
C.∶3=÷3=;≠,不能组成比例;
D.3∶=3÷=12;12≠,不能组成比例。
故答案为:A
根据比例的意义进行解答。
6.C
【分析】根据题意,甲数×=乙数×,逆着用比例的基本性质,两个外项的积等于两个内项的积,求出两数之比即可。
【详解】因为甲数×=乙数×,
则甲数∶乙数=∶=10∶3。
故答案为:C
此题主要考查比例基本性质的灵活应用,把乘积相等的两个乘法写成比例的形式是解题的关键。
7.D
【分析】根据比例尺=图上距离∶实际距离,代入数据解答即可。
【详解】6.4厘米∶12.8千米
=6.4厘米∶1280000厘米
=1∶200000
故答案为:D
解答此题的关键是掌握比例尺、图上距离和实际距离三者之间的关系。
8.C
【分析】根据:比例尺=图上距离÷实际距离,是指长度尺寸按比例放大或缩小。
【详解】根据比例尺是1∶20的图纸,知道图上距离是1厘米,实际距离是20厘米,
是长度尺寸是按比例缩小,角的大小与边的长度无关,只与两边叉开的程度有关,
所以角的度数是不会变的。
故答案为:C
本题主要考查了比例尺的意义以及角的意义。
9. 3 8 2 12
【详解】离等号较远的两个数是3和8,故3和8是外项,靠近等号的两个数是2和12,故2和12是内项。
10.4
【分析】根据实际距离、图上距离和比例尺的关系,计算出甲、乙两地的实际距离,再根据时间=距离÷速度,代入数据,求出到达乙地的时间,即可解答。
【详解】40×12÷80
=480÷60
=6(时)
上午10时=10时
10时+6时=16时
16时=下午4时
本题考查比例尺的应用,以及时间、速度和距离三者的关系,注意普通计时法和24时计时法的换算。
11. 12.5 5
【分析】比例尺5∶1,就是图上5厘米表示实际的1厘米,把零件的长和宽都扩大到原来的5倍即可。
【详解】长:2.5×5=12.5(厘米)
宽:1×5=5(厘米)
此题主要考查学生对图形按比例放大的应用。
12. 4∶1 2.5mm
【分析】根据比例尺=图上距离∶实际距离列式解答即可。
【详解】比例尺为:
2cm=20mm
20∶5=4∶1
图上1cm相当于实际距离为:
1÷=0.25(cm)
0.25cm=2.5mm
利用比例尺的意义,实际距离与图上距离的互换解答本题,注意单位的统一。
13.220
【分析】要求甲、乙两城市的实际距离是多少千米,根据“图上距离÷比例尺=实际距离”,代入数值计算即可。
【详解】5.5÷=22000000(厘米)
22000000厘米=220千米
此题有计算公式可用,根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论。
14. 4 3
【分析】根据比例的基本性质,两内项之积等于两外项之积,把b和8当做比例的内项,把a和6当做比例的外项,写出比例后化简即可。
【详解】a×6=b×8,
a∶b=8∶6
a∶b=(8÷2)∶(6÷2)
a∶b=4∶3。
熟练掌握比例的基本性质是解答本题的关键。
15.
【分析】根据倒数的意义:乘积是1的两个数互为倒数;比例的基本性质:两个外项之积等于两个内项之积;把0.6化成分数,即可解答。
【详解】0.6=
1÷
=1×
=
利用倒数的意义,比例的基本性质进行解答。
16.2.5
【分析】根据图上距离÷比例尺=实际距离,进行换算即可。
【详解】5厘米=50毫米
50÷20=2.5(毫米)
关键是理解比例尺的意义,掌握图上距离与实际距离的换算方法。
17.×
【分析】根据比例尺的意义:比例尺=图上距离∶实际距离,代入数据,即可解答。
【详解】240m=24000cm
6∶24000
=(6÷6)∶(24000÷6)
=1∶4000
学校操场的实际长是240m,画在图纸上的长是6cm。这张图纸的比例尺是1∶4000。
故答案为:×
利用比例尺的意义进行解答;注意单位名数的统一。
18.×
【分析】根据比例的基本性质:比例的两个内项之积等于两个外项之积,据此解答。
【详解】∶和∶2
×2=
×=
≠,所以∶和∶2不能组成比例。
原题干说法错误。
故答案为:×
熟练掌握比例的基本性质是解答本题的关键。
19.×
【分析】首先明确:10以内最大的质数是7,再结合比例的基本性质和倒数的意义解答即可。
【详解】因为两个内项互为倒数,所以两个内项的积是1,两个外项的积是1。
10以内最大的质数是7,因为7的倒数是,所以另一个外项是。
故答案为:×
此题考查比例性质的应用:两个内项之积等于两个外项之积。
20.√
【分析】组成比例两端的两项叫做外项,中间的两项叫做内项,据此判断。
【详解】在比例中,3和是比例的外项,4.5和是比例的内项;所以原题说法正确。
故答案为:√
本题主要考查了比例的意义,解题的关键是熟记组成比例两端的两项叫做外项,中间的两项叫做内项。
21.×
【分析】根据倒数的意义,互为倒数的两个数乘积是1,两个外项互为倒数,那么它们的乘积是1。根据比例的基本性质,用两外项之积除以其中一个内项,可求出另一个内项。
【详解】由分析可知:
1÷=
所以另一个内项是 。
故答案为:×
本题考查了倒数的认识以及比例的基本性质,比例的两外项之积等于两内项之积。
22.√
【分析】根据数值比例尺的意义可知:一幅地图的比例尺是1∶5,表示图上1厘米代表实际距离5厘米。
【详解】5÷1=5
一幅地图的比例尺是1∶5,它表示实际距离是图上距离的5倍;此说法正确。
故答案为:√
本题主要考查学生对数值比例尺意义的理解。
23.×
【分析】在比例中,两内项积等于两外项积,据此判断。
【详解】因为4a=5b,可把4和a看作比例的外项,5和b看作比例的内项,所以4∶5=b∶a。原题说法错误。
故答案为:×
此题考查了比例的基本性质,要学会灵活运用。
24.27;4;;0.5;
40;;25.52;0.01。
【分析】根据小数、分数、百分数的加减乘除运算以及求比值的计算方法解答。
【详解】8.1÷0.3=27 32×12.5%=4 0.8∶2.4= 0.3+=0.5
44÷=40 ×= 8=25.52 0.1=0.01
考查了四则运算,关键是熟练掌握计算法则正确进行计算。
25.x=2;x=8;x=5.6
【分析】(1)先把方程左边化简为3.8x,两边再同时除以3.8;
(2)根据比例的基本性质,把比例化为方程,两边再同时除以0.4;
(3)根据比例的基本性质,把比例化为方程,两边再同时乘7。
【详解】(1)5x-1.2x=7.6
解:3.8x=7.6
3.8x÷3.8=7.6÷3.8
x=2
(2)x∶80%=4∶0.4
解:0.4x=3.2
0.4x÷0.4=3.2÷0.4
x=8
(3)x∶6.4=∶
解:x×=6.4×
x=0.8
7×x=0.8×7
x=5.6
26.x=24;x=3;y=20
【分析】(1)方程两边先同时减去9,然后两边同时除以。
(2)将比例式化成方程后两边同时除以2.4。
(3)先化简2y-30%y,然后方程的两边同时除以(2-30%)的差。
【详解】(1)x+9=30
解:x+9-9=30-9
x=21
x÷=21÷
x=24
(2)8∶x=2.4∶0.9
解:2.4x=8×0.9
2.4x=7.2
2.4x÷2.4=7.2÷2.4
x=3
(3)2y-30%y=34
解:2y-0.3y=34
1.7y=34
1.7y÷1.7=34÷1.7
y=20
27.(1)1∶30000
(2)东,北60;1200
(3)见详解
【分析】(1)用尺子测量,即可知道学校到街心花园的距离是3厘米,实际距离是900米,根据比例尺的公式:比例尺=图上距离∶实际距离,把数代入公式即可求解,要注意统一单位。
(2)根据地图上的方向(上北下南,左西右东),即可找出足球场在街心花园的方向,之后量出街心花园到足球场的图上距离,再根据公式:实际距离=图上距离÷比例尺,求出实际距离。
(3)图上距离=实际距离×比例尺,求出图上距离,再根据地图上的方向(上北下南,左西右东),即可找出游泳馆的位置。
【详解】(1)900米=90000厘米
3厘米∶90000厘米
=(3÷3)∶(90000÷3)
=1∶30000
所以这幅图的比例尺是:1∶30000
(2)足球场在街心花园图上距离4厘米处
4×30000=120000(厘米)
120000厘米=1200米
即足球场在街心花园的北偏东60°方向1200米。
(3)600米=60000厘米
60000×=2(厘米)
如下图所示:
本题主要学会找准方向,并熟练掌握图上距离和实际距离的关系是解题的关键。
28.2400平方米
【分析】根据:图上距离÷比例尺=实际距离,代入数据计算出平行四边形菜地实际的底和高,再应用平行四边形的面积公式,计算出菜地的实际面积。
【详解】3÷=3×2000=6000(厘米)=60(米)
2÷=2×2000=4000(厘米)=40(米)
60×40=2400(平方米)
答:这块菜地的实际面积是2400平方米。
理解比例尺的意义,结合平行四边形的特点,运用比例尺解决生活中的实际问题。
29.0.46小时
【分析】根据实际距离=图上距离÷比例尺,据此求出深圳光明城站到广州南站的实际距离,再利用公式:路程=时间×速度,可以求出G6258动车从光明城运行到广州南站大约需要的时间。
【详解】深圳光明城站到广州南站的实际距离为:
5÷=5×2000000=10000000(厘米)
10000000厘米=100千米
100÷217≈0.46(小时)
答:G6258动车从光明城运行到广州南站大约需要0.46小时。
此题主要考查了图上距离和实际距离之间的换算,同时也要能熟练应用路程公式。
30.150米;24米;1800平方米
【分析】根据实际距离=图上距离÷比例尺,代入数据算出这块三角形草地底和高的实际长度,再根据三角形的面积=底×高÷2计算面积即可。
【详解】三角形草地底的实际长度为:
2.5÷=15000(厘米)
15000厘米=150米
三角形草地高的实际长度为:
0.4÷=2400(厘米)
2400厘米=24米
三角形草地实际面积为:
150×24÷2
=3600÷2
=1800(平方米)
答:这块三角形草地的实际底是150米,高是24米;这块三角形草地的实际面积是1800平方米。
解答此题的关键是掌握比例尺=图上距离÷实际距离这个公式及其变形,同时要会灵活应用三角形的面积公式。
31.(1)逆;90
(2)、(3)、(4)见详解
【分析】(1)根据旋转的特征可知,图形①绕点M按逆时针旋转90°得到图形②。
(2)根据平移的特征,将图形②的3个顶点先向左平移6格,再向下平移2格,然后连接即可。
(3)根据轴对称图形的画法,以虚线a为对称轴,在对称轴的另一边画出与图形③的关键点,然后画出轴对称的图形。
(4)根据图形缩小知识,将图形①的底和高缩小至原来的二分之一,即缩小后的三角形底是6÷2=3(格),高是4÷2=2(格),形状不变,据此画图即可。
【详解】(1)图形①绕点按逆时针旋转90得到图形②。
(2)、(3)、(4)根据要求,作图如下:
本题考查了旋转、平移、图形的缩小等知识,掌握图形旋转、平移和缩小的特征是解答本题的关键。
32.24名
【分析】根据原来女性占总人数的分率,求出女性和男性的人数,再设后来来了x名女性,根据女性和男性人数比,列比例求解。
【详解】原来女性人数:216×=48(名)
男性人数:216-48=168(名)
解:设后来来了x名女性。
(48+x)∶168=3∶7
7×(48+x)=3×168
336+7x=504
336+7x-336=504-336
7x=168
7x÷7=168÷7
x=24
答:后来又来了24名女性志愿者。
本题主要考查比例的应用,关键注意男性志愿者的人数没有改变。
33.(1)长24米,宽20米,深4米
(2)832平方米
【分析】(1)图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可分别求出水池的长、宽、深的实际长度;
(2)贴瓷砖的面积,就是用表面积减去上口的面积,利用长方体表面积公式即可求解。
【详解】(1)水池实际的长:12÷=2400(厘米)=24(米)
水池实际的宽:10÷=2000(厘米)=20(米)
水池实际的深度:2÷=400(厘米)=4(米)
答:这个水池的长应挖24米、宽应挖20米、深应挖4米。
(2)(24×20+20×4+4×24)×2-24×20
=(480+80+96)×2-480
=656×2-480
=1312-480
=832(平方米)
答:这个水池的四周和底面要贴上瓷砖,贴瓷砖的实际面积是832平方米。
此题主要考查图上距离、实际距离和比例尺的关系,以及长方体的表面积公式的运用。
