6.2 用二叉树排序——树与二叉树 课件(共37张PPT)2022—2023学年教科版(2019)高中信息技术选择性必修1
文档属性
| 名称 | 6.2 用二叉树排序——树与二叉树 课件(共37张PPT)2022—2023学年教科版(2019)高中信息技术选择性必修1 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 信息科技(信息技术) | ||
| 更新时间 | 2023-02-07 07:13:22 | ||
图片预览





文档简介
树与二叉树
A
B
C
D
E
G
H
F
I
树
树是一种重要的非线性数据结构,直观的看,它是数据元素(在树中称之为节点)按分支关系组织起来的结构,与自然界的树很像。
树
日常生活中很多事物可以用树形图来表示,如家族族谱、动物分类等,如图所示
树
日常生活中很多事物可以用树形图来表示,如家族族谱、动物分类等,如图所示
树的基本概念
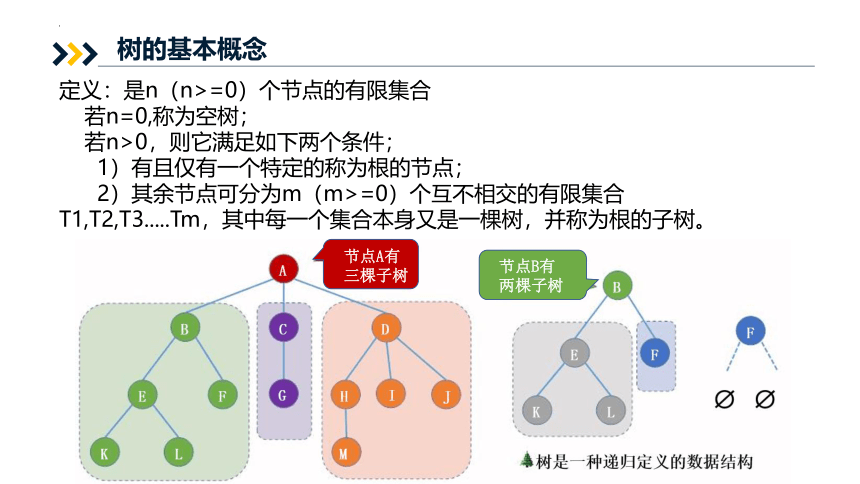
定义:是n(n>=0)个节点的有限集合
若n=0,称为空树;
若n>0,则它满足如下两个条件;
1)有且仅有一个特定的称为根的节点;
2)其余节点可分为m(m>=0)个互不相交的有限集合T1,T2,T3.....Tm,其中每一个集合本身又是一棵树,并称为根的子树。
节点A有三棵子树
节点B有两棵子树
树的基本术语
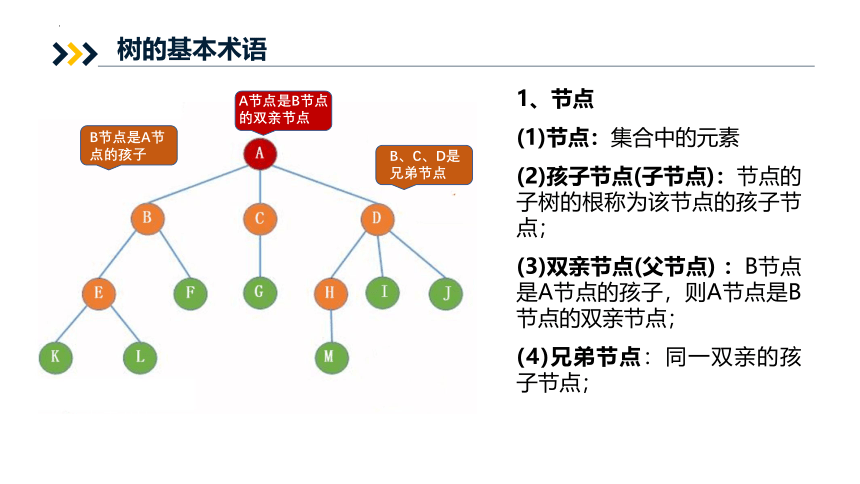
A节点是B节点的双亲节点
B节点是A节点的孩子
叶子节点
B、C、D是兄弟节点
1、节点
(1)节点:集合中的元素
(2)孩子节点(子节点):节点的子树的根称为该节点的孩子节点;
(3)双亲节点(父节点) :B节点是A节点的孩子,则A节点是B节点的双亲节点;
(4)兄弟节点:同一双亲的孩子节点;
树的基本术语
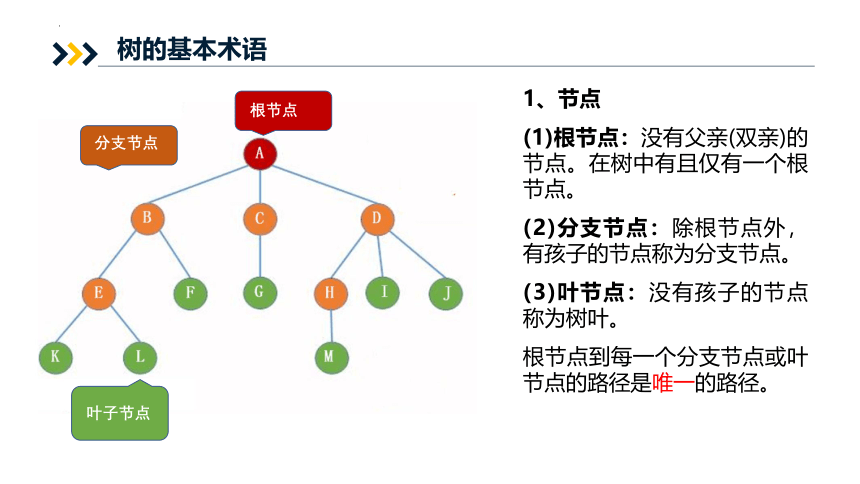
根节点
分支节点
叶子节点
1、节点
(1)根节点:没有父亲(双亲)的节点。在树中有且仅有一个根节点。
(2)分支节点:除根节点外,有孩子的节点称为分支节点。
(3)叶节点:没有孩子的节点称为树叶。
根节点到每一个分支节点或叶节点的路径是唯一的路径。
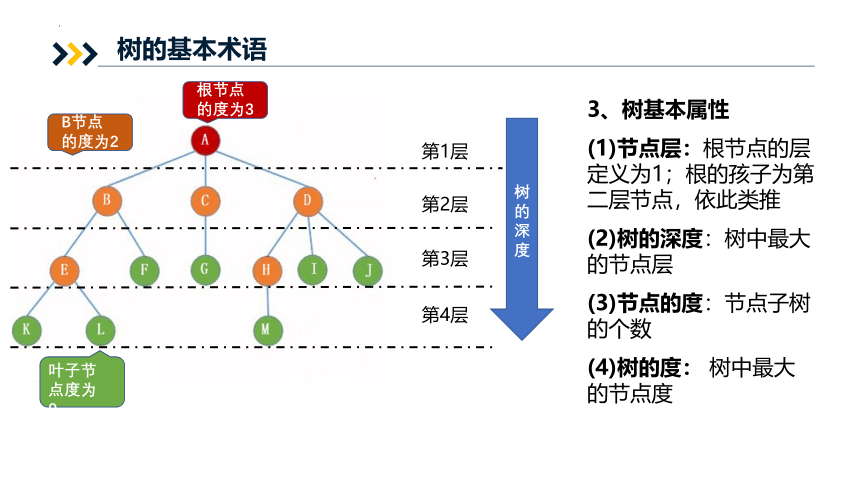
根节点的度为3
B节点的度为2
叶子节点度为0
树的基本术语
3、树基本属性
(1)节点层:根节点的层定义为1;根的孩子为第二层节点,依此类推
(2)树的深度:树中最大的节点层
(3)节点的度:节点子树的个数
(4)树的度: 树中最大的节点度
第1层
第2层
第3层
第4层
树的深度
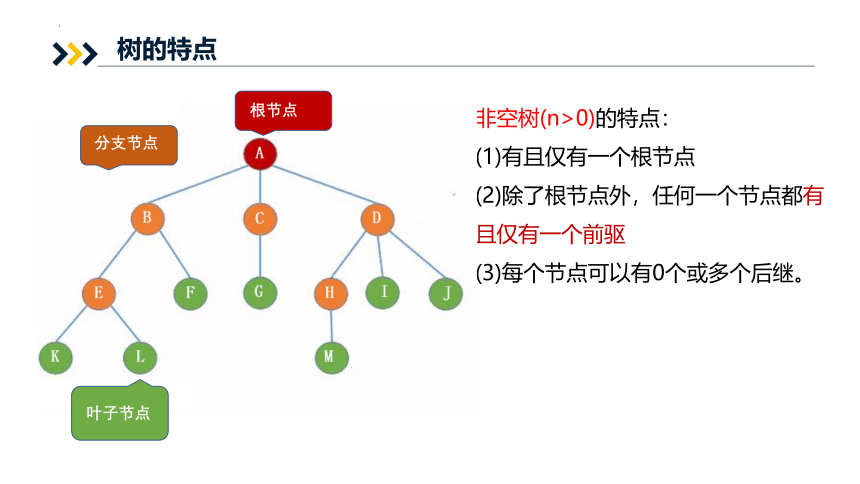
树的特点
非空树(n>0)的特点:
(1)有且仅有一个根节点
(2)除了根节点外,任何一个节点都有且仅有一个前驱
(3)每个节点可以有0个或多个后继。
根节点
分支节点
叶子节点
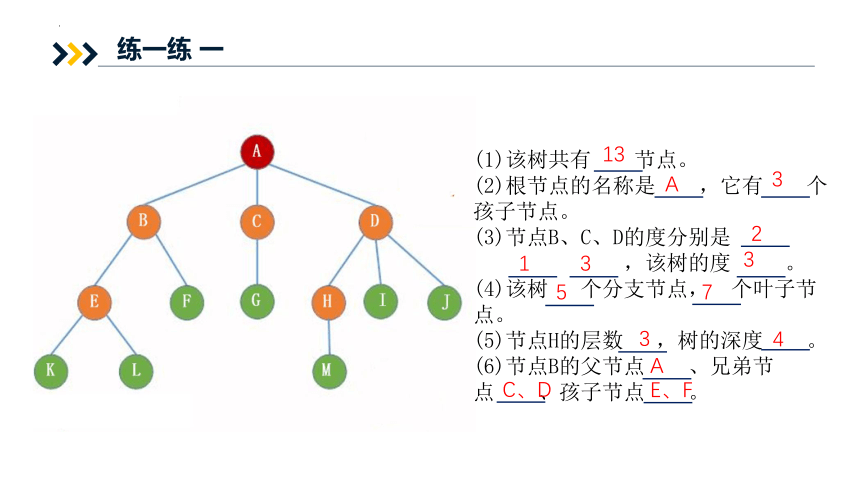
练一练 一
(1)该树共有 节点。
(2)根节点的名称是 ,它有 个孩子节点。
(3)节点B、C、D的度分别是
,该树的度 。
(4)该树 个分支节点, 个叶子节点。
(5)节点H的层数 ,树的深度 。
(6)节点B的父节点 、兄弟节点 、孩子节点 。
13
3
2
1
3
3
5
7
3
4
A
C、D
E、F
A
二叉树
二叉树是n(n≥0)个节点的有限集合:
① n = 0时,二叉树是一棵空树。。
② 当n ≠ 0时,二叉树是由一个根节点(N)和两个互不相交的集合被称为根的左子树(L)和右子树(R)组成。左子树和右子树又分别是一棵二叉树。
二叉树的基本概念
节点A的右子树
①每个节点至多只有两棵子树。
②左右子树不能颠倒
二叉树的特点
节点A的右子树
二叉树的五种基本形态
(a)
空二叉树
A
A
B
(c)
根和左子树
A
(b)
根和空二叉树
A
C
(d)
根和右子树
A
C
B
(e)
根和左右子树
①二叉树第i层至多有2i?1个节点(i≥1)
?
二叉树的性质
应用:
(1)如图所示,
第1层上最多只有 个节点;
第2层上最多只有 个节点,以此类推,
第i层上最多只有 个节点。
1
2
2i?1
?
②深度为k的二叉树多有2k?1个节点(i≥1)
?
二叉树的性质
应用:
根据性质①可知,第1层节点数最多为20。第2层节点数最多为21,以此类推,深度为k的二叉树节点最多有20+21+22+……+2k=2k-1
(2)某二叉树深度为4,则该二叉树最多有 个节点。
15
③在任意一棵二叉树中,若度为2的节点数量为n2 ,叶子节点数为n0,则n0=n2+1(叶子节点比分支节点多一个)
二叉树的性质
应用:
如图甲,度为2的节点数为5,叶子节点数为6;
如图乙:度为2的节点数为 ,叶子节点数为 。
图甲
图乙
5
6
特点:①每个节点的度为2(具有两个非空子树),或者度数为0(叶子节点)
②所有叶子节点都在同一层
特殊都二叉树——满二叉树
应用:
根据二叉树性质可知:
(1)满二叉树第k层上的节点数一定为 。
(2)一个深度为k的满二叉树一定有 个节点。
2k-1
2k-1
特殊都二叉树——满二叉树
特点:①至多只有最下两层中的节点的度小于2
②最下一层的叶子节点都依次排列在该层最左边位置
特殊都二叉树——完全二叉树
应用:
根据二叉树性质可知:
(1)一棵深度为k的完全二叉树,第k-1层的节点个数为 。第k层的节点数 (填关系运算符) 2k-1 。
(2)已知某完全二叉树有200个节点,
则该二叉树的高度为 。
2k-2
<=
8
特殊都二叉树——完全二叉树
20+21+22+23+24+25+26=127
27=128
满二叉树
完全二叉树
完全二叉树
非完全二叉树
非完全二叉树
练一练 二
对二叉树各个节点进行访问,即是遍历操作。
1、前序遍历(根 左 右)
先访问根节点,再访问左子树,最后访问右子树。
如右图的前序遍历顺序为:
A-B-C
2
二叉树的基本遍历
1
A
B
C
2、中序遍历(左 根 右)
先访问左子树,再访问根节点,最后访问右子树。
如右图的中序遍历顺序为:
B-A-C
二叉树的基本遍历
1
2
A
B
C
3、后序遍历(左 右 根)
先访问左子树,再访问右子树,最后访问根节点。
如右图的后序遍历顺序为:
B-C-A
二叉树的基本遍历
1
2
A
B
C
练一练 三
A
B
C
E
G
F
D
A
B
C
E
G
K
F
I
J
D
H
1、
2、
请写出下面两道题的前序遍历、中序遍历、后序遍历。
练一练 三
A-B-D-E-C-F-G
1、前序遍历(根 左 右)
A
B
C
E
G
F
D
1
2
4
5
3
6
练一练 三
D-B-E-A-F-C-G
1、中序遍历(左 根 右)
A
B
C
E
G
F
D
1
2
3
4
5
6
练一练 三
D-E-B-F-G-C-A
1、后序遍历(左 右 根)
A
B
C
E
G
F
D
1
2
3
5
4
6
2、前序遍历(根 左 右)
A-B-D-H-E-C-F-I-G-J-K
A
B
C
E
G
K
F
I
J
D
H
1
2
3
4
5
6
7
8
9
10
练一练 三
2、中序遍历(左 根 右)
D-H-B-E-A-I-F-C-J-G-K
A
B
C
E
G
K
F
I
J
D
H
1
2
3
4
5
6
8
9
10
7
练一练 三
2、后序遍历(左 右 根)
H-D-E-B-I-F-J-K-G-C-A
A
B
C
E
G
K
F
I
J
D
H
1
2
3
4
5
7
8
9
6
10
练一练 三
表达式树
树结构表示算数表达式:
内部节点来表示运算符,
叶子节点来表示运算数。
例如 3-1
—
1
3
T
如何构建3-1的树结构T:
1)创建一棵树“T”,树根是“-”
2)为T插入左边的子节点,内容是“3”
3)为T插入右边的子节点,内容是“1”
表达式树
复杂一些的算数表达式 5+(3-1)
—
1
3
T
如何构建5+(3-1)的树结构T:
1)创建一棵树“T”,树根是
2)为T插入左边的子节点,内容是
3)为T插入右边的子节点,内容是
右子节点记为R
4)为R插入左边的子节点,内容是
5)为R插入右边的子节点,内容是
+
5
“+”
“5”
“-”
“3”
“1”
R
表达式树
—
1
3
T
+
5
R
后序遍历序列:531-+
四则运算表达式的逆波兰表示(后缀表达式)
中序遍历序列:5+(3-1)
四则运算表达式 中缀表达式
前序遍历序列:+5-3 1
四则运算表达式的波兰表示(前缀表达式)
如果对这棵树进行遍历
如何构建(3+4)*(9-6)
的树结构T:
1)创建一棵树“T”,树根是“*”
2)为T插入左边的子节点,内容是“+”右子节点记为L
4)为L插入左边的子节点,内容是“3”
5)为L插入右边的子节点,内容是“4”
3)为T插入右边的子节点,内容是“-”
右子节点记为R
4)为R插入左边的子节点,内容是“9”
5)为R插入右边的子节点,内容是“6”
练一练 四
画出下面表达式的树结构,并写出创建过程。
(3+4)*(9-6)
—
6
9
T
*
R
+
4
3
L
A
B
C
D
E
G
H
F
I
树
树是一种重要的非线性数据结构,直观的看,它是数据元素(在树中称之为节点)按分支关系组织起来的结构,与自然界的树很像。
树
日常生活中很多事物可以用树形图来表示,如家族族谱、动物分类等,如图所示
树
日常生活中很多事物可以用树形图来表示,如家族族谱、动物分类等,如图所示
树的基本概念
定义:是n(n>=0)个节点的有限集合
若n=0,称为空树;
若n>0,则它满足如下两个条件;
1)有且仅有一个特定的称为根的节点;
2)其余节点可分为m(m>=0)个互不相交的有限集合T1,T2,T3.....Tm,其中每一个集合本身又是一棵树,并称为根的子树。
节点A有三棵子树
节点B有两棵子树
树的基本术语
A节点是B节点的双亲节点
B节点是A节点的孩子
叶子节点
B、C、D是兄弟节点
1、节点
(1)节点:集合中的元素
(2)孩子节点(子节点):节点的子树的根称为该节点的孩子节点;
(3)双亲节点(父节点) :B节点是A节点的孩子,则A节点是B节点的双亲节点;
(4)兄弟节点:同一双亲的孩子节点;
树的基本术语
根节点
分支节点
叶子节点
1、节点
(1)根节点:没有父亲(双亲)的节点。在树中有且仅有一个根节点。
(2)分支节点:除根节点外,有孩子的节点称为分支节点。
(3)叶节点:没有孩子的节点称为树叶。
根节点到每一个分支节点或叶节点的路径是唯一的路径。
根节点的度为3
B节点的度为2
叶子节点度为0
树的基本术语
3、树基本属性
(1)节点层:根节点的层定义为1;根的孩子为第二层节点,依此类推
(2)树的深度:树中最大的节点层
(3)节点的度:节点子树的个数
(4)树的度: 树中最大的节点度
第1层
第2层
第3层
第4层
树的深度
树的特点
非空树(n>0)的特点:
(1)有且仅有一个根节点
(2)除了根节点外,任何一个节点都有且仅有一个前驱
(3)每个节点可以有0个或多个后继。
根节点
分支节点
叶子节点
练一练 一
(1)该树共有 节点。
(2)根节点的名称是 ,它有 个孩子节点。
(3)节点B、C、D的度分别是
,该树的度 。
(4)该树 个分支节点, 个叶子节点。
(5)节点H的层数 ,树的深度 。
(6)节点B的父节点 、兄弟节点 、孩子节点 。
13
3
2
1
3
3
5
7
3
4
A
C、D
E、F
A
二叉树
二叉树是n(n≥0)个节点的有限集合:
① n = 0时,二叉树是一棵空树。。
② 当n ≠ 0时,二叉树是由一个根节点(N)和两个互不相交的集合被称为根的左子树(L)和右子树(R)组成。左子树和右子树又分别是一棵二叉树。
二叉树的基本概念
节点A的右子树
①每个节点至多只有两棵子树。
②左右子树不能颠倒
二叉树的特点
节点A的右子树
二叉树的五种基本形态
(a)
空二叉树
A
A
B
(c)
根和左子树
A
(b)
根和空二叉树
A
C
(d)
根和右子树
A
C
B
(e)
根和左右子树
①二叉树第i层至多有2i?1个节点(i≥1)
?
二叉树的性质
应用:
(1)如图所示,
第1层上最多只有 个节点;
第2层上最多只有 个节点,以此类推,
第i层上最多只有 个节点。
1
2
2i?1
?
②深度为k的二叉树多有2k?1个节点(i≥1)
?
二叉树的性质
应用:
根据性质①可知,第1层节点数最多为20。第2层节点数最多为21,以此类推,深度为k的二叉树节点最多有20+21+22+……+2k=2k-1
(2)某二叉树深度为4,则该二叉树最多有 个节点。
15
③在任意一棵二叉树中,若度为2的节点数量为n2 ,叶子节点数为n0,则n0=n2+1(叶子节点比分支节点多一个)
二叉树的性质
应用:
如图甲,度为2的节点数为5,叶子节点数为6;
如图乙:度为2的节点数为 ,叶子节点数为 。
图甲
图乙
5
6
特点:①每个节点的度为2(具有两个非空子树),或者度数为0(叶子节点)
②所有叶子节点都在同一层
特殊都二叉树——满二叉树
应用:
根据二叉树性质可知:
(1)满二叉树第k层上的节点数一定为 。
(2)一个深度为k的满二叉树一定有 个节点。
2k-1
2k-1
特殊都二叉树——满二叉树
特点:①至多只有最下两层中的节点的度小于2
②最下一层的叶子节点都依次排列在该层最左边位置
特殊都二叉树——完全二叉树
应用:
根据二叉树性质可知:
(1)一棵深度为k的完全二叉树,第k-1层的节点个数为 。第k层的节点数 (填关系运算符) 2k-1 。
(2)已知某完全二叉树有200个节点,
则该二叉树的高度为 。
2k-2
<=
8
特殊都二叉树——完全二叉树
20+21+22+23+24+25+26=127
27=128
满二叉树
完全二叉树
完全二叉树
非完全二叉树
非完全二叉树
练一练 二
对二叉树各个节点进行访问,即是遍历操作。
1、前序遍历(根 左 右)
先访问根节点,再访问左子树,最后访问右子树。
如右图的前序遍历顺序为:
A-B-C
2
二叉树的基本遍历
1
A
B
C
2、中序遍历(左 根 右)
先访问左子树,再访问根节点,最后访问右子树。
如右图的中序遍历顺序为:
B-A-C
二叉树的基本遍历
1
2
A
B
C
3、后序遍历(左 右 根)
先访问左子树,再访问右子树,最后访问根节点。
如右图的后序遍历顺序为:
B-C-A
二叉树的基本遍历
1
2
A
B
C
练一练 三
A
B
C
E
G
F
D
A
B
C
E
G
K
F
I
J
D
H
1、
2、
请写出下面两道题的前序遍历、中序遍历、后序遍历。
练一练 三
A-B-D-E-C-F-G
1、前序遍历(根 左 右)
A
B
C
E
G
F
D
1
2
4
5
3
6
练一练 三
D-B-E-A-F-C-G
1、中序遍历(左 根 右)
A
B
C
E
G
F
D
1
2
3
4
5
6
练一练 三
D-E-B-F-G-C-A
1、后序遍历(左 右 根)
A
B
C
E
G
F
D
1
2
3
5
4
6
2、前序遍历(根 左 右)
A-B-D-H-E-C-F-I-G-J-K
A
B
C
E
G
K
F
I
J
D
H
1
2
3
4
5
6
7
8
9
10
练一练 三
2、中序遍历(左 根 右)
D-H-B-E-A-I-F-C-J-G-K
A
B
C
E
G
K
F
I
J
D
H
1
2
3
4
5
6
8
9
10
7
练一练 三
2、后序遍历(左 右 根)
H-D-E-B-I-F-J-K-G-C-A
A
B
C
E
G
K
F
I
J
D
H
1
2
3
4
5
7
8
9
6
10
练一练 三
表达式树
树结构表示算数表达式:
内部节点来表示运算符,
叶子节点来表示运算数。
例如 3-1
—
1
3
T
如何构建3-1的树结构T:
1)创建一棵树“T”,树根是“-”
2)为T插入左边的子节点,内容是“3”
3)为T插入右边的子节点,内容是“1”
表达式树
复杂一些的算数表达式 5+(3-1)
—
1
3
T
如何构建5+(3-1)的树结构T:
1)创建一棵树“T”,树根是
2)为T插入左边的子节点,内容是
3)为T插入右边的子节点,内容是
右子节点记为R
4)为R插入左边的子节点,内容是
5)为R插入右边的子节点,内容是
+
5
“+”
“5”
“-”
“3”
“1”
R
表达式树
—
1
3
T
+
5
R
后序遍历序列:531-+
四则运算表达式的逆波兰表示(后缀表达式)
中序遍历序列:5+(3-1)
四则运算表达式 中缀表达式
前序遍历序列:+5-3 1
四则运算表达式的波兰表示(前缀表达式)
如果对这棵树进行遍历
如何构建(3+4)*(9-6)
的树结构T:
1)创建一棵树“T”,树根是“*”
2)为T插入左边的子节点,内容是“+”右子节点记为L
4)为L插入左边的子节点,内容是“3”
5)为L插入右边的子节点,内容是“4”
3)为T插入右边的子节点,内容是“-”
右子节点记为R
4)为R插入左边的子节点,内容是“9”
5)为R插入右边的子节点,内容是“6”
练一练 四
画出下面表达式的树结构,并写出创建过程。
(3+4)*(9-6)
—
6
9
T
*
R
+
4
3
L
