第八章 浮力综合计算的常见类型课件(共24张PPT)
文档属性
| 名称 | 第八章 浮力综合计算的常见类型课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 474.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-08 10:07:04 | ||
图片预览






文档简介
第八章 压强与浮力
浮力综合计算的常见类型
一、压力差法:F浮 =F下表面 — F上表面 (浮力方向:竖直向上)
1.某物块浸没在水中时,下表面受到水的压力为2.3N,上表面受到水的压力为1.5N,则该物块受到水的浮力为________N,方向为________。
2.在图中,浸没在液体中的物体,两个相对的侧面所受液体的_________相互平衡,对物体水平方向的受力没有影响。其上、下表面受到液体对它的压力不同,这就是浮力产生的原因。如果F1=8 N,物体受到的浮力是4 N,则F2=______N。
二、称重法:F浮 =G(空气中的示数) — F液示
1.重14.7牛的石块挂在弹簧秤下端,将它完全没入水中,这时弹簧秤示数是9.8牛,则石块受到的浮力大小是 牛,石块排开水的体积是 m3 ,石块的体积是 m3 .
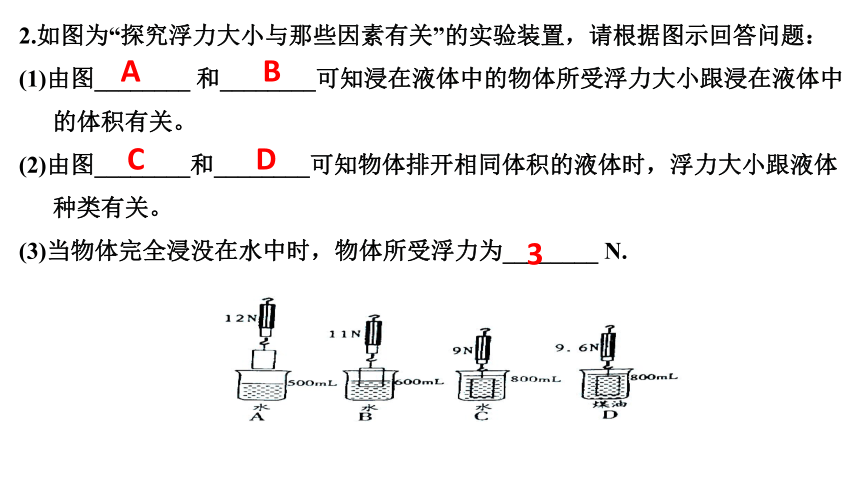
2.如图为“探究浮力大小与那些因素有关”的实验装置,请根据图示回答问题:
(1)由图________ 和________可知浸在液体中的物体所受浮力大小跟浸在液体中的体积有关。
(2)由图________和________可知物体排开相同体积的液体时,浮力大小跟液体种类有关。
(3)当物体完全浸没在水中时,物体所受浮力为________ N.
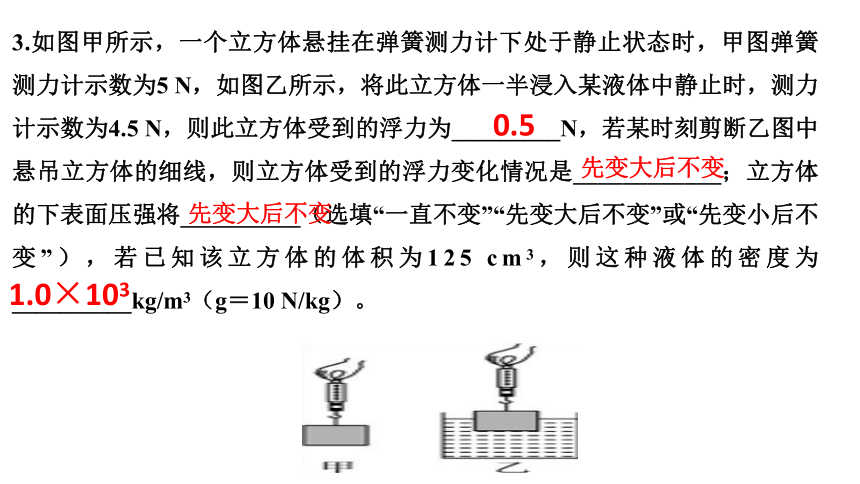
3.如图甲所示,一个立方体悬挂在弹簧测力计下处于静止状态时,甲图弹簧测力计示数为5 N,如图乙所示,将此立方体一半浸入某液体中静止时,测力计示数为4.5 N,则此立方体受到的浮力为_________N,若某时刻剪断乙图中悬吊立方体的细线,则立方体受到的浮力变化情况是____________;立方体的下表面压强将__________(选填“一直不变”“先变大后不变”或“先变小后不变”),若已知该立方体的体积为125 cm3,则这种液体的密度为__________kg/m3(g=10 N/kg)。
4.用弹簧测力计悬挂一实心物块,物块下表面与水面刚好接触,如图甲所示。从此处匀速下放物块,直至浸没于水中并继续匀速下放(物块未与水底接触)。物块下放过程中,弹簧测力计示数F与物块下表面浸入水的深度h的关系如图乙。(g取10 N/kg,水的密度是1.0×103 kg/m)求:
(1)物块受到的重力;
(2)物块完全浸没在水中受到的浮力;
(3)物块的密度。
(1)物块受到的重力(2)物块完全浸没在水中受到的浮力;
解:由题可知,实心物块的重力G=18 N,浸没在液体中时,圆柱体受到的拉力F=10 N,
实心物块受到的浮力F浮=G-F=18 N-10 N=8 N。
(3)物块的密度
解:因为物体浸没时的浮力为:F浮=8 N
由阿基米德原理可知,F浮=ρ液gV排,
三、阿基米德原理法:F浮=G排=m排g=ρ液gV排
1.在平静的池水中漂浮有一个木球,木球的体积为4 dm3,露出水面的体积为总体积的四分之一,那么木球受到的浮力为_______N。木球的密度为___________kg/m3。(g=10 N/kg)
2.一艘轮船在河里航行时的排水量是 吨,它受到的浮力为 牛.从河里开到海里,它受到的浮力 (填“变大”、“变小”或“不变”),由于河水密度 海水密度,(填“大于”、“小于”、“等于”)船从河里开到海里排开液体体积 。
3.创新小组自制简易“浸没式液体密度计”,过程为:
①将一实心小球悬挂在弹簧测力计下方,示数如图甲所示
②将小球浸没在水中,弹簧测力计示数如图乙所示;
③将小球浸没在某未知液体中,弹簧测力计示数如图丙所示。
已知ρ水=1×103 kg/m3,g取
10 N/kg,问:
(1)该小球的密度有多大?
解:由图甲可知:金属球的重力G=5 N,
则小球的质量
由图乙可知:弹簧测力计的示数为F1=4 N,小球在水中受到的浮力F浮1=G-F1=5 N-4 N=1 N。
由于小球处于浸没状态,则根据F浮=ρ液gV排可得:
(2)未知液体的密度有多大?
解:由图丙可知:弹簧测力计的示数F2=3 N,
小球在液体中受到的浮力F浮2=G-F2=5 N-3 N=2 N;
由于小球处于浸没状态,则根据F浮=ρ液gV排可得:
液体的密度
(3)该密度计的最大测量值是________kg/m3。
(4)在测量范围内,某待测液体的密度ρ与弹簧测力计示数F的关系式为________________,则该“浸没式液体密度计”的刻度值分布________(填“均匀”或“不均匀”)。
三、平衡法:悬浮或者漂浮条件 F浮=G物 (或ρ液=ρ物)
1.物块P与金属球Q用细线连接,一起放入装有一定质量水的柱状容器内,二者恰好悬浮,如图甲所示,此时柱状容器中水的深度为23 cm,物块P重1 N、体积为1.25×10-4m3(ρ水=1.0×103 kg/m3,g取10 N/kg)。
(1)求图甲中水对容器底部的压强;
解:图甲中水的深度h=23 cm=0.23 m,图甲中水对容器底部的压强
p=ρ水gh=1.0×103 kg/m3×10 N/kg×0.23 m=2.3×103 Pa。
(2)求图甲中物块P所受浮力的大小;
解:物块P浸没在水中,则物块P排开水的体积V排=V=1.25×10-4m3,由阿基米德原理可得图甲中物块P所受的浮力
F浮=ρ水gV排=1.0×103 kg/m3×10 N/kg×1.25×10-4m3=1.25 N。
(3)若剪断细线,物块P上浮,金属球Q下沉,待稳定后,物块P漂浮于水面,如图乙所示,求此时物块P露出水面的体积。
解:图乙中物块P漂浮于水面,由漂浮条件可知,此时物块P所受的浮力F浮′=G=1 N,
由F浮=ρ水gV排可得此时物块P排开水的体积
则物块P露出水面的体积
V露=V-V排′=1.25×10-4m3-1×10-4m3=2.5×10-5m3。
2.水平桌面上有一容器,底面积为100 cm2,容器底有一个质量为132 g、体积为120 cm3的小球,如图甲所示(ρ水=1.0×103 kg/m3,g取10 N/kg)。
(1)向容器中注入质量为1.6 kg的水时,水深13 cm,如图乙所示,求水对容器底的压强;
解:水深h=13 cm=0.13 m,水对容器底的压强
p=ρ水gh=1.0×103 kg/m3×10 N/kg×0.13 m=1 300 Pa。
(2)再向容器中慢慢加入适量盐并搅拌,直到小球悬浮为止,如图丙所示,求此时盐水的密度ρ1;
解:如题图丙所示,小球悬浮,
则此时盐水的密度
(3)继续向容器中加盐并搅拌,某时刻小球静止,将密度计放入盐水中,测得盐水的密度ρ2=1.2×103 kg/m3,求小球浸入盐水中的体积。
解:由于ρ2>ρ球,则小球在密度为ρ2的盐水中处于漂浮状态,
则F浮=G=mg=132×10-3 kg×10 N/kg=1.32 N,
根据F浮=ρ液gV排可得
浮力综合计算的常见类型
一、压力差法:F浮 =F下表面 — F上表面 (浮力方向:竖直向上)
1.某物块浸没在水中时,下表面受到水的压力为2.3N,上表面受到水的压力为1.5N,则该物块受到水的浮力为________N,方向为________。
2.在图中,浸没在液体中的物体,两个相对的侧面所受液体的_________相互平衡,对物体水平方向的受力没有影响。其上、下表面受到液体对它的压力不同,这就是浮力产生的原因。如果F1=8 N,物体受到的浮力是4 N,则F2=______N。
二、称重法:F浮 =G(空气中的示数) — F液示
1.重14.7牛的石块挂在弹簧秤下端,将它完全没入水中,这时弹簧秤示数是9.8牛,则石块受到的浮力大小是 牛,石块排开水的体积是 m3 ,石块的体积是 m3 .
2.如图为“探究浮力大小与那些因素有关”的实验装置,请根据图示回答问题:
(1)由图________ 和________可知浸在液体中的物体所受浮力大小跟浸在液体中的体积有关。
(2)由图________和________可知物体排开相同体积的液体时,浮力大小跟液体种类有关。
(3)当物体完全浸没在水中时,物体所受浮力为________ N.
3.如图甲所示,一个立方体悬挂在弹簧测力计下处于静止状态时,甲图弹簧测力计示数为5 N,如图乙所示,将此立方体一半浸入某液体中静止时,测力计示数为4.5 N,则此立方体受到的浮力为_________N,若某时刻剪断乙图中悬吊立方体的细线,则立方体受到的浮力变化情况是____________;立方体的下表面压强将__________(选填“一直不变”“先变大后不变”或“先变小后不变”),若已知该立方体的体积为125 cm3,则这种液体的密度为__________kg/m3(g=10 N/kg)。
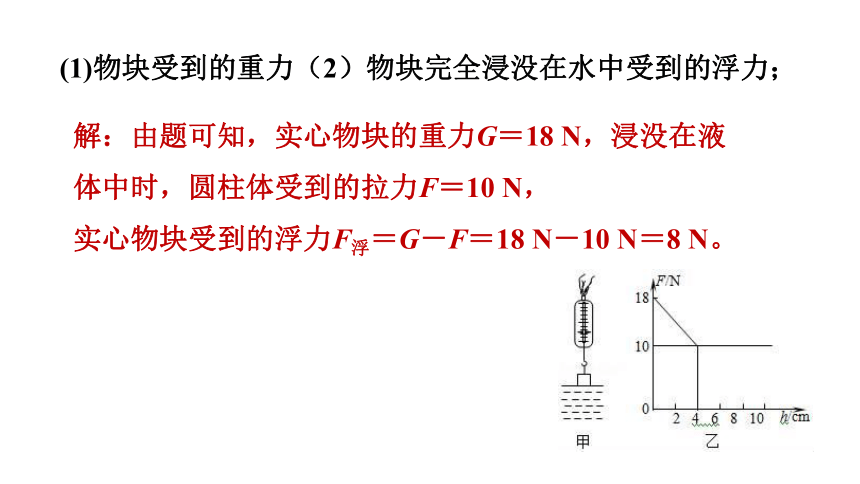
4.用弹簧测力计悬挂一实心物块,物块下表面与水面刚好接触,如图甲所示。从此处匀速下放物块,直至浸没于水中并继续匀速下放(物块未与水底接触)。物块下放过程中,弹簧测力计示数F与物块下表面浸入水的深度h的关系如图乙。(g取10 N/kg,水的密度是1.0×103 kg/m)求:
(1)物块受到的重力;
(2)物块完全浸没在水中受到的浮力;
(3)物块的密度。
(1)物块受到的重力(2)物块完全浸没在水中受到的浮力;
解:由题可知,实心物块的重力G=18 N,浸没在液体中时,圆柱体受到的拉力F=10 N,
实心物块受到的浮力F浮=G-F=18 N-10 N=8 N。
(3)物块的密度
解:因为物体浸没时的浮力为:F浮=8 N
由阿基米德原理可知,F浮=ρ液gV排,
三、阿基米德原理法:F浮=G排=m排g=ρ液gV排
1.在平静的池水中漂浮有一个木球,木球的体积为4 dm3,露出水面的体积为总体积的四分之一,那么木球受到的浮力为_______N。木球的密度为___________kg/m3。(g=10 N/kg)
2.一艘轮船在河里航行时的排水量是 吨,它受到的浮力为 牛.从河里开到海里,它受到的浮力 (填“变大”、“变小”或“不变”),由于河水密度 海水密度,(填“大于”、“小于”、“等于”)船从河里开到海里排开液体体积 。
3.创新小组自制简易“浸没式液体密度计”,过程为:
①将一实心小球悬挂在弹簧测力计下方,示数如图甲所示
②将小球浸没在水中,弹簧测力计示数如图乙所示;
③将小球浸没在某未知液体中,弹簧测力计示数如图丙所示。
已知ρ水=1×103 kg/m3,g取
10 N/kg,问:
(1)该小球的密度有多大?
解:由图甲可知:金属球的重力G=5 N,
则小球的质量
由图乙可知:弹簧测力计的示数为F1=4 N,小球在水中受到的浮力F浮1=G-F1=5 N-4 N=1 N。
由于小球处于浸没状态,则根据F浮=ρ液gV排可得:
(2)未知液体的密度有多大?
解:由图丙可知:弹簧测力计的示数F2=3 N,
小球在液体中受到的浮力F浮2=G-F2=5 N-3 N=2 N;
由于小球处于浸没状态,则根据F浮=ρ液gV排可得:
液体的密度
(3)该密度计的最大测量值是________kg/m3。
(4)在测量范围内,某待测液体的密度ρ与弹簧测力计示数F的关系式为________________,则该“浸没式液体密度计”的刻度值分布________(填“均匀”或“不均匀”)。
三、平衡法:悬浮或者漂浮条件 F浮=G物 (或ρ液=ρ物)
1.物块P与金属球Q用细线连接,一起放入装有一定质量水的柱状容器内,二者恰好悬浮,如图甲所示,此时柱状容器中水的深度为23 cm,物块P重1 N、体积为1.25×10-4m3(ρ水=1.0×103 kg/m3,g取10 N/kg)。
(1)求图甲中水对容器底部的压强;
解:图甲中水的深度h=23 cm=0.23 m,图甲中水对容器底部的压强
p=ρ水gh=1.0×103 kg/m3×10 N/kg×0.23 m=2.3×103 Pa。
(2)求图甲中物块P所受浮力的大小;
解:物块P浸没在水中,则物块P排开水的体积V排=V=1.25×10-4m3,由阿基米德原理可得图甲中物块P所受的浮力
F浮=ρ水gV排=1.0×103 kg/m3×10 N/kg×1.25×10-4m3=1.25 N。
(3)若剪断细线,物块P上浮,金属球Q下沉,待稳定后,物块P漂浮于水面,如图乙所示,求此时物块P露出水面的体积。
解:图乙中物块P漂浮于水面,由漂浮条件可知,此时物块P所受的浮力F浮′=G=1 N,
由F浮=ρ水gV排可得此时物块P排开水的体积
则物块P露出水面的体积
V露=V-V排′=1.25×10-4m3-1×10-4m3=2.5×10-5m3。
2.水平桌面上有一容器,底面积为100 cm2,容器底有一个质量为132 g、体积为120 cm3的小球,如图甲所示(ρ水=1.0×103 kg/m3,g取10 N/kg)。
(1)向容器中注入质量为1.6 kg的水时,水深13 cm,如图乙所示,求水对容器底的压强;
解:水深h=13 cm=0.13 m,水对容器底的压强
p=ρ水gh=1.0×103 kg/m3×10 N/kg×0.13 m=1 300 Pa。
(2)再向容器中慢慢加入适量盐并搅拌,直到小球悬浮为止,如图丙所示,求此时盐水的密度ρ1;
解:如题图丙所示,小球悬浮,
则此时盐水的密度
(3)继续向容器中加盐并搅拌,某时刻小球静止,将密度计放入盐水中,测得盐水的密度ρ2=1.2×103 kg/m3,求小球浸入盐水中的体积。
解:由于ρ2>ρ球,则小球在密度为ρ2的盐水中处于漂浮状态,
则F浮=G=mg=132×10-3 kg×10 N/kg=1.32 N,
根据F浮=ρ液gV排可得
