2022-2023学年湖南省益阳市桃江县三校联考九年级(上)期末数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年湖南省益阳市桃江县三校联考九年级(上)期末数学试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 720.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-07 09:04:19 | ||
图片预览




文档简介
2022-2023学年湖南省益阳市桃江县三校联考九年级(上)期末数学试卷
一、选择题(共12题,共48分)
1.(4分)已知函数y=(m+2)x是反比例函数,则m的值是( )
A.2 B.±2 C.±4 D.±6
2.(4分)如图,平行四边形ABCD的顶点B,D都在反比例函数y=(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形向左平移2个单位、再向下平移3个单位后点C的坐标为( )
A.(1,3) B.(4,3) C.(1,4) D.(2,4)
3.(4分)公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,则动力F(单位:N)关于动力臂l(单位:m)的函数解析式正确的是( )
A.F= B.F= C.F= D.F=
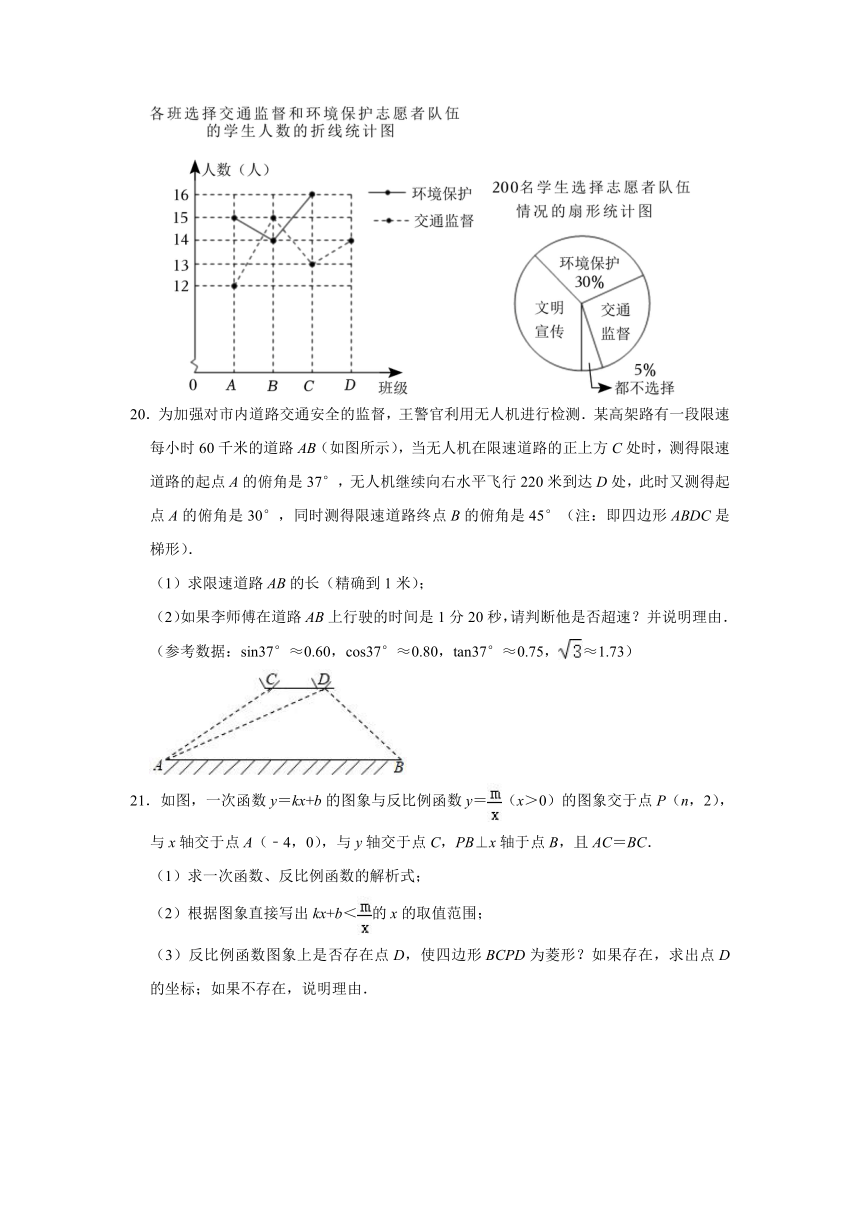
4.(4分)一个等腰三角形的底边长是6,腰长是一元二次方程x2﹣8x+15=0的一根,则此三角形的周长是( )
A.16 B.12 C.14 D.12或16
5.(4分)已知关于x的一元二次方程kx2﹣(2k﹣1)x+k﹣2=0有两个不相等的实数根,则实数k的取值范围是( )
A.k>﹣ B.k< C.k>﹣且k≠0 D.k<且k≠0
6.(4分)某商场销售一批衬衣,平均每天售出30件,每件衬衣盈利50元.为了增加盈利,尽快减少库存,商场决定采取降价措施.经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.若商场平均每天盈利2000元,则每件衬衣应降价( )
A.10元 B.15元 C.20元 D.25元
7.(4分)如图,已知AB∥CD∥EF,AC:AE=3:5,那么下列结论正确的是( )
A.BD:DF=2:3 B.AB:CD=2:3 C.CD:EF=3:5 D.DF:BF=2:5
8.(4分)如图,点E是线段BC的中点,∠B=∠C=∠AED,下列结论中,说法错误的是( )
A.△ABE与△ECD相似 B.△ABE与△AED相似
C. D.∠BAE=∠ADE
9.(4分)如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是( )
A.6米 B.8米 C.18米 D.24米
10.(4分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )
A.sinA= B.cosA= C.tanA= D.cosB=
11.(4分)一艘轮船在A处测得灯塔S在船的南偏东60°方向,轮船继续向正东航行30海里后到达B处,这时测得灯塔S在船的南偏西75°方向,则灯塔S离观测点A、B的距离分别是( )
A.(15﹣15)海里、15海里
B.(15﹣15)海里、5海里
C.(15﹣15)海里、15海里
D.(15﹣15)海里、15海里
12.(4分)如图,直线y=kx+b与双曲线交于点A(﹣8,1),B(2,﹣4),与两坐标轴分别交于点C,D,已知点E(1,0),连接AE,BE,作直线ED,将直线ED向上平移n(n>0)个单位长度后,与双曲线有唯一交点,则n的值为( )
A. B. C. D.
二、填空题(共5题,共20分)
13.(3分)某校来自甲、乙、丙、丁四个社区的学生人数分布如图,若来自甲社区的学生有120人,则该校学生总数为 人.
14.(3分)你吃过兰州拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(cm)是面条粗细(横截面积)x(cm2)的反比例函数,假设其图象如图所示,则y与x的函数关系式为 .
15.(3分)如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若Rt△ABC是“好玩三角形”,且∠A=90°,则tan∠ABC= .
16.(3分)在Rt△ABC中,∠ACB=90°,AC=3,BC=5,点D是斜边AB上一点(AD>BD)如果将△BCD沿CD所在直线翻折,点B落在点E处,连接AE,当AE⊥AC时,那么的值为 .
17.(3分)有A,B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字0,1,2,3;B布袋中有三个除标号外完全相同的小球,小球上分别标有数字0,1,2.小明先从A布袋中随机取出一个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.若用(m,n)表示小明取球时m与n的对应值,则使关于x的一元二次方程有实数根的概率为 .
三、解答题(共4题,共52分)
18.已知关于x的一元二次方程:x2+(k﹣5)x+4﹣k=0
(1)求证:无论k为何值,方程总有实数根;
(2)若方程的一个根是2,求另一个根及k的值.
19.某校积极开展中学生社会实践活动,决定成立文明宣传、环境保护、交通监督三个志愿者队伍,每名学生最多选择一个队伍.为了了解学生的选择意向,随机抽取A,B,C,D四个班,共200名学生进行调查.将调查得到的数据进行整理,绘制成如下统计图.
(1)求扇形统计图中交通监督所在扇形的圆心角度数;
(2)求D班选择环境保护的学生人数,并补全折线统计图;
(3)若该校共有学生2500人,试估计该校选择文明宣传的学生人数.
20.为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时60千米的道路AB(如图所示),当无人机在限速道路的正上方C处时,测得限速道路的起点A的俯角是37°,无人机继续向右水平飞行220米到达D处,此时又测得起点A的俯角是30°,同时测得限速道路终点B的俯角是45°(注:即四边形ABDC是梯形).
(1)求限速道路AB的长(精确到1米);
(2)如果李师傅在道路AB上行驶的时间是1分20秒,请判断他是否超速?并说明理由.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73)
21.如图,一次函数y=kx+b的图象与反比例函数y=(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)根据图象直接写出kx+b<的x的取值范围;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
2022-2023学年湖南省益阳市桃江县三校联考九年级(上)期末数学试卷
参考答案与试题解析
一、选择题(共12题,共48分)
1.(4分)已知函数y=(m+2)x是反比例函数,则m的值是( )
A.2 B.±2 C.±4 D.±6
【分析】根据反比例函数的定义得到m2﹣5=﹣1,且m+2≠0,由此求得m的值.
【解答】解:依题意得:m2﹣5=﹣1,且m+2≠0,
解得m=2.
故选:A.
2.(4分)如图,平行四边形ABCD的顶点B,D都在反比例函数y=(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形向左平移2个单位、再向下平移3个单位后点C的坐标为( )
A.(1,3) B.(4,3) C.(1,4) D.(2,4)
【分析】由平行四边形ABCD的顶点B,D都在反比例函数y=(x>0)的图象上,点D的坐标为(2,6),可求得反比例函数的解析式,又由AB平行于x轴,点A的坐标为(0,3),即可求得点B的坐标,继而求得点C的坐标,然后根据平移的性质,求得答案.
【解答】解:∵D在反比例函数y=(x>0)的图象上,点D的坐标为(2,6),
∴k=xy=2×6=12,
∴反比例函数为:y=,
∵点A的坐标为(0,3),
∴点B的纵坐标为:3,
∴3=,
解得:x=4,
∴点B(4,3),
∵四边形ABCD是平行四边形,
∴点C(6,6),
∴将这个平行四边形向左平移2个单位、再向下平移3个单位后点C的坐标为:(4,3).
故选:B.
3.(4分)公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,则动力F(单位:N)关于动力臂l(单位:m)的函数解析式正确的是( )
A.F= B.F= C.F= D.F=
【分析】直接利用阻力×阻力臂=动力×动力臂,进而将已知量据代入得出函数关系式.
【解答】解:∵阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:1200×0.5=Fl,
则F=.
故选:B.
4.(4分)一个等腰三角形的底边长是6,腰长是一元二次方程x2﹣8x+15=0的一根,则此三角形的周长是( )
A.16 B.12 C.14 D.12或16
【分析】先利用因式分解法解方程求出x的值,再根据三角形三边关系得出三角形的三边长度,继而相加即可得.
【解答】解:解方程x2﹣8x+15=0,得:x=3或x=5,
若腰长为3,则三角形的三边为3、3、6,显然不能构成三角形;
若腰长为5,则三角形三边长为5、5、6,此时三角形的周长为16,
故选:A.
5.(4分)已知关于x的一元二次方程kx2﹣(2k﹣1)x+k﹣2=0有两个不相等的实数根,则实数k的取值范围是( )
A.k>﹣ B.k< C.k>﹣且k≠0 D.k<且k≠0
【分析】利用一元二次方程的定义和判别式的意义得到k≠0且Δ=(2k﹣1)2﹣4k (k﹣2)>0,然后求出两个不等式的公共部分即可.
【解答】解:根据题意得k≠0且Δ=(2k﹣1)2﹣4k (k﹣2)>0,
解得k>﹣且k≠0.
故选:C.
6.(4分)某商场销售一批衬衣,平均每天售出30件,每件衬衣盈利50元.为了增加盈利,尽快减少库存,商场决定采取降价措施.经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.若商场平均每天盈利2000元,则每件衬衣应降价( )
A.10元 B.15元 C.20元 D.25元
【分析】利用平均每天售出的件数×每件盈利=每天的利润列出方程解答即可.
【解答】解:设每件衬衫应降价x元.
根据题意得:(50﹣x)(30+2x)=2000,
整理,得x2﹣35x+250=0,
解得x1=10,x2=25,
∵题目要求扩大销售量,减少库存,
∴x1=10应略去,
∴取x2=25.
故选:D.
7.(4分)如图,已知AB∥CD∥EF,AC:AE=3:5,那么下列结论正确的是( )
A.BD:DF=2:3 B.AB:CD=2:3 C.CD:EF=3:5 D.DF:BF=2:5
【分析】根据平行线分线段成比例定理判断即可.
【解答】解:∵AB∥CD∥EF,
∴BD:DF=AC:CE=3:2,A选项错误,不符合题意;
AB:CD的值无法确定,B选项错误,不符合题意;
CD:EF的值无法确定,C选项错误,不符合题意;
DF:BF=CE:AE=2:5,D选项正确,符合题意;
故选:D.
8.(4分)如图,点E是线段BC的中点,∠B=∠C=∠AED,下列结论中,说法错误的是( )
A.△ABE与△ECD相似 B.△ABE与△AED相似
C. D.∠BAE=∠ADE
【分析】证明△BAE∽△CED,△ABE∽△AED,可得结论.
【解答】解:∵∠AEC=∠AED+∠DEC=∠B+∠BAE,∠B=∠AED,
∴∠DEC=∠BAE,
∵∠B=∠C,
∴△BAE∽△CED,
∴=,
∵BE=CE,
∴=,
∴=,
∵∠B=∠AED,
∴△ABE∽△AED,
∴=,
故选项A,B,C正确,
故选:D.
9.(4分)如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是( )
A.6米 B.8米 C.18米 D.24米
【分析】由已知得△ABP∽△CDP,则根据相似形的性质可得,解答即可.
【解答】解:
由题意知:光线AP与光线PC,∠APB=∠CPD,
∴Rt△ABP∽Rt△CDP,
∴,∴CD==8(米).
故选:B.
10.(4分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )
A.sinA= B.cosA= C.tanA= D.cosB=
【分析】利用同角的余角相等可得∠A=∠BCD,再根据正弦定义可得答案.
【解答】解:∵∠ACB=90°,CD⊥AB,
∴∠A+∠DCA=90°,∠DCA+∠BCD=90°,
∴∠A=∠BCD,
∴sinA=sin∠BCD=,
故选:A.
11.(4分)一艘轮船在A处测得灯塔S在船的南偏东60°方向,轮船继续向正东航行30海里后到达B处,这时测得灯塔S在船的南偏西75°方向,则灯塔S离观测点A、B的距离分别是( )
A.(15﹣15)海里、15海里
B.(15﹣15)海里、5海里
C.(15﹣15)海里、15海里
D.(15﹣15)海里、15海里
【分析】过S作SC⊥AB于C,在AB上截取CD=AC,根据线段垂直平分线的性质得到AS=DS,由等腰三角形的性质得到∠CDS=∠CAS=30°,求得SD=BD,设CS=x,解直角三角形即可得到结论.
【解答】解:过S作SC⊥AB于C,在AB上截取CD=AC,
∴AS=DS,
∴∠CDS=∠CAS=30°,
∵∠ABS=15°,
∴∠DSB=15°,
∴SD=BD,
设CS=x,
在Rt△ASC中,∵∠CAS=30°,
∴AC=x,AS=DS=BD=2x,
∵AB=30海里,
∴x+x+2x=30,
解得:x=,
∴AS=(15﹣15)(海里);
∴BS==15(海里),
∴灯塔S离观测点A、B的距离分别是(15﹣15)海里、15海里,
故选:D.
12.(4分)如图,直线y=kx+b与双曲线交于点A(﹣8,1),B(2,﹣4),与两坐标轴分别交于点C,D,已知点E(1,0),连接AE,BE,作直线ED,将直线ED向上平移n(n>0)个单位长度后,与双曲线有唯一交点,则n的值为( )
A. B. C. D.
【分析】根据A(﹣8,1),B(2,﹣4)解出直线方程解析,双曲线解析式,从而确定直线DE的解析式,将直线ED向上平移n(n>0)个单位长度后,可将平移后的解析式表示出来,与双曲线有唯一交点,则含有n的式子的判别式为零,由此即可求解.
【解答】解:直线y=kx+b与双曲线交于点A(﹣8,1),B(2,﹣4),
∴,,
解得,m=﹣8,
∴直线方程的解析式为,双曲线的解析式为,
∴C(﹣6,0),D(0,﹣3),且E(1,0),
设直线DE的解析式为y=k1x+b1,
∴,
解得,
∴直线DE的解析式为y=3x﹣3,
将直线ED向上平移n(n>0)个单位长度后的解析式为y=3x﹣3+n,与双曲线有唯一交点,
∴,
整理得,3x2+(n﹣3)x+8=0,
∵有唯一解,
∴根的判别式Δ=0,即(n﹣3)2﹣4×3×8=0,且n>0,
∴,
故选:C.
二、填空题(共5题,共20分)
13.(3分)某校来自甲、乙、丙、丁四个社区的学生人数分布如图,若来自甲社区的学生有120人,则该校学生总数为 800 人.
【分析】先根据百分比之和等于1求得甲的百分比,再用甲社区的人数除以其所占百分比可得总人数.
【解答】解:∵甲社区人数所占百分比为1﹣(30%+20%+35%)=15%,
∴该校学生总数为120÷15%=800(人),
故答案为:800.
14.(3分)你吃过兰州拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(cm)是面条粗细(横截面积)x(cm2)的反比例函数,假设其图象如图所示,则y与x的函数关系式为 y=(x>0) .
【分析】根据反比例函数图象,设解析式为,由于点(0.04,3200)在图象上,代入反比例函数即可求得k的值.
【解答】解:设反比例函数图象的解析式为,
由图得,反比例函数上一点坐标为(0.04,3200)代入,有,
解得k=128,又题中实际意义需x>0.
∴y=(x>0).
故答案为:y=(x>0).
15.(3分)如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若Rt△ABC是“好玩三角形”,且∠A=90°,则tan∠ABC= 或 .
【分析】分两种情形分别画出图形求解即可.
【解答】解:①如图1中,
在Rt△ABC中,∠A=90°,CE是△ABC的中线,设AB=EC=2a,则AE=EB=a,AC=a,
∴tan∠ABC==.
②如图2中,
在Rt△ABC中,∠A=90°,BE是△ABC的中线,设EB=AC=2a,则AE=EC=a,AB=a,
∴tan∠ABC==.
故答案为:或.
16.(3分)在Rt△ABC中,∠ACB=90°,AC=3,BC=5,点D是斜边AB上一点(AD>BD)如果将△BCD沿CD所在直线翻折,点B落在点E处,连接AE,当AE⊥AC时,那么的值为 .
【分析】延长AE、CD相交于F,由翻折的性质得出CE=CB=5,∠BCD=∠ECD,再由勾股定理求出AE=4,然后证EF=CE=5,从而得AF=9,最后证△BCD∽△AFD,利用相似三角形的性质求解.
【解答】解:如图,延长AE、CD相交于F,
∵将△BCD沿 CD所在直线翻折,点 B落在点 E处,
∴CE=CB=5,∠BCD=∠ECD,
∵AE⊥AC,
∴∠CAE=90°
∴由勾股定理,得,
∵∠ACB=90°
∴∠ACB+∠CAE=180°,
∴BC∥AE,
∴∠BCD=∠EFD,
∴∠ECD=∠EFD,
∴EF=CE=5,
∴AF=AE+EF=9,
∵BC∥AE,
∴△BCD∽△AFD,
∴,
故答案为:.
17.(3分)有A,B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字0,1,2,3;B布袋中有三个除标号外完全相同的小球,小球上分别标有数字0,1,2.小明先从A布袋中随机取出一个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.若用(m,n)表示小明取球时m与n的对应值,则使关于x的一元二次方程有实数根的概率为 .
【分析】首先根据题意画出树状图,然后由树状图即求得所有等可能的结果,根据树状图,即可求得关于x的一元二次方程有实数根的情况,再利用概率公式求解即可求得答案.
【解答】解:根据题意画出树状图如下:
由图可知,数对(m,n)共有12中等可能结果,
∵关于x的一元二次方程有实数根,
∴Δ=m2﹣2n≥0,
∵在数对(m,n)的12种等可能结果中,能使Δ=m2﹣2n≥0有:(0,0),(1,0),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),共计8种,
∴能使关于x的一元二次方程有实数根的概率.
故答案为:.
三、解答题(共4题,共52分)
18.已知关于x的一元二次方程:x2+(k﹣5)x+4﹣k=0
(1)求证:无论k为何值,方程总有实数根;
(2)若方程的一个根是2,求另一个根及k的值.
【分析】(1)根据根的判别式得出Δ=(k﹣3)2≥0,从而证出无论k取任何值,方程总有实数根.
(2)先把x=2代入原方程,求出k的值,再根据根与系数的关系即可求出方程的另一个根.
【解答】解:(1)∵Δ=(k﹣5)2﹣4×1×(4﹣k)=k2﹣6k+9=(k﹣3)2≥0,
∴无论k取任何值,方程总有实数根.
(2)∵x=2是方程x2+(k﹣5)x+4﹣k=0的一个根,
∴22+(k﹣5)×2+4﹣k=0,
解得:k=2,
设方程的另一个根为x1,则x x1=4﹣k,
即2×x1=2,
x1=1,
则方程的另一个根为1.
19.某校积极开展中学生社会实践活动,决定成立文明宣传、环境保护、交通监督三个志愿者队伍,每名学生最多选择一个队伍.为了了解学生的选择意向,随机抽取A,B,C,D四个班,共200名学生进行调查.将调查得到的数据进行整理,绘制成如下统计图.
(1)求扇形统计图中交通监督所在扇形的圆心角度数;
(2)求D班选择环境保护的学生人数,并补全折线统计图;
(3)若该校共有学生2500人,试估计该校选择文明宣传的学生人数.
【分析】(1)计算出选择交通监督的人数后除以总人数算出百分比后乘以360°即可.
(2)根据扇形图算出环境保护的总人数后减去A、B、C班环境保护人数即可.
(3)根据扇形图计算出文明宣传人数的占比后乘以2500即可.
【解答】解:(1)选择交通监督的人数是12+15+13+14=54(人),
选择交通监督的百分比是54÷200×100%=27%,
扇形统计图中交通监督所在扇形的圆心角度数是360°×27%=97.2°;
(2)D班选择环境保护的学生人数是200×30%﹣15﹣14﹣16=15(人),
补全的折线统计图如图所示.
(3)2500×(1﹣30%﹣27%﹣5%)=950(人),
∴估计该校选择文明宣传的学生人数是950人.
20.为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时60千米的道路AB(如图所示),当无人机在限速道路的正上方C处时,测得限速道路的起点A的俯角是37°,无人机继续向右水平飞行220米到达D处,此时又测得起点A的俯角是30°,同时测得限速道路终点B的俯角是45°(注:即四边形ABDC是梯形).
(1)求限速道路AB的长(精确到1米);
(2)如果李师傅在道路AB上行驶的时间是1分20秒,请判断他是否超速?并说明理由.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73)
【分析】(1)由三角函数定义求出AE、AB,即可得出答案;
(2)求出该汽车的速度,即可得出结论.
【解答】解:(1)根据题意,得∠CAB=37°,CD=220米,∠DAB=30°,∠DBA=45°,
如图,过点C和点D作CE和DF垂直于AB于点E和F,
∵CD∥AB,
∴四边形CDFE是矩形,
∴CE=DF,CD=EF,
∵∠DBA=45°,
∴DF=BF,
设DF=BF=CE=x米,
在Rt△ADF中,∠DAF=30°,DF=x米,
∴AF=DF=x(米),
∴AE=AF﹣EF=(x﹣220)米,
在Rt△AEC中,∠CAE=37°,
∵CE=AE tan37°,
∴x=(x﹣220)×0.75,
解得x=60(3+4)=180+240,
∴AE=x﹣220=(320+240)米,
FB=x=(180+240)(米),
∴AB=AE+EF+FB
=320+240+220+180+240
=780+420
≈1507(米),
答:限速道路AB的长约为1507米;
(2)∵1分20秒=小时,
∴该汽车的速度约为:1507÷≈67.8km/h>60km/h,
∴该车超速.
21.如图,一次函数y=kx+b的图象与反比例函数y=(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)根据图象直接写出kx+b<的x的取值范围;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
【分析】(1)先根据题意得出P点坐标,再将A、P两点的坐标代入y=kx+b求出kb的值,故可得出一次函数的解析式,把点P(4,2)代入反比例函数y=即可得出m的值,进而得出结论;
(2)利用图象法,写出反比例函数图象和一次函数图象的上方的自变量的取值范围即可;
(3)根据菱形的性质即可得出结论.
【解答】解:(1)∵AC=BC,CO⊥AB,A(﹣4,0),
∴O为AB的中点,即OA=OB=4,
∴P(4,2),B(4,0),
将A(﹣4,0)与P(4,2)代入y=kx+b得:
,
解得:,
∴一次函数解析式为y=x+1,
将P(4,2)代入反比例解析式得:m=8,即反比例函数解析式为y=.
(2)观察图象可知,kx+b<时,x的取值范围0<x<4.
(3)如图所示,
∵点C(0,1),B(4,0)
∴BC==,PC=,
∴以BC、PC为边构造菱形,
∵四边形BCPD为菱形,
∴PB垂直且平分CD,
∵PB⊥x轴,P(4,2),
∴点D(8,1),
∵反比例函数解析式为y=,
当x=8时,y=1,
∴点D在反比例函数的图象上.
一、选择题(共12题,共48分)
1.(4分)已知函数y=(m+2)x是反比例函数,则m的值是( )
A.2 B.±2 C.±4 D.±6
2.(4分)如图,平行四边形ABCD的顶点B,D都在反比例函数y=(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形向左平移2个单位、再向下平移3个单位后点C的坐标为( )
A.(1,3) B.(4,3) C.(1,4) D.(2,4)
3.(4分)公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,则动力F(单位:N)关于动力臂l(单位:m)的函数解析式正确的是( )
A.F= B.F= C.F= D.F=
4.(4分)一个等腰三角形的底边长是6,腰长是一元二次方程x2﹣8x+15=0的一根,则此三角形的周长是( )
A.16 B.12 C.14 D.12或16
5.(4分)已知关于x的一元二次方程kx2﹣(2k﹣1)x+k﹣2=0有两个不相等的实数根,则实数k的取值范围是( )
A.k>﹣ B.k< C.k>﹣且k≠0 D.k<且k≠0
6.(4分)某商场销售一批衬衣,平均每天售出30件,每件衬衣盈利50元.为了增加盈利,尽快减少库存,商场决定采取降价措施.经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.若商场平均每天盈利2000元,则每件衬衣应降价( )
A.10元 B.15元 C.20元 D.25元
7.(4分)如图,已知AB∥CD∥EF,AC:AE=3:5,那么下列结论正确的是( )
A.BD:DF=2:3 B.AB:CD=2:3 C.CD:EF=3:5 D.DF:BF=2:5
8.(4分)如图,点E是线段BC的中点,∠B=∠C=∠AED,下列结论中,说法错误的是( )
A.△ABE与△ECD相似 B.△ABE与△AED相似
C. D.∠BAE=∠ADE
9.(4分)如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是( )
A.6米 B.8米 C.18米 D.24米
10.(4分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )
A.sinA= B.cosA= C.tanA= D.cosB=
11.(4分)一艘轮船在A处测得灯塔S在船的南偏东60°方向,轮船继续向正东航行30海里后到达B处,这时测得灯塔S在船的南偏西75°方向,则灯塔S离观测点A、B的距离分别是( )
A.(15﹣15)海里、15海里
B.(15﹣15)海里、5海里
C.(15﹣15)海里、15海里
D.(15﹣15)海里、15海里
12.(4分)如图,直线y=kx+b与双曲线交于点A(﹣8,1),B(2,﹣4),与两坐标轴分别交于点C,D,已知点E(1,0),连接AE,BE,作直线ED,将直线ED向上平移n(n>0)个单位长度后,与双曲线有唯一交点,则n的值为( )
A. B. C. D.
二、填空题(共5题,共20分)
13.(3分)某校来自甲、乙、丙、丁四个社区的学生人数分布如图,若来自甲社区的学生有120人,则该校学生总数为 人.
14.(3分)你吃过兰州拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(cm)是面条粗细(横截面积)x(cm2)的反比例函数,假设其图象如图所示,则y与x的函数关系式为 .
15.(3分)如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若Rt△ABC是“好玩三角形”,且∠A=90°,则tan∠ABC= .
16.(3分)在Rt△ABC中,∠ACB=90°,AC=3,BC=5,点D是斜边AB上一点(AD>BD)如果将△BCD沿CD所在直线翻折,点B落在点E处,连接AE,当AE⊥AC时,那么的值为 .
17.(3分)有A,B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字0,1,2,3;B布袋中有三个除标号外完全相同的小球,小球上分别标有数字0,1,2.小明先从A布袋中随机取出一个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.若用(m,n)表示小明取球时m与n的对应值,则使关于x的一元二次方程有实数根的概率为 .
三、解答题(共4题,共52分)
18.已知关于x的一元二次方程:x2+(k﹣5)x+4﹣k=0
(1)求证:无论k为何值,方程总有实数根;
(2)若方程的一个根是2,求另一个根及k的值.
19.某校积极开展中学生社会实践活动,决定成立文明宣传、环境保护、交通监督三个志愿者队伍,每名学生最多选择一个队伍.为了了解学生的选择意向,随机抽取A,B,C,D四个班,共200名学生进行调查.将调查得到的数据进行整理,绘制成如下统计图.
(1)求扇形统计图中交通监督所在扇形的圆心角度数;
(2)求D班选择环境保护的学生人数,并补全折线统计图;
(3)若该校共有学生2500人,试估计该校选择文明宣传的学生人数.
20.为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时60千米的道路AB(如图所示),当无人机在限速道路的正上方C处时,测得限速道路的起点A的俯角是37°,无人机继续向右水平飞行220米到达D处,此时又测得起点A的俯角是30°,同时测得限速道路终点B的俯角是45°(注:即四边形ABDC是梯形).
(1)求限速道路AB的长(精确到1米);
(2)如果李师傅在道路AB上行驶的时间是1分20秒,请判断他是否超速?并说明理由.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73)
21.如图,一次函数y=kx+b的图象与反比例函数y=(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)根据图象直接写出kx+b<的x的取值范围;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
2022-2023学年湖南省益阳市桃江县三校联考九年级(上)期末数学试卷
参考答案与试题解析
一、选择题(共12题,共48分)
1.(4分)已知函数y=(m+2)x是反比例函数,则m的值是( )
A.2 B.±2 C.±4 D.±6
【分析】根据反比例函数的定义得到m2﹣5=﹣1,且m+2≠0,由此求得m的值.
【解答】解:依题意得:m2﹣5=﹣1,且m+2≠0,
解得m=2.
故选:A.
2.(4分)如图,平行四边形ABCD的顶点B,D都在反比例函数y=(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形向左平移2个单位、再向下平移3个单位后点C的坐标为( )
A.(1,3) B.(4,3) C.(1,4) D.(2,4)
【分析】由平行四边形ABCD的顶点B,D都在反比例函数y=(x>0)的图象上,点D的坐标为(2,6),可求得反比例函数的解析式,又由AB平行于x轴,点A的坐标为(0,3),即可求得点B的坐标,继而求得点C的坐标,然后根据平移的性质,求得答案.
【解答】解:∵D在反比例函数y=(x>0)的图象上,点D的坐标为(2,6),
∴k=xy=2×6=12,
∴反比例函数为:y=,
∵点A的坐标为(0,3),
∴点B的纵坐标为:3,
∴3=,
解得:x=4,
∴点B(4,3),
∵四边形ABCD是平行四边形,
∴点C(6,6),
∴将这个平行四边形向左平移2个单位、再向下平移3个单位后点C的坐标为:(4,3).
故选:B.
3.(4分)公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,则动力F(单位:N)关于动力臂l(单位:m)的函数解析式正确的是( )
A.F= B.F= C.F= D.F=
【分析】直接利用阻力×阻力臂=动力×动力臂,进而将已知量据代入得出函数关系式.
【解答】解:∵阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:1200×0.5=Fl,
则F=.
故选:B.
4.(4分)一个等腰三角形的底边长是6,腰长是一元二次方程x2﹣8x+15=0的一根,则此三角形的周长是( )
A.16 B.12 C.14 D.12或16
【分析】先利用因式分解法解方程求出x的值,再根据三角形三边关系得出三角形的三边长度,继而相加即可得.
【解答】解:解方程x2﹣8x+15=0,得:x=3或x=5,
若腰长为3,则三角形的三边为3、3、6,显然不能构成三角形;
若腰长为5,则三角形三边长为5、5、6,此时三角形的周长为16,
故选:A.
5.(4分)已知关于x的一元二次方程kx2﹣(2k﹣1)x+k﹣2=0有两个不相等的实数根,则实数k的取值范围是( )
A.k>﹣ B.k< C.k>﹣且k≠0 D.k<且k≠0
【分析】利用一元二次方程的定义和判别式的意义得到k≠0且Δ=(2k﹣1)2﹣4k (k﹣2)>0,然后求出两个不等式的公共部分即可.
【解答】解:根据题意得k≠0且Δ=(2k﹣1)2﹣4k (k﹣2)>0,
解得k>﹣且k≠0.
故选:C.
6.(4分)某商场销售一批衬衣,平均每天售出30件,每件衬衣盈利50元.为了增加盈利,尽快减少库存,商场决定采取降价措施.经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.若商场平均每天盈利2000元,则每件衬衣应降价( )
A.10元 B.15元 C.20元 D.25元
【分析】利用平均每天售出的件数×每件盈利=每天的利润列出方程解答即可.
【解答】解:设每件衬衫应降价x元.
根据题意得:(50﹣x)(30+2x)=2000,
整理,得x2﹣35x+250=0,
解得x1=10,x2=25,
∵题目要求扩大销售量,减少库存,
∴x1=10应略去,
∴取x2=25.
故选:D.
7.(4分)如图,已知AB∥CD∥EF,AC:AE=3:5,那么下列结论正确的是( )
A.BD:DF=2:3 B.AB:CD=2:3 C.CD:EF=3:5 D.DF:BF=2:5
【分析】根据平行线分线段成比例定理判断即可.
【解答】解:∵AB∥CD∥EF,
∴BD:DF=AC:CE=3:2,A选项错误,不符合题意;
AB:CD的值无法确定,B选项错误,不符合题意;
CD:EF的值无法确定,C选项错误,不符合题意;
DF:BF=CE:AE=2:5,D选项正确,符合题意;
故选:D.
8.(4分)如图,点E是线段BC的中点,∠B=∠C=∠AED,下列结论中,说法错误的是( )
A.△ABE与△ECD相似 B.△ABE与△AED相似
C. D.∠BAE=∠ADE
【分析】证明△BAE∽△CED,△ABE∽△AED,可得结论.
【解答】解:∵∠AEC=∠AED+∠DEC=∠B+∠BAE,∠B=∠AED,
∴∠DEC=∠BAE,
∵∠B=∠C,
∴△BAE∽△CED,
∴=,
∵BE=CE,
∴=,
∴=,
∵∠B=∠AED,
∴△ABE∽△AED,
∴=,
故选项A,B,C正确,
故选:D.
9.(4分)如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是( )
A.6米 B.8米 C.18米 D.24米
【分析】由已知得△ABP∽△CDP,则根据相似形的性质可得,解答即可.
【解答】解:
由题意知:光线AP与光线PC,∠APB=∠CPD,
∴Rt△ABP∽Rt△CDP,
∴,∴CD==8(米).
故选:B.
10.(4分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )
A.sinA= B.cosA= C.tanA= D.cosB=
【分析】利用同角的余角相等可得∠A=∠BCD,再根据正弦定义可得答案.
【解答】解:∵∠ACB=90°,CD⊥AB,
∴∠A+∠DCA=90°,∠DCA+∠BCD=90°,
∴∠A=∠BCD,
∴sinA=sin∠BCD=,
故选:A.
11.(4分)一艘轮船在A处测得灯塔S在船的南偏东60°方向,轮船继续向正东航行30海里后到达B处,这时测得灯塔S在船的南偏西75°方向,则灯塔S离观测点A、B的距离分别是( )
A.(15﹣15)海里、15海里
B.(15﹣15)海里、5海里
C.(15﹣15)海里、15海里
D.(15﹣15)海里、15海里
【分析】过S作SC⊥AB于C,在AB上截取CD=AC,根据线段垂直平分线的性质得到AS=DS,由等腰三角形的性质得到∠CDS=∠CAS=30°,求得SD=BD,设CS=x,解直角三角形即可得到结论.
【解答】解:过S作SC⊥AB于C,在AB上截取CD=AC,
∴AS=DS,
∴∠CDS=∠CAS=30°,
∵∠ABS=15°,
∴∠DSB=15°,
∴SD=BD,
设CS=x,
在Rt△ASC中,∵∠CAS=30°,
∴AC=x,AS=DS=BD=2x,
∵AB=30海里,
∴x+x+2x=30,
解得:x=,
∴AS=(15﹣15)(海里);
∴BS==15(海里),
∴灯塔S离观测点A、B的距离分别是(15﹣15)海里、15海里,
故选:D.
12.(4分)如图,直线y=kx+b与双曲线交于点A(﹣8,1),B(2,﹣4),与两坐标轴分别交于点C,D,已知点E(1,0),连接AE,BE,作直线ED,将直线ED向上平移n(n>0)个单位长度后,与双曲线有唯一交点,则n的值为( )
A. B. C. D.
【分析】根据A(﹣8,1),B(2,﹣4)解出直线方程解析,双曲线解析式,从而确定直线DE的解析式,将直线ED向上平移n(n>0)个单位长度后,可将平移后的解析式表示出来,与双曲线有唯一交点,则含有n的式子的判别式为零,由此即可求解.
【解答】解:直线y=kx+b与双曲线交于点A(﹣8,1),B(2,﹣4),
∴,,
解得,m=﹣8,
∴直线方程的解析式为,双曲线的解析式为,
∴C(﹣6,0),D(0,﹣3),且E(1,0),
设直线DE的解析式为y=k1x+b1,
∴,
解得,
∴直线DE的解析式为y=3x﹣3,
将直线ED向上平移n(n>0)个单位长度后的解析式为y=3x﹣3+n,与双曲线有唯一交点,
∴,
整理得,3x2+(n﹣3)x+8=0,
∵有唯一解,
∴根的判别式Δ=0,即(n﹣3)2﹣4×3×8=0,且n>0,
∴,
故选:C.
二、填空题(共5题,共20分)
13.(3分)某校来自甲、乙、丙、丁四个社区的学生人数分布如图,若来自甲社区的学生有120人,则该校学生总数为 800 人.
【分析】先根据百分比之和等于1求得甲的百分比,再用甲社区的人数除以其所占百分比可得总人数.
【解答】解:∵甲社区人数所占百分比为1﹣(30%+20%+35%)=15%,
∴该校学生总数为120÷15%=800(人),
故答案为:800.
14.(3分)你吃过兰州拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(cm)是面条粗细(横截面积)x(cm2)的反比例函数,假设其图象如图所示,则y与x的函数关系式为 y=(x>0) .
【分析】根据反比例函数图象,设解析式为,由于点(0.04,3200)在图象上,代入反比例函数即可求得k的值.
【解答】解:设反比例函数图象的解析式为,
由图得,反比例函数上一点坐标为(0.04,3200)代入,有,
解得k=128,又题中实际意义需x>0.
∴y=(x>0).
故答案为:y=(x>0).
15.(3分)如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若Rt△ABC是“好玩三角形”,且∠A=90°,则tan∠ABC= 或 .
【分析】分两种情形分别画出图形求解即可.
【解答】解:①如图1中,
在Rt△ABC中,∠A=90°,CE是△ABC的中线,设AB=EC=2a,则AE=EB=a,AC=a,
∴tan∠ABC==.
②如图2中,
在Rt△ABC中,∠A=90°,BE是△ABC的中线,设EB=AC=2a,则AE=EC=a,AB=a,
∴tan∠ABC==.
故答案为:或.
16.(3分)在Rt△ABC中,∠ACB=90°,AC=3,BC=5,点D是斜边AB上一点(AD>BD)如果将△BCD沿CD所在直线翻折,点B落在点E处,连接AE,当AE⊥AC时,那么的值为 .
【分析】延长AE、CD相交于F,由翻折的性质得出CE=CB=5,∠BCD=∠ECD,再由勾股定理求出AE=4,然后证EF=CE=5,从而得AF=9,最后证△BCD∽△AFD,利用相似三角形的性质求解.
【解答】解:如图,延长AE、CD相交于F,
∵将△BCD沿 CD所在直线翻折,点 B落在点 E处,
∴CE=CB=5,∠BCD=∠ECD,
∵AE⊥AC,
∴∠CAE=90°
∴由勾股定理,得,
∵∠ACB=90°
∴∠ACB+∠CAE=180°,
∴BC∥AE,
∴∠BCD=∠EFD,
∴∠ECD=∠EFD,
∴EF=CE=5,
∴AF=AE+EF=9,
∵BC∥AE,
∴△BCD∽△AFD,
∴,
故答案为:.
17.(3分)有A,B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字0,1,2,3;B布袋中有三个除标号外完全相同的小球,小球上分别标有数字0,1,2.小明先从A布袋中随机取出一个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.若用(m,n)表示小明取球时m与n的对应值,则使关于x的一元二次方程有实数根的概率为 .
【分析】首先根据题意画出树状图,然后由树状图即求得所有等可能的结果,根据树状图,即可求得关于x的一元二次方程有实数根的情况,再利用概率公式求解即可求得答案.
【解答】解:根据题意画出树状图如下:
由图可知,数对(m,n)共有12中等可能结果,
∵关于x的一元二次方程有实数根,
∴Δ=m2﹣2n≥0,
∵在数对(m,n)的12种等可能结果中,能使Δ=m2﹣2n≥0有:(0,0),(1,0),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),共计8种,
∴能使关于x的一元二次方程有实数根的概率.
故答案为:.
三、解答题(共4题,共52分)
18.已知关于x的一元二次方程:x2+(k﹣5)x+4﹣k=0
(1)求证:无论k为何值,方程总有实数根;
(2)若方程的一个根是2,求另一个根及k的值.
【分析】(1)根据根的判别式得出Δ=(k﹣3)2≥0,从而证出无论k取任何值,方程总有实数根.
(2)先把x=2代入原方程,求出k的值,再根据根与系数的关系即可求出方程的另一个根.
【解答】解:(1)∵Δ=(k﹣5)2﹣4×1×(4﹣k)=k2﹣6k+9=(k﹣3)2≥0,
∴无论k取任何值,方程总有实数根.
(2)∵x=2是方程x2+(k﹣5)x+4﹣k=0的一个根,
∴22+(k﹣5)×2+4﹣k=0,
解得:k=2,
设方程的另一个根为x1,则x x1=4﹣k,
即2×x1=2,
x1=1,
则方程的另一个根为1.
19.某校积极开展中学生社会实践活动,决定成立文明宣传、环境保护、交通监督三个志愿者队伍,每名学生最多选择一个队伍.为了了解学生的选择意向,随机抽取A,B,C,D四个班,共200名学生进行调查.将调查得到的数据进行整理,绘制成如下统计图.
(1)求扇形统计图中交通监督所在扇形的圆心角度数;
(2)求D班选择环境保护的学生人数,并补全折线统计图;
(3)若该校共有学生2500人,试估计该校选择文明宣传的学生人数.
【分析】(1)计算出选择交通监督的人数后除以总人数算出百分比后乘以360°即可.
(2)根据扇形图算出环境保护的总人数后减去A、B、C班环境保护人数即可.
(3)根据扇形图计算出文明宣传人数的占比后乘以2500即可.
【解答】解:(1)选择交通监督的人数是12+15+13+14=54(人),
选择交通监督的百分比是54÷200×100%=27%,
扇形统计图中交通监督所在扇形的圆心角度数是360°×27%=97.2°;
(2)D班选择环境保护的学生人数是200×30%﹣15﹣14﹣16=15(人),
补全的折线统计图如图所示.
(3)2500×(1﹣30%﹣27%﹣5%)=950(人),
∴估计该校选择文明宣传的学生人数是950人.
20.为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时60千米的道路AB(如图所示),当无人机在限速道路的正上方C处时,测得限速道路的起点A的俯角是37°,无人机继续向右水平飞行220米到达D处,此时又测得起点A的俯角是30°,同时测得限速道路终点B的俯角是45°(注:即四边形ABDC是梯形).
(1)求限速道路AB的长(精确到1米);
(2)如果李师傅在道路AB上行驶的时间是1分20秒,请判断他是否超速?并说明理由.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73)
【分析】(1)由三角函数定义求出AE、AB,即可得出答案;
(2)求出该汽车的速度,即可得出结论.
【解答】解:(1)根据题意,得∠CAB=37°,CD=220米,∠DAB=30°,∠DBA=45°,
如图,过点C和点D作CE和DF垂直于AB于点E和F,
∵CD∥AB,
∴四边形CDFE是矩形,
∴CE=DF,CD=EF,
∵∠DBA=45°,
∴DF=BF,
设DF=BF=CE=x米,
在Rt△ADF中,∠DAF=30°,DF=x米,
∴AF=DF=x(米),
∴AE=AF﹣EF=(x﹣220)米,
在Rt△AEC中,∠CAE=37°,
∵CE=AE tan37°,
∴x=(x﹣220)×0.75,
解得x=60(3+4)=180+240,
∴AE=x﹣220=(320+240)米,
FB=x=(180+240)(米),
∴AB=AE+EF+FB
=320+240+220+180+240
=780+420
≈1507(米),
答:限速道路AB的长约为1507米;
(2)∵1分20秒=小时,
∴该汽车的速度约为:1507÷≈67.8km/h>60km/h,
∴该车超速.
21.如图,一次函数y=kx+b的图象与反比例函数y=(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)根据图象直接写出kx+b<的x的取值范围;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
【分析】(1)先根据题意得出P点坐标,再将A、P两点的坐标代入y=kx+b求出kb的值,故可得出一次函数的解析式,把点P(4,2)代入反比例函数y=即可得出m的值,进而得出结论;
(2)利用图象法,写出反比例函数图象和一次函数图象的上方的自变量的取值范围即可;
(3)根据菱形的性质即可得出结论.
【解答】解:(1)∵AC=BC,CO⊥AB,A(﹣4,0),
∴O为AB的中点,即OA=OB=4,
∴P(4,2),B(4,0),
将A(﹣4,0)与P(4,2)代入y=kx+b得:
,
解得:,
∴一次函数解析式为y=x+1,
将P(4,2)代入反比例解析式得:m=8,即反比例函数解析式为y=.
(2)观察图象可知,kx+b<时,x的取值范围0<x<4.
(3)如图所示,
∵点C(0,1),B(4,0)
∴BC==,PC=,
∴以BC、PC为边构造菱形,
∵四边形BCPD为菱形,
∴PB垂直且平分CD,
∵PB⊥x轴,P(4,2),
∴点D(8,1),
∵反比例函数解析式为y=,
当x=8时,y=1,
∴点D在反比例函数的图象上.
同课章节目录
