九年级数学28章锐角三角函数导学案
文档属性
| 名称 | 九年级数学28章锐角三角函数导学案 |  | |
| 格式 | zip | ||
| 文件大小 | 418.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-12 13:54:37 | ||
图片预览




文档简介
课题:28.1锐角三角函数(总课时12节)
【学习目标】
1经历当直角三角形的锐角固定时,它的对边与斜边的比值、邻边与斜边的比值都固定这一事实。
2 能根据正弦、余弦概念正确进行计算并掌握特殊三角函数值
【学习重点】
理解正弦、余弦(sinA、cosA)概念.
【学习难点】
理解正弦、余弦概念并熟记特殊三角函数值。
【导学过程】
一、自学提纲:
1、如图在Rt△ABC中,∠C=90°,∠A=30°,BC=10m,求AB、AC
2、如图在Rt△ABC中,∠C=90°,∠A=30°,AB=20m,求BC、AC
结论:直角三角形中,30°角的对边与斜边的比值
思考2:在Rt△ABC中,∠C=90°,∠A=45°,∠A对边与斜边
的比值是一个定值吗?如果是,是多少?
结论:直角三角形中,45°角的对边与斜边的比值
探究:任意画Rt△ABC和Rt△A′B′C′,使得∠C=∠C′=90°,
∠A=∠A′=a,那么有什么关系.你能解释一下吗?
结论:这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比
正弦函数概念:
规定:在Rt△BC中,∠C=90,∠A的对边记作a,∠B的对边记作b,∠C的对边记作c.
在Rt△BC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦,
记作sinA,即sinA= =. sinA=
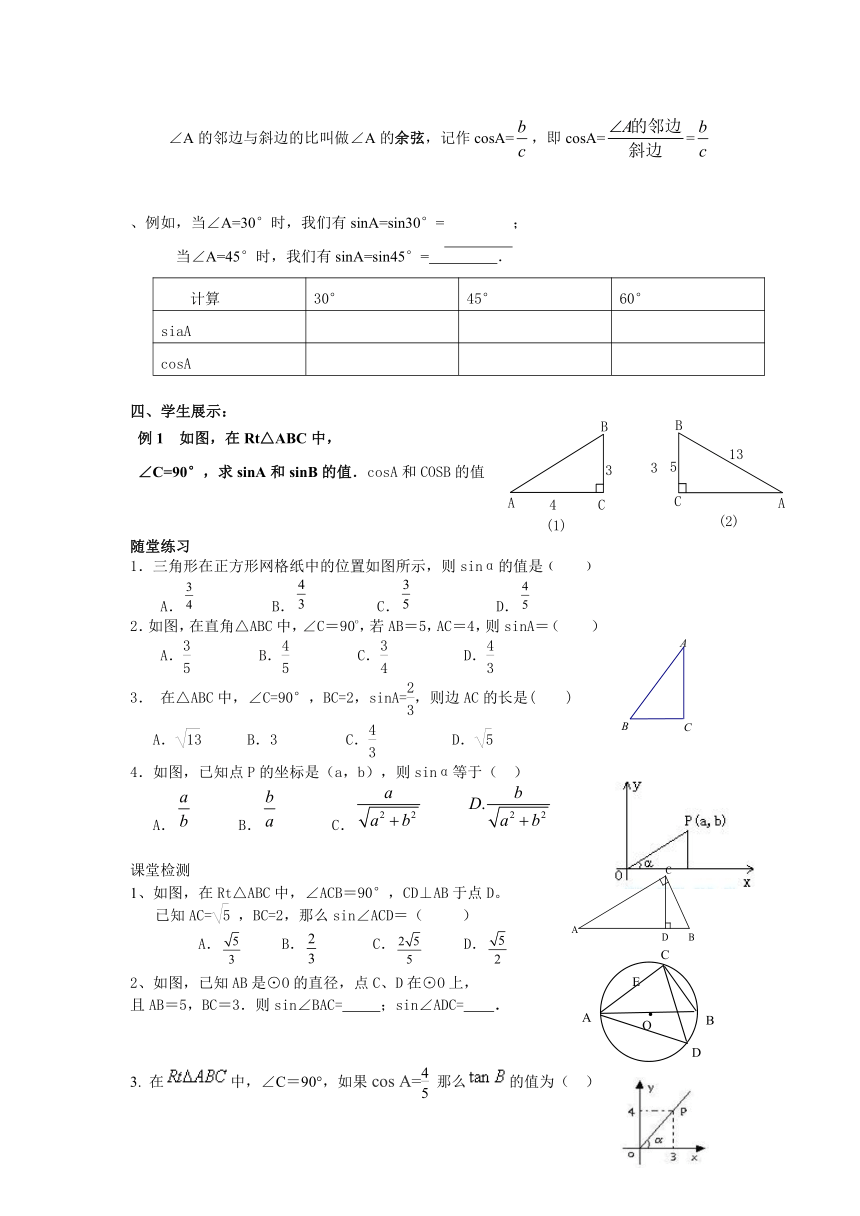
∠A的邻边与斜边的比叫做∠A的余弦,记作cosA=,即cosA==
、例如,当∠A=30°时,我们有sinA=sin30°= ;
当∠A=45°时,我们有sinA=sin45°= .
计算 30° 45° 60°
siaA
cosA
四、学生展示:
例1 如图,在Rt△ABC中,
∠C=90°,求sinA和sinB的值.cosA和COSB的值
随堂练习
1.三角形在正方形网格纸中的位置如图所示,则sinα的值是﹙ ﹚
A.
B.
C.
D.
2.如图,在直角△ABC中,∠C=90o,若AB=5,AC=4,则sinA=( )
A. B. C. D.
3. 在△ABC中,∠C=90°,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
4.如图,已知点P的坐标是(a,b),则sinα等于( )
A. B. C.
课堂检测
1、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D。
已知AC=,BC=2,那么sin∠ACD=( )
A. B. C. D.
2、如图,已知AB是⊙O的直径,点C、D在⊙O上,
且AB=5,BC=3.则sin∠BAC= ;sin∠ADC= .
3. 在中,∠C=90°,如果cos A=那么的值为(?)
A.?B.?C.?D.
分析 本题主要考查锐解三角函数及三角变换知识。其思路是:依据条件
如图:P是∠的边OA上一点,且P点的坐标为(3,4),
则cosα=_____________.
课题:28.1锐角三角函数(总课时13)
【学习目标】
1: 感知当直角三角形的锐角固定时,它的邻边与斜边、对边与邻边的比值也都固定这一事实。
2:逐步培养学生观察、比较、分析、概括的思维能力。
重点:难点:
【学习重点】
理解余弦、正切的概念。
【学习难点】
熟练运用锐角三角函数的概念进行有关计算。
【导学过程】
一、自学提纲:
1、我们是怎样定义直角三角形中一个锐角的正弦的?
2、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D。
已知AC=,BC=2,那么sin∠ACD=( )
A. B. C. D.
3、如图,已知AB是⊙O的直径,点C、D在⊙O上,
且AB=5,BC=3.则sin∠BAC= ;sin∠ADC= .
4、在Rt△ABC中,∠C=90°,当锐角A确定时,
∠A的对边与斜边的比是 ,
现在我们要问:
∠A的邻边与斜边的比呢?
∠A的对边与邻边的比呢?
为什么?
二、合作交流:
探究:
一般地,当∠A取其他一定度数的锐角时,它的邻边与斜边的比是否也是一个固定值?
如图:Rt△ABC与Rt△A`B`C`,∠C=∠C` =90o,∠B=∠B`=α,
那么与有什么关系?
三、教师点拨:
类似于正弦的情况,
如图在Rt△BC中,∠C=90°,当锐角A的大小确定时,∠A的邻边与斜边的比、∠A的对边与邻边的比也分别是确定的.我们
把∠A的对边与邻边的比叫做∠A的正切,记作tanA,即tanA==.
例如,当∠A=30°时,我们有cosA=cos30°= ;
当∠A=45°时,我们有tanA=tan45°= .
(教师讲解并板书):锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,cosA,tanA也是A的函数.
例2:如图,在Rt△ABC中,∠C=90°,BC=6,sinA=,求cosA、tanB的值.
四、学生展示:
练习一:完成课本P81 练习1、2、3
练习二:
1.?在中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,则有(?)
A.?B.?C.?D.
本题主要考查锐解三角函数的定义,同学们只要依据
五、课堂小结:
在Rt△BC中,∠C=90°,我们把
锐角A的对边与斜边的比叫做∠A的正弦,
记作sinA,即sinA= =. sinA=
把∠A的邻边与斜边的比叫做∠A的余弦,
记作 ,即
把∠A的对边与邻边的比叫做∠A的正切,
记作 ,即
课题:28.1锐角三角函数(总课时14)
【学习目标】
⑴: 能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数。
⑵: 能熟练计算含有30°、45°、60°角的三角函数的运算式
【学习重点】
熟记30°、45°、60°角的三角函数值,能熟练计算含有30°、45°、60°角的三角函数的运算式
【学习难点】
30°、45°、60°角的三角函数值的推导过程
【导学过程】
一、自学提纲:
一个直角三角形中,
一个锐角正弦是怎么定义的?
一个锐角余弦是怎么定义的?
一个锐角正切是怎么定义的?
二、合作交流:
思考:
两块三角尺中有几个不同的锐角?
是多少度?
你能分别求出这几个锐角的正弦值、余弦值和正切值码?.
三、教师点拨:
归纳结果
30° 45° 60°
siaA
cosA
tanA
例3:求下列各式的值.
(1)cos260°+sin260°. (2)-tan45°.
例4:(1)如图(1),在Rt△ABC中,∠C=90,AB=,BC=,求∠A的度数.
(2)如图(2),已知圆锥的高AO等于圆锥的底面半径OB的倍,求a.
四、学生展示:
一、课本83页 第1 题
课本83页 第 2题
二、选择题.
1.已知:Rt△ABC中,∠C=90°,cosA=,AB=15,则AC的长是( ).
A.3 B.6 C.9 D.12
2.下列各式中不正确的是( ).
A.sin260°+cos260°=1 B.sin30°+cos30°=1
C.sin35°=cos55° D.tan45°>sin45°
3.计算2sin30°-2cos60°+tan45°的结果是( ).
A.2 B. C. D.1
4.已知∠A为锐角,且cosA≤,那么( )
A.0°<∠A≤60°B.60°≤∠A<90° C.0°<∠A≤30°D.30°≤∠A<90°
5.在△ABC中,∠A、∠B都是锐角,且sinA=,
cosB= eq \f(,2) ,则△ABC的形状是( )
A.直角三角形 B.钝角三角形C.锐角三角形 D.不能确定
6.如图Rt△ABC中,∠ACB=90°,CD⊥AB于D,BC=3,AC=4,设∠BCD=a,则tana的值为( ).
A. B. C. D.
7.当锐角a>60°时,cosa的值( ).
A.小于 B.大于 C.大于 eq \f(,2) D.大于1
8.在△ABC中,三边之比为a:b:c=1::2,则sinA+tanA等于( ).
A.
9.已知梯形ABCD中,腰BC长为2,梯形对角线BD垂直平分AC,若梯形的高是,则∠CAB等于( )
A.30° B.60° C.45° D.以上都不对
10.sin272°+sin218°的值是( ).
A.1 B.0 C. D. eq \f(,2)
11.若(tanA-3)2+│2cosB-│=0,则△ABC( ).
A.是直角三角形 B.是等边三角形
C.是含有60°的任意三角形 D.是顶角为钝角的等腰三角形
三、填空题.
12.设α、β均为锐角,且sinα-cosβ=0,则α+β=_______.
13.的值是_______.
14.已知,等腰△ABC的腰长为4,底为30°,则底边上的高为______,周长为______.
15.在Rt△ABC中,∠C=90°,已知tanB= eq \f(,2) ,则cosA=________.
五、课堂小结:要牢记下表:
30° 45° 60°
siaA
cosA
tanA
六、作业设置:
课本 第85页 习题28.1复习巩固第3题
七、自我反思:
本节课我的收获: 。
课题:28.1锐角三角函数(总课时15)
【学习目标】
让学生熟识计算器一些功能键的使用
【学习重点】
运用计算器处理三角函数中的值或角的问题
【学习难点】
知道值求角的处理
【导学过程】
求下列各式的值.
(1)sin30°·cos45°+cos60°; (2)2sin60°-2cos30°·sin45°
(3); (4)-sin60°(1-sin30°).
(5)tan45°·sin60°-4sin30°·cos45°+·tan30°
(6)+cos45°·cos30°
合作交流:
学生去完成课本83 84页
学生展示:
用计算器求锐角的正弦、余弦、正切值
学生去完成课本83 86页的题目
自我反思:
本节课我的收获: 。
课题:28.2解直角三角形(1)(总课时16)
【学习目标】
1: 使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形
2: 通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.
3: 渗透数形结合的数学思想,培养学生良好的学习习惯.
【学习重点】
直角三角形的解法.
【学习难点】
三角函数在解直角三角形中的灵活运用
【导学过程】
一、自学提纲:
1.在三角形中共有几个元素?
2.直角三角形ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
(1)边角之间关系
如果用表示直角三角形的一个锐角,那上述式子就可以写成.
(2)三边之间关系 (3)锐角之间关系∠A+∠B=90°.
a2 +b2 =c2 (勾股定理) 以上三点正是解直角三角形的依据.
二、合作交流:
要想使人安全地攀上斜靠在墙面上的梯子的顶端.梯子与地面所成的角一般要满足, (如图).现有一个长6m的梯子,问:
(1)使用这个梯子最高可以安全攀上多高的墙(精确到0. 1 m)
(2)当梯子底端距离墙面2.4 m时,梯子与地面所成的角等于多少(精确到1o) 这时人是否能够安全使用这个梯子
三、教师点拨:
例1在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且b=,
a=,解这个三角形.
例2在Rt△ABC中, ∠B =35o,b=20,解这个三角形.
四、学生展示:
完成课本91页练习
补充题
1.根据直角三角形的__________元素(至少有一个边),求出________其它所有元素的过程,即解直角三角形.
2、在Rt△ABC中,a=104.0,b=20.49,解这个三角形.
3、 在△ABC中,∠C为直角,AC=6,的平分线AD=4,解此直角三角形。
4、Rt△ABC中,若sinA=,AB=10,那么BC=_____,tanB=______.
5、在△ABC中,∠C=90°,AC=6,BC=8,那么sinA=________.
6、在△ABC中,∠C=90°,sinA=,则cosA的值是( )
A. B. C.
五、课堂小结:
小结“已知一边一角,如何解直角三角形?”
六、作业设置:
课本 第96页 习题28.2复习巩固第1题、第2题.
七、自我反思:
本节课我的收获: 。
课题:28.2解直角三角形(2)(总课时17)
【学习目标】
⑴: 使学生了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.
⑵: 逐步培养学生分析问题、解决问题的能力.
⑶: 渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识
【学习重点】
将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.
【学习难点】
实际问题转化成数学模型
【导学过程】
一、自学提纲:
1.解直角三角形指什么?
2.解直角三角形主要依据什么?
(1)勾股定理:
(2)锐角之间的关系:
(3)边角之间的关系:
tanA=
二、合作交流:
仰角、俯角
当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.
三、教师点拨:
例3 2003年10月15日“神舟”5号载人航天飞船发射成功.当飞船完成变轨后,就在离地球表面350km的圆形轨道上运行.如图,当飞船运行到地球表面上P点的正上方时,从飞船上最远能直接看到的地球上的点在什么位置 这样的最远点与P点的距离是多少 (地球半径约为6 400 km,结果精确到0. 1 km)
例4热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30o,看这栋离楼底部的俯角为60o,热气球与高楼的水平距离为120 m.这栋高楼有多高(结果精确到0.1m)
四、学生展示:
一、课本93页 练习 第1 、2题
五、课堂小结:
六、作业设置:
课本 第96页 习题28.2复习巩固第3、4题
七、自我反思:
本节课我的收获: 。
课题:28.2解直角三角形(3)(总课时18)
【学习目标】
⑴: 使学生了解方位角的命名特点,能准确把握所指的方位角是指哪一个角
⑵: 逐步培养学生分析问题、解决问题的能力;渗透数形结合的数学思想和方法.
⑶: 巩固用三角函数有关知识解决问题,学会解决方位角问题.
【学习重点】
用三角函数有关知识解决方位角问题
【学习难点】
学会准确分析问题并将实际问题转化成数学模型
【导学过程】
一、自学提纲:
坡度与坡角
坡面的铅直高度h和水平宽度的比叫做坡度(或叫做坡比),
一般用i表示。即i=,常写成i=1:m的形式如i=1:2.5
把坡面与水平面的夹角α叫做坡角.
结合图形思考,坡度i与坡角α之间具有什么关系?
这一关系在实际问题中经常用到。
二、教师点拨:
例5如图,一艘海轮位于灯塔P的北偏东65方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34方向上的B处.这时,海轮所在的B处距离灯塔P有多远?
例6同学们,如果你是修建三峡大坝的工程师,现在有这样一个问题请你解决:如图6-33
水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求斜坡AB的坡面角α,坝底宽AD和斜坡AB的长(精确到0.1m)
四、学生展示:
完成课本91页练习
补充练习
(1)一段坡面的坡角为60°,则坡度i=______;
______,
坡角______度.
2、利用土埂修筑一条渠道,在埂中间挖去深为0.6米的一块(图阴影部分是挖去部分),已知渠道内坡度为1∶1.5,渠道底面宽BC为0.5米,求:
①横断面(等腰梯形)ABCD的面积;
②修一条长为100米的渠道要挖去的土方数.
五、课堂小结:
六、作业设置:
课本 第96页 习题28.2复习巩固第5、6、7题
七、自我反思:
本节课我的收获: 。
课题:锐角三角函数定义检测 (总课时19)
学习要求
理解一个锐角的正弦、余弦、正切的定义.能依据锐角三角函数的定义,求给定锐角的三角函数值.
课堂学习检测
一、填空题
1.如图所示,B、B′是∠MAN的AN边上的任意两点,BC⊥AM于C点,B′C′⊥AM于C′点,则△B'AC′∽______,从而,又可得
①______,即在Rt△ABC中(∠C=90°),当∠A确定时,它的______与______的比是一个______值;
②______,即在Rt△ABC中(∠C=90°),当∠A确定时,它的______与______的比也是一个______;
③______,即在Rt△ABC中(∠C=90°),当∠A确定时,它的______与______的比还是一个______.
第1题图
2.如图所示,在Rt△ABC中,∠C=90°.
第2题图
①=______, =______;
②=______, =______;
③=______, =______.
3.因为对于锐角 的每一个确定的值,sin 、cos 、tan 分别都有____________与它______,所以sin 、cos 、tan 都是____________.又称为 的____________.
4.在Rt△ABC中,∠C=90°,若a=9,b=12,则c=______,
sinA=______,cosA=______,tanA=______,
sinB=______,cosB=______,tanB=______.
5.在Rt△ABC中,∠C=90°,若a=1,b=3,则c=______,
sinA=______,cosA=______,tanA=______,
sinB=______,cosB=______,tanB=______.
6.在Rt△ABC中,∠B=90°,若a=16,c=30,则b=______,
sinA=______,cosA=______,tanA=______,
sinC=______,cosC=______,tanC=______.
7.在Rt△ABC中,∠C=90°,若∠A=30°,则∠B=______,
sinA=______,cosA=______,tanA=______,
sinB=______,cosB=______,tanB=______.
二、解答题
8.已知:如图,Rt△TNM中,∠TMN=90°,MR⊥TN于R点,TN=4,MN=3.
求:sin∠TMR、cos∠TMR、tan∠TMR.
9.已知Rt△ABC中,求AC、AB和cosB.
综合、运用、诊断
10.已知:如图,Rt△ABC中,∠C=90°.D是AC边上一点,DE⊥AB于E点.
DE∶AE=1∶2.
求:sinB、cosB、tanB.
11.已知:如图,⊙O的半径OA=16cm,OC⊥AB于C点,
求:AB及OC的长.
12.已知:⊙O中,OC⊥AB于C点,AB=16cm,
(1)求⊙O的半径OA的长及弦心距OC;
(2)求cos∠AOC及tan∠AOC.
13.已知:如图,△ABC中,AC=12cm,AB=16cm,
(1)求AB边上的高CD;
(2)求△ABC的面积S;
(3)求tanB.
14.已知:如图,△ABC中,AB=9,BC=6,△ABC的面积等于9,求sinB.
拓展、探究、思考
15.已知:如图,Rt△ABC中,∠C=90°,按要求填空:
(1)∴______;
(2)∴b=______,c=______;
(3)∴a=______,b=______;
(4)∴______,______;
(5) ∴______,______;
(6)∵3,∴______,______.
课题:特殊锐角三角函数定义检测 (总课时20)
学习要求
1.掌握特殊角(30°,45°,60°)的正弦、余弦、正切三角函数值,会利用计算器求一个锐角的三角函数值以及由三角函数值求相应的锐角.
2.初步了解锐角三角函数的一些性质.
课堂学习检测
一、填空题
1.填表.
锐角 30° 45° 60°
sin
cos
tan
二、解答题
2.求下列各式的值.
(1) (2)tan30°-sin60°·sin30°
(3)cos45°+3tan30°+cos30°+2sin60°-2tan45°
(4)
3.求适合下列条件的锐角 .
(1) (2)
(3) (4)
综合、运用、诊断
4.已知:如图,在菱形ABCD中,DE⊥AB于E,BE=16cm,
求此菱形的周长.
5.已知:如图,在△ABC中,∠BAC=120°,AB=10,AC=5.
求:sin∠ACB的值.
6.已知:如图,Rt△ABC中,∠C=90°,∠BAC=30°,延长CA至D点,使AD=AB.求:
(1)∠D及∠DBC;
(2)tanD及tan∠DBC;
(3)请用类似的方法,求tan22.5°.
9.已知:如图,Rt△ABC中,∠C=90°,,作∠DAC=30°,AD交CB于D点,求:
(1)∠BAD;
(2)sin∠BAD、cos∠BAD和tan∠BAD.
10.已知:如图△ABC中,D为BC中点,且∠BAD=90°,,求:sin∠CAD、cos∠CAD、tan∠CAD.
拓展、探究、思考
11.已知:如图,∠AOB=90°,AO=OB,C、D是上的两点,∠AOD>∠AOC,求证:
(1)0<sin∠AOC<sin∠AOD<1;
(2)1>cos∠AOC>cos∠AOD>0;
(3)锐角的正弦函数值随角度的增大而______;
(4)锐角的余弦函数值随角度的增大而______.
12.已知:如图,CA⊥AO,E、F是AC上的两点,∠AOF>∠AOE.
(1)求证:tan∠AOF>tan∠AOE;
(2)锐角的21世纪教育网值随角度的增大而______.
13.已知:如图,Rt△ABC中,∠C=90°,求证:
(1)sin2A+cos2A=1;
(2)
课题:解直角三角形(一)检测 (总课时21)
学习要求
理解解直角三角形的意义,掌握解直角三角形的四种基本类型.
课堂学习检测
一、填空题
1.在解直角三角形的过程中,一般要用的主要关系如下(如图所示):
在Rt△ABC中,∠C=90°,AC=b,BC=a,AB=c,
第1题图
①三边之间的等量关系:
__________________________________.
②两锐角之间的关系:
__________________________________.
③边与角之间的关系:
______; _______;
_____; ______.
④直角三角形中成比例的线段(如图所示).
第④小题图
在Rt△ABC中,∠C=90°,CD⊥AB于D.
CD2=_________;AC2=_________;
BC2=_________;AC·BC=_________.
⑤直角三角形的主要线段(如图所示).
第⑤小题图
直角三角形斜边上的中线等于斜边的_________,斜边的中点是_________.
若r是Rt△ABC(∠C=90°)的内切圆半径,则r=_________=_________.
⑥直角三角形的面积公式.
在Rt△ABC中,∠C=90°,
S△ABC=_________.(答案不唯一)
2.关于直角三角形的可解条件,在直角三角形的六个元素中,除直角外,只要再知道_________(其中至少_________),这个三角形的形状、大小就可以确定下来.解直角三角形的基本类型可分为已知两条边(两条_________或斜边和_________)及已知一边和一个锐角(_________和一个锐角或_________和一个锐角)
3.填写下表:
已知条件 解法
一条边和 斜边c和锐角∠A ∠B=______,a=______,b=______
一个锐角 直角边a和锐角∠A ∠B=______,b=______,c=______
两条边 两条直角边a和b c=______,由______求∠A,∠B=______
直角边a和斜边c b=______,由______求∠A,∠B=______
二、解答题
4.在Rt△ABC中,∠C=90°.
(1)已知:a=35,,求∠A、∠B,b;
(2)已知:,,求∠A、∠B,c;
(3)已知:,,求a、b;
(4)已知:求a、c;
(5)已知:∠A=60°,△ABC的面积求a、b、c及∠B.
综合、运用、诊断
5.已知:如图,在半径为R的⊙O中,∠AOB=2 ,OC⊥AB于C点.
(1)求弦AB的长及弦心距;
(2)求⊙O的内接正n边形的边长an及边心距rn.
6.如图所示,图①中,一栋旧楼房由于防火设施较差,想要在侧面墙外修建一外部楼梯,由地面到二楼,再从二楼到三楼,共两段(图②中AB、BC两段),其中CC′=
BB′=3.2m.结合图中所给的信息,求两段楼梯AB与BC的长度之和(结果保留到0.1m).(参考数据:sin30°=0.50,cos30°≈0.87,sin35°≈0.57,cos35°≈0.82)
7.如图所示,某公司入口处原有三级台阶,每级台阶高为20cm,台阶面的宽为30cm,为了方便残疾人士,拟将台阶改为坡角为12°的斜坡,设原台阶的起点为A,斜坡的起点为C,求AC的长度(精确到1cm).
拓展、探究、思考
8.如图所示,甲楼在乙楼的西面,它们的设计高度是若干层,每层高均为3m,冬天太阳光与水平面的夹角为30°.
(1)若要求甲楼和乙楼的设计高度均为6层,且冬天甲楼的影子不能落在乙楼上,那么建筑时两楼之间的距离BD至少为多少米 (保留根号)
(2)由于受空间的限制,甲楼和乙楼的距离BD=21m,若仍要求冬天甲楼的影子不能落在乙楼上,那么设计甲楼时,最高应建几层
9.王英同学从A地沿北偏西60°方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地多少距离
10.已知:如图,在高2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要多少米 (保留整数)
课题:解直角三角形(二)检测 (总课时22)
能将解斜三角形的问题转化为解直角三角形.
课堂学习检测
1.已知:如图,△ABC中,∠A=30°,∠B=60°,AC=10cm.
求AB及BC的长.
2.已知:如图,Rt△ABC中,∠D=90°,∠B=45°,∠ACD=60°.BC=10cm.求AD的长.
3.已知:如图,△ABC中,∠A=30°,∠B=135°,AC=10cm.
求AB及BC的长.
4.已知:如图,Rt△ABC中,∠A=30°,∠C=90°,∠BDC=60°,BC=6cm.求AD的长.
综合、运用、诊断
5.已知:如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50m.现需从山顶A到河对岸点C拉一条笔直的缆绳AC,求山的高度及缆绳AC的长(答案可带根号).
6.已知:如图,一艘货轮向正北方向航行,在点A处测得灯塔M在北偏西30°,货轮以每小时20海里的速度航行,1小时后到达B处,测得灯塔M在北偏西45°,问该货轮继续向北航行时,与灯塔M之间的最短距离是多少 (精确到0.1海里,)
7.已知:如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°.点D到地面的垂直距离,求点B到地面的垂直距离BC.
8.已知:如图,小明准备测量学校旗杆AB的高度,当他发现斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,测得水平地面上的影长BC=20m,斜坡坡面上的影长CD=8m,太阳光线AD与水平地面成26°角,斜坡CD与水平地面所成的锐角为30°,求旗杆AB的高度(精确到1m).
9.已知:如图,在某旅游地一名游客由山脚A沿坡角为30°的山坡AB行走400m,到达一个景点B,再由B地沿山坡BC行走320米到达山顶C,如果在山顶C处观测到景点B的俯角为60°.求山高CD(精确到0.01米).
10.已知:如图,小明准备用如下方法测量路灯的高度:他走到路灯旁的一个地方,竖起一根2m长的竹竿,测得竹竿影长为1m,他沿着影子的方向,又向远处走出两根竹竿的长度,他又竖起竹竿,测得影长正好为2m.问路灯高度为多少米
11.已知:如图,在一次越野比赛中,运动员从营地A出发,沿北偏东60°方向走了500到达B点,然后再沿北偏西30°方向走了500m,到达目的地C点.求
(1)A、C两地之间的距离;
(2)确定目的地C在营地A的什么方向
12.已知:如图,在1998年特大洪水时期,要加固全长为10000m的河堤.大堤高5m,坝顶宽4m,迎水坡和背水坡都是坡度为1∶1的等腰梯形.现要将大堤加高1m,背水坡坡度改为1∶1.5.已知坝顶宽不变,求大坝横截面面积增加了多少平方米,完成工程需多少立方米的土石
E
O
A
B
C
D
·
E
O
A
B
C
D
·
【学习目标】
1经历当直角三角形的锐角固定时,它的对边与斜边的比值、邻边与斜边的比值都固定这一事实。
2 能根据正弦、余弦概念正确进行计算并掌握特殊三角函数值
【学习重点】
理解正弦、余弦(sinA、cosA)概念.
【学习难点】
理解正弦、余弦概念并熟记特殊三角函数值。
【导学过程】
一、自学提纲:
1、如图在Rt△ABC中,∠C=90°,∠A=30°,BC=10m,求AB、AC
2、如图在Rt△ABC中,∠C=90°,∠A=30°,AB=20m,求BC、AC
结论:直角三角形中,30°角的对边与斜边的比值
思考2:在Rt△ABC中,∠C=90°,∠A=45°,∠A对边与斜边
的比值是一个定值吗?如果是,是多少?
结论:直角三角形中,45°角的对边与斜边的比值
探究:任意画Rt△ABC和Rt△A′B′C′,使得∠C=∠C′=90°,
∠A=∠A′=a,那么有什么关系.你能解释一下吗?
结论:这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比
正弦函数概念:
规定:在Rt△BC中,∠C=90,∠A的对边记作a,∠B的对边记作b,∠C的对边记作c.
在Rt△BC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦,
记作sinA,即sinA= =. sinA=
∠A的邻边与斜边的比叫做∠A的余弦,记作cosA=,即cosA==
、例如,当∠A=30°时,我们有sinA=sin30°= ;
当∠A=45°时,我们有sinA=sin45°= .
计算 30° 45° 60°
siaA
cosA
四、学生展示:
例1 如图,在Rt△ABC中,
∠C=90°,求sinA和sinB的值.cosA和COSB的值
随堂练习
1.三角形在正方形网格纸中的位置如图所示,则sinα的值是﹙ ﹚
A.
B.
C.
D.
2.如图,在直角△ABC中,∠C=90o,若AB=5,AC=4,则sinA=( )
A. B. C. D.
3. 在△ABC中,∠C=90°,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
4.如图,已知点P的坐标是(a,b),则sinα等于( )
A. B. C.
课堂检测
1、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D。
已知AC=,BC=2,那么sin∠ACD=( )
A. B. C. D.
2、如图,已知AB是⊙O的直径,点C、D在⊙O上,
且AB=5,BC=3.则sin∠BAC= ;sin∠ADC= .
3. 在中,∠C=90°,如果cos A=那么的值为(?)
A.?B.?C.?D.
分析 本题主要考查锐解三角函数及三角变换知识。其思路是:依据条件
如图:P是∠的边OA上一点,且P点的坐标为(3,4),
则cosα=_____________.
课题:28.1锐角三角函数(总课时13)
【学习目标】
1: 感知当直角三角形的锐角固定时,它的邻边与斜边、对边与邻边的比值也都固定这一事实。
2:逐步培养学生观察、比较、分析、概括的思维能力。
重点:难点:
【学习重点】
理解余弦、正切的概念。
【学习难点】
熟练运用锐角三角函数的概念进行有关计算。
【导学过程】
一、自学提纲:
1、我们是怎样定义直角三角形中一个锐角的正弦的?
2、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D。
已知AC=,BC=2,那么sin∠ACD=( )
A. B. C. D.
3、如图,已知AB是⊙O的直径,点C、D在⊙O上,
且AB=5,BC=3.则sin∠BAC= ;sin∠ADC= .
4、在Rt△ABC中,∠C=90°,当锐角A确定时,
∠A的对边与斜边的比是 ,
现在我们要问:
∠A的邻边与斜边的比呢?
∠A的对边与邻边的比呢?
为什么?
二、合作交流:
探究:
一般地,当∠A取其他一定度数的锐角时,它的邻边与斜边的比是否也是一个固定值?
如图:Rt△ABC与Rt△A`B`C`,∠C=∠C` =90o,∠B=∠B`=α,
那么与有什么关系?
三、教师点拨:
类似于正弦的情况,
如图在Rt△BC中,∠C=90°,当锐角A的大小确定时,∠A的邻边与斜边的比、∠A的对边与邻边的比也分别是确定的.我们
把∠A的对边与邻边的比叫做∠A的正切,记作tanA,即tanA==.
例如,当∠A=30°时,我们有cosA=cos30°= ;
当∠A=45°时,我们有tanA=tan45°= .
(教师讲解并板书):锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,cosA,tanA也是A的函数.
例2:如图,在Rt△ABC中,∠C=90°,BC=6,sinA=,求cosA、tanB的值.
四、学生展示:
练习一:完成课本P81 练习1、2、3
练习二:
1.?在中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,则有(?)
A.?B.?C.?D.
本题主要考查锐解三角函数的定义,同学们只要依据
五、课堂小结:
在Rt△BC中,∠C=90°,我们把
锐角A的对边与斜边的比叫做∠A的正弦,
记作sinA,即sinA= =. sinA=
把∠A的邻边与斜边的比叫做∠A的余弦,
记作 ,即
把∠A的对边与邻边的比叫做∠A的正切,
记作 ,即
课题:28.1锐角三角函数(总课时14)
【学习目标】
⑴: 能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数。
⑵: 能熟练计算含有30°、45°、60°角的三角函数的运算式
【学习重点】
熟记30°、45°、60°角的三角函数值,能熟练计算含有30°、45°、60°角的三角函数的运算式
【学习难点】
30°、45°、60°角的三角函数值的推导过程
【导学过程】
一、自学提纲:
一个直角三角形中,
一个锐角正弦是怎么定义的?
一个锐角余弦是怎么定义的?
一个锐角正切是怎么定义的?
二、合作交流:
思考:
两块三角尺中有几个不同的锐角?
是多少度?
你能分别求出这几个锐角的正弦值、余弦值和正切值码?.
三、教师点拨:
归纳结果
30° 45° 60°
siaA
cosA
tanA
例3:求下列各式的值.
(1)cos260°+sin260°. (2)-tan45°.
例4:(1)如图(1),在Rt△ABC中,∠C=90,AB=,BC=,求∠A的度数.
(2)如图(2),已知圆锥的高AO等于圆锥的底面半径OB的倍,求a.
四、学生展示:
一、课本83页 第1 题
课本83页 第 2题
二、选择题.
1.已知:Rt△ABC中,∠C=90°,cosA=,AB=15,则AC的长是( ).
A.3 B.6 C.9 D.12
2.下列各式中不正确的是( ).
A.sin260°+cos260°=1 B.sin30°+cos30°=1
C.sin35°=cos55° D.tan45°>sin45°
3.计算2sin30°-2cos60°+tan45°的结果是( ).
A.2 B. C. D.1
4.已知∠A为锐角,且cosA≤,那么( )
A.0°<∠A≤60°B.60°≤∠A<90° C.0°<∠A≤30°D.30°≤∠A<90°
5.在△ABC中,∠A、∠B都是锐角,且sinA=,
cosB= eq \f(,2) ,则△ABC的形状是( )
A.直角三角形 B.钝角三角形C.锐角三角形 D.不能确定
6.如图Rt△ABC中,∠ACB=90°,CD⊥AB于D,BC=3,AC=4,设∠BCD=a,则tana的值为( ).
A. B. C. D.
7.当锐角a>60°时,cosa的值( ).
A.小于 B.大于 C.大于 eq \f(,2) D.大于1
8.在△ABC中,三边之比为a:b:c=1::2,则sinA+tanA等于( ).
A.
9.已知梯形ABCD中,腰BC长为2,梯形对角线BD垂直平分AC,若梯形的高是,则∠CAB等于( )
A.30° B.60° C.45° D.以上都不对
10.sin272°+sin218°的值是( ).
A.1 B.0 C. D. eq \f(,2)
11.若(tanA-3)2+│2cosB-│=0,则△ABC( ).
A.是直角三角形 B.是等边三角形
C.是含有60°的任意三角形 D.是顶角为钝角的等腰三角形
三、填空题.
12.设α、β均为锐角,且sinα-cosβ=0,则α+β=_______.
13.的值是_______.
14.已知,等腰△ABC的腰长为4,底为30°,则底边上的高为______,周长为______.
15.在Rt△ABC中,∠C=90°,已知tanB= eq \f(,2) ,则cosA=________.
五、课堂小结:要牢记下表:
30° 45° 60°
siaA
cosA
tanA
六、作业设置:
课本 第85页 习题28.1复习巩固第3题
七、自我反思:
本节课我的收获: 。
课题:28.1锐角三角函数(总课时15)
【学习目标】
让学生熟识计算器一些功能键的使用
【学习重点】
运用计算器处理三角函数中的值或角的问题
【学习难点】
知道值求角的处理
【导学过程】
求下列各式的值.
(1)sin30°·cos45°+cos60°; (2)2sin60°-2cos30°·sin45°
(3); (4)-sin60°(1-sin30°).
(5)tan45°·sin60°-4sin30°·cos45°+·tan30°
(6)+cos45°·cos30°
合作交流:
学生去完成课本83 84页
学生展示:
用计算器求锐角的正弦、余弦、正切值
学生去完成课本83 86页的题目
自我反思:
本节课我的收获: 。
课题:28.2解直角三角形(1)(总课时16)
【学习目标】
1: 使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形
2: 通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.
3: 渗透数形结合的数学思想,培养学生良好的学习习惯.
【学习重点】
直角三角形的解法.
【学习难点】
三角函数在解直角三角形中的灵活运用
【导学过程】
一、自学提纲:
1.在三角形中共有几个元素?
2.直角三角形ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
(1)边角之间关系
如果用表示直角三角形的一个锐角,那上述式子就可以写成.
(2)三边之间关系 (3)锐角之间关系∠A+∠B=90°.
a2 +b2 =c2 (勾股定理) 以上三点正是解直角三角形的依据.
二、合作交流:
要想使人安全地攀上斜靠在墙面上的梯子的顶端.梯子与地面所成的角一般要满足, (如图).现有一个长6m的梯子,问:
(1)使用这个梯子最高可以安全攀上多高的墙(精确到0. 1 m)
(2)当梯子底端距离墙面2.4 m时,梯子与地面所成的角等于多少(精确到1o) 这时人是否能够安全使用这个梯子
三、教师点拨:
例1在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且b=,
a=,解这个三角形.
例2在Rt△ABC中, ∠B =35o,b=20,解这个三角形.
四、学生展示:
完成课本91页练习
补充题
1.根据直角三角形的__________元素(至少有一个边),求出________其它所有元素的过程,即解直角三角形.
2、在Rt△ABC中,a=104.0,b=20.49,解这个三角形.
3、 在△ABC中,∠C为直角,AC=6,的平分线AD=4,解此直角三角形。
4、Rt△ABC中,若sinA=,AB=10,那么BC=_____,tanB=______.
5、在△ABC中,∠C=90°,AC=6,BC=8,那么sinA=________.
6、在△ABC中,∠C=90°,sinA=,则cosA的值是( )
A. B. C.
五、课堂小结:
小结“已知一边一角,如何解直角三角形?”
六、作业设置:
课本 第96页 习题28.2复习巩固第1题、第2题.
七、自我反思:
本节课我的收获: 。
课题:28.2解直角三角形(2)(总课时17)
【学习目标】
⑴: 使学生了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.
⑵: 逐步培养学生分析问题、解决问题的能力.
⑶: 渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识
【学习重点】
将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.
【学习难点】
实际问题转化成数学模型
【导学过程】
一、自学提纲:
1.解直角三角形指什么?
2.解直角三角形主要依据什么?
(1)勾股定理:
(2)锐角之间的关系:
(3)边角之间的关系:
tanA=
二、合作交流:
仰角、俯角
当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.
三、教师点拨:
例3 2003年10月15日“神舟”5号载人航天飞船发射成功.当飞船完成变轨后,就在离地球表面350km的圆形轨道上运行.如图,当飞船运行到地球表面上P点的正上方时,从飞船上最远能直接看到的地球上的点在什么位置 这样的最远点与P点的距离是多少 (地球半径约为6 400 km,结果精确到0. 1 km)
例4热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30o,看这栋离楼底部的俯角为60o,热气球与高楼的水平距离为120 m.这栋高楼有多高(结果精确到0.1m)
四、学生展示:
一、课本93页 练习 第1 、2题
五、课堂小结:
六、作业设置:
课本 第96页 习题28.2复习巩固第3、4题
七、自我反思:
本节课我的收获: 。
课题:28.2解直角三角形(3)(总课时18)
【学习目标】
⑴: 使学生了解方位角的命名特点,能准确把握所指的方位角是指哪一个角
⑵: 逐步培养学生分析问题、解决问题的能力;渗透数形结合的数学思想和方法.
⑶: 巩固用三角函数有关知识解决问题,学会解决方位角问题.
【学习重点】
用三角函数有关知识解决方位角问题
【学习难点】
学会准确分析问题并将实际问题转化成数学模型
【导学过程】
一、自学提纲:
坡度与坡角
坡面的铅直高度h和水平宽度的比叫做坡度(或叫做坡比),
一般用i表示。即i=,常写成i=1:m的形式如i=1:2.5
把坡面与水平面的夹角α叫做坡角.
结合图形思考,坡度i与坡角α之间具有什么关系?
这一关系在实际问题中经常用到。
二、教师点拨:
例5如图,一艘海轮位于灯塔P的北偏东65方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34方向上的B处.这时,海轮所在的B处距离灯塔P有多远?
例6同学们,如果你是修建三峡大坝的工程师,现在有这样一个问题请你解决:如图6-33
水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求斜坡AB的坡面角α,坝底宽AD和斜坡AB的长(精确到0.1m)
四、学生展示:
完成课本91页练习
补充练习
(1)一段坡面的坡角为60°,则坡度i=______;
______,
坡角______度.
2、利用土埂修筑一条渠道,在埂中间挖去深为0.6米的一块(图阴影部分是挖去部分),已知渠道内坡度为1∶1.5,渠道底面宽BC为0.5米,求:
①横断面(等腰梯形)ABCD的面积;
②修一条长为100米的渠道要挖去的土方数.
五、课堂小结:
六、作业设置:
课本 第96页 习题28.2复习巩固第5、6、7题
七、自我反思:
本节课我的收获: 。
课题:锐角三角函数定义检测 (总课时19)
学习要求
理解一个锐角的正弦、余弦、正切的定义.能依据锐角三角函数的定义,求给定锐角的三角函数值.
课堂学习检测
一、填空题
1.如图所示,B、B′是∠MAN的AN边上的任意两点,BC⊥AM于C点,B′C′⊥AM于C′点,则△B'AC′∽______,从而,又可得
①______,即在Rt△ABC中(∠C=90°),当∠A确定时,它的______与______的比是一个______值;
②______,即在Rt△ABC中(∠C=90°),当∠A确定时,它的______与______的比也是一个______;
③______,即在Rt△ABC中(∠C=90°),当∠A确定时,它的______与______的比还是一个______.
第1题图
2.如图所示,在Rt△ABC中,∠C=90°.
第2题图
①=______, =______;
②=______, =______;
③=______, =______.
3.因为对于锐角 的每一个确定的值,sin 、cos 、tan 分别都有____________与它______,所以sin 、cos 、tan 都是____________.又称为 的____________.
4.在Rt△ABC中,∠C=90°,若a=9,b=12,则c=______,
sinA=______,cosA=______,tanA=______,
sinB=______,cosB=______,tanB=______.
5.在Rt△ABC中,∠C=90°,若a=1,b=3,则c=______,
sinA=______,cosA=______,tanA=______,
sinB=______,cosB=______,tanB=______.
6.在Rt△ABC中,∠B=90°,若a=16,c=30,则b=______,
sinA=______,cosA=______,tanA=______,
sinC=______,cosC=______,tanC=______.
7.在Rt△ABC中,∠C=90°,若∠A=30°,则∠B=______,
sinA=______,cosA=______,tanA=______,
sinB=______,cosB=______,tanB=______.
二、解答题
8.已知:如图,Rt△TNM中,∠TMN=90°,MR⊥TN于R点,TN=4,MN=3.
求:sin∠TMR、cos∠TMR、tan∠TMR.
9.已知Rt△ABC中,求AC、AB和cosB.
综合、运用、诊断
10.已知:如图,Rt△ABC中,∠C=90°.D是AC边上一点,DE⊥AB于E点.
DE∶AE=1∶2.
求:sinB、cosB、tanB.
11.已知:如图,⊙O的半径OA=16cm,OC⊥AB于C点,
求:AB及OC的长.
12.已知:⊙O中,OC⊥AB于C点,AB=16cm,
(1)求⊙O的半径OA的长及弦心距OC;
(2)求cos∠AOC及tan∠AOC.
13.已知:如图,△ABC中,AC=12cm,AB=16cm,
(1)求AB边上的高CD;
(2)求△ABC的面积S;
(3)求tanB.
14.已知:如图,△ABC中,AB=9,BC=6,△ABC的面积等于9,求sinB.
拓展、探究、思考
15.已知:如图,Rt△ABC中,∠C=90°,按要求填空:
(1)∴______;
(2)∴b=______,c=______;
(3)∴a=______,b=______;
(4)∴______,______;
(5) ∴______,______;
(6)∵3,∴______,______.
课题:特殊锐角三角函数定义检测 (总课时20)
学习要求
1.掌握特殊角(30°,45°,60°)的正弦、余弦、正切三角函数值,会利用计算器求一个锐角的三角函数值以及由三角函数值求相应的锐角.
2.初步了解锐角三角函数的一些性质.
课堂学习检测
一、填空题
1.填表.
锐角 30° 45° 60°
sin
cos
tan
二、解答题
2.求下列各式的值.
(1) (2)tan30°-sin60°·sin30°
(3)cos45°+3tan30°+cos30°+2sin60°-2tan45°
(4)
3.求适合下列条件的锐角 .
(1) (2)
(3) (4)
综合、运用、诊断
4.已知:如图,在菱形ABCD中,DE⊥AB于E,BE=16cm,
求此菱形的周长.
5.已知:如图,在△ABC中,∠BAC=120°,AB=10,AC=5.
求:sin∠ACB的值.
6.已知:如图,Rt△ABC中,∠C=90°,∠BAC=30°,延长CA至D点,使AD=AB.求:
(1)∠D及∠DBC;
(2)tanD及tan∠DBC;
(3)请用类似的方法,求tan22.5°.
9.已知:如图,Rt△ABC中,∠C=90°,,作∠DAC=30°,AD交CB于D点,求:
(1)∠BAD;
(2)sin∠BAD、cos∠BAD和tan∠BAD.
10.已知:如图△ABC中,D为BC中点,且∠BAD=90°,,求:sin∠CAD、cos∠CAD、tan∠CAD.
拓展、探究、思考
11.已知:如图,∠AOB=90°,AO=OB,C、D是上的两点,∠AOD>∠AOC,求证:
(1)0<sin∠AOC<sin∠AOD<1;
(2)1>cos∠AOC>cos∠AOD>0;
(3)锐角的正弦函数值随角度的增大而______;
(4)锐角的余弦函数值随角度的增大而______.
12.已知:如图,CA⊥AO,E、F是AC上的两点,∠AOF>∠AOE.
(1)求证:tan∠AOF>tan∠AOE;
(2)锐角的21世纪教育网值随角度的增大而______.
13.已知:如图,Rt△ABC中,∠C=90°,求证:
(1)sin2A+cos2A=1;
(2)
课题:解直角三角形(一)检测 (总课时21)
学习要求
理解解直角三角形的意义,掌握解直角三角形的四种基本类型.
课堂学习检测
一、填空题
1.在解直角三角形的过程中,一般要用的主要关系如下(如图所示):
在Rt△ABC中,∠C=90°,AC=b,BC=a,AB=c,
第1题图
①三边之间的等量关系:
__________________________________.
②两锐角之间的关系:
__________________________________.
③边与角之间的关系:
______; _______;
_____; ______.
④直角三角形中成比例的线段(如图所示).
第④小题图
在Rt△ABC中,∠C=90°,CD⊥AB于D.
CD2=_________;AC2=_________;
BC2=_________;AC·BC=_________.
⑤直角三角形的主要线段(如图所示).
第⑤小题图
直角三角形斜边上的中线等于斜边的_________,斜边的中点是_________.
若r是Rt△ABC(∠C=90°)的内切圆半径,则r=_________=_________.
⑥直角三角形的面积公式.
在Rt△ABC中,∠C=90°,
S△ABC=_________.(答案不唯一)
2.关于直角三角形的可解条件,在直角三角形的六个元素中,除直角外,只要再知道_________(其中至少_________),这个三角形的形状、大小就可以确定下来.解直角三角形的基本类型可分为已知两条边(两条_________或斜边和_________)及已知一边和一个锐角(_________和一个锐角或_________和一个锐角)
3.填写下表:
已知条件 解法
一条边和 斜边c和锐角∠A ∠B=______,a=______,b=______
一个锐角 直角边a和锐角∠A ∠B=______,b=______,c=______
两条边 两条直角边a和b c=______,由______求∠A,∠B=______
直角边a和斜边c b=______,由______求∠A,∠B=______
二、解答题
4.在Rt△ABC中,∠C=90°.
(1)已知:a=35,,求∠A、∠B,b;
(2)已知:,,求∠A、∠B,c;
(3)已知:,,求a、b;
(4)已知:求a、c;
(5)已知:∠A=60°,△ABC的面积求a、b、c及∠B.
综合、运用、诊断
5.已知:如图,在半径为R的⊙O中,∠AOB=2 ,OC⊥AB于C点.
(1)求弦AB的长及弦心距;
(2)求⊙O的内接正n边形的边长an及边心距rn.
6.如图所示,图①中,一栋旧楼房由于防火设施较差,想要在侧面墙外修建一外部楼梯,由地面到二楼,再从二楼到三楼,共两段(图②中AB、BC两段),其中CC′=
BB′=3.2m.结合图中所给的信息,求两段楼梯AB与BC的长度之和(结果保留到0.1m).(参考数据:sin30°=0.50,cos30°≈0.87,sin35°≈0.57,cos35°≈0.82)
7.如图所示,某公司入口处原有三级台阶,每级台阶高为20cm,台阶面的宽为30cm,为了方便残疾人士,拟将台阶改为坡角为12°的斜坡,设原台阶的起点为A,斜坡的起点为C,求AC的长度(精确到1cm).
拓展、探究、思考
8.如图所示,甲楼在乙楼的西面,它们的设计高度是若干层,每层高均为3m,冬天太阳光与水平面的夹角为30°.
(1)若要求甲楼和乙楼的设计高度均为6层,且冬天甲楼的影子不能落在乙楼上,那么建筑时两楼之间的距离BD至少为多少米 (保留根号)
(2)由于受空间的限制,甲楼和乙楼的距离BD=21m,若仍要求冬天甲楼的影子不能落在乙楼上,那么设计甲楼时,最高应建几层
9.王英同学从A地沿北偏西60°方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地多少距离
10.已知:如图,在高2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要多少米 (保留整数)
课题:解直角三角形(二)检测 (总课时22)
能将解斜三角形的问题转化为解直角三角形.
课堂学习检测
1.已知:如图,△ABC中,∠A=30°,∠B=60°,AC=10cm.
求AB及BC的长.
2.已知:如图,Rt△ABC中,∠D=90°,∠B=45°,∠ACD=60°.BC=10cm.求AD的长.
3.已知:如图,△ABC中,∠A=30°,∠B=135°,AC=10cm.
求AB及BC的长.
4.已知:如图,Rt△ABC中,∠A=30°,∠C=90°,∠BDC=60°,BC=6cm.求AD的长.
综合、运用、诊断
5.已知:如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50m.现需从山顶A到河对岸点C拉一条笔直的缆绳AC,求山的高度及缆绳AC的长(答案可带根号).
6.已知:如图,一艘货轮向正北方向航行,在点A处测得灯塔M在北偏西30°,货轮以每小时20海里的速度航行,1小时后到达B处,测得灯塔M在北偏西45°,问该货轮继续向北航行时,与灯塔M之间的最短距离是多少 (精确到0.1海里,)
7.已知:如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°.点D到地面的垂直距离,求点B到地面的垂直距离BC.
8.已知:如图,小明准备测量学校旗杆AB的高度,当他发现斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,测得水平地面上的影长BC=20m,斜坡坡面上的影长CD=8m,太阳光线AD与水平地面成26°角,斜坡CD与水平地面所成的锐角为30°,求旗杆AB的高度(精确到1m).
9.已知:如图,在某旅游地一名游客由山脚A沿坡角为30°的山坡AB行走400m,到达一个景点B,再由B地沿山坡BC行走320米到达山顶C,如果在山顶C处观测到景点B的俯角为60°.求山高CD(精确到0.01米).
10.已知:如图,小明准备用如下方法测量路灯的高度:他走到路灯旁的一个地方,竖起一根2m长的竹竿,测得竹竿影长为1m,他沿着影子的方向,又向远处走出两根竹竿的长度,他又竖起竹竿,测得影长正好为2m.问路灯高度为多少米
11.已知:如图,在一次越野比赛中,运动员从营地A出发,沿北偏东60°方向走了500到达B点,然后再沿北偏西30°方向走了500m,到达目的地C点.求
(1)A、C两地之间的距离;
(2)确定目的地C在营地A的什么方向
12.已知:如图,在1998年特大洪水时期,要加固全长为10000m的河堤.大堤高5m,坝顶宽4m,迎水坡和背水坡都是坡度为1∶1的等腰梯形.现要将大堤加高1m,背水坡坡度改为1∶1.5.已知坝顶宽不变,求大坝横截面面积增加了多少平方米,完成工程需多少立方米的土石
E
O
A
B
C
D
·
E
O
A
B
C
D
·
