【新课标】24.4.1直线与圆的位置关系及切线的判定与性质 课件(共40张PPT)
文档属性
| 名称 | 【新课标】24.4.1直线与圆的位置关系及切线的判定与性质 课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-07 00:00:00 | ||
图片预览









文档简介
(共40张PPT)
24.4.1直线与圆的位置关系及切线的性质
沪科版 九年级下
教学内容分析
本节在学习了圆的基本概念之后,利用点到直线的距离d与半径r来研究直线与圆的三种位置关系,又学习了切线的性质,与下一节的切线长也有密切联系,具有承上启下的作用。
教学目标
1.运用点到直线的距离d与半径r,来判定直线与圆的三种位置关系;(重点)
2.利用切线的性质解决实际问题;(难点)
3.学会经过一个点作圆的切线。
核心素养分析
本节学习了用点到直线的距离d与半径r来研究直线与圆的三种位置关系,又学习了运用切线的性质进行计算,锻炼了学生的计算能力,培养了学生严谨的推理能力。
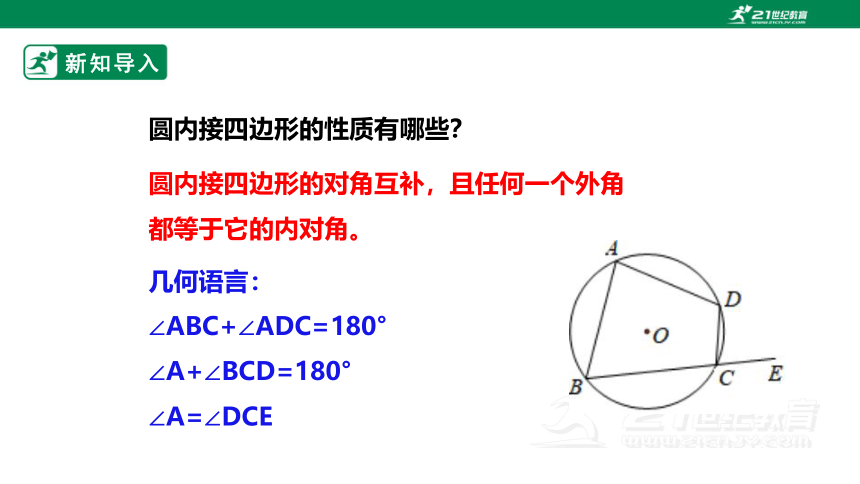
圆内接四边形的对角互补,且任何一个外角都等于它的内对角。
几何语言:
∠ABC+∠ADC=180°
∠A+∠BCD=180°
∠A=∠DCE
圆内接四边形的性质有哪些?
新知导入
新知讲解
1.日出的一组照片反映了太阳与地平线的位置变化,将照片中太阳与地平线(图24-40)分别看作圆与直线,并按它们之间不同的位置关系表示成如图24-41.
观察
图24-40
新知讲解
2.在图24-41 中,观察⊙O与直线l的公共点的个数,有几种情况?
O
l
(2)
O
l
(1)
O
(3)
l
图24-41
新知讲解
如果直线与圆有两个公共点,这时直线与圆的位置关系叫做相交,这条直线叫做圆的割线。
O
l
(1)
割线
新知讲解
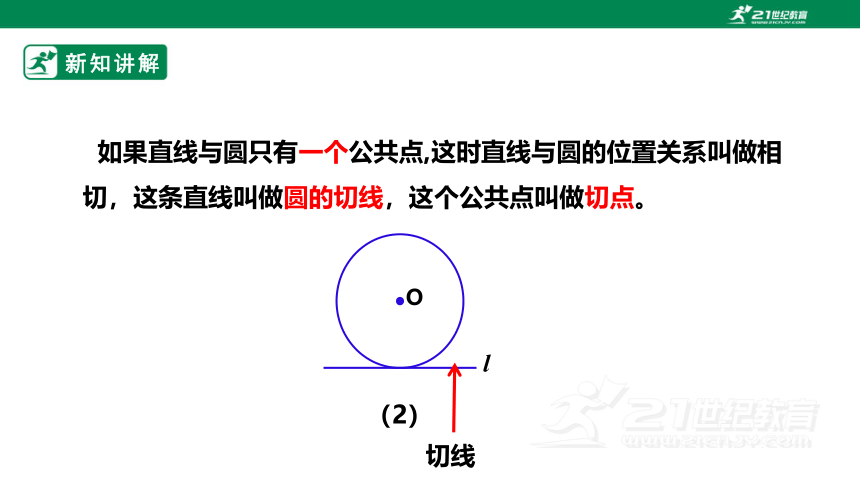
如果直线与圆只有一个公共点,这时直线与圆的位置关系叫做相切,这条直线叫做圆的切线,这个公共点叫做切点。
O
l
(2)
切线
新知讲解
如果直线与圆没有公共点,这时直线与圆的位置关系叫做相离.
O
l
(3)
新知讲解
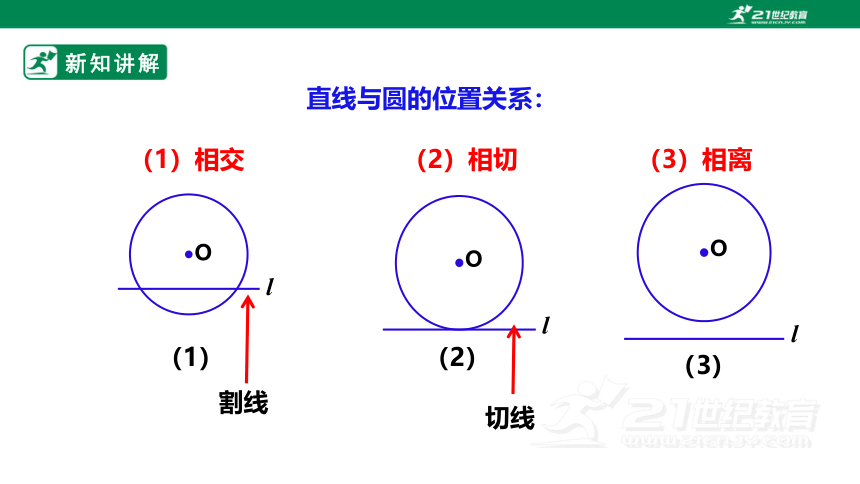
直线与圆的位置关系:
O
l
(1)
割线
O
l
(2)
切线
O
l
(3)
(1)相交
(2)相切
(3)相离
变式 如图,两个同心圆的半径分别为3,5,直线l与大⊙O交于点A,B,若AB=6 ,则直线l与小⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
新知讲解
新知讲解
解:如图,作OH⊥AB于H
∵OH⊥AB,
∴AH=BH=3,
在Rt△AOH中,
OH = =4 ,
∵4>3,
∴直线AB与⊙O相离
故选:C
设⊙O的半径为r,圆心О到直线I的距离为d,由上述直线与圆的位置关系可知:
(1)直线I与⊙O相交 d新知讲解
O
l
(1)
d
新知讲解
(2)直线I与⊙O相切 d =r ;
O
l
(2)
d
新知讲解
(3)直线I与⊙O相离 d >r.
O
l
(3)
d
-
-
新知讲解
O
l
(1)
d
O
l
(2)
d
O
l
(3)
d
-
-
直线I与⊙O相交 d直线I与⊙O相切 d=r
直线I与⊙O相离 d>r
直线与圆的位置关系(d与r的关系)
小结:判断直线与圆的位置关系时,通常要得到圆心到直线的距离d和圆的半径r,然后再利用d与r的大小关系进行判断.
直线与圆的位置关系:
①当d>r时,直线与圆相离;
②当d=r时, 直线与圆相切;
③当d<r时,直线与圆相交.
新知讲解
新知讲解
如图,当直线I与⊙O相切时,切点为A,连接OA、这时,如在直线l上任取一个不同于点A的点P,连接OP ,比较OA和OP的大小?
O
l
(2)
A
P
-
-
新知讲解
因为点P在⊙O外,所以OP>OA。
OA是点О到直线l上任一点的连线中最短的,故OA⊥l。
O
l
(2)
A
P
-
-
新知讲解
切线性质
圆的切线垂直于经过切点的半径.
O
l
(2)
如图,l是⊙O的切线,OA为半径,
∴OA⊥l
A
-
-
新知讲解
变式 如图,从⊙O外一点P引圆的两条切线PA,PB,切点分别是A,B,若∠APB=60°,PA=5,则弦AB的长是( )
A. 4 B. 6 C. 5 D. 7
C
新知讲解
解:∵PA,PB为⊙O的两条切线,
∴PA=PB,
∵∠APB=60°,
∴△PAB为等边三角形,
∴AB=PA=5,
故选C.
新知讲解
例1 如图,Rt△ABC的斜边AB =10cm,∠A =30°.
(1)以点C为圆心作圆,当半径为多少时,AB 与⊙C相切
(2)以点C为圆心.半径r分别为4 cm和 5 cm作两个圆,这两个圆与斜边AB分别有怎样的位置关系
C
A
B
新知讲解
解:(1)过点C作边AB上的高CD.
∵∠A =30°,AB =10 cm,
∴BC= AB= ×10 =5(cm).
在Rt△BCD中,有CD=BCsinB=5sin60°= ( cm ).
当半径为 cm时,AB与⊙C相切.
-
-
C
A
B
D
新知讲解
(2)由(1)可知,圆心C到AB的距离 cm.
当r=4 cm时,d>r,⊙C与AB相离;
当r=5 cm时,d-
-
C
A
B
D
新知讲解
思考
1.如图,经过圆上一点P,作直线与已知圆相切,如何作 能够作几条
.O
P
.
过圆上一点能够作1条直线与已知圆相切
新知讲解
2.如图,经过圆外一点P,作直线与已知圆相切,如何作 能够作几条
.O
.P
过圆外一点能够作2条直线与已知圆相切
1.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,以C为圆心,4为半径的圆与AB的位置关系为_________________.
课堂练习
相离
B
A
C
解:过C点作CD⊥AB,垂足为D,
∵∠ACB=90°,BC=8,AC=6,
由勾股定理,得AB= ,
根据三角形计算面积的方法可知,
BC×AC=AB×CD,
∴CD=(6×8)÷10=4.8>4,
∴⊙C与直线AB相离.
课堂练习
B
A
C
D
课堂练习
2.如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,点P在边AC上,⊙P的半径为1.如果⊙P与边BC和边AB都没有公共点,那么线段PC长的取值范围是___________.
课堂练习
解:在Rt△ABC中,∠ACB=90°,AB=5,BC=3,
∴AC=4,
当⊙P与AB相切时,设切点为D,如图,
连接PD,
则PD⊥AB,
∴∠C=∠ADP=90°,
课堂练习
∵∠A=∠A,
∴△ADP∽△ACB,
∴
∴ ,
∴ ,
∴PC=AC-PA= ,
∴线段PC长的取值范围是
课堂练习
3.如图,⊙O与正五边形ABCDE的边AB,DE分别相切于点B,D,则劣弧BD所对的圆心角∠BOD的大小为( )
A. 108° B. 118° C. 144° D. 120°
C
课堂练习
解:∵五边形ABCDE是正五边形,
∴∠E=∠A=540°÷5=108°.
∵AB、DE与⊙O相切,
∴∠OBA=∠ODE=90°,
∴∠BOD=(5-2)×180°-90°-108°-108°-90°=144°,
故选:C.
课堂总结
直线与圆的位置关系有3种:
(1)直线l和⊙O相交 d<r;
(2)直线l和⊙O相切 d=r;
(3)直线l和⊙O相离 d>r.
切线性质
圆的切线垂直于经过切点的半径.
板书设计
24.4.1直线与圆的位置关系及切线的性质
1.直线与圆的位置关系
2.切线性质
作业布置
必做题:课本P36的第1~3题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
24.4.1直线与圆的位置关系及切线的性质
沪科版 九年级下
教学内容分析
本节在学习了圆的基本概念之后,利用点到直线的距离d与半径r来研究直线与圆的三种位置关系,又学习了切线的性质,与下一节的切线长也有密切联系,具有承上启下的作用。
教学目标
1.运用点到直线的距离d与半径r,来判定直线与圆的三种位置关系;(重点)
2.利用切线的性质解决实际问题;(难点)
3.学会经过一个点作圆的切线。
核心素养分析
本节学习了用点到直线的距离d与半径r来研究直线与圆的三种位置关系,又学习了运用切线的性质进行计算,锻炼了学生的计算能力,培养了学生严谨的推理能力。
圆内接四边形的对角互补,且任何一个外角都等于它的内对角。
几何语言:
∠ABC+∠ADC=180°
∠A+∠BCD=180°
∠A=∠DCE
圆内接四边形的性质有哪些?
新知导入
新知讲解
1.日出的一组照片反映了太阳与地平线的位置变化,将照片中太阳与地平线(图24-40)分别看作圆与直线,并按它们之间不同的位置关系表示成如图24-41.
观察
图24-40
新知讲解
2.在图24-41 中,观察⊙O与直线l的公共点的个数,有几种情况?
O
l
(2)
O
l
(1)
O
(3)
l
图24-41
新知讲解
如果直线与圆有两个公共点,这时直线与圆的位置关系叫做相交,这条直线叫做圆的割线。
O
l
(1)
割线
新知讲解
如果直线与圆只有一个公共点,这时直线与圆的位置关系叫做相切,这条直线叫做圆的切线,这个公共点叫做切点。
O
l
(2)
切线
新知讲解
如果直线与圆没有公共点,这时直线与圆的位置关系叫做相离.
O
l
(3)
新知讲解
直线与圆的位置关系:
O
l
(1)
割线
O
l
(2)
切线
O
l
(3)
(1)相交
(2)相切
(3)相离
变式 如图,两个同心圆的半径分别为3,5,直线l与大⊙O交于点A,B,若AB=6 ,则直线l与小⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
新知讲解
新知讲解
解:如图,作OH⊥AB于H
∵OH⊥AB,
∴AH=BH=3,
在Rt△AOH中,
OH = =4 ,
∵4>3,
∴直线AB与⊙O相离
故选:C
设⊙O的半径为r,圆心О到直线I的距离为d,由上述直线与圆的位置关系可知:
(1)直线I与⊙O相交 d
O
l
(1)
d
新知讲解
(2)直线I与⊙O相切 d =r ;
O
l
(2)
d
新知讲解
(3)直线I与⊙O相离 d >r.
O
l
(3)
d
-
-
新知讲解
O
l
(1)
d
O
l
(2)
d
O
l
(3)
d
-
-
直线I与⊙O相交 d
直线I与⊙O相离 d>r
直线与圆的位置关系(d与r的关系)
小结:判断直线与圆的位置关系时,通常要得到圆心到直线的距离d和圆的半径r,然后再利用d与r的大小关系进行判断.
直线与圆的位置关系:
①当d>r时,直线与圆相离;
②当d=r时, 直线与圆相切;
③当d<r时,直线与圆相交.
新知讲解
新知讲解
如图,当直线I与⊙O相切时,切点为A,连接OA、这时,如在直线l上任取一个不同于点A的点P,连接OP ,比较OA和OP的大小?
O
l
(2)
A
P
-
-
新知讲解
因为点P在⊙O外,所以OP>OA。
OA是点О到直线l上任一点的连线中最短的,故OA⊥l。
O
l
(2)
A
P
-
-
新知讲解
切线性质
圆的切线垂直于经过切点的半径.
O
l
(2)
如图,l是⊙O的切线,OA为半径,
∴OA⊥l
A
-
-
新知讲解
变式 如图,从⊙O外一点P引圆的两条切线PA,PB,切点分别是A,B,若∠APB=60°,PA=5,则弦AB的长是( )
A. 4 B. 6 C. 5 D. 7
C
新知讲解
解:∵PA,PB为⊙O的两条切线,
∴PA=PB,
∵∠APB=60°,
∴△PAB为等边三角形,
∴AB=PA=5,
故选C.
新知讲解
例1 如图,Rt△ABC的斜边AB =10cm,∠A =30°.
(1)以点C为圆心作圆,当半径为多少时,AB 与⊙C相切
(2)以点C为圆心.半径r分别为4 cm和 5 cm作两个圆,这两个圆与斜边AB分别有怎样的位置关系
C
A
B
新知讲解
解:(1)过点C作边AB上的高CD.
∵∠A =30°,AB =10 cm,
∴BC= AB= ×10 =5(cm).
在Rt△BCD中,有CD=BCsinB=5sin60°= ( cm ).
当半径为 cm时,AB与⊙C相切.
-
-
C
A
B
D
新知讲解
(2)由(1)可知,圆心C到AB的距离 cm.
当r=4 cm时,d>r,⊙C与AB相离;
当r=5 cm时,d
-
C
A
B
D
新知讲解
思考
1.如图,经过圆上一点P,作直线与已知圆相切,如何作 能够作几条
.O
P
.
过圆上一点能够作1条直线与已知圆相切
新知讲解
2.如图,经过圆外一点P,作直线与已知圆相切,如何作 能够作几条
.O
.P
过圆外一点能够作2条直线与已知圆相切
1.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,以C为圆心,4为半径的圆与AB的位置关系为_________________.
课堂练习
相离
B
A
C
解:过C点作CD⊥AB,垂足为D,
∵∠ACB=90°,BC=8,AC=6,
由勾股定理,得AB= ,
根据三角形计算面积的方法可知,
BC×AC=AB×CD,
∴CD=(6×8)÷10=4.8>4,
∴⊙C与直线AB相离.
课堂练习
B
A
C
D
课堂练习
2.如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,点P在边AC上,⊙P的半径为1.如果⊙P与边BC和边AB都没有公共点,那么线段PC长的取值范围是___________.
课堂练习
解:在Rt△ABC中,∠ACB=90°,AB=5,BC=3,
∴AC=4,
当⊙P与AB相切时,设切点为D,如图,
连接PD,
则PD⊥AB,
∴∠C=∠ADP=90°,
课堂练习
∵∠A=∠A,
∴△ADP∽△ACB,
∴
∴ ,
∴ ,
∴PC=AC-PA= ,
∴线段PC长的取值范围是
课堂练习
3.如图,⊙O与正五边形ABCDE的边AB,DE分别相切于点B,D,则劣弧BD所对的圆心角∠BOD的大小为( )
A. 108° B. 118° C. 144° D. 120°
C
课堂练习
解:∵五边形ABCDE是正五边形,
∴∠E=∠A=540°÷5=108°.
∵AB、DE与⊙O相切,
∴∠OBA=∠ODE=90°,
∴∠BOD=(5-2)×180°-90°-108°-108°-90°=144°,
故选:C.
课堂总结
直线与圆的位置关系有3种:
(1)直线l和⊙O相交 d<r;
(2)直线l和⊙O相切 d=r;
(3)直线l和⊙O相离 d>r.
切线性质
圆的切线垂直于经过切点的半径.
板书设计
24.4.1直线与圆的位置关系及切线的性质
1.直线与圆的位置关系
2.切线性质
作业布置
必做题:课本P36的第1~3题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
