【核心素养目标】24.5三角形的内切圆 教学设计
文档属性
| 名称 | 【核心素养目标】24.5三角形的内切圆 教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 09:01:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
沪科版九年级下册数学24.5三角形的内切圆 教学设计
课题 24.5三角形的内切圆 单元 第24单元 学科 数学 年级 九
教材分析 前面学习了圆的切线的性质和判定,本节在此基础上,研究了三角形内切圆的问题,首先理解三角形的内切圆、三角形的内心等概念;还学习了作出一个三角形的内切圆,并利用内心的概念来求角、边等综合问题。
核心素养分析 本节重点研究了三角形的内切圆,学会作出一个三角形的内切圆,锻炼了学生的动手操作能力,还有利用内切圆求角、边等综合问题,培养了学生的计算能力和推理能力。
学习目标 1.理解三角形的内切圆概念;2.作出三角形的内切圆,理解三角形的内切圆的步骤;3.能根据三角形的内切圆求与内切圆相关的问题。
重点 作出三角形的内切圆,理解三角形的内切圆的步骤。
难点 能根据三角形的内切圆求与内切圆相关的问题。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 什么是圆的切线长?切线长定理是什么? 切线上一点到切点之间的线段长叫做这点到圆的切线长;过圆外一点作圆的两条切线,两条切线长相等,圆心与这一点的连线平分两条切线的夹角。 学生回答问题,其他学生进行补充回答,以培养学生温顾知新的好习惯. 由上节切线长定理,导入本节课,进行知识的迁移。
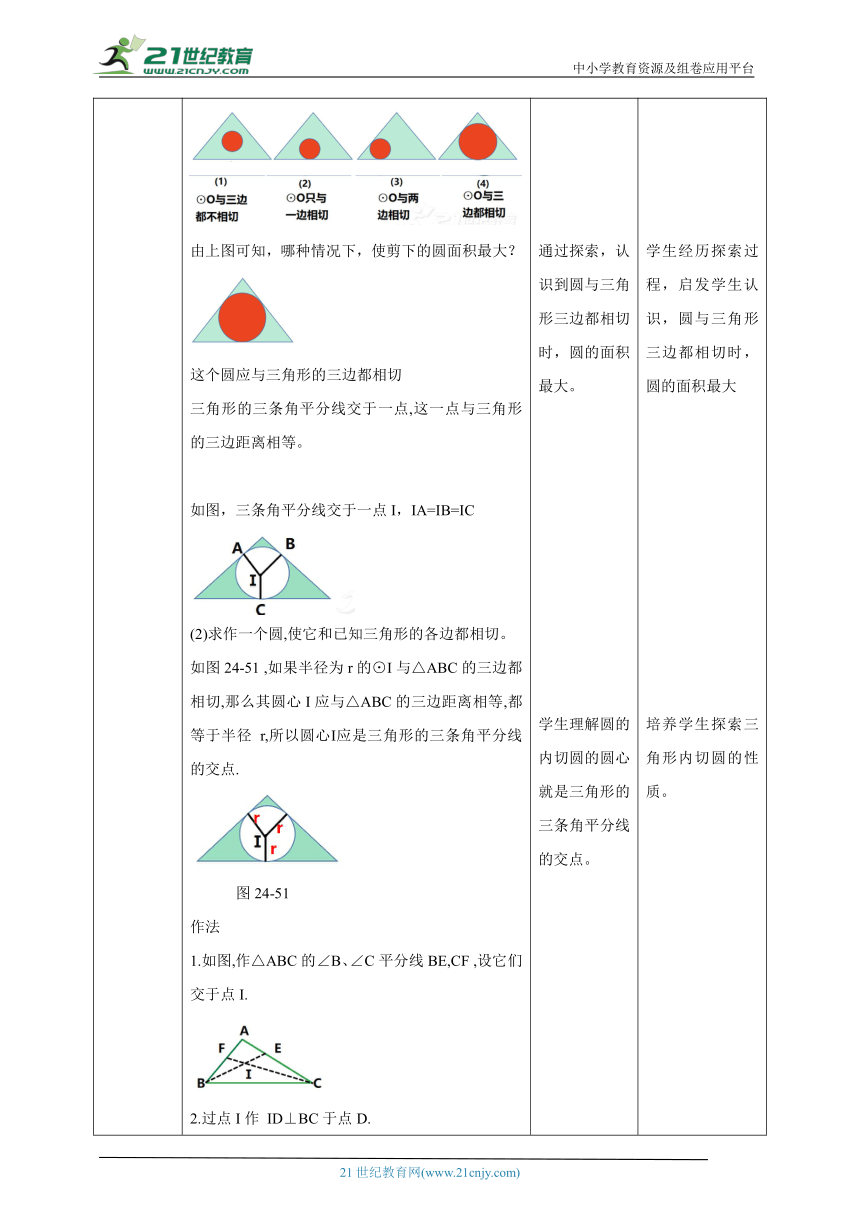
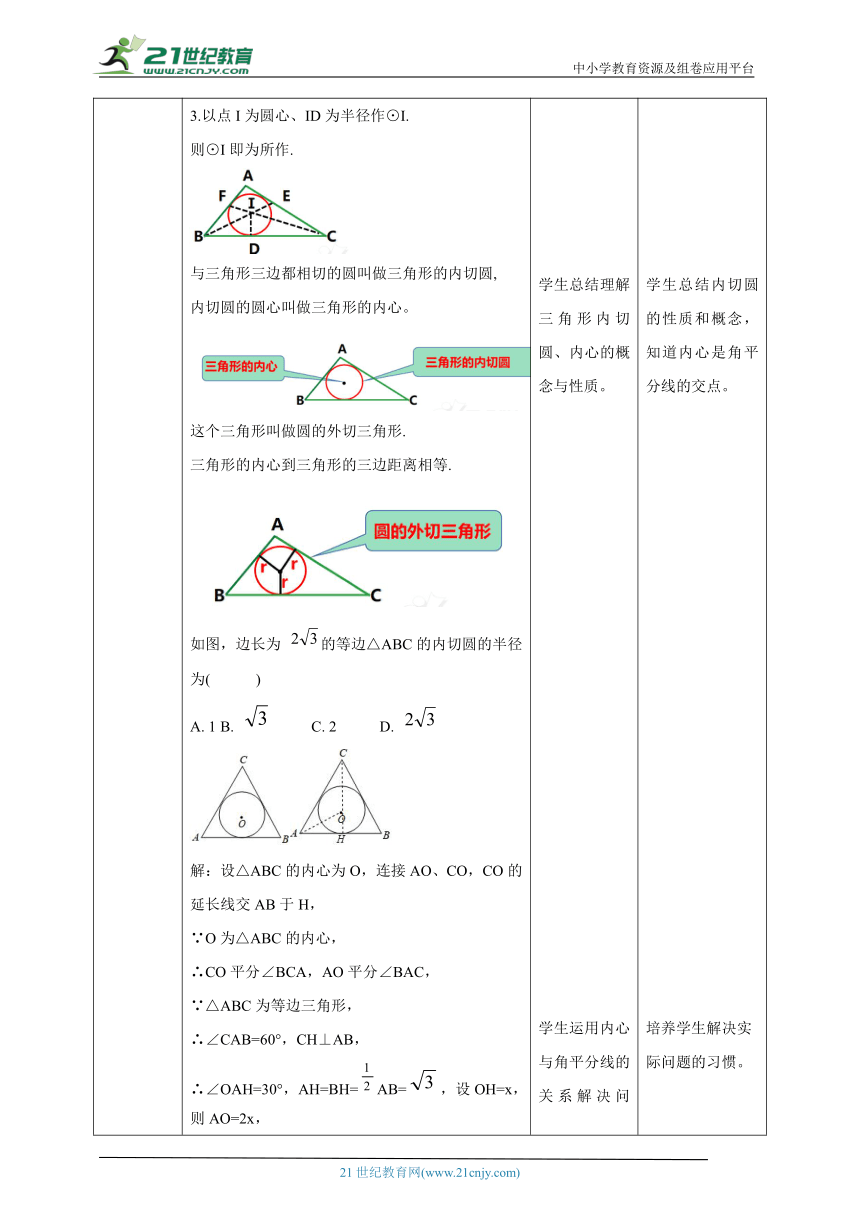
讲授新课 探究有一块三角形材料,如何从中剪下一个面积最大的圆 (1)如果最大圆存在,它与三角形的各边应有怎样的位置关系 2.如图24-50,⊙O按其位置与三角形的边是否相切分四种情形:由上图可知,哪种情况下,使剪下的圆面积最大?这个圆应与三角形的三边都相切三角形的三条角平分线交于一点,这一点与三角形的三边距离相等。 如图,三条角平分线交于一点I,IA=IB=IC(2)求作一个圆,使它和已知三角形的各边都相切。如图24-51 ,如果半径为r的⊙I与△ABC的三边都相切,那么其圆心I应与△ABC的三边距离相等,都等于半径 r,所以圆心Ⅰ应是三角形的三条角平分线的交点.图24-51作法1.如图,作△ABC的∠B、∠C平分线BE,CF ,设它们交于点I.2.过点I作 ID⊥BC于点D.3.以点I为圆心、ID为半径作⊙I.则⊙I即为所作.与三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心。这个三角形叫做圆的外切三角形.三角形的内心到三角形的三边距离相等.如图,边长为 的等边△ABC的内切圆的半径为( )A. 1 B. C. 2 D. 解:设△ABC的内心为O,连接AO、CO,CO的延长线交AB于H,∵O为△ABC的内心,∴CO平分∠BCA,AO平分∠BAC,∵△ABC为等边三角形,∴∠CAB=60°,CH⊥AB,∴∠OAH=30°,AH=BH=AB=,设OH=x,则AO=2x,在Rt△AOH中,由勾股定理得: ∴x=1,∴OH=1,即△ABC内切圆的半径为1.故选:A. 例 如图 ,在△ABC中,∠B=43°,∠C =61°,点I是△ABC的内心,求∠BIC的度数.分析:根据内心是角平分线的交点,在△BIC中,求出∠IBC+∠ICB与∠B+∠C的关系,即可求出∠BIC的度数。解:连接IB,IC.因为点I是△ABC的内心,所以 IB,IC分别是∠B、∠C的平分线在△IBC中,有∠BIC = 180°-(∠IBC+∠ICB)=180°- (∠B +∠C)=180°-(43°+61°)=128°. 学生独立思考问题,发表自己的见解,大胆提出如何求三角形中面积最大的圆,学会倾听别的同学的意见。通过探索,认识到圆与三角形三边都相切时,圆的面积最大。学生理解圆的内切圆的圆心就是三角形的三条角平分线的交点。 学生总结理解三角形内切圆、内心的概念与性质。学生运用内心与角平分线的关系解决问题。 通过锻炼学生观察能力,让学生认识内切圆的概念。学生经历探索过程,启发学生认识,圆与三角形三边都相切时,圆的面积最大培养学生探索三角形内切圆的性质。 学生总结内切圆的性质和概念,知道内心是角平分线的交点。培养学生解决实际问题的习惯。
课堂练习 1.如图所示的网格由边长为1个单位长度的小正方形组成,点A、B、C在直角坐标系中的坐标分别为(3,6),(-3,3),(7,-2),则△ABC内心的坐标为______.解:如图,点I即为△ABC的内心.I为三角形三个内角平分线的交点,如图易得点I的纵坐标为3,∠ACB的平分线经过(5,0)和(4,1)所以该角平分线所在的直线为:y=-x+5,当y=3时,解得x=2所以△ABC内心I的坐标为(2,3).故答案为:(2,3).2.如图,在Rt ABC中,∠C=90°,AC=5,⊙O是 ABC的内切圆,半径为2,则图中阴影部分的面积为 ( )A. 30-4π B. C. 60-16π D. 30-16π解:如图,记三个切点分别为D、E、F,连接OD、OE、OF,则∠ODC=∠OEC=∠OFA=90°,OD=OE=OF=2,∴四边形ODCE是正方形,∴CE=CD=2,∵⊙O是 ABC的内切圆,∴AE=AF=5-2=3,BD=BF,设BD=BF=x,则BC=x+2,AB=x+3,在Rt ABC中,AC2+BC2=AB2,即52+(x+2)2=(x+3)2,∴x=10,∴BC=12,∴S阴影部分=S ABC-S⊙O =×5×12-π×22=30-4π.故选A.如图,⊙O为△ABC的内切圆,切点为E,F,G.∠C=90°,AO的延长线交BC于点D,AC=4,CD=1.求⊙O的半径r.解:连结OE、OF,如图,∵⊙O为△ABC的内切圆,∴OE⊥BC,OF⊥AC,而∠C=90°,∴四边形OECF为正方形,∴OE=CE=r,∵OE//AC,∴△DOE∽△DAC,∴ ,即,∴ . 学生做本节内切圆的性质,互相补充,教师订正答案,做最后总结切线长定理。 练习是为了巩固学生所学的新知,教会学生利用内切圆的性质解决问题,同时培养学生的推理能力。
课堂小结 学生先发言总结本节内切圆的性质,在教师的引导下总结归纳。 让学生自己对本节课知识进行整合归纳,培养学生养成一种对所学知识进行总结的良好习惯,形成知识体系.
板书 课题:24.5 三角形的内切圆1.作出内切圆2.内切圆概念3.例题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
沪科版九年级下册数学24.5三角形的内切圆 教学设计
课题 24.5三角形的内切圆 单元 第24单元 学科 数学 年级 九
教材分析 前面学习了圆的切线的性质和判定,本节在此基础上,研究了三角形内切圆的问题,首先理解三角形的内切圆、三角形的内心等概念;还学习了作出一个三角形的内切圆,并利用内心的概念来求角、边等综合问题。
核心素养分析 本节重点研究了三角形的内切圆,学会作出一个三角形的内切圆,锻炼了学生的动手操作能力,还有利用内切圆求角、边等综合问题,培养了学生的计算能力和推理能力。
学习目标 1.理解三角形的内切圆概念;2.作出三角形的内切圆,理解三角形的内切圆的步骤;3.能根据三角形的内切圆求与内切圆相关的问题。
重点 作出三角形的内切圆,理解三角形的内切圆的步骤。
难点 能根据三角形的内切圆求与内切圆相关的问题。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 什么是圆的切线长?切线长定理是什么? 切线上一点到切点之间的线段长叫做这点到圆的切线长;过圆外一点作圆的两条切线,两条切线长相等,圆心与这一点的连线平分两条切线的夹角。 学生回答问题,其他学生进行补充回答,以培养学生温顾知新的好习惯. 由上节切线长定理,导入本节课,进行知识的迁移。
讲授新课 探究有一块三角形材料,如何从中剪下一个面积最大的圆 (1)如果最大圆存在,它与三角形的各边应有怎样的位置关系 2.如图24-50,⊙O按其位置与三角形的边是否相切分四种情形:由上图可知,哪种情况下,使剪下的圆面积最大?这个圆应与三角形的三边都相切三角形的三条角平分线交于一点,这一点与三角形的三边距离相等。 如图,三条角平分线交于一点I,IA=IB=IC(2)求作一个圆,使它和已知三角形的各边都相切。如图24-51 ,如果半径为r的⊙I与△ABC的三边都相切,那么其圆心I应与△ABC的三边距离相等,都等于半径 r,所以圆心Ⅰ应是三角形的三条角平分线的交点.图24-51作法1.如图,作△ABC的∠B、∠C平分线BE,CF ,设它们交于点I.2.过点I作 ID⊥BC于点D.3.以点I为圆心、ID为半径作⊙I.则⊙I即为所作.与三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心。这个三角形叫做圆的外切三角形.三角形的内心到三角形的三边距离相等.如图,边长为 的等边△ABC的内切圆的半径为( )A. 1 B. C. 2 D. 解:设△ABC的内心为O,连接AO、CO,CO的延长线交AB于H,∵O为△ABC的内心,∴CO平分∠BCA,AO平分∠BAC,∵△ABC为等边三角形,∴∠CAB=60°,CH⊥AB,∴∠OAH=30°,AH=BH=AB=,设OH=x,则AO=2x,在Rt△AOH中,由勾股定理得: ∴x=1,∴OH=1,即△ABC内切圆的半径为1.故选:A. 例 如图 ,在△ABC中,∠B=43°,∠C =61°,点I是△ABC的内心,求∠BIC的度数.分析:根据内心是角平分线的交点,在△BIC中,求出∠IBC+∠ICB与∠B+∠C的关系,即可求出∠BIC的度数。解:连接IB,IC.因为点I是△ABC的内心,所以 IB,IC分别是∠B、∠C的平分线在△IBC中,有∠BIC = 180°-(∠IBC+∠ICB)=180°- (∠B +∠C)=180°-(43°+61°)=128°. 学生独立思考问题,发表自己的见解,大胆提出如何求三角形中面积最大的圆,学会倾听别的同学的意见。通过探索,认识到圆与三角形三边都相切时,圆的面积最大。学生理解圆的内切圆的圆心就是三角形的三条角平分线的交点。 学生总结理解三角形内切圆、内心的概念与性质。学生运用内心与角平分线的关系解决问题。 通过锻炼学生观察能力,让学生认识内切圆的概念。学生经历探索过程,启发学生认识,圆与三角形三边都相切时,圆的面积最大培养学生探索三角形内切圆的性质。 学生总结内切圆的性质和概念,知道内心是角平分线的交点。培养学生解决实际问题的习惯。
课堂练习 1.如图所示的网格由边长为1个单位长度的小正方形组成,点A、B、C在直角坐标系中的坐标分别为(3,6),(-3,3),(7,-2),则△ABC内心的坐标为______.解:如图,点I即为△ABC的内心.I为三角形三个内角平分线的交点,如图易得点I的纵坐标为3,∠ACB的平分线经过(5,0)和(4,1)所以该角平分线所在的直线为:y=-x+5,当y=3时,解得x=2所以△ABC内心I的坐标为(2,3).故答案为:(2,3).2.如图,在Rt ABC中,∠C=90°,AC=5,⊙O是 ABC的内切圆,半径为2,则图中阴影部分的面积为 ( )A. 30-4π B. C. 60-16π D. 30-16π解:如图,记三个切点分别为D、E、F,连接OD、OE、OF,则∠ODC=∠OEC=∠OFA=90°,OD=OE=OF=2,∴四边形ODCE是正方形,∴CE=CD=2,∵⊙O是 ABC的内切圆,∴AE=AF=5-2=3,BD=BF,设BD=BF=x,则BC=x+2,AB=x+3,在Rt ABC中,AC2+BC2=AB2,即52+(x+2)2=(x+3)2,∴x=10,∴BC=12,∴S阴影部分=S ABC-S⊙O =×5×12-π×22=30-4π.故选A.如图,⊙O为△ABC的内切圆,切点为E,F,G.∠C=90°,AO的延长线交BC于点D,AC=4,CD=1.求⊙O的半径r.解:连结OE、OF,如图,∵⊙O为△ABC的内切圆,∴OE⊥BC,OF⊥AC,而∠C=90°,∴四边形OECF为正方形,∴OE=CE=r,∵OE//AC,∴△DOE∽△DAC,∴ ,即,∴ . 学生做本节内切圆的性质,互相补充,教师订正答案,做最后总结切线长定理。 练习是为了巩固学生所学的新知,教会学生利用内切圆的性质解决问题,同时培养学生的推理能力。
课堂小结 学生先发言总结本节内切圆的性质,在教师的引导下总结归纳。 让学生自己对本节课知识进行整合归纳,培养学生养成一种对所学知识进行总结的良好习惯,形成知识体系.
板书 课题:24.5 三角形的内切圆1.作出内切圆2.内切圆概念3.例题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
