【新课标】2.3 垂径定理 课件(共34张PPT)
文档属性
| 名称 | 【新课标】2.3 垂径定理 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 09:33:11 | ||
图片预览










文档简介
(共34张PPT)
2.3 垂径定理
湘教版 九年级下
教学内容分析
学完前面3节,重点学习了圆的概念,圆周角圆心角的概念,圆周角定理及其推论,本节课重点学习一下,垂直于弦的直径的性质。
教学目标
1.证明和理解垂径定理(重点)
2.运用垂径定理,解决圆与三角形、四边形综合知识解答问题(难点)
核心素养分析
本节内容主要研究垂径定理,定理的条件是垂直于弦的直径,结论有直径平分这条弦,直径平分这条弦所对的两条弧。在证明的过程中,培养了学生几何直观的观念,也提高了学生的计算能力。
新知导入
直径所对的圆周角是_______;
90°的圆周角所对的弦是_______.
圆内接四边形的对角_______.
直角
直径
互补
新知讲解
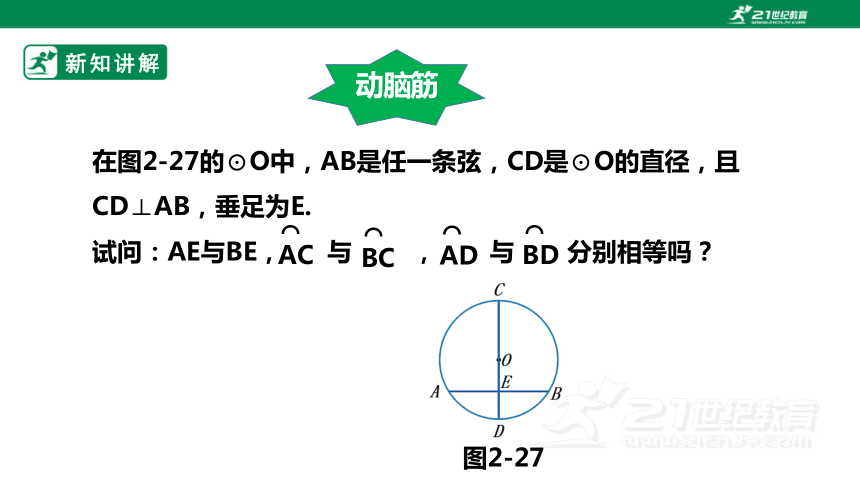
在图2-27的⊙O中,AB是任一条弦,CD是⊙O的直径,且CD⊥AB,垂足为E.
试问:AE与BE, 与 , 与 分别相等吗?
动脑筋
⌒
BC
⌒
AC
⌒
AD
⌒
BD
图2-27
新知讲解
因为圆是轴对称图形,将⊙O沿直径CD对折,如图2-28,我们发现AE与BE重合, , 分别与 , 重合,即AE=BE, = , = .
⌒
AC
⌒
AD
⌒
BC
⌒
BD
⌒
AC
⌒
BC
⌒
AD
⌒
BD
图2-28
D
C
O
E
B(A)
解:连接OA,OB.
∵ OA=OB,
∴ △OAB是等腰三角形.
∵OE⊥AB,
∴AE=BE,∠AOD=∠BOD.
从而∠AOC=∠BOC.
∴ = , = .
新知讲解
⌒
AC
⌒
BC
⌒
AD
⌒
BD
------
------
以两条半径及所夹的弦构成的等腰三角形
新知讲解
由此得到垂径定理:
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
------
------
∵ CD是直径,CD⊥AB,
∴ AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
新知讲解
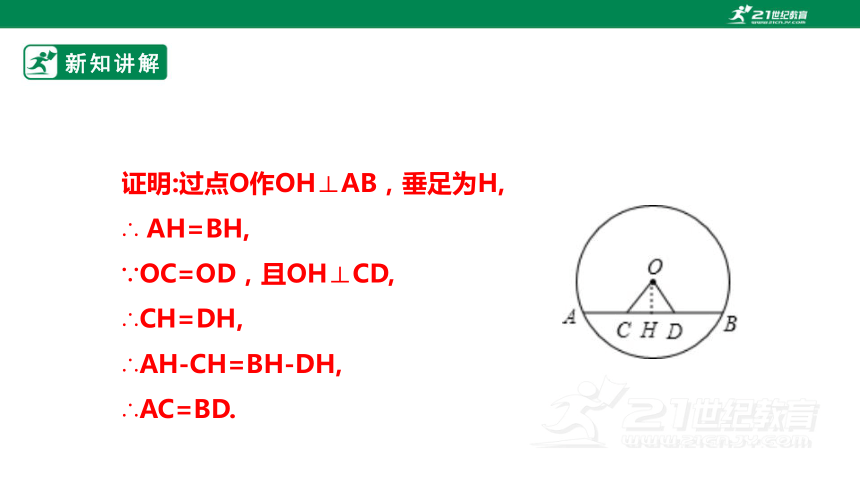
变式1 如图,AB是⊙O的弦,点C、D在弦AB上,且OC= OD. 求证:AC= BD.
新知讲解
证明:过点O作OH⊥AB,垂足为H,
∴ AH=BH,
∵OC=OD,且OH⊥CD,
∴CH=DH,
∴AH-CH=BH-DH,
∴AC=BD.
新知讲解
例1 如图2-29,弦AB=8cm,CD是⊙O的直径,CD⊥AB,垂足为E,DE=2cm,求⊙O的直径CD的长.
图2-29
新知讲解
解 连接OA.
设OA=rcm, 则OE=r-2(cm).
∵CD⊥AB,
由垂径定理得 AE=AB÷2=4(cm).
在Rt△AEO中,
由勾股定理得OA2= OE2+AE2.
即r2=(r-2)2+42.
解得r=5 .
∴CD=2r=10(cm)
图2-29
------
过圆心作弦的垂线构成直角三角形
新知讲解
例2 证明: 圆的两条平行弦所夹的弧相等.
根据命题画图;
写出已知求证;
写出证明过程.
新知讲解
已知:如图2-30, 在⊙O中,弦AB与弦CD平行.
求证: = .
⌒
AC
⌒
BD
图2-30
新知讲解
证明 作直径EF⊥AB,
∴ = .
又 ∵ AB//CD,EF⊥AB,
∴EF⊥CD.
∴ = .
因此 ,
即 .
⌒
CE
⌒
DE
⌒ ⌒ ⌒ ⌒
AE- CE= BE-DE
⌒ ⌒
AC=BD
-------------
E
F
⌒
AE
⌒
BE
新知讲解
变式2:如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,OC =3,则EC的长为( )
A.6 B.8 C.7 D.
解:连接BE,
∵AE为⊙O直径,
∴∠ABE =90°,
∵OD⊥AB,OD过点O,
∴AC=BC= AB=2×8=4
新知讲解
连接直径所对的弧上的点与直径端点,构成直角三角形
新知讲解
∵AO = OE,
∴BE =2OC,
∵OC = 3,
∴BE= 6,
在Rt △ CBE中,
故选:D.
根据以上题目,在圆中添加辅助线构成的三角形的常用方法:
新知讲解
------
------
连接AO,OB,构成等腰三角形AOB
------
连接AO,构成直角三角形AOE
连接EB,构成直角三角形AEB
1.如图,DC是⊙O的直径,弦AB⊥CD于点F,则下列结论不一定正确的是 ( )
A. B. AF=BF C. OF=CF D.
课堂练习
C
⌒ ⌒
AD= BD
⌒ ⌒
AC= BC
课堂练习
解:∵DC是⊙O的直径,弦AB⊥CD,
∴点D是优弧AB的中点,点C是劣弧AB的中点,
且AF=BF,
故选项A,B,D一定正确;
无法证明OF=CF,
故选C.
课堂练习
2.如图,在⊙O内有折线OABC,其中OA =8,AB=12,∠A =∠B =60°,则BC的长为( )
A.16 B.20 C.18 D.22
课堂练习
解:延长AO交BC于D,作OE⊥BC于E.
∵∠A=∠B=60,
∴ADB =60°;
∴△ADB为等边三角形;
∴BD=AD =AB =12;
∴OD = 4,
课堂练习
∴OD= 4,
又∵∠ADB =60°,
∴DE= OD = 2;
∴BE=10;
∴BC=2BE = 20;
故选:B.
课堂练习
3.已知⊙O的半径为10,弦AB//CD,AB=12,CD=16,则AB和CD的距离为______________.
14或2
课堂练习
分两种情况:
①当AB、CD在圆心O的两侧时,如图1,
过O作OE⊥CD于E,延长EO交AB于F,连接OD、OB,
∵AB//CD,
∴EF⊥AB,
∴ED= CD,BF= AB,
课堂练习
∵AB=12,CD=16,
∴ED=8,BF=6,
由勾股定理得:
OE2=OD2-ED2 =102-82 =62,
OF2=OB2-BF2 =102-62=82,
∴EF=OE+OF=6+8=14
课堂练习
②当AB、CD在圆心O的同侧时,如图2,
同理得:
EF=OF-OE=8-6=2,
综上所述,AB和CD的距离为14或2.
课堂总结
1、什么是垂径定理?
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
2、怎样在圆中添加辅助线构成的三角形?
连接AO,OB,构成等腰三角形AOB
连接AO,构成直角三角形AOE
连接EB,构成直角三角形AEB
板书设计
2.3 垂径定理
1.垂径定理
2.例1
例2
作业布置
必做题:课本60页的练习第1,2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.3 垂径定理
湘教版 九年级下
教学内容分析
学完前面3节,重点学习了圆的概念,圆周角圆心角的概念,圆周角定理及其推论,本节课重点学习一下,垂直于弦的直径的性质。
教学目标
1.证明和理解垂径定理(重点)
2.运用垂径定理,解决圆与三角形、四边形综合知识解答问题(难点)
核心素养分析
本节内容主要研究垂径定理,定理的条件是垂直于弦的直径,结论有直径平分这条弦,直径平分这条弦所对的两条弧。在证明的过程中,培养了学生几何直观的观念,也提高了学生的计算能力。
新知导入
直径所对的圆周角是_______;
90°的圆周角所对的弦是_______.
圆内接四边形的对角_______.
直角
直径
互补
新知讲解
在图2-27的⊙O中,AB是任一条弦,CD是⊙O的直径,且CD⊥AB,垂足为E.
试问:AE与BE, 与 , 与 分别相等吗?
动脑筋
⌒
BC
⌒
AC
⌒
AD
⌒
BD
图2-27
新知讲解
因为圆是轴对称图形,将⊙O沿直径CD对折,如图2-28,我们发现AE与BE重合, , 分别与 , 重合,即AE=BE, = , = .
⌒
AC
⌒
AD
⌒
BC
⌒
BD
⌒
AC
⌒
BC
⌒
AD
⌒
BD
图2-28
D
C
O
E
B(A)
解:连接OA,OB.
∵ OA=OB,
∴ △OAB是等腰三角形.
∵OE⊥AB,
∴AE=BE,∠AOD=∠BOD.
从而∠AOC=∠BOC.
∴ = , = .
新知讲解
⌒
AC
⌒
BC
⌒
AD
⌒
BD
------
------
以两条半径及所夹的弦构成的等腰三角形
新知讲解
由此得到垂径定理:
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
------
------
∵ CD是直径,CD⊥AB,
∴ AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
新知讲解
变式1 如图,AB是⊙O的弦,点C、D在弦AB上,且OC= OD. 求证:AC= BD.
新知讲解
证明:过点O作OH⊥AB,垂足为H,
∴ AH=BH,
∵OC=OD,且OH⊥CD,
∴CH=DH,
∴AH-CH=BH-DH,
∴AC=BD.
新知讲解
例1 如图2-29,弦AB=8cm,CD是⊙O的直径,CD⊥AB,垂足为E,DE=2cm,求⊙O的直径CD的长.
图2-29
新知讲解
解 连接OA.
设OA=rcm, 则OE=r-2(cm).
∵CD⊥AB,
由垂径定理得 AE=AB÷2=4(cm).
在Rt△AEO中,
由勾股定理得OA2= OE2+AE2.
即r2=(r-2)2+42.
解得r=5 .
∴CD=2r=10(cm)
图2-29
------
过圆心作弦的垂线构成直角三角形
新知讲解
例2 证明: 圆的两条平行弦所夹的弧相等.
根据命题画图;
写出已知求证;
写出证明过程.
新知讲解
已知:如图2-30, 在⊙O中,弦AB与弦CD平行.
求证: = .
⌒
AC
⌒
BD
图2-30
新知讲解
证明 作直径EF⊥AB,
∴ = .
又 ∵ AB//CD,EF⊥AB,
∴EF⊥CD.
∴ = .
因此 ,
即 .
⌒
CE
⌒
DE
⌒ ⌒ ⌒ ⌒
AE- CE= BE-DE
⌒ ⌒
AC=BD
-------------
E
F
⌒
AE
⌒
BE
新知讲解
变式2:如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,OC =3,则EC的长为( )
A.6 B.8 C.7 D.
解:连接BE,
∵AE为⊙O直径,
∴∠ABE =90°,
∵OD⊥AB,OD过点O,
∴AC=BC= AB=2×8=4
新知讲解
连接直径所对的弧上的点与直径端点,构成直角三角形
新知讲解
∵AO = OE,
∴BE =2OC,
∵OC = 3,
∴BE= 6,
在Rt △ CBE中,
故选:D.
根据以上题目,在圆中添加辅助线构成的三角形的常用方法:
新知讲解
------
------
连接AO,OB,构成等腰三角形AOB
------
连接AO,构成直角三角形AOE
连接EB,构成直角三角形AEB
1.如图,DC是⊙O的直径,弦AB⊥CD于点F,则下列结论不一定正确的是 ( )
A. B. AF=BF C. OF=CF D.
课堂练习
C
⌒ ⌒
AD= BD
⌒ ⌒
AC= BC
课堂练习
解:∵DC是⊙O的直径,弦AB⊥CD,
∴点D是优弧AB的中点,点C是劣弧AB的中点,
且AF=BF,
故选项A,B,D一定正确;
无法证明OF=CF,
故选C.
课堂练习
2.如图,在⊙O内有折线OABC,其中OA =8,AB=12,∠A =∠B =60°,则BC的长为( )
A.16 B.20 C.18 D.22
课堂练习
解:延长AO交BC于D,作OE⊥BC于E.
∵∠A=∠B=60,
∴ADB =60°;
∴△ADB为等边三角形;
∴BD=AD =AB =12;
∴OD = 4,
课堂练习
∴OD= 4,
又∵∠ADB =60°,
∴DE= OD = 2;
∴BE=10;
∴BC=2BE = 20;
故选:B.
课堂练习
3.已知⊙O的半径为10,弦AB//CD,AB=12,CD=16,则AB和CD的距离为______________.
14或2
课堂练习
分两种情况:
①当AB、CD在圆心O的两侧时,如图1,
过O作OE⊥CD于E,延长EO交AB于F,连接OD、OB,
∵AB//CD,
∴EF⊥AB,
∴ED= CD,BF= AB,
课堂练习
∵AB=12,CD=16,
∴ED=8,BF=6,
由勾股定理得:
OE2=OD2-ED2 =102-82 =62,
OF2=OB2-BF2 =102-62=82,
∴EF=OE+OF=6+8=14
课堂练习
②当AB、CD在圆心O的同侧时,如图2,
同理得:
EF=OF-OE=8-6=2,
综上所述,AB和CD的距离为14或2.
课堂总结
1、什么是垂径定理?
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
2、怎样在圆中添加辅助线构成的三角形?
连接AO,OB,构成等腰三角形AOB
连接AO,构成直角三角形AOE
连接EB,构成直角三角形AEB
板书设计
2.3 垂径定理
1.垂径定理
2.例1
例2
作业布置
必做题:课本60页的练习第1,2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
