高中数学北师大(2019)必修第二册限时训练——1.3弧度制2(含解析)
文档属性
| 名称 | 高中数学北师大(2019)必修第二册限时训练——1.3弧度制2(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 947.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-07 00:00:00 | ||
图片预览




文档简介
一、单选题
1.已知一扇形的周长为,则当该扇形的面积取得最大时,圆心角大小为( )
A. B. C.1 D.2
2.若扇形的周长为定值,圆心角为,则当扇形的面积取得最大值时,该扇形的圆心角的值为( )
A.1 B.2 C.3 D.4
3.已知平面上的线段l及点P,任取l上的一点Q,线段PQ长度的最小值称为点P到线段l的距离,记作,若曲线C是边长为4的等边三角形,则点集所表示的图形面积为( )
A. B.
C. D.
4.中国折叠扇有着深厚的文化底蕴.如图(2),在半圆中作出两个扇形和,用扇环形(图中阴影部分)制作折叠扇的扇面.记扇环形的面积为,扇形的面积为,当与的比值为时,扇面的形状较为美观,则此时扇形的半径与半圆的半径之比为
A. B. C. D.
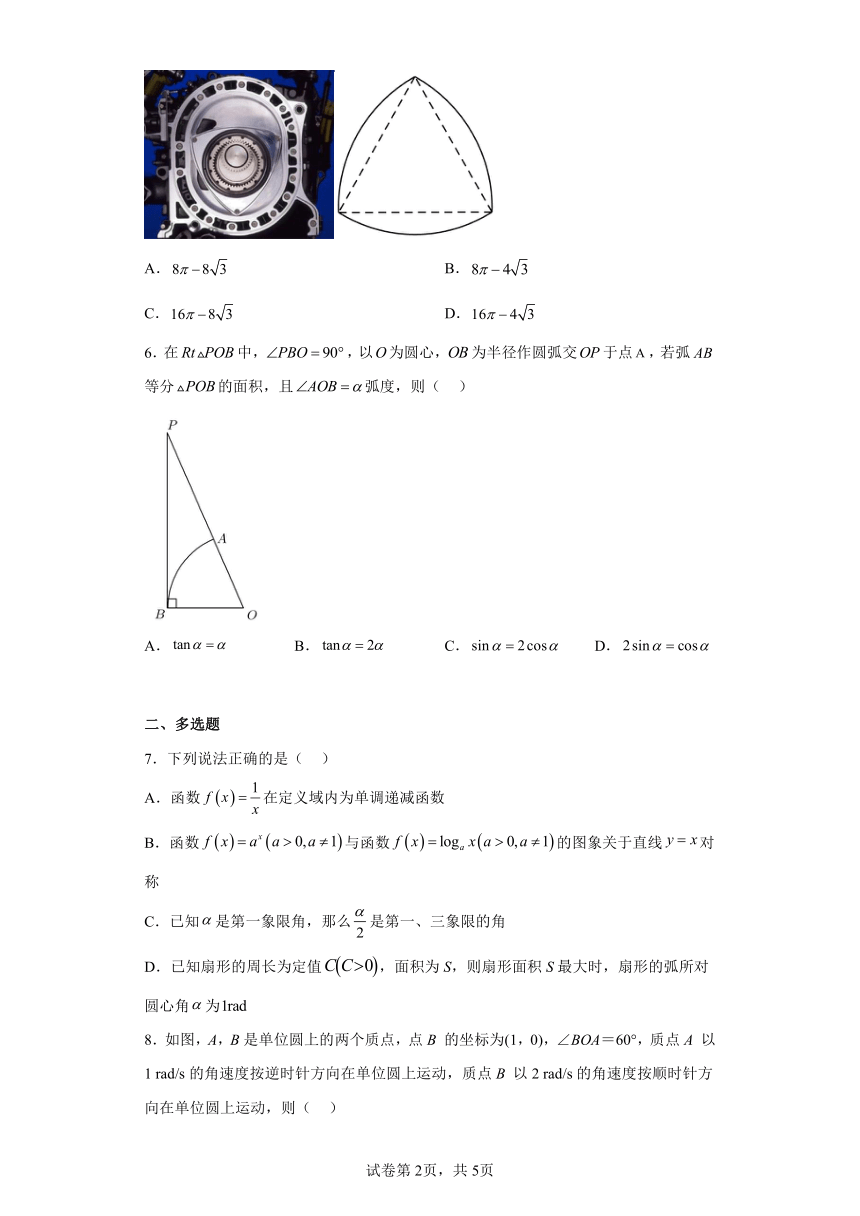
5.“莱洛三角形”是机械学家莱洛研究发现的一种曲边三角形,转子发动机的设计就是利用了莱洛三角形,转子引擎只需转一周,各转子便有一次进气、压缩、点火与排气过程,相当于往复式引擎运转两周,因此具有小排气量就能成就高动力输出的优点.另外,由于转子引擎的轴向运动特性,它不需要精密的曲轴平衡就可以达到非常高的运转转速.“莱洛三角形”是分别以正三角形的顶点为圆心,以其边长为半径作圆弧,由这三段圆弧组成的曲边三角形(如图所示).设“莱洛三角形”曲边上两点之间的最大距离为4,则该“莱洛三角形”的面积为( )
A. B.
C. D.
6.在中,,以为圆心,为半径作圆弧交于点,若弧等分的面积,且弧度,则( )
A. B. C. D.
二、多选题
7.下列说法正确的是( )
A.函数在定义域内为单调递减函数
B.函数与函数的图象关于直线对称
C.已知是第一象限角,那么是第一、三象限的角
D.已知扇形的周长为定值,面积为S,则扇形面积S最大时,扇形的弧所对圆心角为
8.如图,A,B是单位圆上的两个质点,点B 的坐标为(1,0),∠BOA=60°,质点A 以1 rad/s的角速度按逆时针方向在单位圆上运动,质点B 以2 rad/s的角速度按顺时针方向在单位圆上运动,则( )
A.经过1 s后,∠BOA的弧度数为+3
B.经过 s后,扇形AOB的弧长为
C.经过s后,扇形AOB的面积为
D.经过 s后,A,B在单位圆上第一次相遇
三、填空题
9.某设计师为天文馆设计科普宣传图片,其中有一款设计图如图所示.是一个以点O为圆心 长为直径的半圆,.的圆心为P,.与所围的灰色区域即为某天所见的月亮形状,则该月亮形状的面积为___________.
10.我国古代数学著作《九章算术》中《方田》章有弧田面积计算问题,计算术曰:以弦乘矢,矢又自乘,并之,二而一其大意是,弧田面积计算公式为:弧田面积(弦×矢+矢).如图所示的弧田由圆弧和其所对弦围成,公式中“弦”指圆弧所对弦长,“矢”指圆弧顶到弦的距离(等于半径长与圆心到弦的距离之差),现有一圆弧所对圆心角为,弧长为的弧田,按照上述经验公式计算所得弧田面积是______.
11.已知扇形的周长为8cm,则该扇形面积的最大值为________cm2.
12.已知扇形的圆心角为,弧长为,则其面积为___________.
四、解答题
13.已知一个扇形的周长为,求当扇形的圆心角多大时,扇形的面积最大,并求这个最大值.
14.某地政府部门欲做一个“践行核心价值观”的宣传牌,该宣传牌形状是如图所示的扇形环面(由扇形挖去扇形后构成的).已知米,米,线段、线段与弧、弧的长度之和为米,圆心角为弧度.
(1)求关于的函数解析式;
(2)记该宣传牌的面积为,试问取何值时,的值最大 并求出最大值.
15.如图,用弧度表示顶点在原点,始边重合于x轴的非负半轴,终边落在阴影部分内的角的集合(不包括边界).
(1) ;
(2)
16.已知相互咬合的两个齿轮,大轮有48齿,小轮有20齿,当大轮顺时针转动一周时,小轮转动的角是多少度?多少弧度?如果大轮的转速是150r/min,小轮的半径为10cm,那么小轮圆周上的点每秒转过的弧长是多少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据周长建立弧长与半径间的关系,由扇形面积公式可得,利用二次函数求最值,并求出S最大时对应的圆心角即可.
【详解】设扇形的半径为,弧长为,则,
所以,
扇形面积,
当时,有最大值,此时圆心角,
故选:D
2.B
【分析】根据扇形的弧长公式和面积公式,将面积写成关于的表达式,再利用二次函数性质即可求得结果.
【详解】设扇形的半径为,弧长为,
因此,
扇形的面积,
由二次函数性质可知,当时,扇形面积取到最大值;
此时,.
故选:B
3.B
【分析】根据条件可画出满足题意的点集所表示的图形,分别求解区域各个构成部分的面积,进而即得.
【详解】由题意,点集D所表示的图形如图,是边长为4的正三角形,
其中,,,,,
,,
所以扇形的面积为,
,,
,
所以的面积为,
又,
所以四边形的面积为,
又四边形的面积为,
点集所表示的图形面积为:
.
故选:B.
4.B
【解析】扇环形的面积等于扇形的面积减扇形的面积;设半径代入求解.
【详解】设,半圆的半径为,扇形的半径为,
依题意,有,即,
所以,得.
故选:B.
【点睛】本题考查弧度制下扇形面积计算问题.
其解题策思路:
(1)明确弧度制下扇形面积公式,在使用公式时,要注意角的单位必须是弧度.
(2)分析题目已知哪些量、要求哪些量,然后灵活地运用弧长公式、扇形面积公式直接求解,或合理地利用圆心角所在三角形列方程(组)求解.
5.A
【分析】先根据图形特征求得,从而,再求出扇形ABC的面积,最后根据“莱洛三角形”面积与扇形面积之间的关系求出其面积即可.
【详解】解:由题意可知等边三角形的边长为4,即,
所以扇形ABC的面积等于以A为圆心,为半径的圆的面积的,
故扇形ABC的面积,
又,
该“莱洛三角形”的面积为.
故选:A.
6.B
【分析】分析题意,首先设出扇形的半径,表示出扇形的面积和直角三角形的面积,列方程即可求得.
【详解】设扇形的半径为r,则扇形的面积为.
直角三角形POB中,,△POB的面积为.
由题意得,所以.
故选:B
7.BC
【分析】根据单调性判断A选项;根据指数函数与对数函数互为反函数判断B选项;根据角的范围判断C选项;根据扇形面积公式与周长结合二次函数性质求解判断D选项.
【详解】解:对于A选项,函数定义域为,在和上单调递减,在定义域上无单调性,故错误;
对于B选项,指数函数与对数函数互为反函数,图像关于直线对称,故正确;
对于C选项,若是第一象限角,则,故,所以当为偶数时,为第一象限角,为奇数时,为第三象限角,故正确;
对于D选项,由已知,故,所以,故当时,面积最大,此时圆心角,故错误;
故选:BC
8.ABD
【分析】结合条件根据扇形面积,弧长公式逐项分析即得.
【详解】经过1 s后,质点A运动1 rad,质点B运动2 rad,此时∠BOA的弧度数为,故A正确;
经过 s后,,故扇形AOB的弧长为,故B正确;
经过 s后,,故扇形AOB的面积为,故C不正确;
设经过t s后,A,B在单位圆上第一次相遇,则,解得 (s),故D正确.
故选:ABD.
9.
【分析】连接,可得,求出,利用割补法即可求出月牙的面积.
【详解】解:连接,可得,
因为,
所以,,
所以月牙的面积为.
故答案为:.
10.
【分析】由条件根据弧长公式求半径,解直角三角形可得弦、矢的值,求出弧田面积.
【详解】如图:
由题意可得,弧的长为,
所以,故,
在中,可得,,,可得矢,
由,可得弦,
所以弧田面积(弦矢矢.
故答案为:.
11.4
【分析】扇形的周长为, ,,转化为同种变量,利用二次函数最值即可求解.
【详解】设扇形半径为cm,弧长为 cm,则,,所以当时, (cm2).
故答案为:4.
12.
【分析】根据扇形的弧长公式求出半径,再计算扇形的面积.
【详解】扇形的圆心角为,弧长为,
则扇形的半径为r,
面积为.
故答案为:.
13.当扇形的圆心角为时,扇形的面积最大,最大值为.
【分析】设扇形的弧长为,半径为,圆心角为,面积为,可得,由,,可得的范围,根据二次函数的性质求得面积的最大值,再由可得面积取得最大值时的圆心角.
【详解】设扇形的弧长为,半径为,圆心角为,面积为.
由已知,可得,
所以扇形的面积,
因为,,所以,
所以当时,,此时, 所以,
故当扇形的圆心角为时,扇形的面积最大,最大值为.
14.(1);
(2)当时,y的值最大,最大值为.
【分析】(1)根据弧长公式和周长列方程得出关于的函数解析式;
(2)根据面积公式求出关于的函数表达式,根据二次函数性质可得的最大值.
【详解】(1)根据题意,弧的长度为米,弧的长度米,
,
.
(2)依据题意,可知,
化简得:,,
当,.
∴当时,y的值最大,且最大值为.
15.(1);
(2)或.
【分析】由图①可知,以OA为终边的角为+2kπ(k∈Z);以OB为终边的角为+2kπ(k∈Z),由此可求出阴影部分内的角的集合;
由图②可知,以OA为终边的角为+2kπ(k∈Z);以OB为终边的角为+2kπ(k∈Z).
不妨设右边阴影部分所表示的集合为M1,左边阴影部分所表示的集合为M2,由阴影部分内的角的集合为.
【详解】如题图①,以OA为终边的角为+2kπ(k∈Z);以OB为终边的角为+2kπ(k∈Z),
所以阴影部分内的角的集合为
;
如题图②,以OA为终边的角为+2kπ(k∈Z);以OB为终边的角为+2kπ(k∈Z).
不妨设右边阴影部分所表示的集合为M1,左边阴影部分所表示的集合为M2,
则M1=,M2=.
所以阴影部分内的角的集合为
或.
16.小轮转动的角是,弧度,小轮圆周上的点每秒转过的弧长为 cm
【分析】通过相互咬合的两个齿轮转动的齿数相同,得到小轮转动的角度,再通过大轮的转速,得到小轮的转速
【详解】由题意得,相互咬合的两个齿轮,大轮有48齿,小轮有20齿,
所以当大轮旋转一周时,大轮转了48个齿,小轮转了20齿,
所以小轮转动了周,即,,
所以当大轮的转速为150r/min时,小轮的转速为r/min,
所以小轮圆周上的点每秒转过的弧度数为
,
因为小轮的半径为10cm,
所以小轮圆周上的点每秒转过的弧长
cm
答案第1页,共2页
答案第1页,共2页
1.已知一扇形的周长为,则当该扇形的面积取得最大时,圆心角大小为( )
A. B. C.1 D.2
2.若扇形的周长为定值,圆心角为,则当扇形的面积取得最大值时,该扇形的圆心角的值为( )
A.1 B.2 C.3 D.4
3.已知平面上的线段l及点P,任取l上的一点Q,线段PQ长度的最小值称为点P到线段l的距离,记作,若曲线C是边长为4的等边三角形,则点集所表示的图形面积为( )
A. B.
C. D.
4.中国折叠扇有着深厚的文化底蕴.如图(2),在半圆中作出两个扇形和,用扇环形(图中阴影部分)制作折叠扇的扇面.记扇环形的面积为,扇形的面积为,当与的比值为时,扇面的形状较为美观,则此时扇形的半径与半圆的半径之比为
A. B. C. D.
5.“莱洛三角形”是机械学家莱洛研究发现的一种曲边三角形,转子发动机的设计就是利用了莱洛三角形,转子引擎只需转一周,各转子便有一次进气、压缩、点火与排气过程,相当于往复式引擎运转两周,因此具有小排气量就能成就高动力输出的优点.另外,由于转子引擎的轴向运动特性,它不需要精密的曲轴平衡就可以达到非常高的运转转速.“莱洛三角形”是分别以正三角形的顶点为圆心,以其边长为半径作圆弧,由这三段圆弧组成的曲边三角形(如图所示).设“莱洛三角形”曲边上两点之间的最大距离为4,则该“莱洛三角形”的面积为( )
A. B.
C. D.
6.在中,,以为圆心,为半径作圆弧交于点,若弧等分的面积,且弧度,则( )
A. B. C. D.
二、多选题
7.下列说法正确的是( )
A.函数在定义域内为单调递减函数
B.函数与函数的图象关于直线对称
C.已知是第一象限角,那么是第一、三象限的角
D.已知扇形的周长为定值,面积为S,则扇形面积S最大时,扇形的弧所对圆心角为
8.如图,A,B是单位圆上的两个质点,点B 的坐标为(1,0),∠BOA=60°,质点A 以1 rad/s的角速度按逆时针方向在单位圆上运动,质点B 以2 rad/s的角速度按顺时针方向在单位圆上运动,则( )
A.经过1 s后,∠BOA的弧度数为+3
B.经过 s后,扇形AOB的弧长为
C.经过s后,扇形AOB的面积为
D.经过 s后,A,B在单位圆上第一次相遇
三、填空题
9.某设计师为天文馆设计科普宣传图片,其中有一款设计图如图所示.是一个以点O为圆心 长为直径的半圆,.的圆心为P,.与所围的灰色区域即为某天所见的月亮形状,则该月亮形状的面积为___________.
10.我国古代数学著作《九章算术》中《方田》章有弧田面积计算问题,计算术曰:以弦乘矢,矢又自乘,并之,二而一其大意是,弧田面积计算公式为:弧田面积(弦×矢+矢).如图所示的弧田由圆弧和其所对弦围成,公式中“弦”指圆弧所对弦长,“矢”指圆弧顶到弦的距离(等于半径长与圆心到弦的距离之差),现有一圆弧所对圆心角为,弧长为的弧田,按照上述经验公式计算所得弧田面积是______.
11.已知扇形的周长为8cm,则该扇形面积的最大值为________cm2.
12.已知扇形的圆心角为,弧长为,则其面积为___________.
四、解答题
13.已知一个扇形的周长为,求当扇形的圆心角多大时,扇形的面积最大,并求这个最大值.
14.某地政府部门欲做一个“践行核心价值观”的宣传牌,该宣传牌形状是如图所示的扇形环面(由扇形挖去扇形后构成的).已知米,米,线段、线段与弧、弧的长度之和为米,圆心角为弧度.
(1)求关于的函数解析式;
(2)记该宣传牌的面积为,试问取何值时,的值最大 并求出最大值.
15.如图,用弧度表示顶点在原点,始边重合于x轴的非负半轴,终边落在阴影部分内的角的集合(不包括边界).
(1) ;
(2)
16.已知相互咬合的两个齿轮,大轮有48齿,小轮有20齿,当大轮顺时针转动一周时,小轮转动的角是多少度?多少弧度?如果大轮的转速是150r/min,小轮的半径为10cm,那么小轮圆周上的点每秒转过的弧长是多少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据周长建立弧长与半径间的关系,由扇形面积公式可得,利用二次函数求最值,并求出S最大时对应的圆心角即可.
【详解】设扇形的半径为,弧长为,则,
所以,
扇形面积,
当时,有最大值,此时圆心角,
故选:D
2.B
【分析】根据扇形的弧长公式和面积公式,将面积写成关于的表达式,再利用二次函数性质即可求得结果.
【详解】设扇形的半径为,弧长为,
因此,
扇形的面积,
由二次函数性质可知,当时,扇形面积取到最大值;
此时,.
故选:B
3.B
【分析】根据条件可画出满足题意的点集所表示的图形,分别求解区域各个构成部分的面积,进而即得.
【详解】由题意,点集D所表示的图形如图,是边长为4的正三角形,
其中,,,,,
,,
所以扇形的面积为,
,,
,
所以的面积为,
又,
所以四边形的面积为,
又四边形的面积为,
点集所表示的图形面积为:
.
故选:B.
4.B
【解析】扇环形的面积等于扇形的面积减扇形的面积;设半径代入求解.
【详解】设,半圆的半径为,扇形的半径为,
依题意,有,即,
所以,得.
故选:B.
【点睛】本题考查弧度制下扇形面积计算问题.
其解题策思路:
(1)明确弧度制下扇形面积公式,在使用公式时,要注意角的单位必须是弧度.
(2)分析题目已知哪些量、要求哪些量,然后灵活地运用弧长公式、扇形面积公式直接求解,或合理地利用圆心角所在三角形列方程(组)求解.
5.A
【分析】先根据图形特征求得,从而,再求出扇形ABC的面积,最后根据“莱洛三角形”面积与扇形面积之间的关系求出其面积即可.
【详解】解:由题意可知等边三角形的边长为4,即,
所以扇形ABC的面积等于以A为圆心,为半径的圆的面积的,
故扇形ABC的面积,
又,
该“莱洛三角形”的面积为.
故选:A.
6.B
【分析】分析题意,首先设出扇形的半径,表示出扇形的面积和直角三角形的面积,列方程即可求得.
【详解】设扇形的半径为r,则扇形的面积为.
直角三角形POB中,,△POB的面积为.
由题意得,所以.
故选:B
7.BC
【分析】根据单调性判断A选项;根据指数函数与对数函数互为反函数判断B选项;根据角的范围判断C选项;根据扇形面积公式与周长结合二次函数性质求解判断D选项.
【详解】解:对于A选项,函数定义域为,在和上单调递减,在定义域上无单调性,故错误;
对于B选项,指数函数与对数函数互为反函数,图像关于直线对称,故正确;
对于C选项,若是第一象限角,则,故,所以当为偶数时,为第一象限角,为奇数时,为第三象限角,故正确;
对于D选项,由已知,故,所以,故当时,面积最大,此时圆心角,故错误;
故选:BC
8.ABD
【分析】结合条件根据扇形面积,弧长公式逐项分析即得.
【详解】经过1 s后,质点A运动1 rad,质点B运动2 rad,此时∠BOA的弧度数为,故A正确;
经过 s后,,故扇形AOB的弧长为,故B正确;
经过 s后,,故扇形AOB的面积为,故C不正确;
设经过t s后,A,B在单位圆上第一次相遇,则,解得 (s),故D正确.
故选:ABD.
9.
【分析】连接,可得,求出,利用割补法即可求出月牙的面积.
【详解】解:连接,可得,
因为,
所以,,
所以月牙的面积为.
故答案为:.
10.
【分析】由条件根据弧长公式求半径,解直角三角形可得弦、矢的值,求出弧田面积.
【详解】如图:
由题意可得,弧的长为,
所以,故,
在中,可得,,,可得矢,
由,可得弦,
所以弧田面积(弦矢矢.
故答案为:.
11.4
【分析】扇形的周长为, ,,转化为同种变量,利用二次函数最值即可求解.
【详解】设扇形半径为cm,弧长为 cm,则,,所以当时, (cm2).
故答案为:4.
12.
【分析】根据扇形的弧长公式求出半径,再计算扇形的面积.
【详解】扇形的圆心角为,弧长为,
则扇形的半径为r,
面积为.
故答案为:.
13.当扇形的圆心角为时,扇形的面积最大,最大值为.
【分析】设扇形的弧长为,半径为,圆心角为,面积为,可得,由,,可得的范围,根据二次函数的性质求得面积的最大值,再由可得面积取得最大值时的圆心角.
【详解】设扇形的弧长为,半径为,圆心角为,面积为.
由已知,可得,
所以扇形的面积,
因为,,所以,
所以当时,,此时, 所以,
故当扇形的圆心角为时,扇形的面积最大,最大值为.
14.(1);
(2)当时,y的值最大,最大值为.
【分析】(1)根据弧长公式和周长列方程得出关于的函数解析式;
(2)根据面积公式求出关于的函数表达式,根据二次函数性质可得的最大值.
【详解】(1)根据题意,弧的长度为米,弧的长度米,
,
.
(2)依据题意,可知,
化简得:,,
当,.
∴当时,y的值最大,且最大值为.
15.(1);
(2)或.
【分析】由图①可知,以OA为终边的角为+2kπ(k∈Z);以OB为终边的角为+2kπ(k∈Z),由此可求出阴影部分内的角的集合;
由图②可知,以OA为终边的角为+2kπ(k∈Z);以OB为终边的角为+2kπ(k∈Z).
不妨设右边阴影部分所表示的集合为M1,左边阴影部分所表示的集合为M2,由阴影部分内的角的集合为.
【详解】如题图①,以OA为终边的角为+2kπ(k∈Z);以OB为终边的角为+2kπ(k∈Z),
所以阴影部分内的角的集合为
;
如题图②,以OA为终边的角为+2kπ(k∈Z);以OB为终边的角为+2kπ(k∈Z).
不妨设右边阴影部分所表示的集合为M1,左边阴影部分所表示的集合为M2,
则M1=,M2=.
所以阴影部分内的角的集合为
或.
16.小轮转动的角是,弧度,小轮圆周上的点每秒转过的弧长为 cm
【分析】通过相互咬合的两个齿轮转动的齿数相同,得到小轮转动的角度,再通过大轮的转速,得到小轮的转速
【详解】由题意得,相互咬合的两个齿轮,大轮有48齿,小轮有20齿,
所以当大轮旋转一周时,大轮转了48个齿,小轮转了20齿,
所以小轮转动了周,即,,
所以当大轮的转速为150r/min时,小轮的转速为r/min,
所以小轮圆周上的点每秒转过的弧度数为
,
因为小轮的半径为10cm,
所以小轮圆周上的点每秒转过的弧长
cm
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
