人教A版(2019)高中数学必修第二册 6.2.1向量的加法运算(共20张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 6.2.1向量的加法运算(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 385.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 11:55:34 | ||
图片预览


文档简介
(共20张PPT)
6.2.1向量的加法运算
我们知道,数能进行运算。因为有了运算而使数的威力无穷。那么,向量是否也能像数一样进行运算呢?人们从向量的物理背景和数的运算中得到启发,引进向量的运算,本节我们就来研究平面向量的运算,探究其运算性质,体会向量运算的作用。
今天我们先学习向量的加法。
我们知道,位移、力是向量,它们可以合成。能否从位移、力的合成中得到启发,引进向量的加法呢?
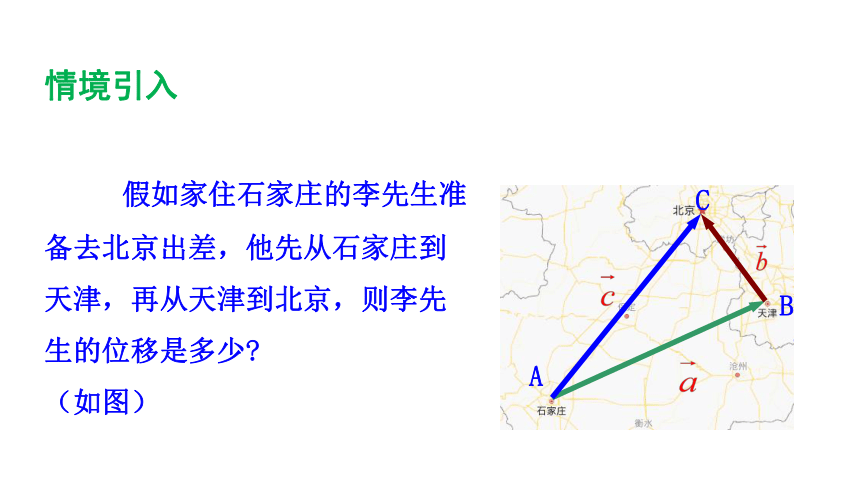
假如家住石家庄的李先生准备去北京出差,他先从石家庄到天津,再从天津到北京,则李先生的位移是多少
(如图)
情境引入
A
B
C
A
B
C
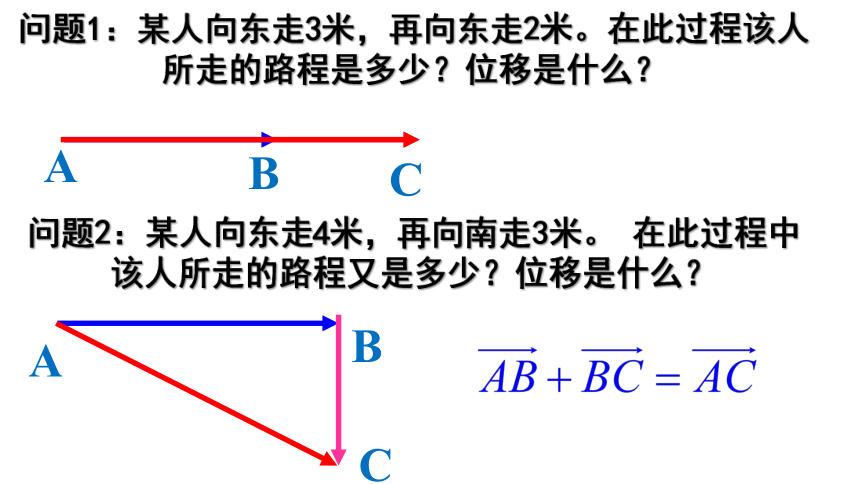
问题1:某人向东走3米,再向东走2米。在此过程该人所走的路程是多少?位移是什么?
A
B
C
问题2:某人向东走4米,再向南走3米。 在此过程中该人所走的路程又是多少?位移是什么?
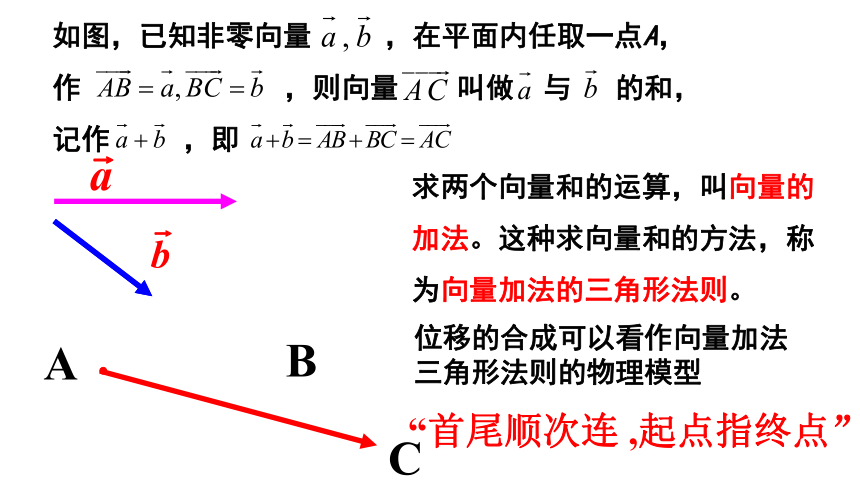
如图,已知非零向量 ,在平面内任取一点A,
作 ,则向量 叫做 与 的和,
记作 ,即
B
C
A
求两个向量和的运算,叫向量的
加法。这种求向量和的方法,称
为向量加法的三角形法则。
位移的合成可以看作向量加法三角形法则的物理模型
“首尾顺次连 ,起点指终点”
B
A
O
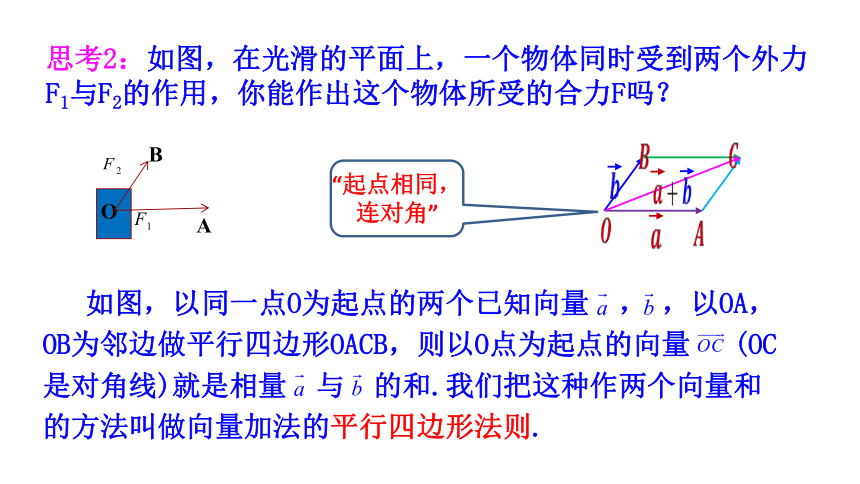
思考2:如图,在光滑的平面上,一个物体同时受到两个外力F1与F2的作用,你能作出这个物体所受的合力F吗?
如图,以同一点O为起点的两个已知向量 , ,以OA,OB为邻边做平行四边形OACB,则以O点为起点的向量 (OC是对角线)就是相量 与 的和.我们把这种作两个向量和的方法叫做向量加法的平行四边形法则.
“起点相同,连对角”
向量的加法
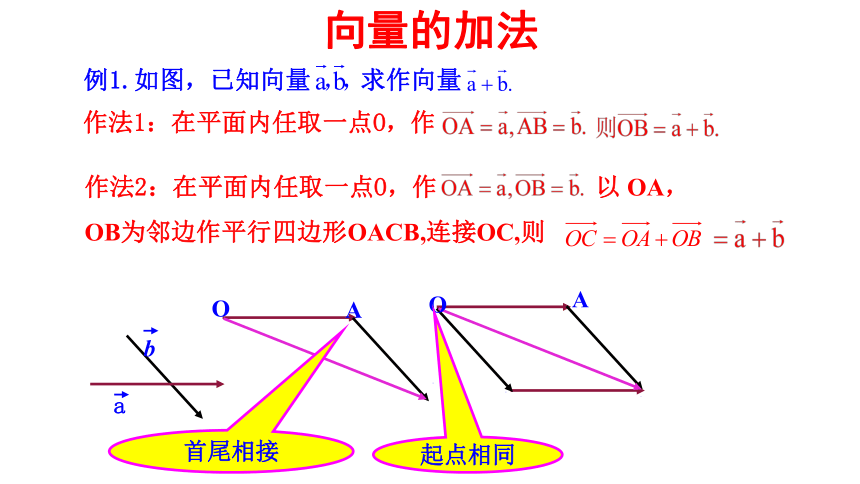
例1.如图,已知向量 求作向量
作法1:在平面内任取一点O,作
作法2:在平面内任取一点O,作 以 OA,OB为邻边作平行四边形OACB,连接OC,则
O
A
B
b
O
A
B
C
a
首尾相接
起点相同
A
B
C
A
B
C
向量的加法
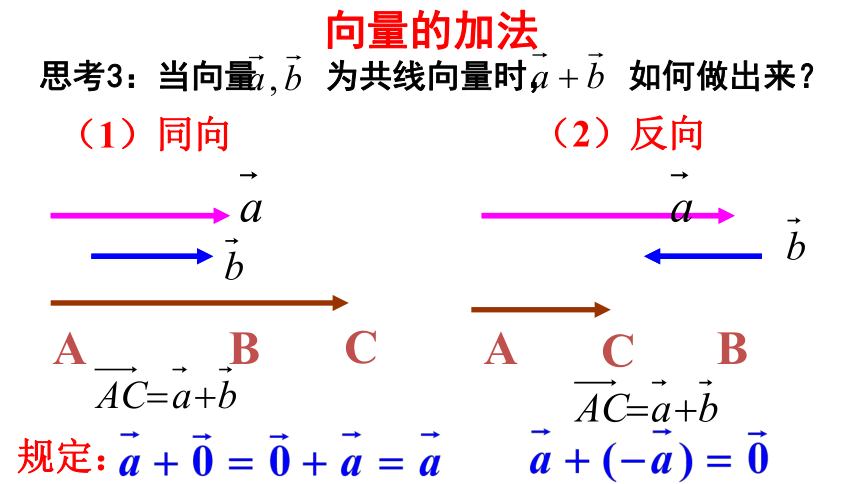
思考3:当向量 为共线向量时, 如何做出来?
规定:
(1)同向
(2)反向
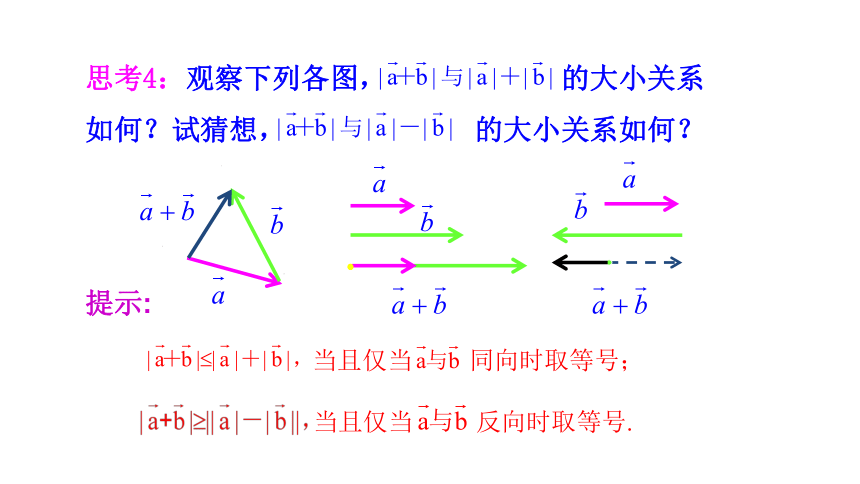
思考4:观察下列各图, 的大小关系
如何?试猜想, 的大小关系如何?
A
B
C
当且仅当 同向时取等号;
当且仅当 反向时取等号.
提示:
当向量 不共线时,和向量的长度 与向量
的长度和 之间的大小关系如何?
三角形的两边之和大于第三边
对于两个非零向量
2.当_______________时,
1.当_______________时,
3.当_______________时,
4.当_______________时,
与 不共线
与 同向
与 反向且
与 反向且
综合以上探究我们可得结论:
思考5:实数的加法运算满足交换律,即对任意a,b∈R,都有a+b=b+a,那么向量的加法也满足交换律吗?如何检验?
B
C
b
A
O
提示:
向量加法的运算律
思考6:实数的加法运算满足结合律,即对任意a,b,c∈R,都有(a+b)+c=a+(b+c).那么向量的加法也满足结合律吗?如何检验?
C
B
A
O
提示:
实数的加法 向量的加法
性 质
A
O
a
b
b
B
a
C
b
a
+
B
b
A
O
a
C
c
b
a
+
+
c
c
b
+
b
a
+
交换律:
结合律:
探究:实数的加法有哪些运算性质?向量的加法是否也满足类似的性质?如果满足,具体形式是什么?
向量加法的多边形法则
向量加法的三角形法则可以推广为多个向量求和的多边形法则,即把每个向量平移,使这些向量首尾相连,则由第一个向量的起点指向最后一个向量终点的向量就是这些向量的和向量.
C
A
B
D
解:设 表示水流的速度, 表示渡船的速度, 表示渡船实际垂直过江的速度。
四边形ABCD为平行四边形
答:渡船要垂直地渡过长江,其航向应为北偏西
例2. 在长江南岸某渡口处,江水以12.5km/h的速度向东流,渡船的速度为25km/h. 渡船要垂直地渡过长江,其航向应如何确定?
在
中
例3.长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如下图所示,一艘船从长江南岸A地出发,垂直于对岸航行,航行速度的大小为15km/h,同时江水的速度为向东6 km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度.
(2)求船实际航行的速度的大小(结果保留小数点后一位)与方向(用与江水速度间的夹角表示,精确到1°).
【解析】(1)如图所示, 表示船速, 表示水速,以AD,AB为邻边作平行四边形ABCD,则 表示船实际航行的速度.
答:船实际航行速度的大小约为16.2km/h,方向与水的流速间的夹角约为68°.
课堂小结
6.2.1向量的加法运算
我们知道,数能进行运算。因为有了运算而使数的威力无穷。那么,向量是否也能像数一样进行运算呢?人们从向量的物理背景和数的运算中得到启发,引进向量的运算,本节我们就来研究平面向量的运算,探究其运算性质,体会向量运算的作用。
今天我们先学习向量的加法。
我们知道,位移、力是向量,它们可以合成。能否从位移、力的合成中得到启发,引进向量的加法呢?
假如家住石家庄的李先生准备去北京出差,他先从石家庄到天津,再从天津到北京,则李先生的位移是多少
(如图)
情境引入
A
B
C
A
B
C
问题1:某人向东走3米,再向东走2米。在此过程该人所走的路程是多少?位移是什么?
A
B
C
问题2:某人向东走4米,再向南走3米。 在此过程中该人所走的路程又是多少?位移是什么?
如图,已知非零向量 ,在平面内任取一点A,
作 ,则向量 叫做 与 的和,
记作 ,即
B
C
A
求两个向量和的运算,叫向量的
加法。这种求向量和的方法,称
为向量加法的三角形法则。
位移的合成可以看作向量加法三角形法则的物理模型
“首尾顺次连 ,起点指终点”
B
A
O
思考2:如图,在光滑的平面上,一个物体同时受到两个外力F1与F2的作用,你能作出这个物体所受的合力F吗?
如图,以同一点O为起点的两个已知向量 , ,以OA,OB为邻边做平行四边形OACB,则以O点为起点的向量 (OC是对角线)就是相量 与 的和.我们把这种作两个向量和的方法叫做向量加法的平行四边形法则.
“起点相同,连对角”
向量的加法
例1.如图,已知向量 求作向量
作法1:在平面内任取一点O,作
作法2:在平面内任取一点O,作 以 OA,OB为邻边作平行四边形OACB,连接OC,则
O
A
B
b
O
A
B
C
a
首尾相接
起点相同
A
B
C
A
B
C
向量的加法
思考3:当向量 为共线向量时, 如何做出来?
规定:
(1)同向
(2)反向
思考4:观察下列各图, 的大小关系
如何?试猜想, 的大小关系如何?
A
B
C
当且仅当 同向时取等号;
当且仅当 反向时取等号.
提示:
当向量 不共线时,和向量的长度 与向量
的长度和 之间的大小关系如何?
三角形的两边之和大于第三边
对于两个非零向量
2.当_______________时,
1.当_______________时,
3.当_______________时,
4.当_______________时,
与 不共线
与 同向
与 反向且
与 反向且
综合以上探究我们可得结论:
思考5:实数的加法运算满足交换律,即对任意a,b∈R,都有a+b=b+a,那么向量的加法也满足交换律吗?如何检验?
B
C
b
A
O
提示:
向量加法的运算律
思考6:实数的加法运算满足结合律,即对任意a,b,c∈R,都有(a+b)+c=a+(b+c).那么向量的加法也满足结合律吗?如何检验?
C
B
A
O
提示:
实数的加法 向量的加法
性 质
A
O
a
b
b
B
a
C
b
a
+
B
b
A
O
a
C
c
b
a
+
+
c
c
b
+
b
a
+
交换律:
结合律:
探究:实数的加法有哪些运算性质?向量的加法是否也满足类似的性质?如果满足,具体形式是什么?
向量加法的多边形法则
向量加法的三角形法则可以推广为多个向量求和的多边形法则,即把每个向量平移,使这些向量首尾相连,则由第一个向量的起点指向最后一个向量终点的向量就是这些向量的和向量.
C
A
B
D
解:设 表示水流的速度, 表示渡船的速度, 表示渡船实际垂直过江的速度。
四边形ABCD为平行四边形
答:渡船要垂直地渡过长江,其航向应为北偏西
例2. 在长江南岸某渡口处,江水以12.5km/h的速度向东流,渡船的速度为25km/h. 渡船要垂直地渡过长江,其航向应如何确定?
在
中
例3.长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如下图所示,一艘船从长江南岸A地出发,垂直于对岸航行,航行速度的大小为15km/h,同时江水的速度为向东6 km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度.
(2)求船实际航行的速度的大小(结果保留小数点后一位)与方向(用与江水速度间的夹角表示,精确到1°).
【解析】(1)如图所示, 表示船速, 表示水速,以AD,AB为邻边作平行四边形ABCD,则 表示船实际航行的速度.
答:船实际航行速度的大小约为16.2km/h,方向与水的流速间的夹角约为68°.
课堂小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
