湘教版数学八年级下册课件1.3 直角三角形全等的判定 第2课时 (共14张PPT)
文档属性
| 名称 | 湘教版数学八年级下册课件1.3 直角三角形全等的判定 第2课时 (共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 857.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-07 20:04:48 | ||
图片预览





文档简介
(共14张PPT)
本课内容
本节内容
1.3
第2课时
湘教版数学 八年级下册
直角三角形全等的斜边、直角边定理是:
斜边、直角边定理 有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
使用“HL”定理要注意哪些问题?
直角三角形全等的判定定理:SAS,AAS,ASA,SSS,HL
综上所述,直角三角形全等的判定条件可归纳为:
一边及一个锐角对应相等的两个直角三角形全等;
两边对应相等的两个直角三角形全等;
切记!!!
两边及其中一边的对角对应相等的 两个三角形不一定全等。
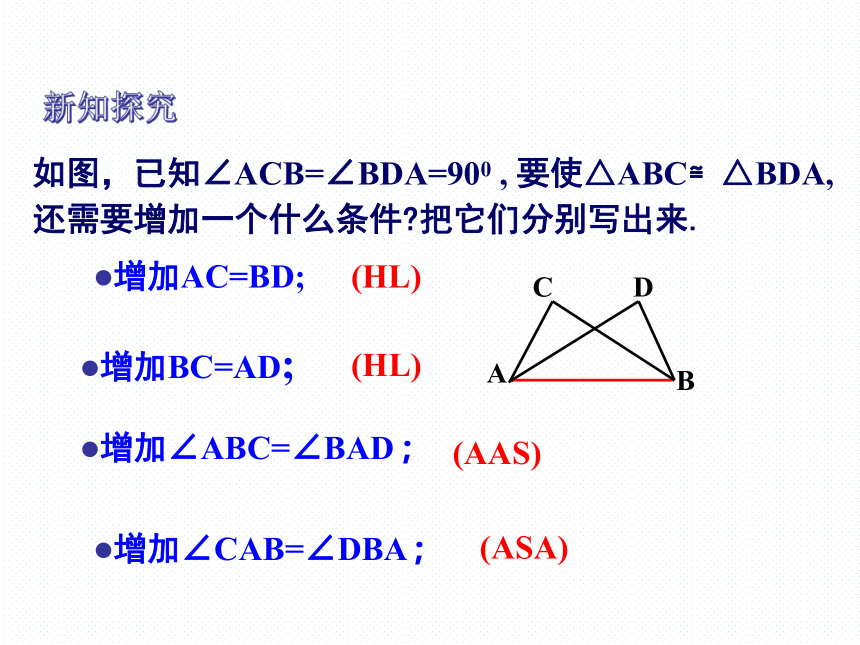
如图,已知∠ACB=∠BDA=900 , 要使△ABC≌△BDA,
还需要增加一个什么条件 把它们分别写出来.
D
C
B
A
增加AC=BD;
增加BC=AD;
增加∠ABC=∠BAD ;
增加∠CAB=∠DBA ;
(HL)
(HL)
(AAS)
(ASA)
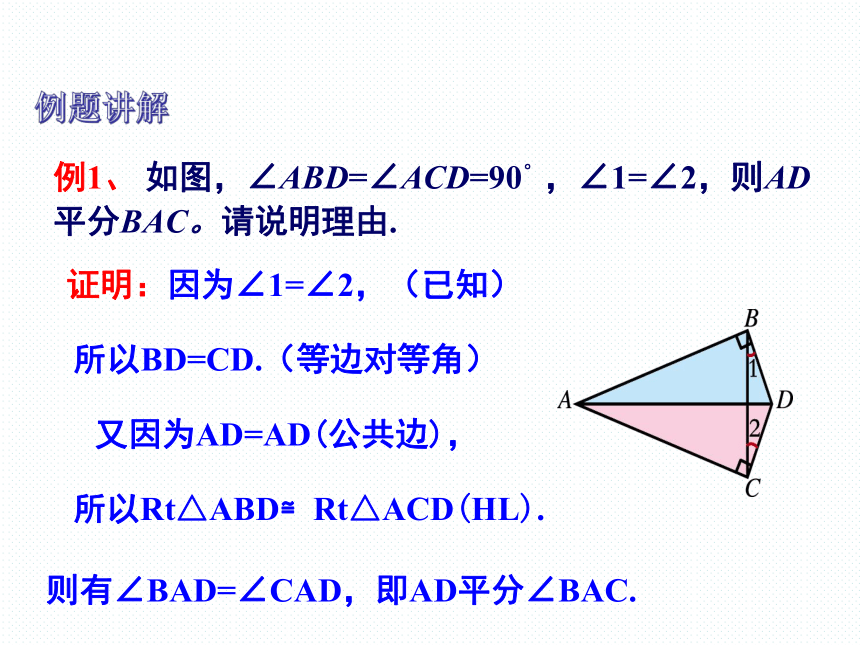
例1、 如图,∠ABD=∠ACD=90°,∠1=∠2,则AD
平分BAC。请说明理由.
则有∠BAD=∠CAD,即AD平分∠BAC.
证明:因为∠1=∠2,(已知)
所以BD=CD.(等边对等角)
又因为AD=AD(公共边),
所以Rt△ABD≌Rt△ACD(HL).
变式训练:如图,已知P是∠AOB内部一点,PD⊥OA, PE⊥OB,D,E分别是垂足,且PD=PE,则点P在∠AOB的平分线上。请说明理由。
A
B
P
O
D
E
提示:连接OP,
再证明 Rt△ODP≌Rt△OEP
∠DOP=∠EOP
证明过程学生独立完成。
【方法总结】在运用HL判定两个直角三角形全等时,
要紧紧抓住直角边和斜边这两个要点.
例2、已知如图AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别为E、F.求证:CE=DF.
分析:根据已知条件证明现有的Rt△ABC与Rt△BAD全等,得出线段和角相等,再证Rt△ACE和Rt△BDF全等,从而解决问题.
【方法总结】一般三角形全等的判定方法仍然适用于直角三角形,因此判定直角三角形全等的方法有五种,不要只限于“HL”.
先用“HL”证得:Rt△ABC≌Rt△BAD,
得:AC=BD,∠CAB=∠DBA
再用“AAS”证得:△CAE≌△DBF,∴CE=DF.
例3、已知,如图所示,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
△ABD≌△CAE,∴BD=AE,AD=CE,
∵AE=AD+DE,∴BD=CE+DE.
【方法总结】当看到题目中要证线段和差关系时,而且这三边分别在两个全等三角形中时,可先判定两三角形全等,再证明线段关系.在证明全等时可灵活选用判定方法.
分析:先证△ABD≌△ACE,再根据等量代换得出结论.
1、已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF.
求证: △ABC是等腰三角形.
2、如图,已知CE ⊥ AB,DF ⊥ AB,AC=BD,AF=BE,则CE=DF。请说明理由。AC∥BD吗?为什么?
F
E
D
C
B
A
D
B
C
A
F
E
证明 △BDF≌△CDE
∠B=∠C,从而结论得证。
由AF=BE,可得:AE=BF
可证得 △AEC≌△BFD,得:CE=DF
∠A=∠B, 得:AC∥BD 。
3、如图,CD⊥AB,BE⊥AC,垂足分别是
D、E, BE、CD相交于点O,如果AB=AC
哪么图中有几对全等的直角三角形?取其
中的一对予以证明。
E
D
C
B
A
O
4、已知:如图,AB=CD,AE⊥BD,CF ⊥BD,垂足分别为
E、F,且BF=DE.求证: ∠ABD= ∠CDB.
F
E
D
C
B
A
3对直角三角形全等。
由BF=DE,可得:BE=DF
可证得 △AEB≌△CFD,
得: ∠ABD= ∠CDB
还能得到哪些结论?
5. 已知:AB⊥AC,CD⊥AC,AD=CB, 问△ABC 与
△CDA全等吗 AD//BC 吗?
D
C
B
A
A
B
C
D
6.如图,在 ABC和 BCD 中,已知AC⊥BC,AD⊥BD ,垂足分别为C、D ,AC=BD 求证:BC=AD
AC边公共,由“HL”可证得:
△ABC≌△CDA,
得:∠DAC= ∠BCA,∴AD//BC
AB边公共,由“HL”可证得:
△ACB≌△BDA,
∴BC=AD
7、已知AB//CD, ∠A=90 °、AB=CE、BC=DE,试问DE与BC的位置关系是怎样的?
B
E
D
C
A
M
1
2
证明:∵AB//CD, ∠A=90°
∴∠DCA=180°-∠A=90°
在Rt ABC和Rt CED中,
∵ AB=CE ,BC=DE
∴Rt ABC≌Rt CED
∴∠1= ∠D
∠1+ ∠2= ∠2+ ∠D=90°
∴∠EMC=90°. 即:DE⊥BC
答:DE⊥BC
1、如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系?
可证得: △ABC≌△DEF,
得:∠ABC= ∠DEF,
又:∠DFE+∠DEF=900
∴ ∠DFE+∠ABC=900
即:∠ABC与∠DFE互余。
2、如图,在△ABC与△A B C 中, CD, C D 分别是高,并且AC=A C,CD=C D,∠ACB=∠A C B.
求证:△ABC≌△A B C .
′
′
′
′
′
′
′
′
′
′
′
′
′
′
′
B
C
D
A
′
A
′
B
′
C
′
D
先可证得: △ABD≌△A C D (HL)
′
′
′
得:∠A= ∠A,
′
可证得: △ABC≌△A B C (ASA)
′
′
′
再加AC=A C , ∠ACB= ∠A C B
′
′
′
′
′
通过这节课的学习你有何收获?
直角三角形的全等判定方法:(四条)
概括为两条:
一边及一个锐角对应相等的两个直角三角形全等;
两边对应相等的两个直角三角形全等;
特别注意“HL”定理的使用条件.
有斜边和一条直角边对应相等的两个直角三角形全等.
作业:p21 A 3 B 5、6
本课内容
本节内容
1.3
第2课时
湘教版数学 八年级下册
直角三角形全等的斜边、直角边定理是:
斜边、直角边定理 有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
使用“HL”定理要注意哪些问题?
直角三角形全等的判定定理:SAS,AAS,ASA,SSS,HL
综上所述,直角三角形全等的判定条件可归纳为:
一边及一个锐角对应相等的两个直角三角形全等;
两边对应相等的两个直角三角形全等;
切记!!!
两边及其中一边的对角对应相等的 两个三角形不一定全等。
如图,已知∠ACB=∠BDA=900 , 要使△ABC≌△BDA,
还需要增加一个什么条件 把它们分别写出来.
D
C
B
A
增加AC=BD;
增加BC=AD;
增加∠ABC=∠BAD ;
增加∠CAB=∠DBA ;
(HL)
(HL)
(AAS)
(ASA)
例1、 如图,∠ABD=∠ACD=90°,∠1=∠2,则AD
平分BAC。请说明理由.
则有∠BAD=∠CAD,即AD平分∠BAC.
证明:因为∠1=∠2,(已知)
所以BD=CD.(等边对等角)
又因为AD=AD(公共边),
所以Rt△ABD≌Rt△ACD(HL).
变式训练:如图,已知P是∠AOB内部一点,PD⊥OA, PE⊥OB,D,E分别是垂足,且PD=PE,则点P在∠AOB的平分线上。请说明理由。
A
B
P
O
D
E
提示:连接OP,
再证明 Rt△ODP≌Rt△OEP
∠DOP=∠EOP
证明过程学生独立完成。
【方法总结】在运用HL判定两个直角三角形全等时,
要紧紧抓住直角边和斜边这两个要点.
例2、已知如图AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别为E、F.求证:CE=DF.
分析:根据已知条件证明现有的Rt△ABC与Rt△BAD全等,得出线段和角相等,再证Rt△ACE和Rt△BDF全等,从而解决问题.
【方法总结】一般三角形全等的判定方法仍然适用于直角三角形,因此判定直角三角形全等的方法有五种,不要只限于“HL”.
先用“HL”证得:Rt△ABC≌Rt△BAD,
得:AC=BD,∠CAB=∠DBA
再用“AAS”证得:△CAE≌△DBF,∴CE=DF.
例3、已知,如图所示,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
△ABD≌△CAE,∴BD=AE,AD=CE,
∵AE=AD+DE,∴BD=CE+DE.
【方法总结】当看到题目中要证线段和差关系时,而且这三边分别在两个全等三角形中时,可先判定两三角形全等,再证明线段关系.在证明全等时可灵活选用判定方法.
分析:先证△ABD≌△ACE,再根据等量代换得出结论.
1、已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF.
求证: △ABC是等腰三角形.
2、如图,已知CE ⊥ AB,DF ⊥ AB,AC=BD,AF=BE,则CE=DF。请说明理由。AC∥BD吗?为什么?
F
E
D
C
B
A
D
B
C
A
F
E
证明 △BDF≌△CDE
∠B=∠C,从而结论得证。
由AF=BE,可得:AE=BF
可证得 △AEC≌△BFD,得:CE=DF
∠A=∠B, 得:AC∥BD 。
3、如图,CD⊥AB,BE⊥AC,垂足分别是
D、E, BE、CD相交于点O,如果AB=AC
哪么图中有几对全等的直角三角形?取其
中的一对予以证明。
E
D
C
B
A
O
4、已知:如图,AB=CD,AE⊥BD,CF ⊥BD,垂足分别为
E、F,且BF=DE.求证: ∠ABD= ∠CDB.
F
E
D
C
B
A
3对直角三角形全等。
由BF=DE,可得:BE=DF
可证得 △AEB≌△CFD,
得: ∠ABD= ∠CDB
还能得到哪些结论?
5. 已知:AB⊥AC,CD⊥AC,AD=CB, 问△ABC 与
△CDA全等吗 AD//BC 吗?
D
C
B
A
A
B
C
D
6.如图,在 ABC和 BCD 中,已知AC⊥BC,AD⊥BD ,垂足分别为C、D ,AC=BD 求证:BC=AD
AC边公共,由“HL”可证得:
△ABC≌△CDA,
得:∠DAC= ∠BCA,∴AD//BC
AB边公共,由“HL”可证得:
△ACB≌△BDA,
∴BC=AD
7、已知AB//CD, ∠A=90 °、AB=CE、BC=DE,试问DE与BC的位置关系是怎样的?
B
E
D
C
A
M
1
2
证明:∵AB//CD, ∠A=90°
∴∠DCA=180°-∠A=90°
在Rt ABC和Rt CED中,
∵ AB=CE ,BC=DE
∴Rt ABC≌Rt CED
∴∠1= ∠D
∠1+ ∠2= ∠2+ ∠D=90°
∴∠EMC=90°. 即:DE⊥BC
答:DE⊥BC
1、如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系?
可证得: △ABC≌△DEF,
得:∠ABC= ∠DEF,
又:∠DFE+∠DEF=900
∴ ∠DFE+∠ABC=900
即:∠ABC与∠DFE互余。
2、如图,在△ABC与△A B C 中, CD, C D 分别是高,并且AC=A C,CD=C D,∠ACB=∠A C B.
求证:△ABC≌△A B C .
′
′
′
′
′
′
′
′
′
′
′
′
′
′
′
B
C
D
A
′
A
′
B
′
C
′
D
先可证得: △ABD≌△A C D (HL)
′
′
′
得:∠A= ∠A,
′
可证得: △ABC≌△A B C (ASA)
′
′
′
再加AC=A C , ∠ACB= ∠A C B
′
′
′
′
′
通过这节课的学习你有何收获?
直角三角形的全等判定方法:(四条)
概括为两条:
一边及一个锐角对应相等的两个直角三角形全等;
两边对应相等的两个直角三角形全等;
特别注意“HL”定理的使用条件.
有斜边和一条直角边对应相等的两个直角三角形全等.
作业:p21 A 3 B 5、6
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
