湘教版数学八年级下册 1.4 角平分线的性质 (第1课时) 课件(共13张PPT)
文档属性
| 名称 | 湘教版数学八年级下册 1.4 角平分线的性质 (第1课时) 课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 871.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 07:56:06 | ||
图片预览


文档简介
(共13张PPT)
本课内容
本节内容
1.4
角平分线的性质
第1课时
湘教版数学 八年级下册
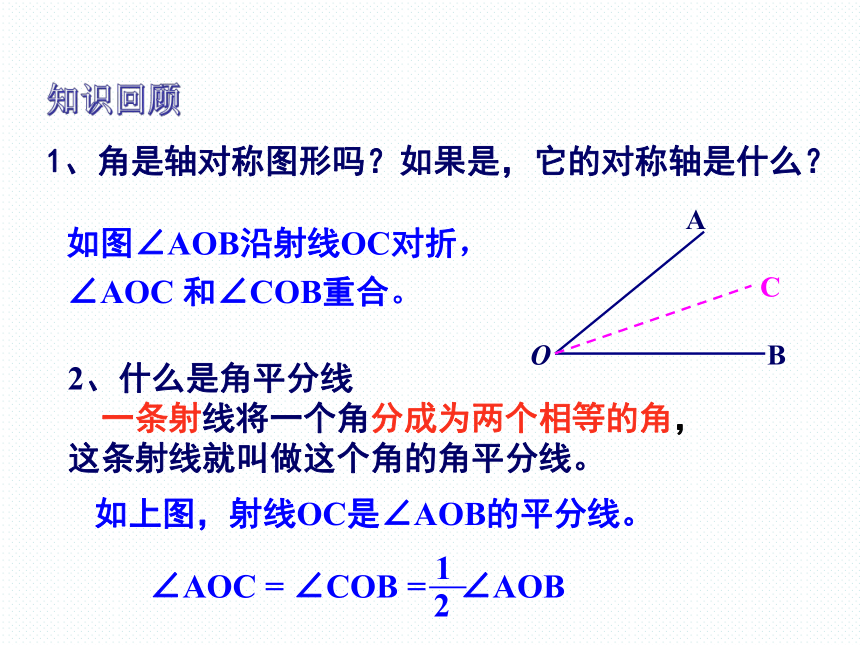
1、角是轴对称图形吗?如果是,它的对称轴是什么?
2、什么是角平分线
一条射线将一个角分成为两个相等的角,
这条射线就叫做这个角的角平分线。
如图∠AOB沿射线OC对折,
∠AOC 和∠COB重合。
A
B
O
C
如上图,射线OC是∠AOB的平分线。
∠AOC = ∠COB = ∠AOB
1
2
2.分别以MN为圆心.大于 MN的长为半径作
弧.两弧在∠AOB的内部交于C.
1
2
A
B
O
M
N
C
你能证明吗?
3、用尺规作已知角的平分线:
作法:1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
3.作射线OC.
射线OC即为所求.
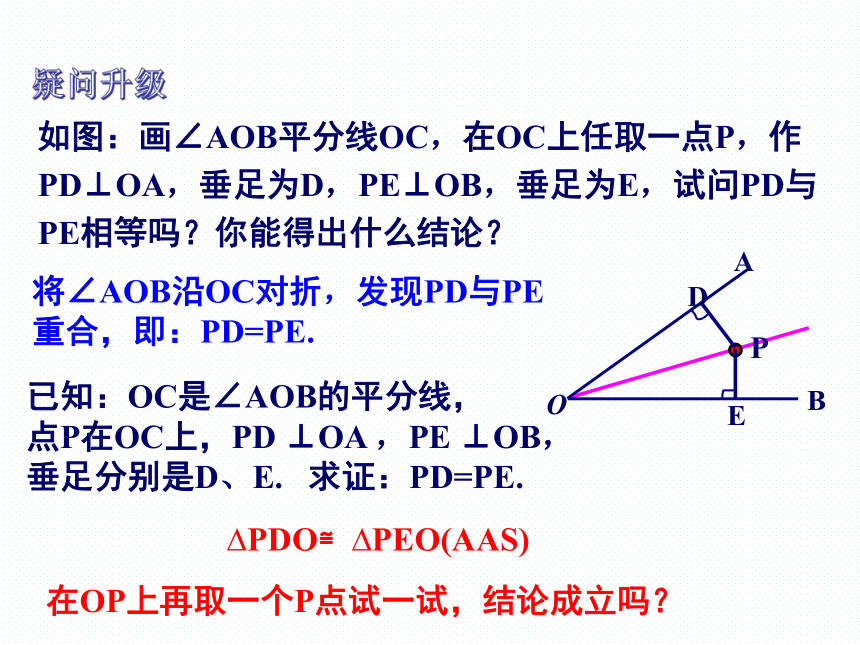
如图:画∠AOB平分线OC,在OC上任取一点P,作
PD⊥OA,垂足为D,PE⊥OB,垂足为E,试问PD与
PE相等吗?你能得出什么结论?
A
O
B
P
E
D
PDO≌ PEO(AAS)
在OP上再取一个P点试一试,结论成立吗?
将∠AOB沿OC对折,发现PD与PE重合,即:PD=PE.
已知:OC是∠AOB的平分线,
点P在OC上,PD ⊥OA ,PE ⊥OB,
垂足分别是D、E. 求证:PD=PE.
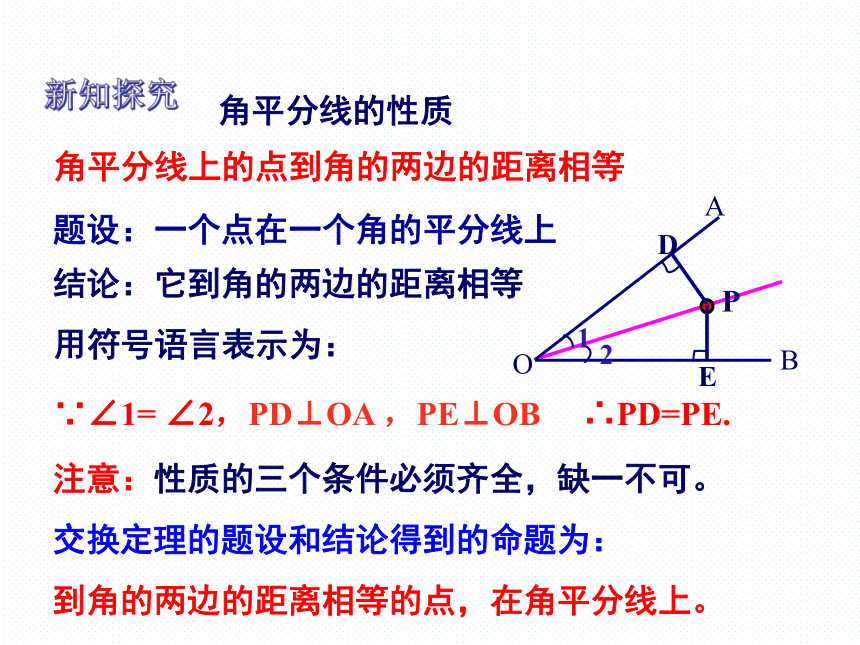
角平分线上的点到角的两边的距离相等
题设:一个点在一个角的平分线上
结论:它到角的两边的距离相等
用符号语言表示为:
∵∠1= ∠2,PD⊥OA ,PE⊥OB ∴PD=PE.
交换定理的题设和结论得到的命题为:
A
O
B
P
E
D
1
2
到角的两边的距离相等的点,在角平分线上。
角平分线的性质
注意:性质的三个条件必须齐全,缺一不可。
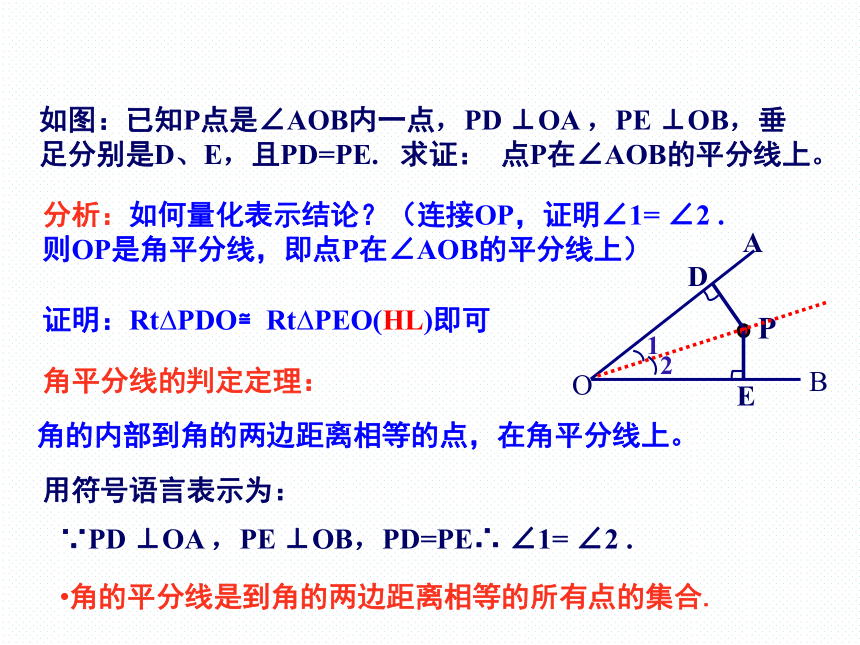
角的内部到角的两边距离相等的点,在角平分线上。
角平分线的判定定理:
用符号语言表示为:
∵PD ⊥OA ,PE ⊥OB,PD=PE∴ ∠1= ∠2 .
A
O
B
P
E
D
分析:如何量化表示结论?(连接OP,证明∠1= ∠2 .
则OP是角平分线,即点P在∠AOB的平分线上)
证明:Rt PDO≌Rt PEO(HL)即可
角的平分线是到角的两边距离相等的所有点的集合.
1
2
如图:已知P点是∠AOB内一点,PD ⊥OA ,PE ⊥OB,垂足分别是D、E,且PD=PE. 求证: 点P在∠AOB的平分线上。
1、如图,∠BAD= ∠BCD=900 ,∠1= ∠2 .
(1)求证:点B在∠ADC的平分线上 .
(2)求证:BD是∠ABC的平分线 .
1
2
D
C
A
B
证明:(1) ∵∠1= ∠2 ∴ BA=BC,
∴点B在∠ADC的平分线上
(2)在Rt BAD和Rt BCD中,
∵ BA=BC BD=BD
∴ Rt BAD≌Rt BCD (HL)
∠ABD= ∠CBD
∴ BD是∠ABC的平分线
∵∠BAD= ∠BCD=900, BA ⊥AD,BC ⊥CD
例2、如图,在Rt△ABC 中,∠C=90°,BD是∠AB C的平分线 ,DE⊥AB,垂足为E,图中相等的线段有哪些?为什么?
∵ ∠C=90° (已知)
∴ DC⊥BC(垂直的定义)
又∵ BD是∠ABC的平分线
∵ DE⊥BA(已知)
∴ DE=DC(角平分线上的任意点到角的两边的距离相等)
答: (1) DE=DC
(2) BE=BC
角平分线的性质,为我们证明两线段相等 又提供了新的方法与途径
A
B
C
D
E
1
2
3
4
做完本题后,你对角平分线,又增加了什么认识
1、填空:
(1) ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(____________________________________)
(2) ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
( )
A
C
D
E
B
1
2
∠1= ∠2
DC=DE
到角的两边的距离相等的点在角平分线上。
角平分线上的点到角的两边的距离相等
(3)如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线交BC于D,BC=15,且DB=10,则点D到AB的距离为 。
5
E
D
A
C
B
(3)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ BD = CD , ( )
√
D
C
B
A
(2)∵ 如图,DC⊥AC,DB⊥AB (已知)
∴ BD = CD,( )
D
C
B
A
2、判断以下所填结论是否正确:
×
(1)∵ 如图,AD平分∠BAC(已知)
∴ BD= CD ( )
A
D
C
B
×
3.如图,△ABC中,∠A=90°,BD平分∠ABC,AD=6,BC=16,DE⊥BC,求△BDC面积。
∴ DE=AD=6(角平分线上的任意点
到角的两边的距离相等)
E
D
B
A
C
解:∵ ∠A=90° (已知)
∴ DA⊥AB(垂直的定义)
又∵ BD是∠ABC的平分线
∵ DE⊥BA DE⊥BC(已知)
S△DBC = BC×DE= ×16×6=48
1
2
1
2
4.已知:如图,∠C=∠D=90° ,AC=AD .
求证:(1) ∠ABC= ∠ABD ;
(2)BC=BD.(要求不用三角形全等的判定)
B
D
A
C
证明: (1)∵∠C= ∠D=90°,
∴ BAD和 BCD均为直角三角形,
又∵AC= AD,AB=AB
∴Rt BAD≌Rt BCD (HL)
∴∠ABC= ∠ABD
(2)由(1)得: ∠CAB= ∠DAB
即:AB是∠CAD的平分线
∵∠C= ∠D=90°,即:BC⊥AC,BD⊥AD
∴ BC=BD
1.角平分线的性质定理:
在角平分线上的点到角的两边的距离相等
2.角平分线的判定定理:
到一个角的两边的距离相等的点,在这个角平分线上。
3.角平分线的性质定理和角平分线的判定定理是证明角相等、线段相等的新途径.
4.通过这节课的学习,觉得自己有什么收获吗?
一定要“悟”到点东西,纳入到自己的认知结构中去.
作业:p24 练习 p26 A 1、2
本课内容
本节内容
1.4
角平分线的性质
第1课时
湘教版数学 八年级下册
1、角是轴对称图形吗?如果是,它的对称轴是什么?
2、什么是角平分线
一条射线将一个角分成为两个相等的角,
这条射线就叫做这个角的角平分线。
如图∠AOB沿射线OC对折,
∠AOC 和∠COB重合。
A
B
O
C
如上图,射线OC是∠AOB的平分线。
∠AOC = ∠COB = ∠AOB
1
2
2.分别以MN为圆心.大于 MN的长为半径作
弧.两弧在∠AOB的内部交于C.
1
2
A
B
O
M
N
C
你能证明吗?
3、用尺规作已知角的平分线:
作法:1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
3.作射线OC.
射线OC即为所求.
如图:画∠AOB平分线OC,在OC上任取一点P,作
PD⊥OA,垂足为D,PE⊥OB,垂足为E,试问PD与
PE相等吗?你能得出什么结论?
A
O
B
P
E
D
PDO≌ PEO(AAS)
在OP上再取一个P点试一试,结论成立吗?
将∠AOB沿OC对折,发现PD与PE重合,即:PD=PE.
已知:OC是∠AOB的平分线,
点P在OC上,PD ⊥OA ,PE ⊥OB,
垂足分别是D、E. 求证:PD=PE.
角平分线上的点到角的两边的距离相等
题设:一个点在一个角的平分线上
结论:它到角的两边的距离相等
用符号语言表示为:
∵∠1= ∠2,PD⊥OA ,PE⊥OB ∴PD=PE.
交换定理的题设和结论得到的命题为:
A
O
B
P
E
D
1
2
到角的两边的距离相等的点,在角平分线上。
角平分线的性质
注意:性质的三个条件必须齐全,缺一不可。
角的内部到角的两边距离相等的点,在角平分线上。
角平分线的判定定理:
用符号语言表示为:
∵PD ⊥OA ,PE ⊥OB,PD=PE∴ ∠1= ∠2 .
A
O
B
P
E
D
分析:如何量化表示结论?(连接OP,证明∠1= ∠2 .
则OP是角平分线,即点P在∠AOB的平分线上)
证明:Rt PDO≌Rt PEO(HL)即可
角的平分线是到角的两边距离相等的所有点的集合.
1
2
如图:已知P点是∠AOB内一点,PD ⊥OA ,PE ⊥OB,垂足分别是D、E,且PD=PE. 求证: 点P在∠AOB的平分线上。
1、如图,∠BAD= ∠BCD=900 ,∠1= ∠2 .
(1)求证:点B在∠ADC的平分线上 .
(2)求证:BD是∠ABC的平分线 .
1
2
D
C
A
B
证明:(1) ∵∠1= ∠2 ∴ BA=BC,
∴点B在∠ADC的平分线上
(2)在Rt BAD和Rt BCD中,
∵ BA=BC BD=BD
∴ Rt BAD≌Rt BCD (HL)
∠ABD= ∠CBD
∴ BD是∠ABC的平分线
∵∠BAD= ∠BCD=900, BA ⊥AD,BC ⊥CD
例2、如图,在Rt△ABC 中,∠C=90°,BD是∠AB C的平分线 ,DE⊥AB,垂足为E,图中相等的线段有哪些?为什么?
∵ ∠C=90° (已知)
∴ DC⊥BC(垂直的定义)
又∵ BD是∠ABC的平分线
∵ DE⊥BA(已知)
∴ DE=DC(角平分线上的任意点到角的两边的距离相等)
答: (1) DE=DC
(2) BE=BC
角平分线的性质,为我们证明两线段相等 又提供了新的方法与途径
A
B
C
D
E
1
2
3
4
做完本题后,你对角平分线,又增加了什么认识
1、填空:
(1) ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(____________________________________)
(2) ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
( )
A
C
D
E
B
1
2
∠1= ∠2
DC=DE
到角的两边的距离相等的点在角平分线上。
角平分线上的点到角的两边的距离相等
(3)如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线交BC于D,BC=15,且DB=10,则点D到AB的距离为 。
5
E
D
A
C
B
(3)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ BD = CD , ( )
√
D
C
B
A
(2)∵ 如图,DC⊥AC,DB⊥AB (已知)
∴ BD = CD,( )
D
C
B
A
2、判断以下所填结论是否正确:
×
(1)∵ 如图,AD平分∠BAC(已知)
∴ BD= CD ( )
A
D
C
B
×
3.如图,△ABC中,∠A=90°,BD平分∠ABC,AD=6,BC=16,DE⊥BC,求△BDC面积。
∴ DE=AD=6(角平分线上的任意点
到角的两边的距离相等)
E
D
B
A
C
解:∵ ∠A=90° (已知)
∴ DA⊥AB(垂直的定义)
又∵ BD是∠ABC的平分线
∵ DE⊥BA DE⊥BC(已知)
S△DBC = BC×DE= ×16×6=48
1
2
1
2
4.已知:如图,∠C=∠D=90° ,AC=AD .
求证:(1) ∠ABC= ∠ABD ;
(2)BC=BD.(要求不用三角形全等的判定)
B
D
A
C
证明: (1)∵∠C= ∠D=90°,
∴ BAD和 BCD均为直角三角形,
又∵AC= AD,AB=AB
∴Rt BAD≌Rt BCD (HL)
∴∠ABC= ∠ABD
(2)由(1)得: ∠CAB= ∠DAB
即:AB是∠CAD的平分线
∵∠C= ∠D=90°,即:BC⊥AC,BD⊥AD
∴ BC=BD
1.角平分线的性质定理:
在角平分线上的点到角的两边的距离相等
2.角平分线的判定定理:
到一个角的两边的距离相等的点,在这个角平分线上。
3.角平分线的性质定理和角平分线的判定定理是证明角相等、线段相等的新途径.
4.通过这节课的学习,觉得自己有什么收获吗?
一定要“悟”到点东西,纳入到自己的认知结构中去.
作业:p24 练习 p26 A 1、2
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
