湘教版数学八年级下册 1.4 角平分线的性质( 第2课时) 课件(共13张PPT)
文档属性
| 名称 | 湘教版数学八年级下册 1.4 角平分线的性质( 第2课时) 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 851.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 00:00:00 | ||
图片预览

文档简介
(共13张PPT)
本课内容
本节内容
1.4
角平分线的性质
第2课时
湘教版数学 八年级下册
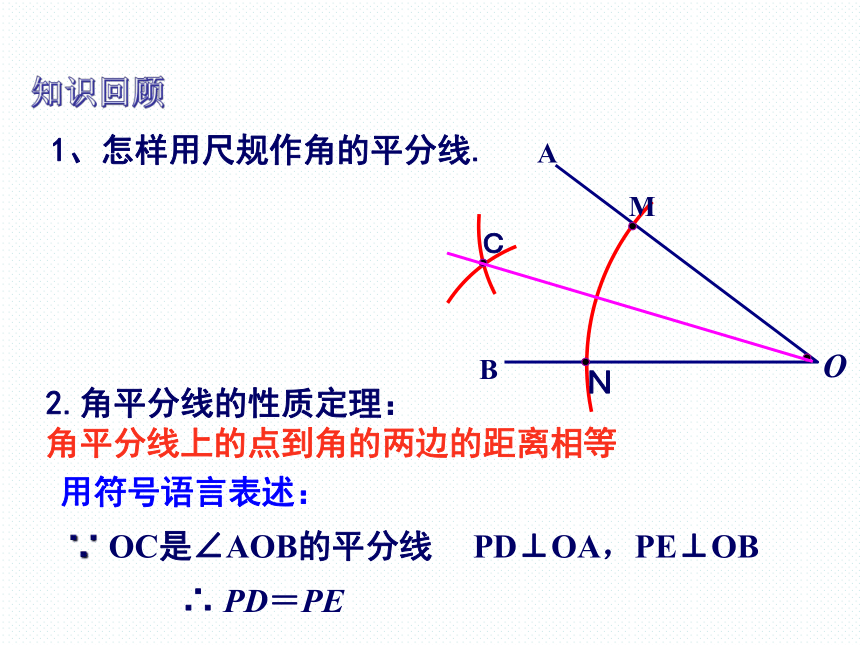
1、怎样用尺规作角的平分线.
2.角平分线的性质定理:
角平分线上的点到角的两边的距离相等
A
B
O
M
N
C
PD⊥OA,PE⊥OB
∵ OC是∠AOB的平分线
∴ PD=PE
用符号语言表述:
O
C
B
1
A
2
P
D
E
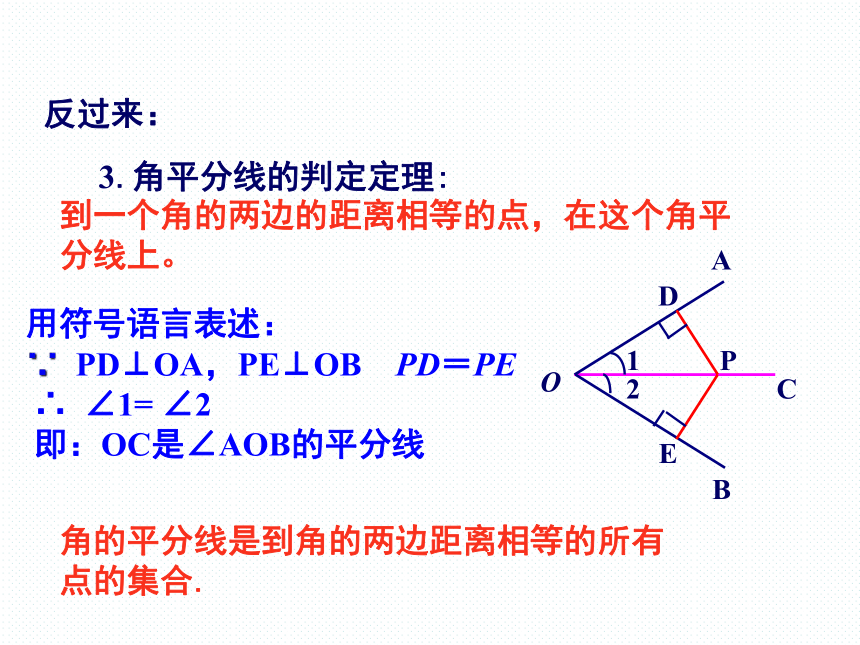
3.角平分线的判定定理:
到一个角的两边的距离相等的点,在这个角平分线上。
用符号语言表述:
∵ PD⊥OA,PE⊥OB PD=PE
∴ ∠1= ∠2
即:OC是∠AOB的平分线
反过来:
角的平分线是到角的两边距离相等的所有点的集合.
A
C
B
M
N
P
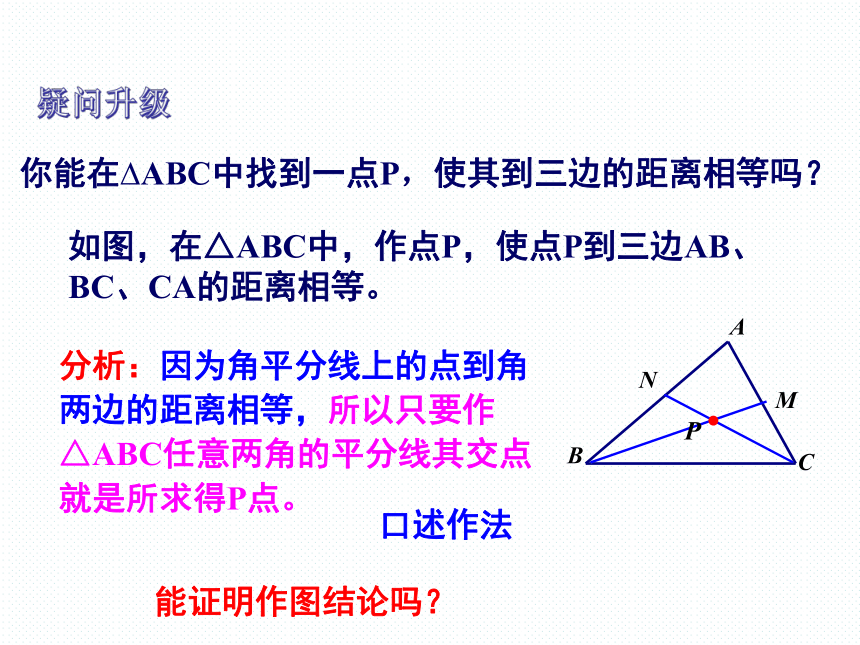
如图,在△ABC中,作点P,使点P到三边AB、BC、CA的距离相等。
你能在 ABC中找到一点P,使其到三边的距离相等吗?
分析:因为角平分线上的点到角两边的距离相等,所以只要作△ABC任意两角的平分线其交点就是所求得P点。
口述作法
能证明作图结论吗?
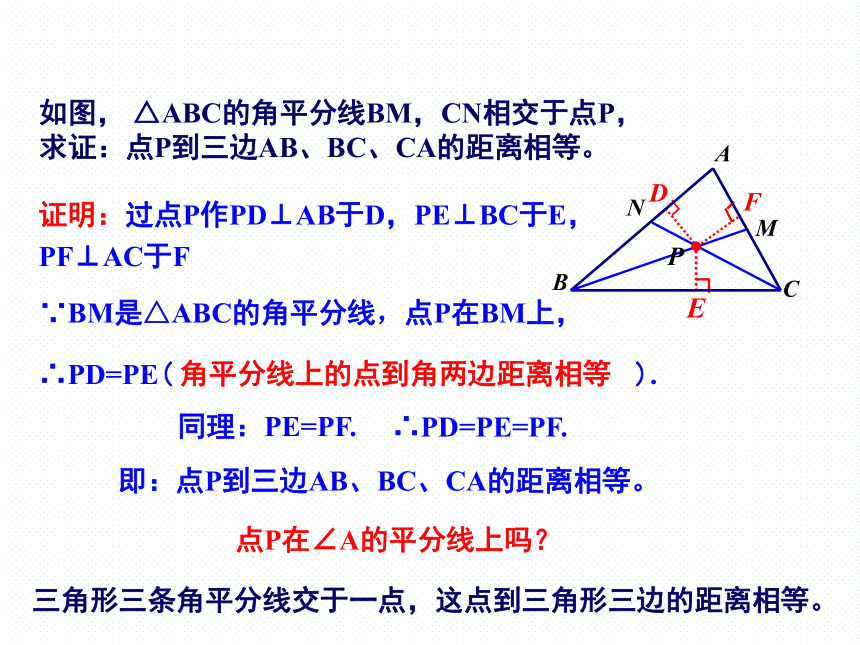
如图, △ABC的角平分线BM,CN相交于点P,求证:点P到三边AB、BC、CA的距离相等。
D
E
F
A
C
B
M
N
P
证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F
∵BM是△ABC的角平分线,点P在BM上,
同理:PE=PF.
∴PD=PE=PF.
即:点P到三边AB、BC、CA的距离相等。
点P在∠A的平分线上吗?
三角形三条角平分线交于一点,这点到三角形三边的距离相等。
∴PD=PE( ).
角平分线上的点到角两边距离相等
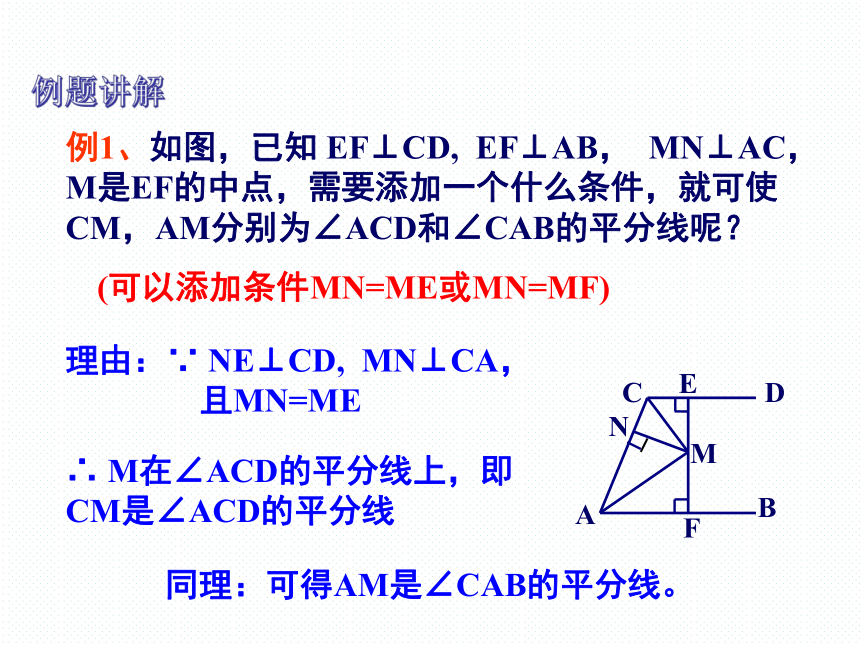
例1、如图,已知 EF⊥CD, EF⊥AB, MN⊥AC, M是EF的中点,需要添加一个什么条件,就可使CM,AM分别为∠ACD和∠CAB的平分线呢?
(可以添加条件MN=ME或MN=MF)
理由:∵ NE⊥CD, MN⊥CA,
且MN=ME
N
M
F
E
D
C
B
A
∴ M在∠ACD的平分线上,即CM是∠ACD的平分线
同理:可得AM是∠CAB的平分线。
例2、 如图,在△ABC的外角∠DAC的平分线上任取一点P,作PE⊥DB,PF⊥AC,垂足分别为点E、F。试探索BE+PF与PB的大小关系。
A
C
P
B
F
E
D
解:∵AP是∠DAC的平分线。
又 PE⊥DB PF⊥AC
∴ PE=PF
在 EBP中,BE+PE>PB
∴ BE+PF>PB
例3、如图,已知△ABC的外角∠CBD和∠BCE的
平分线相交于点F,求证:点F在∠DAE的平分线上.
证明:过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M
G
H
M
∵点F在∠BCE的平分线上,FG⊥AE, FM⊥BC
∴FG=FM
又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC
∴FM=FH
∴FG=FH
∴点F在∠DAE的平分线上
A
B
C
D
E
F
F
E
D
C
B
A
D
N
E
B
F
M
C
A
1、如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。
求证:AD是△ABC的角平分线。
提示:Rt△DEB ≌Rt△DFC(HL)
得:DE=DF
由角平分线性质,得出结论。
2、已知 BD⊥AM于点D,CE⊥AN于点E,BD,CE交点F,CF=BF,
求证:点F在∠A的平分线上.
提示:Rt△FEB ≌Rt△FDC(AAS)
得:DE=EF
由角平分线性质,得出结论。
D
C
B
A
变式训练:如图,△ABC中,∠A = 90°,AB = AC,
BD是∠BAC的平分线,DE⊥BC于E,若BC = 10cm,
则△DCE的周长等于( )
A.10cm B.8cm C.6cm D.9cm
E
A
3、已知:如图,在△ABC中,∠A=90°,
AB = AC,BD平分∠ABC. 求证:BC = AB + AD
提示:由角平分线性质,得:AD=DE.
Rt△BAD≌Rt△BED(HL)
得:AB=BE
又可证:△DEC是等腰直角三角形,DE=EC
如图,有两条河流l1,l2 ,两个工厂A,B,现要在这个区域内建一个中转站P,要求P到两工厂的距离相等,同时到两河流的距离也相等,请你在图中标出P点的位置。
解:(1)画AB的垂直平分线MN,
A
B
l1
l2
(2)画∠α的平分线交直线MN于P,
则P点就是中转站的位置。
P
变式:如图,某地要在三条公路围成的一块平地上修建一个超市.使这个超市到三条公路的距离相等,应在何处修建
在确定超市的位置时,一定要画出三个角的平分线吗
你是怎样思考的
你是如何证明的
若把限制条件去掉,修建超市的地址有几处?
到角的两边的距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
用数学语言表示为:
角的平分线上的点到角的两边的距离相等.
∵ QD⊥OA,QE⊥OB,
点Q在∠AOB的平分线上
∴ QD=QE
作业:P25 练习 P26 习题 3、5
本课内容
本节内容
1.4
角平分线的性质
第2课时
湘教版数学 八年级下册
1、怎样用尺规作角的平分线.
2.角平分线的性质定理:
角平分线上的点到角的两边的距离相等
A
B
O
M
N
C
PD⊥OA,PE⊥OB
∵ OC是∠AOB的平分线
∴ PD=PE
用符号语言表述:
O
C
B
1
A
2
P
D
E
3.角平分线的判定定理:
到一个角的两边的距离相等的点,在这个角平分线上。
用符号语言表述:
∵ PD⊥OA,PE⊥OB PD=PE
∴ ∠1= ∠2
即:OC是∠AOB的平分线
反过来:
角的平分线是到角的两边距离相等的所有点的集合.
A
C
B
M
N
P
如图,在△ABC中,作点P,使点P到三边AB、BC、CA的距离相等。
你能在 ABC中找到一点P,使其到三边的距离相等吗?
分析:因为角平分线上的点到角两边的距离相等,所以只要作△ABC任意两角的平分线其交点就是所求得P点。
口述作法
能证明作图结论吗?
如图, △ABC的角平分线BM,CN相交于点P,求证:点P到三边AB、BC、CA的距离相等。
D
E
F
A
C
B
M
N
P
证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F
∵BM是△ABC的角平分线,点P在BM上,
同理:PE=PF.
∴PD=PE=PF.
即:点P到三边AB、BC、CA的距离相等。
点P在∠A的平分线上吗?
三角形三条角平分线交于一点,这点到三角形三边的距离相等。
∴PD=PE( ).
角平分线上的点到角两边距离相等
例1、如图,已知 EF⊥CD, EF⊥AB, MN⊥AC, M是EF的中点,需要添加一个什么条件,就可使CM,AM分别为∠ACD和∠CAB的平分线呢?
(可以添加条件MN=ME或MN=MF)
理由:∵ NE⊥CD, MN⊥CA,
且MN=ME
N
M
F
E
D
C
B
A
∴ M在∠ACD的平分线上,即CM是∠ACD的平分线
同理:可得AM是∠CAB的平分线。
例2、 如图,在△ABC的外角∠DAC的平分线上任取一点P,作PE⊥DB,PF⊥AC,垂足分别为点E、F。试探索BE+PF与PB的大小关系。
A
C
P
B
F
E
D
解:∵AP是∠DAC的平分线。
又 PE⊥DB PF⊥AC
∴ PE=PF
在 EBP中,BE+PE>PB
∴ BE+PF>PB
例3、如图,已知△ABC的外角∠CBD和∠BCE的
平分线相交于点F,求证:点F在∠DAE的平分线上.
证明:过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M
G
H
M
∵点F在∠BCE的平分线上,FG⊥AE, FM⊥BC
∴FG=FM
又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC
∴FM=FH
∴FG=FH
∴点F在∠DAE的平分线上
A
B
C
D
E
F
F
E
D
C
B
A
D
N
E
B
F
M
C
A
1、如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。
求证:AD是△ABC的角平分线。
提示:Rt△DEB ≌Rt△DFC(HL)
得:DE=DF
由角平分线性质,得出结论。
2、已知 BD⊥AM于点D,CE⊥AN于点E,BD,CE交点F,CF=BF,
求证:点F在∠A的平分线上.
提示:Rt△FEB ≌Rt△FDC(AAS)
得:DE=EF
由角平分线性质,得出结论。
D
C
B
A
变式训练:如图,△ABC中,∠A = 90°,AB = AC,
BD是∠BAC的平分线,DE⊥BC于E,若BC = 10cm,
则△DCE的周长等于( )
A.10cm B.8cm C.6cm D.9cm
E
A
3、已知:如图,在△ABC中,∠A=90°,
AB = AC,BD平分∠ABC. 求证:BC = AB + AD
提示:由角平分线性质,得:AD=DE.
Rt△BAD≌Rt△BED(HL)
得:AB=BE
又可证:△DEC是等腰直角三角形,DE=EC
如图,有两条河流l1,l2 ,两个工厂A,B,现要在这个区域内建一个中转站P,要求P到两工厂的距离相等,同时到两河流的距离也相等,请你在图中标出P点的位置。
解:(1)画AB的垂直平分线MN,
A
B
l1
l2
(2)画∠α的平分线交直线MN于P,
则P点就是中转站的位置。
P
变式:如图,某地要在三条公路围成的一块平地上修建一个超市.使这个超市到三条公路的距离相等,应在何处修建
在确定超市的位置时,一定要画出三个角的平分线吗
你是怎样思考的
你是如何证明的
若把限制条件去掉,修建超市的地址有几处?
到角的两边的距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
用数学语言表示为:
角的平分线上的点到角的两边的距离相等.
∵ QD⊥OA,QE⊥OB,
点Q在∠AOB的平分线上
∴ QD=QE
作业:P25 练习 P26 习题 3、5
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
