16.1 二次根式(2)(共20张PPT)沪科版数学八年级下册课件
文档属性
| 名称 | 16.1 二次根式(2)(共20张PPT)沪科版数学八年级下册课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 297.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 13:11:25 | ||
图片预览








文档简介
(共20张PPT)
16.1 二次根式 (2)
通过上一节课的学习,凭着自己已
掌握的知识,说说对二次根式 的理解!
知识回顾
2. a可以是数,也可以是式子.
3. 形式上含有二次根号
5.既可表示开方运算,也可表示运算的结果.
1. 表示a的算术平方根.
4. a≥0, ≥0
( 双重非负性)
如: 这类代数式只能称为含有二次根式的代数式,不能称之为二次根式;
而 这类代数式,应把 这些二次根式看作系数或常数项,整个代数式仍看做整式。
你知道吗?
下列各式是二次根式吗
(m≤0),
(x,y 异号)
在实数范围内,负数没有平方根
情境引入
二次根式的性质(1)
新知探究
二次根式的性质(2)
试一试,计算:
想一想 等于什么 请举例验证.
=
=
=
3
5
2
0.04
性质2:
a
-a
|a|
0
2
2
3
3
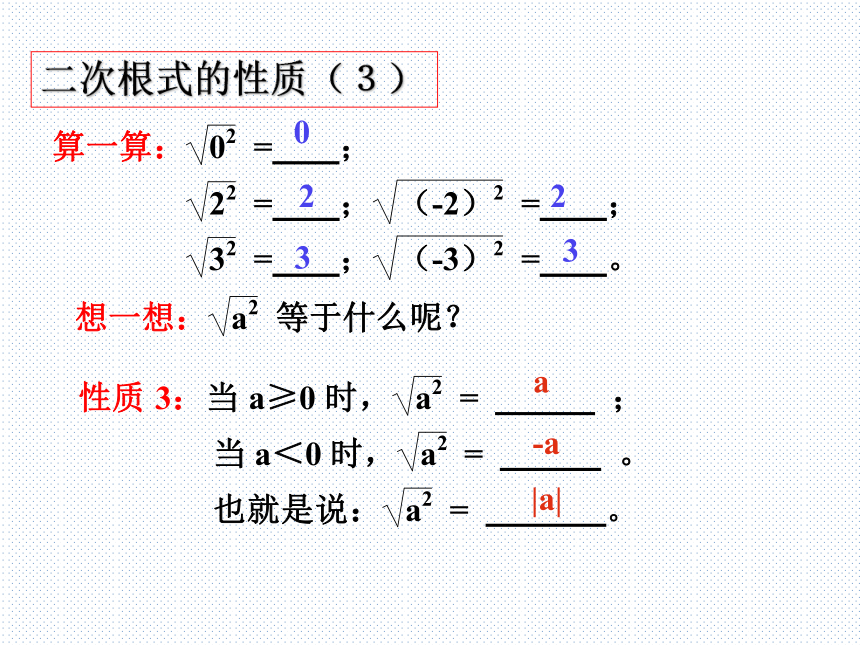
二次根式的性质(3)
由 ,可以得 。
利用这个式子,可以把任何一个非负数写成带有“ ”的形式,例:
a
0
-a
( a >0 )
( a =0 )
( a <0 )
归纳
知识迁移
知识梳理
2.从取值范围来看,
a≥ 0
a取任何实
1.从运算顺序来看,
先开方,后平方。
先平方,后开方。
3.从运算结果来看:
=a
a (a≥ 0)
-a (a<0)
=
=∣a∣
比较分析 和
读法
运算顺序
a的取值范围
运算结果
先开方,后平方
先平方,后开方
a≥0
a取全体实数
a
∣a∣
根号a的平方
根号下a平方
例 化简及求值:
(1) (2) (3) (a<0,b>0)
(4) , 其中a=
(5)
新知探究
=-ab
其中a=
1.计算下列各题:
(1)
(2)
2.若 ,则x的取值范围为 ( )
A. x≤1 B. x≥1 C. 0≤x≤1 D.一切有理数
与 是一样的吗?
你的理由是什么,请小组讨论一下。
√
a
( )
2
随堂练习
-1
3
(-5)×2×(-2)=20
若a,b为实数,且
求 的值。
解:
16.1 二次根式 (2)
通过上一节课的学习,凭着自己已
掌握的知识,说说对二次根式 的理解!
知识回顾
2. a可以是数,也可以是式子.
3. 形式上含有二次根号
5.既可表示开方运算,也可表示运算的结果.
1. 表示a的算术平方根.
4. a≥0, ≥0
( 双重非负性)
如: 这类代数式只能称为含有二次根式的代数式,不能称之为二次根式;
而 这类代数式,应把 这些二次根式看作系数或常数项,整个代数式仍看做整式。
你知道吗?
下列各式是二次根式吗
(m≤0),
(x,y 异号)
在实数范围内,负数没有平方根
情境引入
二次根式的性质(1)
新知探究
二次根式的性质(2)
试一试,计算:
想一想 等于什么 请举例验证.
=
=
=
3
5
2
0.04
性质2:
a
-a
|a|
0
2
2
3
3
二次根式的性质(3)
由 ,可以得 。
利用这个式子,可以把任何一个非负数写成带有“ ”的形式,例:
a
0
-a
( a >0 )
( a =0 )
( a <0 )
归纳
知识迁移
知识梳理
2.从取值范围来看,
a≥ 0
a取任何实
1.从运算顺序来看,
先开方,后平方。
先平方,后开方。
3.从运算结果来看:
=a
a (a≥ 0)
-a (a<0)
=
=∣a∣
比较分析 和
读法
运算顺序
a的取值范围
运算结果
先开方,后平方
先平方,后开方
a≥0
a取全体实数
a
∣a∣
根号a的平方
根号下a平方
例 化简及求值:
(1) (2) (3) (a<0,b>0)
(4) , 其中a=
(5)
新知探究
=-ab
其中a=
1.计算下列各题:
(1)
(2)
2.若 ,则x的取值范围为 ( )
A. x≤1 B. x≥1 C. 0≤x≤1 D.一切有理数
与 是一样的吗?
你的理由是什么,请小组讨论一下。
√
a
( )
2
随堂练习
-1
3
(-5)×2×(-2)=20
若a,b为实数,且
求 的值。
解:
