9.2 用样本估计总体——2022-2023学年高一数学人教A版2019必修第二册同步课时训练(含答案)
文档属性
| 名称 | 9.2 用样本估计总体——2022-2023学年高一数学人教A版2019必修第二册同步课时训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 252.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 00:00:00 | ||
图片预览



文档简介
9.2 用样本估计总体——2022-2023学年高一数学人教A版2019必修第二册同步课时训练
1.据某地区气象局发布的气象数据,末来某十天内该地区每天最高温度(单位:℃)分别为:31,29,24,27,26,25,24,26,26,23,则这组数据的第40百分位数为( )
A.27 B.26.5 C.25.5 D.25
2.已知样本数据2,4,6,a的平均数为4,则该样本的标准差是( )
A. B. C.2 D.
3.已知某7个数的平均数为4,方差为2,现加入一个新数据4,此时这8个数的平均数为,方差为,则( )
A. B.
C. D.
4.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是( )
A.中位数 B.平均数 C.方差 D.极差
5.某校进行了一次创新作文大赛,共有100名同学参赛,经过评判,这100名参赛者的得分都在之间,其得分的频率分布直方图如图,则下列结论错误的是( )
A.得分在之间的共有40人
B.从这100名参赛者中随机选取1人,其得分在的概率为0.5
C.估计得分的众数为55
D.这100名参赛者得分的中位数为65
6.某学习小组在一次数学测验中,得100分的有1人,95分的有1人,90分的有2人,85分的有4人,80分和75分的各有1人,则该小组成绩的平均数、众数、中位数分别是( )
A.85,85,85 B.87,85,86 C.87,85,85 D.87,85,90
7.对于数据3,3,2,3,6,3,10,3,6,3,2.有下列说法:
①这组数据的众数是3;
②这组数据的众数与中位数的数值不相等;
③这组数据的中位数与平均数的数值相等;
④这组数据的平均数与众数的数值相等.
其中正确的个数是( )
A.1 B.2 C.3 D.4
8. (多选)中华人民共和国第十四届全国运动会于2021年9月15日在陕西西安开幕.某射击运动员为了在全运会上取得优异成绩,积极训练备战,在某次训练中,该运动员连续射击10次的成绩(单位:环)依次为7,8,8,,6,10,7,9,8,9,因记录员工作失误,有一个数被污染了,但记录员记得这组数据的平均数为8.在去掉其中的一个最高成绩和一个最低成绩后,以下结论正确的是( )
A.众数不变 B.中位数不变 C.极差不变 D.平均数不变
9. (多选)某班有50名学生,其中男生30名,随机询问了该班5名男生和5名女生在某次数学测验中的成绩.5名男生的成绩分别为86,94,88,92,90,5名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( )
A.这种抽样方法是简单随机抽样 B.这5名男生成绩的中位数小于这5名女生成绩的中位数 C.这5名男生成绩的方差大于这5名女生成绩的方差 D.该班男生成绩的平均数小于该班女生成绩的平均数
10. (多选)已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11,若这组数据的平均数与众数的和是中位数的2倍,则丢失的数据可能是( )
A. B.4 C.12 D.18
11.从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为_________.
分数 5 4 3 2 1
人数 20 10 30 30 10
12.某高校有甲、乙两个数学建模兴趣班.其中甲班有40人,乙班有50人.现分析两个班的一次考试成绩,算得甲班的平均成绩是90分,乙班的平均成绩是81分,则该校数学建模兴趣班的平均成绩是________________分.
13.去年,相关部门对某城市“五朵金花”之一的某景区在“十一”黄金周中每天的游客人数作了统计,其频率分布如下表所示:
时间 10月1日 10月2日 10月3日 10月4日 10月5日 10月6日 10月7日
频率 0.05 0.08 0.09 0.13 0.30 0.15 0.20
已知10月1日这天该景区的营业额约为8万元,假定这七天每天游客人均消费相同,则这个黄金周该景区游客数量最多的那一天的营业额约为____________万元.
14.某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图.
(2)估计这次考试的及格率(60分及以上为及格),众数和中位数.(保留整数)
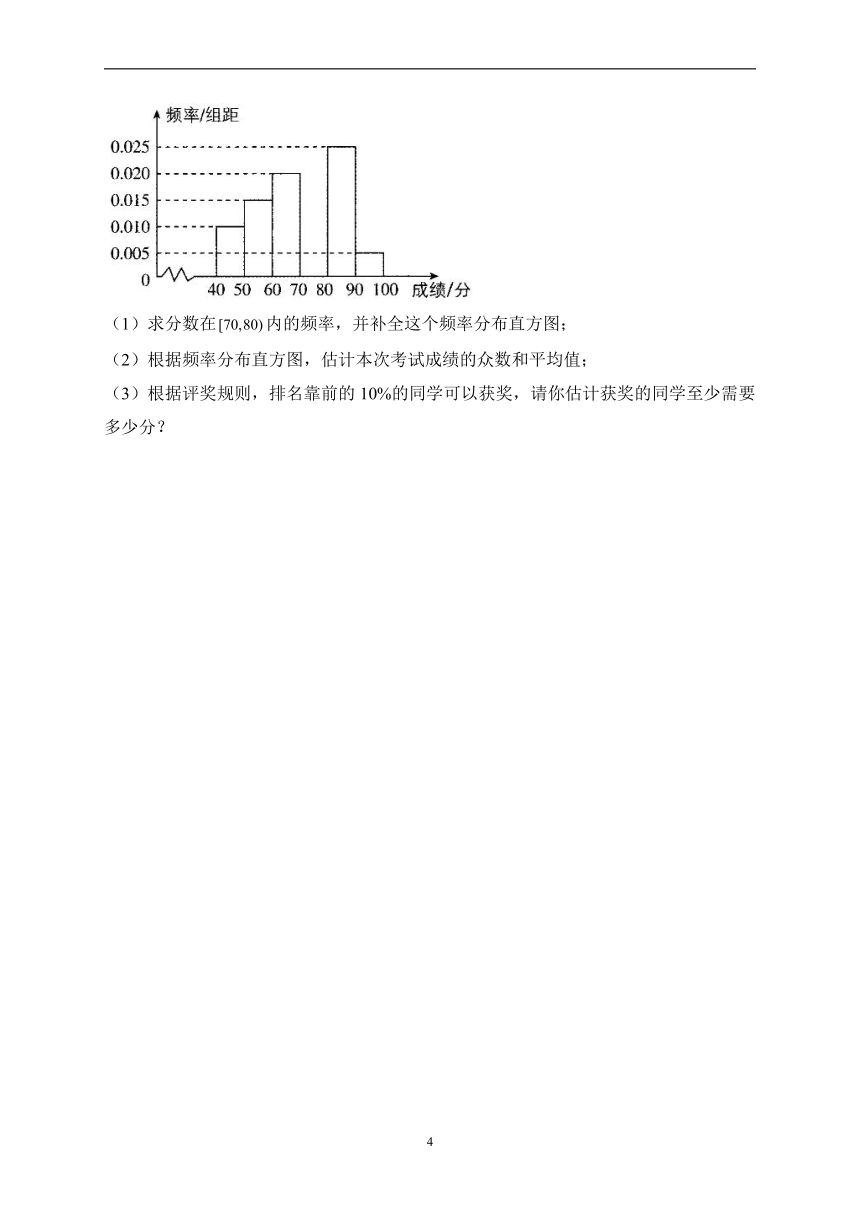
15.为了解某市参加2018年全国高中数学联赛的学生的考试成绩,现从中选取60名同学,将其成绩(百分制,均为正数)分成,,,,,六组后,得到部分频率分布直方图(如图),回答下列问题.
(1)求分数在内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,估计本次考试成绩的众数和平均值;
(3)根据评奖规则,排名靠前的10%的同学可以获奖,请你估计获奖的同学至少需要多少分?
答案以及解析
1.答案:C
解析:第一步:按从小到大排列原始数据先将这些数据按照从小到大进行排序,分别为23,24,24,25,26,26,26,27,29,31,
第二步:计算
计算得,
第三步:得结果
因此该组数据的第40百分位数为.
2.答案:B
解析:因为2,4,6,a的平均数为4,所以,得,所以该样本的标准差,故选B.
3.答案:A
解析:某7 个数的平均数为4,方差为2,则这8个数的平均数为,方差为. 故选:A.
4.答案:A
解析:设9位评委评分按从小到大排列为.
则①原始中位数为,去掉最低分,最高分,后剩余,
中位数仍为,A正确.
②原始平均数,后来平均数
平均数受极端值影响较大,与不一定相同,B不正确
③
由②易知,C不正确.
④原极差,后来极差显然极差变小,D不正确.
5.答案:D
解析:根据频率和为1,计算,解得,得分在的频率是0.40,估计得分在的有(人),A正确;
得分在的频率为0.5,可得这100名参赛者中随机选取一人,得分在的概率为0.5,B正确;
根据频率分布直方图知,最高的小矩形对应的底边中点为,即估计得分众数为55,C正确;
中位数的估计值为,解得,故D错,故选D.
6.答案:C
解析:依题意,将该小组所有数学成绩从小到大列出:75,80,85,85,85,85,90,90,95,100,观察知众数和中位数均为85,计算得平均数为87.
7.答案:A
解析:在这11个数据中,数据3出现了6次,频率最高,故众数是3,①正确;将这11个数据按从小到大排列得2,2,3,3,3,3,3,3,6,6,10,最中间的数据是3,故中位数是3,②错误;这组数据的平均数,故③④错误.故选A.
8.答案:ABD
解析:设被污染的数为a,由这组数据的平均数,解得.这10个数据中8出现了4次,出现的次数最多,所以众数是8.将这10个数据按从小到大的顺序排列,为6,7,7,8,8,8,8,9,9,10,中位数应是第5和第6个数的平均数,即.这组数据中最大的为10,最小的为6,故极差为.去掉其中的一个最大数10和一个最小数6后的8个数据中,众数仍为8,中位数还是8,平均数为8,极差为,所以A,B,D正确,C不正确.
9.答案:ABC
解析:根据抽样方法,可知这种抽样方法是简单随机抽样,A正确;易知这5名男生成绩的中位数是90,这5名女生成绩的中位数是93,故B正确;5名男生成绩的平均数为,方差为,5名女生成绩的平均数为
,方差为,故C正确;由于该班男生成绩的平均数与该班女生成绩的平均数不一定是样本的平均数,故D错误.
10.答案:ABD
解析:设丢失的数据为x,则这七个数据的平均数为,众数是3.由题意知,这组数据的平均数与众数的和是中位数的2倍.若,则中位数为3,此时,解得;若,则中位数为x,此时,解得;若,则中位数为5,此时,解得.综上,丢失的数据可能是,4,18.故选ABD.
11.答案:
解析:因为,
所以
,
所以.
12.答案:85
解析:由题意得,该校数学建模兴趣班的平均成绩是(分).
13.答案:48
解析:设这个黄金周该景区游客人数最多的那一天的营业额约为x万元.由,得,则游客人数最多的那一天的营业额约为48万元.
14.答案:(1) 第四组的频率0.3,频率直方图见解析
(2)及格率75%;众数75,中位数约为73.3
解析:(1)因为各组的频率和等于1,故第四组的频率:,
补全频率分布直方图如图所示:
(2)依题意,60及以上的分数所在的第三、四、五、六组频率和为,所以抽样学生成绩的及格率是75%,
众数为最高小矩形底边的中点,是75;
由,知中位数在内,
设中位数为x,则,
解得;所以估计中位数是73.3分.
15.答案:(1)分数在内的频率为0.25,补全频率分布直方图见解析
(2)众数为75分或85分,平均值为70.5分
(3)估计获奖的同学需要的分数至少为88分
解析:(1)分数在内的频率为.
补全频率分布直方图如图所示.
(2)根据频率分布直方图,可估计本次考试成绩的众数为分或分,平均值为分.
(3)根据评奖规则,排名靠前的10%的同学可以获奖,
成绩在的频率为,成绩在的频率为,估计获奖的同学需要的分数至少为(分).
2
1.据某地区气象局发布的气象数据,末来某十天内该地区每天最高温度(单位:℃)分别为:31,29,24,27,26,25,24,26,26,23,则这组数据的第40百分位数为( )
A.27 B.26.5 C.25.5 D.25
2.已知样本数据2,4,6,a的平均数为4,则该样本的标准差是( )
A. B. C.2 D.
3.已知某7个数的平均数为4,方差为2,现加入一个新数据4,此时这8个数的平均数为,方差为,则( )
A. B.
C. D.
4.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是( )
A.中位数 B.平均数 C.方差 D.极差
5.某校进行了一次创新作文大赛,共有100名同学参赛,经过评判,这100名参赛者的得分都在之间,其得分的频率分布直方图如图,则下列结论错误的是( )
A.得分在之间的共有40人
B.从这100名参赛者中随机选取1人,其得分在的概率为0.5
C.估计得分的众数为55
D.这100名参赛者得分的中位数为65
6.某学习小组在一次数学测验中,得100分的有1人,95分的有1人,90分的有2人,85分的有4人,80分和75分的各有1人,则该小组成绩的平均数、众数、中位数分别是( )
A.85,85,85 B.87,85,86 C.87,85,85 D.87,85,90
7.对于数据3,3,2,3,6,3,10,3,6,3,2.有下列说法:
①这组数据的众数是3;
②这组数据的众数与中位数的数值不相等;
③这组数据的中位数与平均数的数值相等;
④这组数据的平均数与众数的数值相等.
其中正确的个数是( )
A.1 B.2 C.3 D.4
8. (多选)中华人民共和国第十四届全国运动会于2021年9月15日在陕西西安开幕.某射击运动员为了在全运会上取得优异成绩,积极训练备战,在某次训练中,该运动员连续射击10次的成绩(单位:环)依次为7,8,8,,6,10,7,9,8,9,因记录员工作失误,有一个数被污染了,但记录员记得这组数据的平均数为8.在去掉其中的一个最高成绩和一个最低成绩后,以下结论正确的是( )
A.众数不变 B.中位数不变 C.极差不变 D.平均数不变
9. (多选)某班有50名学生,其中男生30名,随机询问了该班5名男生和5名女生在某次数学测验中的成绩.5名男生的成绩分别为86,94,88,92,90,5名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( )
A.这种抽样方法是简单随机抽样 B.这5名男生成绩的中位数小于这5名女生成绩的中位数 C.这5名男生成绩的方差大于这5名女生成绩的方差 D.该班男生成绩的平均数小于该班女生成绩的平均数
10. (多选)已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11,若这组数据的平均数与众数的和是中位数的2倍,则丢失的数据可能是( )
A. B.4 C.12 D.18
11.从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为_________.
分数 5 4 3 2 1
人数 20 10 30 30 10
12.某高校有甲、乙两个数学建模兴趣班.其中甲班有40人,乙班有50人.现分析两个班的一次考试成绩,算得甲班的平均成绩是90分,乙班的平均成绩是81分,则该校数学建模兴趣班的平均成绩是________________分.
13.去年,相关部门对某城市“五朵金花”之一的某景区在“十一”黄金周中每天的游客人数作了统计,其频率分布如下表所示:
时间 10月1日 10月2日 10月3日 10月4日 10月5日 10月6日 10月7日
频率 0.05 0.08 0.09 0.13 0.30 0.15 0.20
已知10月1日这天该景区的营业额约为8万元,假定这七天每天游客人均消费相同,则这个黄金周该景区游客数量最多的那一天的营业额约为____________万元.
14.某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图.
(2)估计这次考试的及格率(60分及以上为及格),众数和中位数.(保留整数)
15.为了解某市参加2018年全国高中数学联赛的学生的考试成绩,现从中选取60名同学,将其成绩(百分制,均为正数)分成,,,,,六组后,得到部分频率分布直方图(如图),回答下列问题.
(1)求分数在内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,估计本次考试成绩的众数和平均值;
(3)根据评奖规则,排名靠前的10%的同学可以获奖,请你估计获奖的同学至少需要多少分?
答案以及解析
1.答案:C
解析:第一步:按从小到大排列原始数据先将这些数据按照从小到大进行排序,分别为23,24,24,25,26,26,26,27,29,31,
第二步:计算
计算得,
第三步:得结果
因此该组数据的第40百分位数为.
2.答案:B
解析:因为2,4,6,a的平均数为4,所以,得,所以该样本的标准差,故选B.
3.答案:A
解析:某7 个数的平均数为4,方差为2,则这8个数的平均数为,方差为. 故选:A.
4.答案:A
解析:设9位评委评分按从小到大排列为.
则①原始中位数为,去掉最低分,最高分,后剩余,
中位数仍为,A正确.
②原始平均数,后来平均数
平均数受极端值影响较大,与不一定相同,B不正确
③
由②易知,C不正确.
④原极差,后来极差显然极差变小,D不正确.
5.答案:D
解析:根据频率和为1,计算,解得,得分在的频率是0.40,估计得分在的有(人),A正确;
得分在的频率为0.5,可得这100名参赛者中随机选取一人,得分在的概率为0.5,B正确;
根据频率分布直方图知,最高的小矩形对应的底边中点为,即估计得分众数为55,C正确;
中位数的估计值为,解得,故D错,故选D.
6.答案:C
解析:依题意,将该小组所有数学成绩从小到大列出:75,80,85,85,85,85,90,90,95,100,观察知众数和中位数均为85,计算得平均数为87.
7.答案:A
解析:在这11个数据中,数据3出现了6次,频率最高,故众数是3,①正确;将这11个数据按从小到大排列得2,2,3,3,3,3,3,3,6,6,10,最中间的数据是3,故中位数是3,②错误;这组数据的平均数,故③④错误.故选A.
8.答案:ABD
解析:设被污染的数为a,由这组数据的平均数,解得.这10个数据中8出现了4次,出现的次数最多,所以众数是8.将这10个数据按从小到大的顺序排列,为6,7,7,8,8,8,8,9,9,10,中位数应是第5和第6个数的平均数,即.这组数据中最大的为10,最小的为6,故极差为.去掉其中的一个最大数10和一个最小数6后的8个数据中,众数仍为8,中位数还是8,平均数为8,极差为,所以A,B,D正确,C不正确.
9.答案:ABC
解析:根据抽样方法,可知这种抽样方法是简单随机抽样,A正确;易知这5名男生成绩的中位数是90,这5名女生成绩的中位数是93,故B正确;5名男生成绩的平均数为,方差为,5名女生成绩的平均数为
,方差为,故C正确;由于该班男生成绩的平均数与该班女生成绩的平均数不一定是样本的平均数,故D错误.
10.答案:ABD
解析:设丢失的数据为x,则这七个数据的平均数为,众数是3.由题意知,这组数据的平均数与众数的和是中位数的2倍.若,则中位数为3,此时,解得;若,则中位数为x,此时,解得;若,则中位数为5,此时,解得.综上,丢失的数据可能是,4,18.故选ABD.
11.答案:
解析:因为,
所以
,
所以.
12.答案:85
解析:由题意得,该校数学建模兴趣班的平均成绩是(分).
13.答案:48
解析:设这个黄金周该景区游客人数最多的那一天的营业额约为x万元.由,得,则游客人数最多的那一天的营业额约为48万元.
14.答案:(1) 第四组的频率0.3,频率直方图见解析
(2)及格率75%;众数75,中位数约为73.3
解析:(1)因为各组的频率和等于1,故第四组的频率:,
补全频率分布直方图如图所示:
(2)依题意,60及以上的分数所在的第三、四、五、六组频率和为,所以抽样学生成绩的及格率是75%,
众数为最高小矩形底边的中点,是75;
由,知中位数在内,
设中位数为x,则,
解得;所以估计中位数是73.3分.
15.答案:(1)分数在内的频率为0.25,补全频率分布直方图见解析
(2)众数为75分或85分,平均值为70.5分
(3)估计获奖的同学需要的分数至少为88分
解析:(1)分数在内的频率为.
补全频率分布直方图如图所示.
(2)根据频率分布直方图,可估计本次考试成绩的众数为分或分,平均值为分.
(3)根据评奖规则,排名靠前的10%的同学可以获奖,
成绩在的频率为,成绩在的频率为,估计获奖的同学需要的分数至少为(分).
2
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
