5.1.3 同位角、内错角、同旁内角 课件 (共27张PPT)
文档属性
| 名称 | 5.1.3 同位角、内错角、同旁内角 课件 (共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-07 17:45:35 | ||
图片预览





文档简介
(共27张PPT)
人教七下数学同步精品课件
人教版七年级下册
交流预习
2023春人教版七(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第五章 相交线与平行线
5.1 相交线
5.1.3 同位角、内错角、同旁内角
核心素养目标:
在截线的同旁找同位角和同旁内角,在截线的两旁找内错角.要结合图形,熟记同位角、内错角、同旁内角的位置特点,比较它们的区别与联系.
在复杂的图形中识别同位角、内错角、同旁内角时,应当沿着角的边将图形补全,或者把多余的线暂时略去,找到三线八角的基本图形,进而确定这两个角的位置关系.
准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.
了解两条直线被第三条直线所截,构成八个角(简称“三线八角”),其中同位角4对,内错角2对,同旁内角2对.
问题: 两条直线AB和CD相交,任意两个角都有什么关系?
3
2
2
1
3
4
1
4
C
D
B
A
1
3
4
2
复习引入:
四对邻补角:
∠1和∠2;
∠2和∠3;
∠3和∠4;
∠4和∠1.
4
2
1
3
两对对顶角:
∠1和∠3;
∠2和∠4.
6
7
5
8
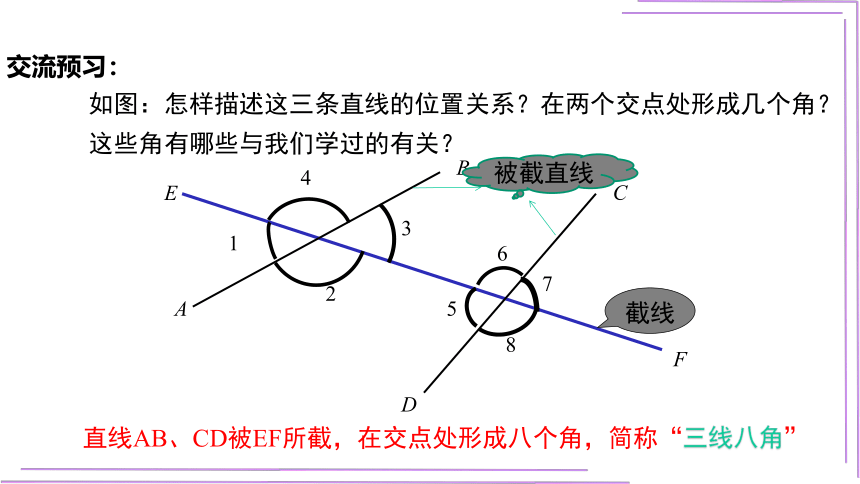
直线AB、CD被EF所截,在交点处形成八个角,简称“三线八角”
如图:怎样描述这三条直线的位置关系?在两个交点处形成几个角?这些角有哪些与我们学过的有关?
B
A
F
E
C
D
4
3
1
2
交流预习:
截线
被截直线
5
1
7
8
5
4
1
3
2
6
2
6
7
3
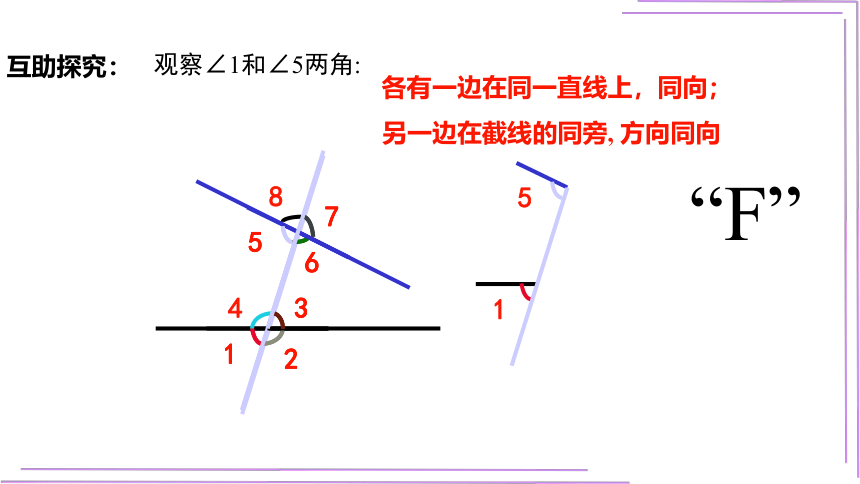
观察∠1和∠5两角:
“F”
互助探究:
各有一边在同一直线上,同向;
另一边在截线的同旁, 方向同向
5
1
5
1
7
8
5
4
1
3
2
6
2
6
7
3
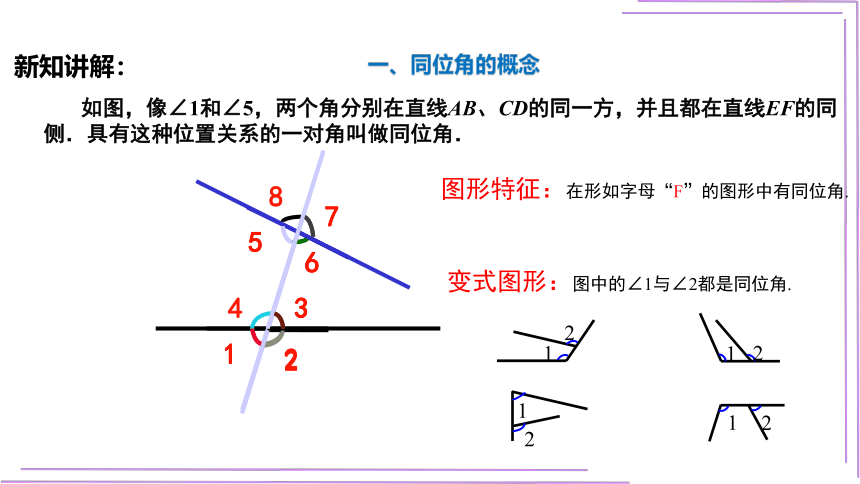
一、同位角的概念
新知讲解:
如图,像∠1和∠5,两个角分别在直线AB、CD的同一方,并且都在直线EF的同侧.具有这种位置关系的一对角叫做同位角.
变式图形:图中的∠1与∠2都是同位角.
图形特征:在形如字母“F”的图形中有同位角.
1
2
1
2
1
2
1
2
5
1
7
8
5
4
1
3
2
6
2
6
7
3
8
4
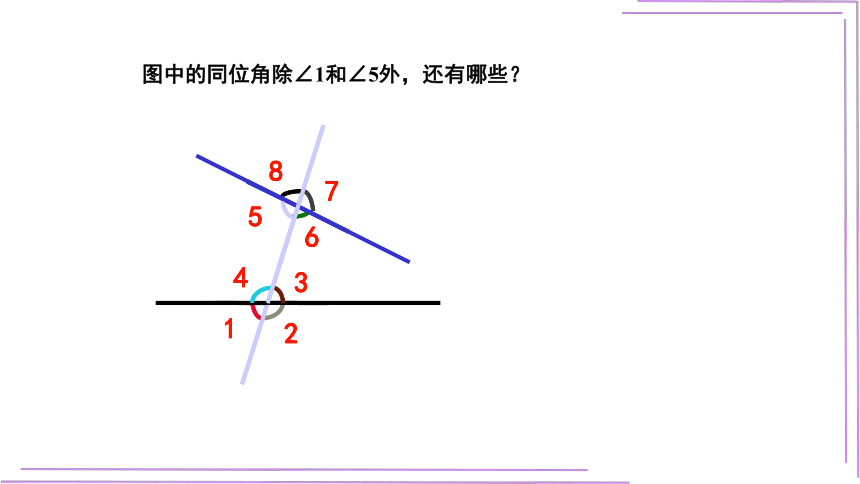
图中的同位角除∠1和∠5外,还有哪些?
互助探究:
观察∠3和∠5两角:
5
1
7
8
5
4
1
3
2
6
2
6
7
3
5
3
各有一边在同一直线上,反向;
5
3
另一边在截线的两侧, 方向相反
“Z”
5
1
7
8
5
4
1
3
2
6
2
6
7
3
二、内错角的概念
新知讲解:
如图,像∠3和∠5,两个角都在直线AB、CD之间,并且分别在直线EF两侧.具有这种位置关系的一对角叫做内错角.
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
7
8
5
4
1
3
2
6
5
3
4
6
图中的内错角除∠3和∠5外,还有哪些?
5
1
7
8
5
4
1
3
2
6
2
6
7
3
另一边在截线的同旁, 方向相同
3
6
互助探究:
观察∠3和∠6两角:
各有一边在同一直线上,反向
“U”
5
1
7
8
5
4
1
3
2
6
2
6
7
3
三、同旁内角的概念
新知讲解:
如图,像∠3和∠6,两个角都在直线AB、CD之间,并且都在直线EF的同一旁.具有这种位置关系的一对角叫做同旁内角.
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
7
8
5
4
1
3
2
6
5
4
3
6
图中的同旁内角除∠3和∠6外,还有哪些?
形如字母“U”
在两条被截直线同旁,在截线同侧
同旁内角
形如字母“Z”
(或反置)
在两条被截直线之内,在截线两侧(交错)
内错角
形如字母“F”
(或倒置)
在两条被截直线同旁,在截线同侧
同位角
图形结构特征
位 置 特 征
角的名称
总结归纳:
例1 如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
4
3
2
1
F
E
D
C
B
A
解:(1)∠1与∠2是内错角,∠1和∠3同旁角,∠1和∠4是同旁内角.
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与
∠3互补吗? 为什么?
解:(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,那∠1=∠2.因为∠3和∠4互补,即∠4+∠3=180°,又因为∠1=∠4,所以∠4+∠3=180°,即∠1与∠3互补.
例题精讲:
教材7页练习1(1).分别指出下列图中的同位角、内错角、同旁内角.
同位角:∠2与∠6,∠4与∠8,∠3与∠7,∠1与∠5
内错角:∠3与∠6,∠4与∠5
同旁内角:∠3与∠5,∠4与∠6
跟踪练习:
同位角:∠1与∠3,∠2与∠4.
内错角:无.
同旁内角:∠2与 ∠3.
教材7页练习1(2)分别指出下列图中的同位角、内错角、同旁内角.
跟踪练习:
教材7页练习2. 如图,∠B 与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C 进行同样的讨论.
跟踪练习:
解:∠B 与∠DAB 是内错角,与∠BAE 是同旁内角,它们都是由 DE 与 BC 被 AB 所截形成的,还与∠BAC 是同旁内角,它们是由 AC、BC被BA 所截形成的.∠C 与∠EAC 是内错角,与∠DAC 是同旁内角,它们都是由 DE 与 BC 被 AC 所截形成的.还与∠BAC 是同旁内角,它们是由 AB、BC 被 AC 所截形成的.
三线八角
同位角 “F”型
同旁内角 “U”型
判断方法
(描图法)
①把两个角在图中描画出来;
②找到两个角的公共直线;
③观察所描的角,判断所属“字母”类型,
同 位角为“F”型,内错角为“Z”型,同
旁内角为“U”型,注意图形的变式(旋
转、对称)也是符合的.
内错角 “Z”型
课堂小结:
1.如图,∠DAB和∠ABC的位置关系是 ( )
A.同位角 B.同旁内角
C.内错角 D.以上结论都不对
2.如图,∠1和∠2不能构成同位角的图形是( )
C
D
A
D
B
C
E
课堂检测:
(1)如图1,若ED,BF被AB所截,则∠1与____是同位角.
3.看图填空:
∠2
(2)如图2,若ED,BC被AF所截,则∠3与___ 是内错角.
∠4
图1
图2
课堂检测:
(3)如图3,∠1与∠3是AB和AF被_____所截构成的 角;
DE
内错
(4)如图4,∠2与∠4是 和 被BC所截构成的____角.
AB
AF
同位
图3
图4
课堂检测:
课后作业:
必做题:教材7页练习
选做题:习题5.1第11题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七下数学同步精品课件
人教版七年级下册
交流预习
2023春人教版七(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第五章 相交线与平行线
5.1 相交线
5.1.3 同位角、内错角、同旁内角
核心素养目标:
在截线的同旁找同位角和同旁内角,在截线的两旁找内错角.要结合图形,熟记同位角、内错角、同旁内角的位置特点,比较它们的区别与联系.
在复杂的图形中识别同位角、内错角、同旁内角时,应当沿着角的边将图形补全,或者把多余的线暂时略去,找到三线八角的基本图形,进而确定这两个角的位置关系.
准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.
了解两条直线被第三条直线所截,构成八个角(简称“三线八角”),其中同位角4对,内错角2对,同旁内角2对.
问题: 两条直线AB和CD相交,任意两个角都有什么关系?
3
2
2
1
3
4
1
4
C
D
B
A
1
3
4
2
复习引入:
四对邻补角:
∠1和∠2;
∠2和∠3;
∠3和∠4;
∠4和∠1.
4
2
1
3
两对对顶角:
∠1和∠3;
∠2和∠4.
6
7
5
8
直线AB、CD被EF所截,在交点处形成八个角,简称“三线八角”
如图:怎样描述这三条直线的位置关系?在两个交点处形成几个角?这些角有哪些与我们学过的有关?
B
A
F
E
C
D
4
3
1
2
交流预习:
截线
被截直线
5
1
7
8
5
4
1
3
2
6
2
6
7
3
观察∠1和∠5两角:
“F”
互助探究:
各有一边在同一直线上,同向;
另一边在截线的同旁, 方向同向
5
1
5
1
7
8
5
4
1
3
2
6
2
6
7
3
一、同位角的概念
新知讲解:
如图,像∠1和∠5,两个角分别在直线AB、CD的同一方,并且都在直线EF的同侧.具有这种位置关系的一对角叫做同位角.
变式图形:图中的∠1与∠2都是同位角.
图形特征:在形如字母“F”的图形中有同位角.
1
2
1
2
1
2
1
2
5
1
7
8
5
4
1
3
2
6
2
6
7
3
8
4
图中的同位角除∠1和∠5外,还有哪些?
互助探究:
观察∠3和∠5两角:
5
1
7
8
5
4
1
3
2
6
2
6
7
3
5
3
各有一边在同一直线上,反向;
5
3
另一边在截线的两侧, 方向相反
“Z”
5
1
7
8
5
4
1
3
2
6
2
6
7
3
二、内错角的概念
新知讲解:
如图,像∠3和∠5,两个角都在直线AB、CD之间,并且分别在直线EF两侧.具有这种位置关系的一对角叫做内错角.
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
7
8
5
4
1
3
2
6
5
3
4
6
图中的内错角除∠3和∠5外,还有哪些?
5
1
7
8
5
4
1
3
2
6
2
6
7
3
另一边在截线的同旁, 方向相同
3
6
互助探究:
观察∠3和∠6两角:
各有一边在同一直线上,反向
“U”
5
1
7
8
5
4
1
3
2
6
2
6
7
3
三、同旁内角的概念
新知讲解:
如图,像∠3和∠6,两个角都在直线AB、CD之间,并且都在直线EF的同一旁.具有这种位置关系的一对角叫做同旁内角.
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
7
8
5
4
1
3
2
6
5
4
3
6
图中的同旁内角除∠3和∠6外,还有哪些?
形如字母“U”
在两条被截直线同旁,在截线同侧
同旁内角
形如字母“Z”
(或反置)
在两条被截直线之内,在截线两侧(交错)
内错角
形如字母“F”
(或倒置)
在两条被截直线同旁,在截线同侧
同位角
图形结构特征
位 置 特 征
角的名称
总结归纳:
例1 如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
4
3
2
1
F
E
D
C
B
A
解:(1)∠1与∠2是内错角,∠1和∠3同旁角,∠1和∠4是同旁内角.
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与
∠3互补吗? 为什么?
解:(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,那∠1=∠2.因为∠3和∠4互补,即∠4+∠3=180°,又因为∠1=∠4,所以∠4+∠3=180°,即∠1与∠3互补.
例题精讲:
教材7页练习1(1).分别指出下列图中的同位角、内错角、同旁内角.
同位角:∠2与∠6,∠4与∠8,∠3与∠7,∠1与∠5
内错角:∠3与∠6,∠4与∠5
同旁内角:∠3与∠5,∠4与∠6
跟踪练习:
同位角:∠1与∠3,∠2与∠4.
内错角:无.
同旁内角:∠2与 ∠3.
教材7页练习1(2)分别指出下列图中的同位角、内错角、同旁内角.
跟踪练习:
教材7页练习2. 如图,∠B 与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C 进行同样的讨论.
跟踪练习:
解:∠B 与∠DAB 是内错角,与∠BAE 是同旁内角,它们都是由 DE 与 BC 被 AB 所截形成的,还与∠BAC 是同旁内角,它们是由 AC、BC被BA 所截形成的.∠C 与∠EAC 是内错角,与∠DAC 是同旁内角,它们都是由 DE 与 BC 被 AC 所截形成的.还与∠BAC 是同旁内角,它们是由 AB、BC 被 AC 所截形成的.
三线八角
同位角 “F”型
同旁内角 “U”型
判断方法
(描图法)
①把两个角在图中描画出来;
②找到两个角的公共直线;
③观察所描的角,判断所属“字母”类型,
同 位角为“F”型,内错角为“Z”型,同
旁内角为“U”型,注意图形的变式(旋
转、对称)也是符合的.
内错角 “Z”型
课堂小结:
1.如图,∠DAB和∠ABC的位置关系是 ( )
A.同位角 B.同旁内角
C.内错角 D.以上结论都不对
2.如图,∠1和∠2不能构成同位角的图形是( )
C
D
A
D
B
C
E
课堂检测:
(1)如图1,若ED,BF被AB所截,则∠1与____是同位角.
3.看图填空:
∠2
(2)如图2,若ED,BC被AF所截,则∠3与___ 是内错角.
∠4
图1
图2
课堂检测:
(3)如图3,∠1与∠3是AB和AF被_____所截构成的 角;
DE
内错
(4)如图4,∠2与∠4是 和 被BC所截构成的____角.
AB
AF
同位
图3
图4
课堂检测:
课后作业:
必做题:教材7页练习
选做题:习题5.1第11题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
