5.1.1 相交线同步导学案【2023春人教版七下数学精品备课】
文档属性
| 名称 | 5.1.1 相交线同步导学案【2023春人教版七下数学精品备课】 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
5.1.1相交线导学案
学段 初中 年级 七年级 学科 数 学
单元 第5单元 课题 5.1相交线 课型 新授
课标 依据 理解对顶角、余角、补角等概念,探索并掌握对顶角相等、同角(等角)的余角相等,同角(等角)的补角相等的性质。
核心素养目标 1.理解对顶角和邻补角的概念,能在图形中辨认; 2.掌握对顶角相等的性质和它的推证过程; 3.通过在图形中辨认对顶角和邻补角,培养学生的识图能力.
教学 重点 邻补角与对顶角的概念.
教学 难点 对顶角性质与应用
导学 环节 课堂 流程 时间 任务驱动 问题导学 学法 指导 知识 链接
呈现 目标 呈现本节课的学习目标,并让学生诵读
导入新课 温故 知新 2 阅读课本P1图片及文字,了解本章要学习哪些知识 应学会哪些数学方法 培养哪些良好习惯 , 角的表示方法 角的计算 互补的理解
图片导入 1 观察图片,说一说直线与直线的位置关系.直线与直线相交于一点,并形成了四个角. 观察
互 助 探 究 动手实践 4 1.准备一张纸片和一把剪刀,用剪刀将纸片剪开,观察剪纸过程,握紧把手时, 随着两个把手之间的角逐渐变小,剪刀两刀刃之间的角引发了什么变化 . 如果改变用力方向,将两个把手之间的角逐渐变大,剪刀两刀刃之间的角又发生什么了变化 . 2.如果把剪刀的构造看作是两条相交的直线, 剪纸过程就关系到两条相交直线所成的角的问题, 阅读课本P2内容,探讨两条相交线所成的角有哪些 各有什么特征 动手操作
提出猜想 验证猜想 13 1.画直线AB、CD相交于点O,并说出图中4个角,两两相配共能组成几对角 各对角的位置关系如何 根据不同的位置怎么将它们分类 例如: (1)∠AOC和∠BOC有一条公共边OC,它们的另一边互为 ,称这两个角互为 。用量角器量一量这两个角的度数,会发现它们的数量关系是 (2)∠AOC和∠BOD (有或没有)公共边,但∠AOC的两边分别是∠BOD两边的 ,称这两个角互为 。用量角器量一量这两个角的度数,会发现它们的数量关系是 。 3.用语言概括邻补角、对顶角概念. 的两个角叫邻补角。 的两个角叫对顶角。 4.探究对顶角性质. 在图1中,∠AOC的邻补角有两个,是 和 ,根据“同角的补角相等”,可以得出 = ,而这两个角又是对顶角,由此得到对顶角性质:对顶角相等. 注意:对顶角概念与对顶角性质不能混淆,对顶角的概念是确定两角的位置关系,对顶角性质是确定为对顶角的两角的数量关系. 你能利用“对顶角相等”这条性质解释剪刀剪纸过程中所看到的现象吗? 自 学 探 究 小 组 合 作
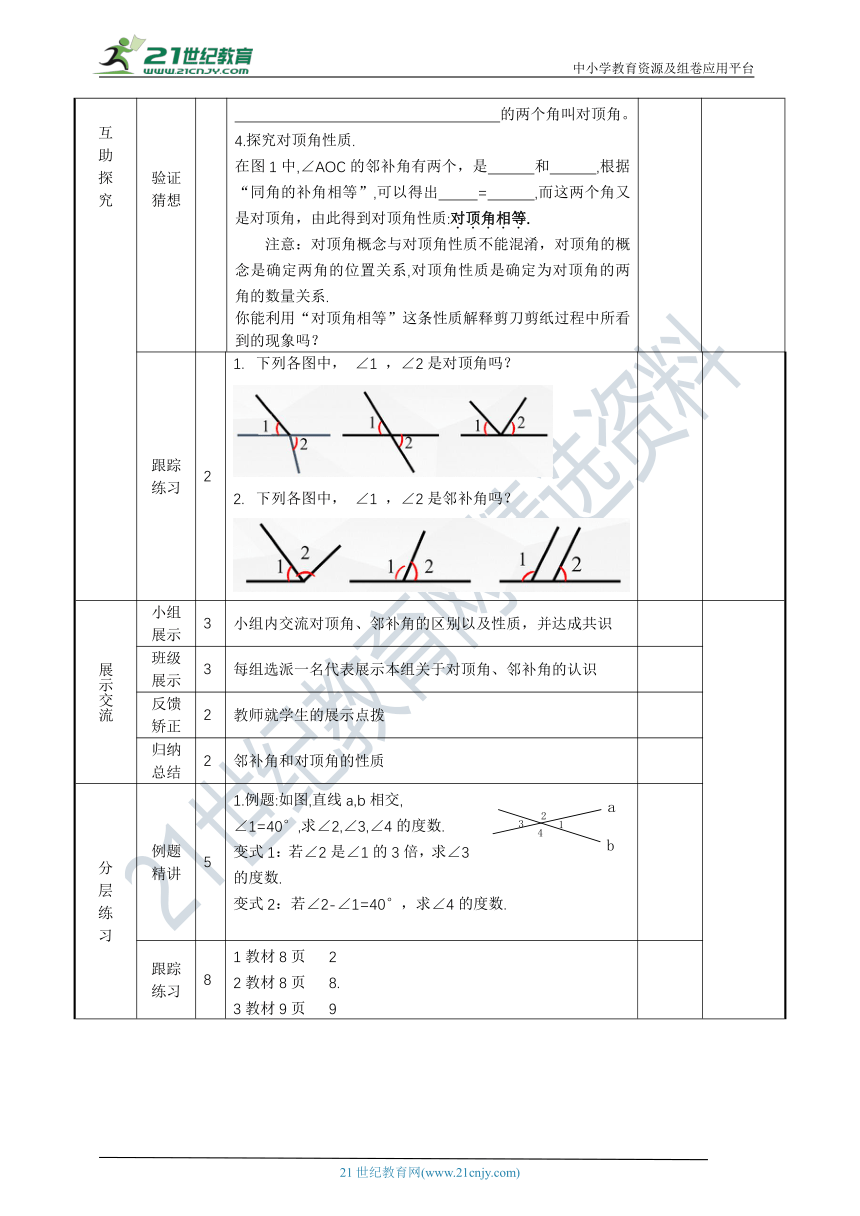
跟踪练习 2 下列各图中, ∠1 ,∠2是对顶角吗? 下列各图中, ∠1 ,∠2是邻补角吗?
展示交流 小组 展示 3 小组内交流对顶角、邻补角的区别以及性质,并达成共识
班级 展示 3 每组选派一名代表展示本组关于对顶角、邻补角的认识
反馈 矫正 2 教师就学生的展示点拨
归纳总结 2 邻补角和对顶角的性质
分 层 练 习 例题精讲 5 1.例题:如图,直线a,b相交, ∠1=40°,求∠2,∠3,∠4的度数. 变式1:若∠2是∠1的3倍,求∠3的度数. 变式2:若∠2-∠1=40°,求∠4的度数.
跟踪练习 8 1教材8页 2 2教材8页 8. 3教材9页 9
总 结 升 华
课 后 反 思 成功之处:本节课是在七年级上册学过线、角的有关知识的基础上,进一步研究两直线位置关系的第一课时.对顶角是几何求解、证明中的一个基本图形,其中对顶角相等也是证明中常用的结论,以此实现角之间的相互转化.内容相对简单,但又非常重要。对顶角的概念出来后,立即找到生活原型,以加强认识,联系生活.在辨别给出图形是否为对顶角的一组题目中,果然如课前所料,学生的几何语言运用不够熟练、严谨,我耐心地纠正,原因是几何开始一定要让学生重视几何语言的表述,养成学习几何的好习惯.在这个题目中我始终让学生对照定义辨别,加强认识.探究对顶角相等这个性质是本课时的重难点,所以我的设计是先画图量角,让学生有一个感性认识,同时让学生认识到度量是有误差的,所以叫学生记下读数,提出可不可以根据一个角的度数,计算出其对顶角的度数这样一个问题,其实这个问题设计是承上启下的,因为在证明时我听到他们说出“和刚才计算一样”的话.练习题的设置一来是巩固,二来时让学生体会转化思想. 不足之处:本节课通过对比教学,学生对概念的理解及简单的一些推理说明基本能掌握,但可能是课堂上没有照顾到所有的学生导致部分学习有困难的孩子对推理说明类似的题目在解题过程中出现乱、繁等现象(个别学生甚至无法下手).课后要根据实际情况及时进行补差补缺,争取不让一个孩子掉队.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.1.1相交线导学案
学段 初中 年级 七年级 学科 数 学
单元 第5单元 课题 5.1相交线 课型 新授
课标 依据 理解对顶角、余角、补角等概念,探索并掌握对顶角相等、同角(等角)的余角相等,同角(等角)的补角相等的性质。
核心素养目标 1.理解对顶角和邻补角的概念,能在图形中辨认; 2.掌握对顶角相等的性质和它的推证过程; 3.通过在图形中辨认对顶角和邻补角,培养学生的识图能力.
教学 重点 邻补角与对顶角的概念.
教学 难点 对顶角性质与应用
导学 环节 课堂 流程 时间 任务驱动 问题导学 学法 指导 知识 链接
呈现 目标 呈现本节课的学习目标,并让学生诵读
导入新课 温故 知新 2 阅读课本P1图片及文字,了解本章要学习哪些知识 应学会哪些数学方法 培养哪些良好习惯 , 角的表示方法 角的计算 互补的理解
图片导入 1 观察图片,说一说直线与直线的位置关系.直线与直线相交于一点,并形成了四个角. 观察
互 助 探 究 动手实践 4 1.准备一张纸片和一把剪刀,用剪刀将纸片剪开,观察剪纸过程,握紧把手时, 随着两个把手之间的角逐渐变小,剪刀两刀刃之间的角引发了什么变化 . 如果改变用力方向,将两个把手之间的角逐渐变大,剪刀两刀刃之间的角又发生什么了变化 . 2.如果把剪刀的构造看作是两条相交的直线, 剪纸过程就关系到两条相交直线所成的角的问题, 阅读课本P2内容,探讨两条相交线所成的角有哪些 各有什么特征 动手操作
提出猜想 验证猜想 13 1.画直线AB、CD相交于点O,并说出图中4个角,两两相配共能组成几对角 各对角的位置关系如何 根据不同的位置怎么将它们分类 例如: (1)∠AOC和∠BOC有一条公共边OC,它们的另一边互为 ,称这两个角互为 。用量角器量一量这两个角的度数,会发现它们的数量关系是 (2)∠AOC和∠BOD (有或没有)公共边,但∠AOC的两边分别是∠BOD两边的 ,称这两个角互为 。用量角器量一量这两个角的度数,会发现它们的数量关系是 。 3.用语言概括邻补角、对顶角概念. 的两个角叫邻补角。 的两个角叫对顶角。 4.探究对顶角性质. 在图1中,∠AOC的邻补角有两个,是 和 ,根据“同角的补角相等”,可以得出 = ,而这两个角又是对顶角,由此得到对顶角性质:对顶角相等. 注意:对顶角概念与对顶角性质不能混淆,对顶角的概念是确定两角的位置关系,对顶角性质是确定为对顶角的两角的数量关系. 你能利用“对顶角相等”这条性质解释剪刀剪纸过程中所看到的现象吗? 自 学 探 究 小 组 合 作
跟踪练习 2 下列各图中, ∠1 ,∠2是对顶角吗? 下列各图中, ∠1 ,∠2是邻补角吗?
展示交流 小组 展示 3 小组内交流对顶角、邻补角的区别以及性质,并达成共识
班级 展示 3 每组选派一名代表展示本组关于对顶角、邻补角的认识
反馈 矫正 2 教师就学生的展示点拨
归纳总结 2 邻补角和对顶角的性质
分 层 练 习 例题精讲 5 1.例题:如图,直线a,b相交, ∠1=40°,求∠2,∠3,∠4的度数. 变式1:若∠2是∠1的3倍,求∠3的度数. 变式2:若∠2-∠1=40°,求∠4的度数.
跟踪练习 8 1教材8页 2 2教材8页 8. 3教材9页 9
总 结 升 华
课 后 反 思 成功之处:本节课是在七年级上册学过线、角的有关知识的基础上,进一步研究两直线位置关系的第一课时.对顶角是几何求解、证明中的一个基本图形,其中对顶角相等也是证明中常用的结论,以此实现角之间的相互转化.内容相对简单,但又非常重要。对顶角的概念出来后,立即找到生活原型,以加强认识,联系生活.在辨别给出图形是否为对顶角的一组题目中,果然如课前所料,学生的几何语言运用不够熟练、严谨,我耐心地纠正,原因是几何开始一定要让学生重视几何语言的表述,养成学习几何的好习惯.在这个题目中我始终让学生对照定义辨别,加强认识.探究对顶角相等这个性质是本课时的重难点,所以我的设计是先画图量角,让学生有一个感性认识,同时让学生认识到度量是有误差的,所以叫学生记下读数,提出可不可以根据一个角的度数,计算出其对顶角的度数这样一个问题,其实这个问题设计是承上启下的,因为在证明时我听到他们说出“和刚才计算一样”的话.练习题的设置一来是巩固,二来时让学生体会转化思想. 不足之处:本节课通过对比教学,学生对概念的理解及简单的一些推理说明基本能掌握,但可能是课堂上没有照顾到所有的学生导致部分学习有困难的孩子对推理说明类似的题目在解题过程中出现乱、繁等现象(个别学生甚至无法下手).课后要根据实际情况及时进行补差补缺,争取不让一个孩子掉队.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
