1.2.2 运动的合成与分解 (第二课时)(课件)(19张PPT)高一物理同步精品课堂(教科版2019 必修第二册)
文档属性
| 名称 | 1.2.2 运动的合成与分解 (第二课时)(课件)(19张PPT)高一物理同步精品课堂(教科版2019 必修第二册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-07 20:25:21 | ||
图片预览





文档简介
第2节 运动的合成与分解
1.2.2
小船过河问题
课堂导入
一、小船过河问题
1.模型特点
两个分运动和合运动都是匀速直线运动,其中一个分运动的速度大小、方向都不变,另一分运动的速度大小不变, 研究其速度方向不同时对合运动的影响,这样的运动系统可看做小船渡河模型。
2.模型分析
(1)船的实际运动是水流的运动和船相对静水的运动的合运动。
(2)三种速度:v1(船在静水中的速度)、v2(水流速度)、v(船的实际速度)。
一、小船过河问题
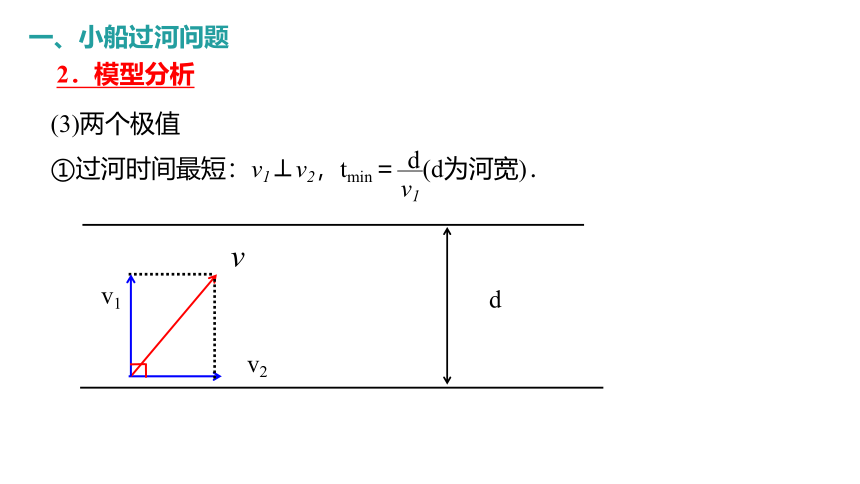
(3)两个极值
①过河时间最短:v1⊥v2,tmin=—(d为河宽).
d
v1
v1
d
v2
2.模型分析
一、小船过河问题
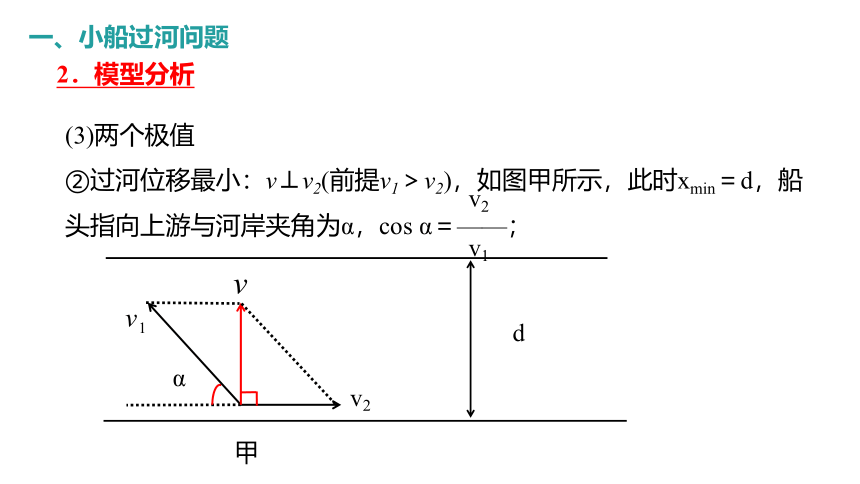
(3)两个极值
②过河位移最小:v⊥v2(前提v1>v2),如图甲所示,此时xmin=d,船头指向上游与河岸夹角为α,cos α=——;
v2
v1
d
α
甲
v2
2.模型分析
θ
θ
结论:当v船< v水时,最短航程不等于河宽d。
船头指向与上游河岸成θ:
一、小船过河问题
2.模型分析
(3)两个极值
过河位移最小:v1⊥v(前提v1<v2),如图乙所示。过河最小位移为
xmin=_____ =____ d
d
α
d
sinα
v2
v1
一、小船过河问题
【对点训练1】小船要渡过200 m宽的河,水流速度为2 m/s,船在静水中的速度为4 m/s,求:
(1)若小船的船头始终正对对岸,它将在何时、何处到达对岸?
(2)要使小船到达正对岸,应如何航行?历时多久?
(3)小船渡河的最短时间为多少?
(4)若水流速度是5 m/s,船在静水中的速度是3 m/s,则怎样渡河才能使船驶向下游的距离最小?最小距离是多少?(结果取整数)
解析:
(1)小船渡河过程参与了两个分运动,即船随水流的运动和船在静水中的运动.因为分运动之间具有独立性和等时性,故小船渡河时间等于它垂直河岸方向上的分运动的时间,即
t⊥= ?????????船???=2004 s=50 s.
小船沿水流方向的位移s水=v水t⊥=2×50 m=100 m
即船将在正对岸下游100 m处靠岸.
?
一、小船过河问题
(2)要使小船到达正对岸,即合速度v应垂直于河岸,如图所示,则cos θ=????水????船 =24=12,θ=60°,即船头与上游河岸的夹角为60°.
渡河时间t′=????????=2004sin?60°s=10033 s.
?
(3)考虑一般情况,设船头与上游河岸的夹角为α.如图所示.船的渡河时间取决于船垂直于河岸方向上的分速度v⊥=v船sin α,故小船渡河时间为t=????????船sin????,当α=90°,即船头与河岸垂直时,渡河时间最短,最短时间为tmin=50 s.
?
一、小船过河问题
(4)因为v′船?
二、关联速度问题
绳、杆关联问题是指物拉绳(杆)或绳(杆)拉物问题.高中阶段研究的绳都是不可伸长的,杆都是不可伸长和不可压缩的,即绳或杆的长度不会改变,所以解题的原则是:把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量,根据沿绳(杆)方向的分速度大小相等求解.
二、关联速度问题
【对点训练2】 质量为m的物体P置于倾
角为θ1的固定光滑斜面上,轻细绳跨过
理想定滑轮分别连接着P与小车,P与滑轮间的细绳平行于斜面,小车以速率v水平向右做匀速直线运动。如图,当小车与滑轮间的细绳和水平方向成夹角θ2时,下列判断正确的是( )
A.P的速率为v B.P的速率为vcos θ2
C.绳的拉力等于mgsin θ1 D.绳的拉力小于mgsin θ1
二、关联速度问题
解析:将小车的速度v进行分解,如图所示,则有vP=vcos θ2,故A错误,B正确。小车向右运动,θ2减小,v不变,则vP逐渐增大,说明物体P沿斜面向上做加速运动,由牛顿第二定律有FT-mgsin θ1=ma,可知绳对P的拉力FT>mgsin θ1,故C、D错误。
二、关联速度问题
分析“关联”速度的基本步骤
课堂小结
运动的合成与分解的应用
小船过河
关联速度
课堂练习
1.(小船渡河问题)如图所示,小船过河时,船头偏向上游,与水流方向成α角,船相对于静水的速度为v,其航线恰好垂直于河岸。现水流速度稍有减小,为保持航线不变,且准时到达对岸,下列措施中可行的是( )
A.增大α角,增大v
B.减小α角,减小v
C.减小α角,保持v不变
D.增大α角,保持v不变
解析:当水流速度稍有减小时,为保持航线不变,且准时到达对岸,如题图所示,可知应减小α角,减小v,故B正确,A、C、D错误。
课堂练习
2.(关联速度)图中套在竖直细杆上的环A由跨过定滑轮的不可伸长的轻绳与重物B相连.由于B的质量较大,故在释放B后,A将沿杆上升,当A环上升至与定滑轮的连线处于水平位置时,其上升速度v1≠0,若这时B的速度为v2,则 ( )
A.v2=v1 B.v2>v1
C.v2≠0 D.v2=0
解析:环上升过程的速度v1可分解为两个分速度v∥和v⊥,如图所示,其中v∥为沿绳方向的速度,其大小等于重物B的速度v2;v⊥为绕定滑轮转动的速度.关系式为v2=v1cos θ,θ为v1与v∥间的夹角.当A上升至与定滑轮的连线处于水平位置时,θ=90°,cos θ=0,即此时v2=0,D项正确.
1.2.2
小船过河问题
课堂导入
一、小船过河问题
1.模型特点
两个分运动和合运动都是匀速直线运动,其中一个分运动的速度大小、方向都不变,另一分运动的速度大小不变, 研究其速度方向不同时对合运动的影响,这样的运动系统可看做小船渡河模型。
2.模型分析
(1)船的实际运动是水流的运动和船相对静水的运动的合运动。
(2)三种速度:v1(船在静水中的速度)、v2(水流速度)、v(船的实际速度)。
一、小船过河问题
(3)两个极值
①过河时间最短:v1⊥v2,tmin=—(d为河宽).
d
v1
v1
d
v2
2.模型分析
一、小船过河问题
(3)两个极值
②过河位移最小:v⊥v2(前提v1>v2),如图甲所示,此时xmin=d,船头指向上游与河岸夹角为α,cos α=——;
v2
v1
d
α
甲
v2
2.模型分析
θ
θ
结论:当v船< v水时,最短航程不等于河宽d。
船头指向与上游河岸成θ:
一、小船过河问题
2.模型分析
(3)两个极值
过河位移最小:v1⊥v(前提v1<v2),如图乙所示。过河最小位移为
xmin=_____ =____ d
d
α
d
sinα
v2
v1
一、小船过河问题
【对点训练1】小船要渡过200 m宽的河,水流速度为2 m/s,船在静水中的速度为4 m/s,求:
(1)若小船的船头始终正对对岸,它将在何时、何处到达对岸?
(2)要使小船到达正对岸,应如何航行?历时多久?
(3)小船渡河的最短时间为多少?
(4)若水流速度是5 m/s,船在静水中的速度是3 m/s,则怎样渡河才能使船驶向下游的距离最小?最小距离是多少?(结果取整数)
解析:
(1)小船渡河过程参与了两个分运动,即船随水流的运动和船在静水中的运动.因为分运动之间具有独立性和等时性,故小船渡河时间等于它垂直河岸方向上的分运动的时间,即
t⊥= ?????????船???=2004 s=50 s.
小船沿水流方向的位移s水=v水t⊥=2×50 m=100 m
即船将在正对岸下游100 m处靠岸.
?
一、小船过河问题
(2)要使小船到达正对岸,即合速度v应垂直于河岸,如图所示,则cos θ=????水????船 =24=12,θ=60°,即船头与上游河岸的夹角为60°.
渡河时间t′=????????=2004sin?60°s=10033 s.
?
(3)考虑一般情况,设船头与上游河岸的夹角为α.如图所示.船的渡河时间取决于船垂直于河岸方向上的分速度v⊥=v船sin α,故小船渡河时间为t=????????船sin????,当α=90°,即船头与河岸垂直时,渡河时间最短,最短时间为tmin=50 s.
?
一、小船过河问题
(4)因为v′船
二、关联速度问题
绳、杆关联问题是指物拉绳(杆)或绳(杆)拉物问题.高中阶段研究的绳都是不可伸长的,杆都是不可伸长和不可压缩的,即绳或杆的长度不会改变,所以解题的原则是:把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量,根据沿绳(杆)方向的分速度大小相等求解.
二、关联速度问题
【对点训练2】 质量为m的物体P置于倾
角为θ1的固定光滑斜面上,轻细绳跨过
理想定滑轮分别连接着P与小车,P与滑轮间的细绳平行于斜面,小车以速率v水平向右做匀速直线运动。如图,当小车与滑轮间的细绳和水平方向成夹角θ2时,下列判断正确的是( )
A.P的速率为v B.P的速率为vcos θ2
C.绳的拉力等于mgsin θ1 D.绳的拉力小于mgsin θ1
二、关联速度问题
解析:将小车的速度v进行分解,如图所示,则有vP=vcos θ2,故A错误,B正确。小车向右运动,θ2减小,v不变,则vP逐渐增大,说明物体P沿斜面向上做加速运动,由牛顿第二定律有FT-mgsin θ1=ma,可知绳对P的拉力FT>mgsin θ1,故C、D错误。
二、关联速度问题
分析“关联”速度的基本步骤
课堂小结
运动的合成与分解的应用
小船过河
关联速度
课堂练习
1.(小船渡河问题)如图所示,小船过河时,船头偏向上游,与水流方向成α角,船相对于静水的速度为v,其航线恰好垂直于河岸。现水流速度稍有减小,为保持航线不变,且准时到达对岸,下列措施中可行的是( )
A.增大α角,增大v
B.减小α角,减小v
C.减小α角,保持v不变
D.增大α角,保持v不变
解析:当水流速度稍有减小时,为保持航线不变,且准时到达对岸,如题图所示,可知应减小α角,减小v,故B正确,A、C、D错误。
课堂练习
2.(关联速度)图中套在竖直细杆上的环A由跨过定滑轮的不可伸长的轻绳与重物B相连.由于B的质量较大,故在释放B后,A将沿杆上升,当A环上升至与定滑轮的连线处于水平位置时,其上升速度v1≠0,若这时B的速度为v2,则 ( )
A.v2=v1 B.v2>v1
C.v2≠0 D.v2=0
解析:环上升过程的速度v1可分解为两个分速度v∥和v⊥,如图所示,其中v∥为沿绳方向的速度,其大小等于重物B的速度v2;v⊥为绕定滑轮转动的速度.关系式为v2=v1cos θ,θ为v1与v∥间的夹角.当A上升至与定滑轮的连线处于水平位置时,θ=90°,cos θ=0,即此时v2=0,D项正确.
同课章节目录
- 第一章 抛体运动
- 1 认识曲线运动
- 2 运动的合成与分解
- 3 探究平抛运动的特点
- 4 研究平抛运动的规律
- 5 斜抛运动(选学)
- 第二章 匀速圆周运动
- 1 圆周运动
- 2 匀速圆周运动的向心力和向心加速度
- 3 圆周运动的实例分析
- 4 圆周运动与人类文明(选学)
- 第三章 万有引力定律
- 1 天体运动
- 2 万有引力定律
- 3 预言未知星体 计算天体质量
- 4 人造卫星宇宙
- 5 太空探索(选学)
- 第四章 机械能及其守恒定律
- 1 功
- 2 功率
- 3 动能 动能定理
- 4 势能
- 5 机械能守恒定律
- 6 实验:验证机械能守恒定律
- 第五章 经典力学的局限性与相对论初步
- 1 经典力学的成就与局限性
- 2 相对论时空观简介
- 3 宇宙的起源和演化
