《6.6简单几何体的再认识》第2课时课件2022-2023学年高一下学期数学北师大版(2019)必修二(共16张PPT)
文档属性
| 名称 | 《6.6简单几何体的再认识》第2课时课件2022-2023学年高一下学期数学北师大版(2019)必修二(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 608.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 13:14:16 | ||
图片预览






文档简介
(共16张PPT)
6.6 简单几何体的再认识
第2课时
导入新课
问题1 前面我们学习了柱、锥、台的展开与面积计算,把简单组合体分割成几个几何体,其表面积如何变化?其体积呢?
表面积变大了,体积不变.
新知探究
问题2 长方体、正方体、圆柱的体积公式如何表示?根据这些体积公式,推测柱体的体积计算公式.
V长方体=abc,V正方体=a3,V圆柱=πr2h,
根据这些体积公式可知:设柱体的底面面积为S,高为h,则柱体的体积公式为V柱体=Sh.
问题3 圆锥的体积公式如何表示?根据圆锥的体积公式,推测锥体的体积计算公式.
V圆锥= πr2h,V锥体= Sh(S为底面面积,h为高).
新知探究
问题4 柱、锥、台体的体积公式之间有什么关系吗?
其中S上、S下分别为台体的上、下底面面积,h为高,S为柱或锥体底面面积.
S上=S下
S上=0
V柱体=Sh
V锥体=
初步应用
例1 埃及胡夫金字塔大约建于公元前2580年,其形状为正四棱锥.塔高约146.6m,底面边长约230.4m.求这座金字塔的侧面积和体积.(精确到0.1)
解析:如图,高AC的长为146.6m,底面的边长为230.4m,BC的长为115.2m.
答:金字塔的侧面积约为85914.9m2,体积约为2594046.0m3.
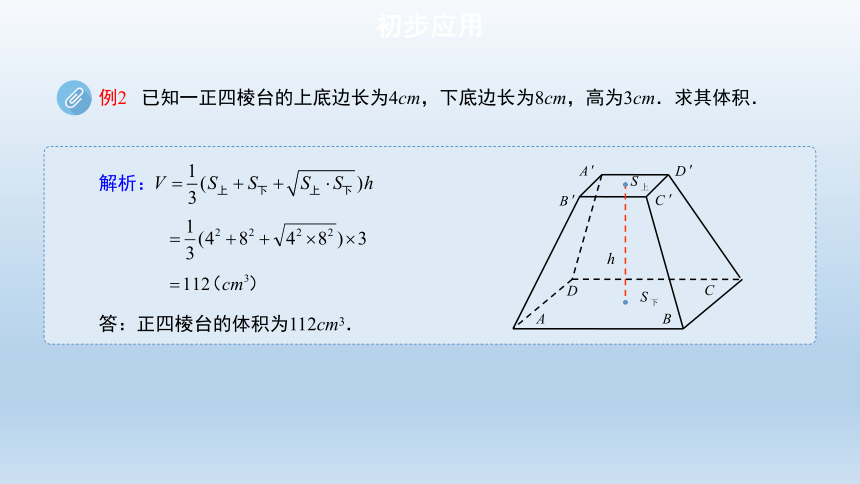
例2 已知一正四棱台的上底边长为4cm,下底边长为8cm,高为3cm.求其体积.
初步应用
答:正四棱台的体积为112cm3.
解析:
初步应用
例3 已知直四棱柱的底面为菱形,两个对角面的面积分别为2cm2,cm2,侧棱长为2cm,求其体积.
解析:设底面菱形的对角线AC,BD的长分别为xcm,ycm.
由于该棱柱是直棱柱,所以两个对角面AC1,BD1为矩形,
得到:
解得: .
所以底面菱形的面积:S= (cm2),
所以棱柱的体积:V=Sh= (cm3).
B
B1
C
C1
A
D
A1
D1
练习1 某小区修建一个圆台形的花台,它的两底面半径分别为1m和2m,高为1m,问:需要
多少立方米土才能把花台填满?(结果用π表示).
课堂练习
解析:
答:需要 土才能把花台填满.
课堂练习
练习2 一块正方形薄铁片的边长是a,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形,用这块扇形铁板围成一个圆锥筒,求它的容积.
解析:扇形的弧长:
圆锥筒的底面周长:
解得圆锥筒的底面半径:
所以圆锥筒的高:
圆锥筒的体积:
归纳小结
(1)求台体体积的关键是什么?
(2)求锥体体积常用的方法有哪些?
问题3 本节课我们学习了简单几何体柱、锥、台的体积计算,请你通过下列问题,
归纳所学知识.
(1)求台体的体积,其关键在于求高;一般地,把高放在直角梯形中求解.
常用方法为割补法和等积变换法.
①割补法:求一个组合体的体积可以将这个组合体分割成几个柱体、锥体(或补成一个
(2)方法有:求锥体的体积,要选择适当的底面和高,然后应用公式V= Sh进行计算;
柱体或锥体),求出柱体和锥体的体积,从而得出几何体的体积.
②等积变换法:三棱锥的任一个面可作为三棱锥的底面.
求体积时,可选择容易计算的方法来计算.
作业布置
作业:教科书第244页,A组第3题,第5题,第8题;B组第1题,第3题.
1
目标检测
D
正四棱柱的底面积为P,过相对侧棱截面的面积为Q,则它的体积是( )
A.
B.
C.
D.
解析:设正四棱柱的底面边长、高分别为a、h,则P=a2,Q=.
故选:D.
故V=a2h=a·ah=
2
目标检测
C
已知圆锥的母线长是8,底面周长为6π,则它的体积是( )
A.
B.
C.
D.
解析:设圆锥底面圆的半径为r,则2πr=6π,
设圆锥的高为h,则h=,
∴r=3.
∴V圆锥= .
故选:C.
3
目标检测
一个长方体的三个面的面积分别是,,,则这个长方体的体积为________.
解析:设长方体的棱长分别为a,b,c,
则
三式相乘可知(abc)2=6,
所以长方体的体积V=abc=.
故答案为:.
4
目标检测
如图,所示的是一个底面直径为20cm的装有一部分水的圆柱形玻璃杯,水面下放着一个底面直径为6cm,高为20cm的圆锥形铅锤.当铅锤从水中取出后,杯里的水将下降多少?(π≈3.14)
解析:因为玻璃杯是圆柱形的,
这个圆柱的底面与玻璃杯的底面相同,是一直径为20cm的圆,
它的体积正好等于圆锥形铅锤的体积,这个小圆柱的高就是水面下降的高度.
所以铅锤取出后,水面下降部分实际上是一个小圆柱,
圆锥形铅锤的体积为 =60π(cm3).
4
目标检测
如图,所示的是一个底面直径为20cm的装有一部分水的圆柱形玻璃杯,水面下放着一个底面直径为6cm,高为20cm的圆锥形铅锤.当铅锤从水中取出后,杯里的水将下降多少?(π≈3.14)
解析:设水面下降的高度为xcm,
则小圆柱的体积为π×(20÷2)2×x=100πx(cm3) ,
所以60π=100πx,解得x=0.6,
即铅锤取出后,杯中水将下降0.6cm.
6.6 简单几何体的再认识
第2课时
导入新课
问题1 前面我们学习了柱、锥、台的展开与面积计算,把简单组合体分割成几个几何体,其表面积如何变化?其体积呢?
表面积变大了,体积不变.
新知探究
问题2 长方体、正方体、圆柱的体积公式如何表示?根据这些体积公式,推测柱体的体积计算公式.
V长方体=abc,V正方体=a3,V圆柱=πr2h,
根据这些体积公式可知:设柱体的底面面积为S,高为h,则柱体的体积公式为V柱体=Sh.
问题3 圆锥的体积公式如何表示?根据圆锥的体积公式,推测锥体的体积计算公式.
V圆锥= πr2h,V锥体= Sh(S为底面面积,h为高).
新知探究
问题4 柱、锥、台体的体积公式之间有什么关系吗?
其中S上、S下分别为台体的上、下底面面积,h为高,S为柱或锥体底面面积.
S上=S下
S上=0
V柱体=Sh
V锥体=
初步应用
例1 埃及胡夫金字塔大约建于公元前2580年,其形状为正四棱锥.塔高约146.6m,底面边长约230.4m.求这座金字塔的侧面积和体积.(精确到0.1)
解析:如图,高AC的长为146.6m,底面的边长为230.4m,BC的长为115.2m.
答:金字塔的侧面积约为85914.9m2,体积约为2594046.0m3.
例2 已知一正四棱台的上底边长为4cm,下底边长为8cm,高为3cm.求其体积.
初步应用
答:正四棱台的体积为112cm3.
解析:
初步应用
例3 已知直四棱柱的底面为菱形,两个对角面的面积分别为2cm2,cm2,侧棱长为2cm,求其体积.
解析:设底面菱形的对角线AC,BD的长分别为xcm,ycm.
由于该棱柱是直棱柱,所以两个对角面AC1,BD1为矩形,
得到:
解得: .
所以底面菱形的面积:S= (cm2),
所以棱柱的体积:V=Sh= (cm3).
B
B1
C
C1
A
D
A1
D1
练习1 某小区修建一个圆台形的花台,它的两底面半径分别为1m和2m,高为1m,问:需要
多少立方米土才能把花台填满?(结果用π表示).
课堂练习
解析:
答:需要 土才能把花台填满.
课堂练习
练习2 一块正方形薄铁片的边长是a,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形,用这块扇形铁板围成一个圆锥筒,求它的容积.
解析:扇形的弧长:
圆锥筒的底面周长:
解得圆锥筒的底面半径:
所以圆锥筒的高:
圆锥筒的体积:
归纳小结
(1)求台体体积的关键是什么?
(2)求锥体体积常用的方法有哪些?
问题3 本节课我们学习了简单几何体柱、锥、台的体积计算,请你通过下列问题,
归纳所学知识.
(1)求台体的体积,其关键在于求高;一般地,把高放在直角梯形中求解.
常用方法为割补法和等积变换法.
①割补法:求一个组合体的体积可以将这个组合体分割成几个柱体、锥体(或补成一个
(2)方法有:求锥体的体积,要选择适当的底面和高,然后应用公式V= Sh进行计算;
柱体或锥体),求出柱体和锥体的体积,从而得出几何体的体积.
②等积变换法:三棱锥的任一个面可作为三棱锥的底面.
求体积时,可选择容易计算的方法来计算.
作业布置
作业:教科书第244页,A组第3题,第5题,第8题;B组第1题,第3题.
1
目标检测
D
正四棱柱的底面积为P,过相对侧棱截面的面积为Q,则它的体积是( )
A.
B.
C.
D.
解析:设正四棱柱的底面边长、高分别为a、h,则P=a2,Q=.
故选:D.
故V=a2h=a·ah=
2
目标检测
C
已知圆锥的母线长是8,底面周长为6π,则它的体积是( )
A.
B.
C.
D.
解析:设圆锥底面圆的半径为r,则2πr=6π,
设圆锥的高为h,则h=,
∴r=3.
∴V圆锥= .
故选:C.
3
目标检测
一个长方体的三个面的面积分别是,,,则这个长方体的体积为________.
解析:设长方体的棱长分别为a,b,c,
则
三式相乘可知(abc)2=6,
所以长方体的体积V=abc=.
故答案为:.
4
目标检测
如图,所示的是一个底面直径为20cm的装有一部分水的圆柱形玻璃杯,水面下放着一个底面直径为6cm,高为20cm的圆锥形铅锤.当铅锤从水中取出后,杯里的水将下降多少?(π≈3.14)
解析:因为玻璃杯是圆柱形的,
这个圆柱的底面与玻璃杯的底面相同,是一直径为20cm的圆,
它的体积正好等于圆锥形铅锤的体积,这个小圆柱的高就是水面下降的高度.
所以铅锤取出后,水面下降部分实际上是一个小圆柱,
圆锥形铅锤的体积为 =60π(cm3).
4
目标检测
如图,所示的是一个底面直径为20cm的装有一部分水的圆柱形玻璃杯,水面下放着一个底面直径为6cm,高为20cm的圆锥形铅锤.当铅锤从水中取出后,杯里的水将下降多少?(π≈3.14)
解析:设水面下降的高度为xcm,
则小圆柱的体积为π×(20÷2)2×x=100πx(cm3) ,
所以60π=100πx,解得x=0.6,
即铅锤取出后,杯中水将下降0.6cm.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
