《4.1同角三角函数的基本关系》第2课时课件2022-2023学年高一下学期数学北师大版(2019)必修二(共20张PPT)
文档属性
| 名称 | 《4.1同角三角函数的基本关系》第2课时课件2022-2023学年高一下学期数学北师大版(2019)必修二(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 493.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
同角三角函数的基本关系
第2课时
导入新课
问题1 我们学习了哪些同角三角函数的基本关系式?它有哪些变式?
(2)变形公式:sin2α=1-cos2α;cos2α=1-sin2α;
(1)同角关系式:sin2α+cos2α=1,tanα= .
sinα=cosαtanα;cosα= .
新知探究
问题2 sinα+cosα,sinα-cosα,sinαcosα这三个式子之间有什么关系呢?
(sinα±cosα)2=1±2sinαcosα.
新知探究
追问:若已知sinα-cosα= ,π<α< ,如何求tanα呢?
sinα-cosα= <0 ①
将①式两边平方得sinαcosα= ,
所以sinα<0,cosα<0,
又∵π<α< ,
故sinα+cosα<0,
∴sin α+cos α= ②
∴tanα= .
由①+②式得,
新知探究
因为α是第二象限角,所以sinα>0,cosα<0.
问题3 如何化简 ,其中α是第二象限角呢?
故
新知探究
追问:通过问题3,你能总结化简过程中常用的方法吗?
(1)化切为弦,即把非正弦、余弦函数都化为正弦、余弦函数.从而减少函数名称,
达到化简的目的.
(2)对于含有根号的,常把根号下化成完全平方式,然后去根号达到化简的目的.
(3)对于化简含高次的三角函数式,往往借助于因式分解,或构造sin2α+cos2α=1,
以降低函数次数,达到化简的目的.
新知探究
问题4 如何证明 ?
分析等式的左右两端,发现利用平方关系可以证明.
因为sin2α+cos2α=1,
由已知可知cosα≠0,且1-sinα≠0,
把①式的两端同除以cosα(1-sinα),
所以cos2α=1-sin2α=(1-sinα)(1+sinα) ①
得 .
新知探究
追问:证明等式有哪些常用方法?
(1)从一边开始,证得它等于另一边.
(2)证明左右两边都等于同一个式子.
(3)变更论证,即通过化除为乘、左右相减等,转化成证明与其等价的等式.
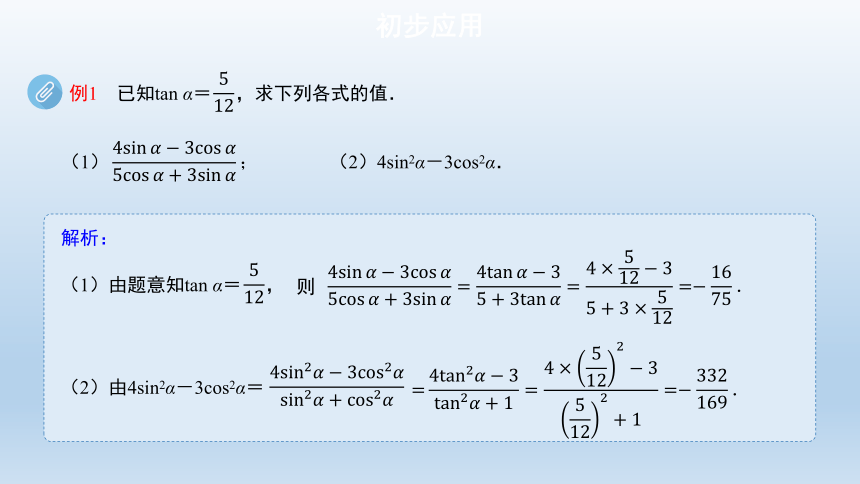
例1 已知tan α= ,求下列各式的值.
初步应用
(1)
(2)4sin2α-3cos2α.
(2)由4sin2α-3cos2α=
(1)由题意知tan α= ,
则
解析:
初步应用
已知tan α=m,可以求 或
的值,将分子分母同除以cos α或cos2α,化成关于tan α的式子,从而达到求值的目的.
方法总结
例2 (1)化简:
初步应用
(2)化简:
,(0<α< ).
(1)原式
解析:
例2 (1)化简:
初步应用
(2)化简:
,(0<α< ).
(2)原式
所以 >0, >0,
初步应用
利用同角三角函数关系化简的常用方法:
①化切为弦,减少函数名称,便于约分化简.
②对含根号的,应先把被开方式化为完全平方,去掉根号,
为防止出错,去掉根号后首先用绝对值表示,然后考虑正负.
③对含有高次的三角函数式,可借助于因式分解,或构造平方关系,以便于降幂化简.
初步应用
例3 求证:
简单的三角恒等式的证明思路:
(1)从一边开始,证明它等于另一边.
(2)证明左、右两边等于同一个式子.
(3)逐步寻找等式成立的条件,达到由繁到简.
等式左边=
等式右边=
故等式得证.
归纳小结
(1)对三角函数式化简的原则是什么?
(2)利用(sin α±cos α)2=1±2sinαcosα,求sinα+cosα或sinα-cosα的值时,
要注意什么?
问题5 回归本节的学习,你有什么收获?可以从以下几个问题归纳.
(1)①使三角函数式的次数尽量低;
③使三角函数的种类尽量少;
⑤使式中尽量不含有根号和绝对值符号;
⑥能求值的要求出具体的值,否则就用三角函数式来表示.
②使式中的项数尽量少;
④使式中的分母尽量不含有三角函数;
(2)要注意判断它们的符号.
作业布置
作业:教科书P142页,A组第3题,B组第1,2,3题.
1
目标检测
B
化简(1+tan2α) cos2α=( )
A.0
B.1
C.2
D.3
解析:原式= cos2α=cos2α+sin2α=1.
2
目标检测
B
sinαcosα= ,且 ,则cosα-sinα的值为( )
A.
C.
D.
B.
∴cos α-sin α=± .
解析:∵(cos α-sin α)2=sin2α-2sin αcos α+cos2α=1-2× ,
又 ,故sin α>cos α,
∴cos α-sin α= .
3
目标检测
若tan(π+α)=2,则 =______.
解析:因为tan(π+α)=2,所以tanα=2,
所以,原式
上式分子分母同除以cos α得,
4
目标检测
证明:
证明:左边
=右边,故原等式成立.
同角三角函数的基本关系
第2课时
导入新课
问题1 我们学习了哪些同角三角函数的基本关系式?它有哪些变式?
(2)变形公式:sin2α=1-cos2α;cos2α=1-sin2α;
(1)同角关系式:sin2α+cos2α=1,tanα= .
sinα=cosαtanα;cosα= .
新知探究
问题2 sinα+cosα,sinα-cosα,sinαcosα这三个式子之间有什么关系呢?
(sinα±cosα)2=1±2sinαcosα.
新知探究
追问:若已知sinα-cosα= ,π<α< ,如何求tanα呢?
sinα-cosα= <0 ①
将①式两边平方得sinαcosα= ,
所以sinα<0,cosα<0,
又∵π<α< ,
故sinα+cosα<0,
∴sin α+cos α= ②
∴tanα= .
由①+②式得,
新知探究
因为α是第二象限角,所以sinα>0,cosα<0.
问题3 如何化简 ,其中α是第二象限角呢?
故
新知探究
追问:通过问题3,你能总结化简过程中常用的方法吗?
(1)化切为弦,即把非正弦、余弦函数都化为正弦、余弦函数.从而减少函数名称,
达到化简的目的.
(2)对于含有根号的,常把根号下化成完全平方式,然后去根号达到化简的目的.
(3)对于化简含高次的三角函数式,往往借助于因式分解,或构造sin2α+cos2α=1,
以降低函数次数,达到化简的目的.
新知探究
问题4 如何证明 ?
分析等式的左右两端,发现利用平方关系可以证明.
因为sin2α+cos2α=1,
由已知可知cosα≠0,且1-sinα≠0,
把①式的两端同除以cosα(1-sinα),
所以cos2α=1-sin2α=(1-sinα)(1+sinα) ①
得 .
新知探究
追问:证明等式有哪些常用方法?
(1)从一边开始,证得它等于另一边.
(2)证明左右两边都等于同一个式子.
(3)变更论证,即通过化除为乘、左右相减等,转化成证明与其等价的等式.
例1 已知tan α= ,求下列各式的值.
初步应用
(1)
(2)4sin2α-3cos2α.
(2)由4sin2α-3cos2α=
(1)由题意知tan α= ,
则
解析:
初步应用
已知tan α=m,可以求 或
的值,将分子分母同除以cos α或cos2α,化成关于tan α的式子,从而达到求值的目的.
方法总结
例2 (1)化简:
初步应用
(2)化简:
,(0<α< ).
(1)原式
解析:
例2 (1)化简:
初步应用
(2)化简:
,(0<α< ).
(2)原式
所以 >0, >0,
初步应用
利用同角三角函数关系化简的常用方法:
①化切为弦,减少函数名称,便于约分化简.
②对含根号的,应先把被开方式化为完全平方,去掉根号,
为防止出错,去掉根号后首先用绝对值表示,然后考虑正负.
③对含有高次的三角函数式,可借助于因式分解,或构造平方关系,以便于降幂化简.
初步应用
例3 求证:
简单的三角恒等式的证明思路:
(1)从一边开始,证明它等于另一边.
(2)证明左、右两边等于同一个式子.
(3)逐步寻找等式成立的条件,达到由繁到简.
等式左边=
等式右边=
故等式得证.
归纳小结
(1)对三角函数式化简的原则是什么?
(2)利用(sin α±cos α)2=1±2sinαcosα,求sinα+cosα或sinα-cosα的值时,
要注意什么?
问题5 回归本节的学习,你有什么收获?可以从以下几个问题归纳.
(1)①使三角函数式的次数尽量低;
③使三角函数的种类尽量少;
⑤使式中尽量不含有根号和绝对值符号;
⑥能求值的要求出具体的值,否则就用三角函数式来表示.
②使式中的项数尽量少;
④使式中的分母尽量不含有三角函数;
(2)要注意判断它们的符号.
作业布置
作业:教科书P142页,A组第3题,B组第1,2,3题.
1
目标检测
B
化简(1+tan2α) cos2α=( )
A.0
B.1
C.2
D.3
解析:原式= cos2α=cos2α+sin2α=1.
2
目标检测
B
sinαcosα= ,且 ,则cosα-sinα的值为( )
A.
C.
D.
B.
∴cos α-sin α=± .
解析:∵(cos α-sin α)2=sin2α-2sin αcos α+cos2α=1-2× ,
又 ,故sin α>cos α,
∴cos α-sin α= .
3
目标检测
若tan(π+α)=2,则 =______.
解析:因为tan(π+α)=2,所以tanα=2,
所以,原式
上式分子分母同除以cos α得,
4
目标检测
证明:
证明:左边
=右边,故原等式成立.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
