1.3.2 平抛运动 课时二(平抛与斜面)(课件) (14张PPT)高一物理同步精品课堂(教科版2019 必修第二册)
文档属性
| 名称 | 1.3.2 平抛运动 课时二(平抛与斜面)(课件) (14张PPT)高一物理同步精品课堂(教科版2019 必修第二册) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-07 21:20:12 | ||
图片预览




文档简介
1.3.2
平抛运动二(斜面专题)
【知识归纳】
思路:解答时要充分运用斜面倾角,找出斜面倾角同位移和速度与水平方向夹角的关系是解题的关键。
解决平抛运动的方法是分解,若知道末速度方向,则分解末速度;若知道位移方向,则分解位移。
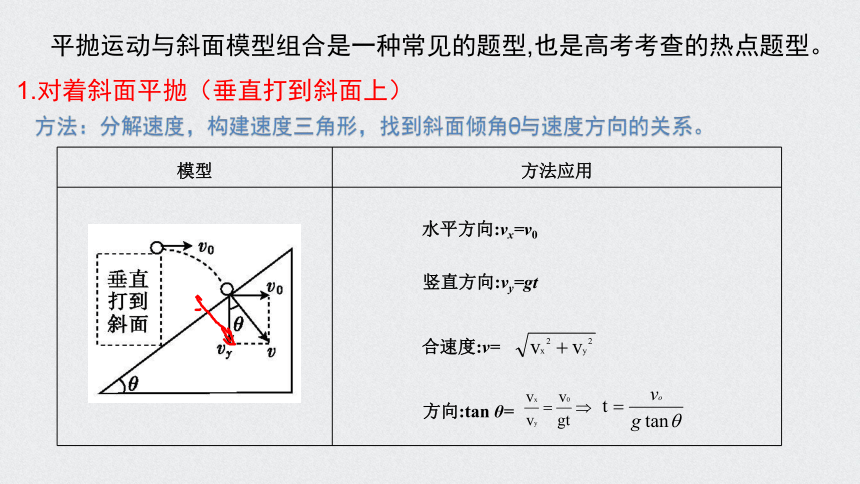
平抛运动与斜面模型组合是一种常见的题型,也是高考考查的热点题型。1.对着斜面平抛(垂直打到斜面上)
模型
方法应用
水平方向:vx=v0
竖直方向:vy=gt
合速度:v=
方向:tan θ=
方法:分解速度,构建速度三角形,找到斜面倾角θ与速度方向的关系。
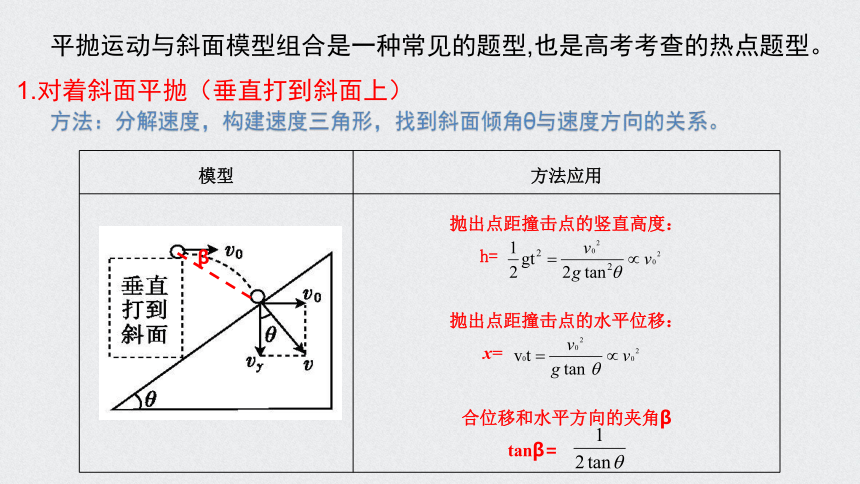
平抛运动与斜面模型组合是一种常见的题型,也是高考考查的热点题型。1.对着斜面平抛(垂直打到斜面上)
模型
方法应用
抛出点距撞击点的竖直高度:
h=
抛出点距撞击点的水平位移:
x=
合位移和水平方向的夹角β
tanβ=
β
方法:分解速度,构建速度三角形,找到斜面倾角θ与速度方向的关系。
A
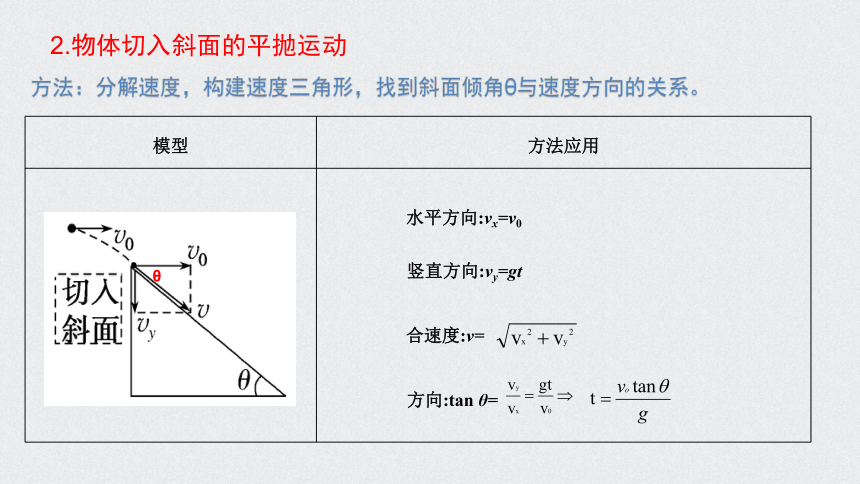
2.物体切入斜面的平抛运动
模型
方法应用
水平方向:vx=v0
竖直方向:vy=gt
合速度:v=
方向:tan θ=
方法:分解速度,构建速度三角形,找到斜面倾角θ与速度方向的关系。
θ
15m 10√3m
?
3.顺着斜面水平抛出(落在斜面)
模型
方法应用
水平:x=v0t =s·cosθ
竖直:y=gt2 =s·sinθ
合位移:s=
方向:tan θ=
方法:分解位移,构建位移三角形;隐含条件:斜面倾角θ等于位移与水平方向的夹角。
例4
c
例5
D
例6
c
规律总结
从斜面上某点水平抛出,又落到斜面上的平抛运动的五个特点
(1)位移方向相同,竖直位移与水平位移之比等于斜面倾斜角的正切值。
★(2)末速度方向平行(即末速度方向相同),竖直分速度与水平分速度(初速度)之比等于斜面倾斜角正切值的2倍。
(3)运动的时间与初速度成正比?。
(4)位移与初速度的二次方成正比?。
★(5)当速度与斜面平行时,物体到斜面的距离最远,且从抛出到距斜
面最远所用的时间为平抛运动时间的一半。
【补充训练】跳台滑雪是一项勇敢者的运动,它需要利用山势特点建造一个特殊跳台.一运动员穿着专用滑雪板,不带雪杖,在滑雪道上获得较高速度后从A点沿水平方向飞出,在空中飞行一段距离后在山坡上B点着陆,如图2所示.已知可视为质点的运动员从A点水平飞出的速度v0=20 m/s,山坡可看成倾角为37°的斜面,不考虑空气阻力(g=10 m/s2,sin 37°=0.6,cos 37°=0.8),求:
(1)运动员在空中的飞行时间t1;
(2)运动员从飞出至落在斜面上的位移大小s;
(3)运动员落到斜面上时的速度大小v;
(4)运动员何时离斜面最远.最远距离是多少?
解:⑴⑵运动员从A点到B点做平抛运动,
水平方向的位移:x=v0t1
竖直方向的位移:y=????????gt12
又有tan 37°=????????
代入数据解得:t1=3 s,x=60 m,y=45 m.
运动员从飞出至落在斜面上的位移大小s=????????+????????=75 m.
?
(3)运动员落在斜面上时速度的竖直分量vy=gt1=10×3 m/s=30 m/s,
运动员落到斜面上时的速度大小v= ????????????+?????????????=10 ????????m/s.
?
(4)如图,运动员距离斜面最远时,合速度方向与斜面平行,tan 37°=?????????????????,即tan 37°=????????????????????,
解得t2=?????????????????????????°????=1.5 s.
平抛运动二(斜面专题)
【知识归纳】
思路:解答时要充分运用斜面倾角,找出斜面倾角同位移和速度与水平方向夹角的关系是解题的关键。
解决平抛运动的方法是分解,若知道末速度方向,则分解末速度;若知道位移方向,则分解位移。
平抛运动与斜面模型组合是一种常见的题型,也是高考考查的热点题型。1.对着斜面平抛(垂直打到斜面上)
模型
方法应用
水平方向:vx=v0
竖直方向:vy=gt
合速度:v=
方向:tan θ=
方法:分解速度,构建速度三角形,找到斜面倾角θ与速度方向的关系。
平抛运动与斜面模型组合是一种常见的题型,也是高考考查的热点题型。1.对着斜面平抛(垂直打到斜面上)
模型
方法应用
抛出点距撞击点的竖直高度:
h=
抛出点距撞击点的水平位移:
x=
合位移和水平方向的夹角β
tanβ=
β
方法:分解速度,构建速度三角形,找到斜面倾角θ与速度方向的关系。
A
2.物体切入斜面的平抛运动
模型
方法应用
水平方向:vx=v0
竖直方向:vy=gt
合速度:v=
方向:tan θ=
方法:分解速度,构建速度三角形,找到斜面倾角θ与速度方向的关系。
θ
15m 10√3m
?
3.顺着斜面水平抛出(落在斜面)
模型
方法应用
水平:x=v0t =s·cosθ
竖直:y=gt2 =s·sinθ
合位移:s=
方向:tan θ=
方法:分解位移,构建位移三角形;隐含条件:斜面倾角θ等于位移与水平方向的夹角。
例4
c
例5
D
例6
c
规律总结
从斜面上某点水平抛出,又落到斜面上的平抛运动的五个特点
(1)位移方向相同,竖直位移与水平位移之比等于斜面倾斜角的正切值。
★(2)末速度方向平行(即末速度方向相同),竖直分速度与水平分速度(初速度)之比等于斜面倾斜角正切值的2倍。
(3)运动的时间与初速度成正比?。
(4)位移与初速度的二次方成正比?。
★(5)当速度与斜面平行时,物体到斜面的距离最远,且从抛出到距斜
面最远所用的时间为平抛运动时间的一半。
【补充训练】跳台滑雪是一项勇敢者的运动,它需要利用山势特点建造一个特殊跳台.一运动员穿着专用滑雪板,不带雪杖,在滑雪道上获得较高速度后从A点沿水平方向飞出,在空中飞行一段距离后在山坡上B点着陆,如图2所示.已知可视为质点的运动员从A点水平飞出的速度v0=20 m/s,山坡可看成倾角为37°的斜面,不考虑空气阻力(g=10 m/s2,sin 37°=0.6,cos 37°=0.8),求:
(1)运动员在空中的飞行时间t1;
(2)运动员从飞出至落在斜面上的位移大小s;
(3)运动员落到斜面上时的速度大小v;
(4)运动员何时离斜面最远.最远距离是多少?
解:⑴⑵运动员从A点到B点做平抛运动,
水平方向的位移:x=v0t1
竖直方向的位移:y=????????gt12
又有tan 37°=????????
代入数据解得:t1=3 s,x=60 m,y=45 m.
运动员从飞出至落在斜面上的位移大小s=????????+????????=75 m.
?
(3)运动员落在斜面上时速度的竖直分量vy=gt1=10×3 m/s=30 m/s,
运动员落到斜面上时的速度大小v= ????????????+?????????????=10 ????????m/s.
?
(4)如图,运动员距离斜面最远时,合速度方向与斜面平行,tan 37°=?????????????????,即tan 37°=????????????????????,
解得t2=?????????????????????????°????=1.5 s.
同课章节目录
- 第一章 抛体运动
- 1 认识曲线运动
- 2 运动的合成与分解
- 3 探究平抛运动的特点
- 4 研究平抛运动的规律
- 5 斜抛运动(选学)
- 第二章 匀速圆周运动
- 1 圆周运动
- 2 匀速圆周运动的向心力和向心加速度
- 3 圆周运动的实例分析
- 4 圆周运动与人类文明(选学)
- 第三章 万有引力定律
- 1 天体运动
- 2 万有引力定律
- 3 预言未知星体 计算天体质量
- 4 人造卫星宇宙
- 5 太空探索(选学)
- 第四章 机械能及其守恒定律
- 1 功
- 2 功率
- 3 动能 动能定理
- 4 势能
- 5 机械能守恒定律
- 6 实验:验证机械能守恒定律
- 第五章 经典力学的局限性与相对论初步
- 1 经典力学的成就与局限性
- 2 相对论时空观简介
- 3 宇宙的起源和演化
