2023年广东省普通高中学业水平合格性考试数学复习讲义第七章 立体几何 学案
文档属性
| 名称 | 2023年广东省普通高中学业水平合格性考试数学复习讲义第七章 立体几何 学案 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 00:00:00 | ||
图片预览



文档简介
21世纪教育网 –全国领先的中小学教育资源及组卷应用平台
第七章 立体几何
1.圆柱、圆锥、圆台的侧面展开图及侧面积公式
圆柱 圆锥 圆台
侧面展开图
侧面积公式 S圆柱侧=2πrl S圆锥侧=πrl S圆台侧=π(r+r′)l
2.空间几何体的表面积与体积公式
名称几何体 表面积 体积
柱体(棱柱和圆柱) S表面积=S侧+2S底 V=Sh
锥体(棱锥和圆锥) S表面积=S侧+S底 V=Sh
球 S=4πr2 V=πr3
3.直线与平面平行的判定定理和性质定理
文字语言 图形语言 符号语言
判定定理 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行(线线平行 线面平行) ∵l∥a,a α,lα,∴l∥α
性质定理 一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行 线线平行”) ∵l∥α,l β,α∩β=b,∴l∥b
4.平面与平面平行的判定定理和性质定理
文字语言 图形语言 符号语言
判定定理 一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为“线面平行 面面平行”) ∵a∥β,b∥β,a∩b=P,a α,b α,∴α∥β
性质定理 如果两个平行平面同时和第三个平面相交,那么它们的交线平行 ∵α∥β,α∩γ=a,β∩γ=b,∴a∥b
5.与垂直相关的平行的判定
(1)a⊥α,b⊥α a∥b.
(2)a⊥α,a⊥β α∥β.
6.平行问题的转化关系
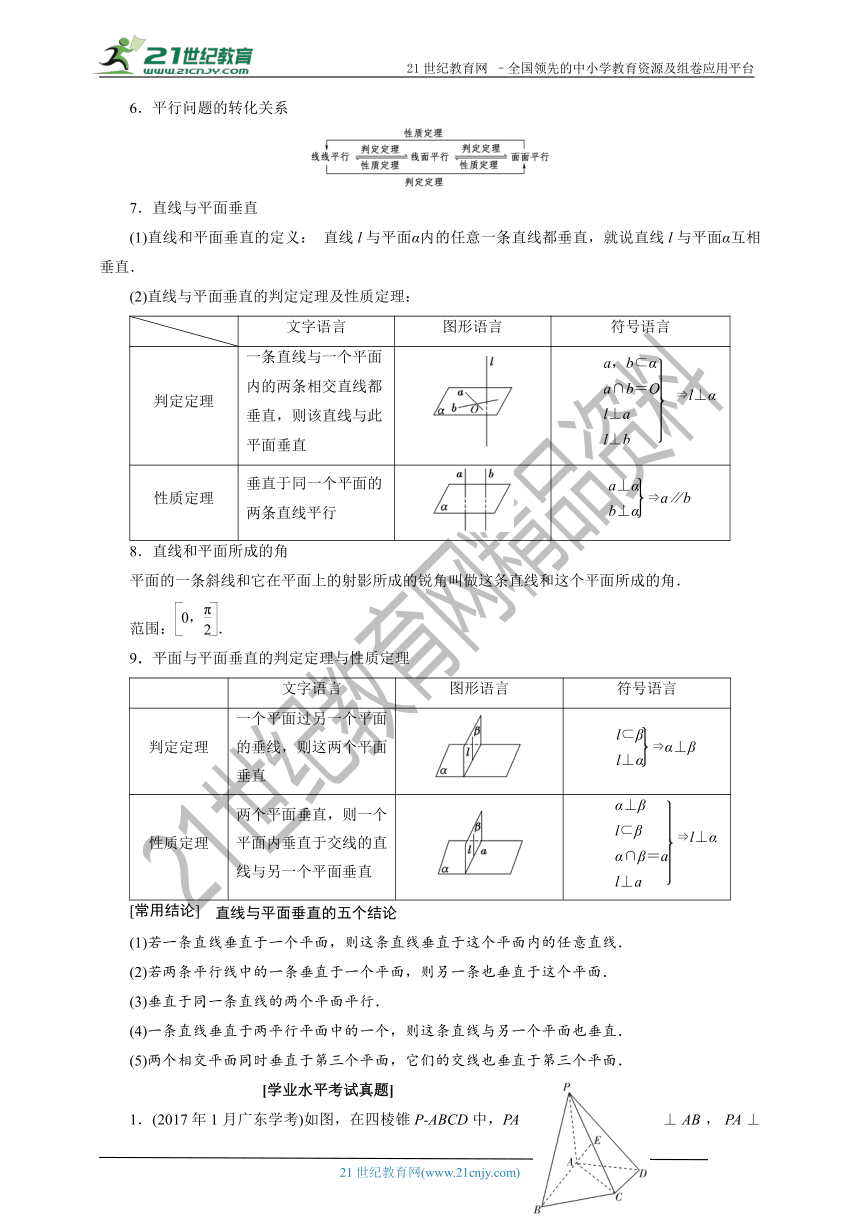
7.直线与平面垂直
(1)直线和平面垂直的定义: 直线l与平面α内的任意一条直线都垂直,就说直线l与平面α互相垂直.
(2)直线与平面垂直的判定定理及性质定理:
文字语言 图形语言 符号语言
判定定理 一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直 l⊥α
性质定理 垂直于同一个平面的两条直线平行 a∥b
8.直线和平面所成的角
平面的一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角.
范围:.
9.平面与平面垂直的判定定理与性质定理
文字语言 图形语言 符号语言
判定定理 一个平面过另一个平面的垂线,则这两个平面垂直 α⊥β
性质定理 两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直 l⊥α
直线与平面垂直的五个结论
(1)若一条直线垂直于一个平面,则这条直线垂直于这个平面内的任意直线.
(2)若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.
(3)垂直于同一条直线的两个平面平行.
(4)一条直线垂直于两平行平面中的一个,则这条直线与另一个平面也垂直.
(5)两个相交平面同时垂直于第三个平面,它们的交线也垂直于第三个平面.
[学业水平考试真题]
1.(2017年1月广东学考)如图,在四棱锥P-ABCD中,PA⊥AB,PA⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC=2,E为PC的中点.
(1) 证明:AP⊥CD;
(2) 求三棱锥P-ABC的体积;
(3) 证明:AE⊥平面PCD.
2.(2018年1月广东学考)如图所示,一个空间几何体的正视图和侧视图都是矩形,俯视图是正方形,则该几何体的体积为( )
A.1 B.2 C.4 D.8
3.(2018年1月广东学考)如图所示,在三棱锥P -ABC中,PA⊥平面ABC,PB=BC,F为BC的中点,DE垂直平分PC,且DE分别交AC,PC于点D,E.
(1)证明:EF∥平面ABP;
(2)证明:BD⊥AC.
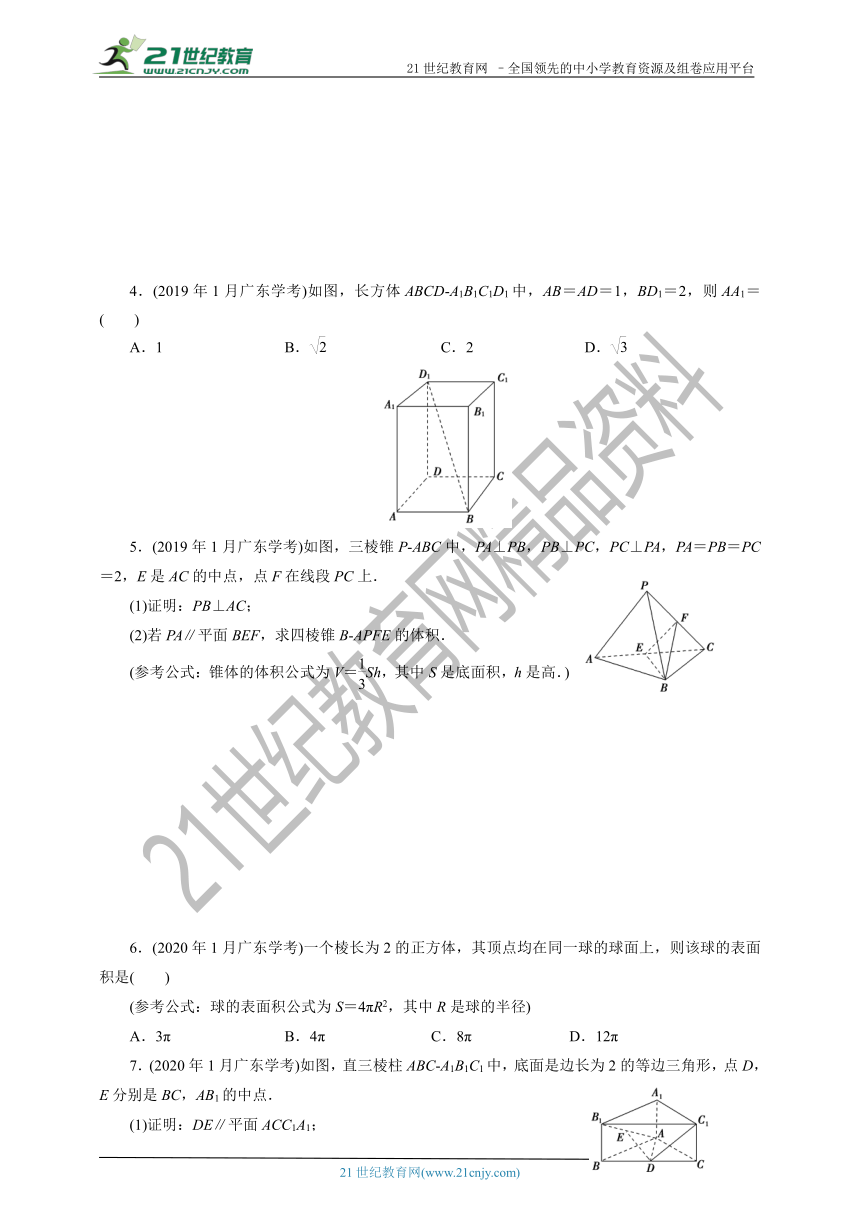
4.(2019年1月广东学考)如图,长方体ABCD -A1B1C1D1中,AB=AD=1,BD1=2,则AA1=( )
A.1 B. C.2 D.
5.(2019年1月广东学考)如图,三棱锥P -ABC中,PA⊥PB,PB⊥PC,PC⊥PA,PA=PB=PC=2,E是AC的中点,点F在线段PC上.
(1)证明:PB⊥AC;
(2)若PA∥平面BEF,求四棱锥B -APFE的体积.
(参考公式:锥体的体积公式为V=Sh,其中S是底面积,h是高.)
6.(2020年1月广东学考)一个棱长为2的正方体,其顶点均在同一球的球面上,则该球的表面积是( )
(参考公式:球的表面积公式为S=4πR2,其中R是球的半径)
A.3π B.4π C.8π D.12π
7.(2020年1月广东学考)如图,直三棱柱ABC -A1B1C1中,底面是边长为2的等边三角形,点D,E分别是BC,AB1的中点.
(1)证明:DE∥平面ACC1A1;
(2)若BB1=1,证明:C1D⊥平面ADE.
8.(2021年1月广东学考)已知直线,若//,,则下列结论正确的是( )
A.// B.与是异面直线 C. D.以上均有可能
9.(2021年1月广东学考)如图3,在四棱锥中,底面ABCD是边长为2的菱形,PA=AC=2,,E,F分别为PD,BC的中点.
(1)求三棱锥的体积;
(2)证明:.
[学业水平考试最新模拟题]
1.(2019年蛇口学考模拟)如图是一个几何体的三视图,则该几何体为( )
A.球 B.圆柱 C.圆台 D.圆锥
第1题图 第2题图
2.(2018年广东省普通高中学业水平测试数学模拟测试卷(考前压题篇))若如图是一个几何体的三视图,则这个几何体是( )
A.圆锥 B.棱柱 C.圆柱 D.棱锥
3.(2019年韶关市学考模拟)某几何体的三视图如图所示,则该几何体的体积为( )
A.π B.48π C.π D.64π
4.(2020年广东学考模拟)某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )
A.8cm3 B.12cm3 C.cm3 D.cm3
5.(2019年深圳高一期末)α,β,γ为三个不重合的平面,a,b,c为三条不同的直线,则下列命题中不正确的是( )
① a∥b; ② a∥b; ③ α∥β;
④ α∥β; ⑤ α∥a; ⑥ a∥α.
A.④⑥ B.②③⑥ C.②③⑤⑥ D.②③
6.(2018年广东省普通高中数学学业水平考试模拟题)已知互相垂直的平面α,β交于直线l.若直线m,n满足m∥α,n⊥β,则( )
A.m∥l B.m∥n C.n⊥l D.m⊥n
7.(2015年浙江高考)设α,β是两个不同的平面,l,m是两条不同的直线,且l α,m β.( )
A.若l⊥β,则α⊥β B.若α⊥β,则l⊥m
C.若l∥β,则α∥β D.若α∥β,则l∥m
8.(2021年全国Ⅰ)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为( )
A. B. C. D.
9.(2016年全国Ⅱ)体积为8的正方体的顶点都在同一球面上,则该球的表面积为( )
A.12π B.π C.8π D.4π
10.已知一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为________.
11.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是AB,AD的中点,则异面直线B1C与EF所成角的大小为( )
A.30° B.45° C.60° D.90°
12.如图,已知四棱锥P -ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD.
(1)求证:AB∥平面PDC;
(2)求证:BC⊥平面PAC.
13.(2019年揭阳学考模拟)如图,在三棱锥P -ABC中,平面PAB⊥平面ABC,△PAB是等边三角形,AC⊥BC,且AC=BC=2,O,D分别是AB,PB的中点.
(1)求证:PA∥平面COD;
(2)求三棱锥P ABC的体积.
14.(2018年广东省普通高中数学学业水平考试模拟题)已知四棱锥P -ABCD中,PD⊥平面ABCD,四边形ABCD是正方形,E是PA的中点.
求证:(1)PC∥平面EBD;
(2)平面PBC⊥平面PCD.
15.(2020年广东学考模拟)在四棱锥S -ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2,BA=BS=4.
(1)证明:BD⊥平面SAD;
(2)求点C到平面SAB的距离.
参考答案
[学业水平考试真题]
1.(2017年1月广东学考)如图,在四棱锥P-ABCD中,PA⊥AB,PA⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC=2,E为PC的中点.
(1) 证明:AP⊥CD;
(2) 求三棱锥P-ABC的体积;
(3) 证明:AE⊥平面PCD.
(1)证明:因为PA⊥AB,PA⊥AD,AB 平面ABCD,AD 平面ABCD,AB∩AD=A,
所以PA⊥平面ABCD,
又CD 平面ABCD,
所以AP⊥CD.
(2)解:由(1)可知AP⊥平面ABC,
所以VP-ABC=S△ABC·AP,
又S△ABC=AB·BC·sin ∠ABC=×2×2×sin 60°=,
所以VP-ABC=××2=.
(3)证明:因为CD⊥AP,CD⊥AC,AP 平面APC,AC 平面APC,AP∩AC=A,
所以CD⊥平面APC,
又AE 平面APC,
所以CD⊥AE,
由AB=BC=2且∠ABC=60°得△ABC为等边三角形,且AC=2,
又因为AP=2,且E为PC的中点,
所以AE⊥PC,
又AE⊥CD,PC 平面PCD,CD 平面PCD,PC∩CD=C,
所以AE⊥平面PCD.
2.(2018年1月广东学考)如图所示,一个空间几何体的正视图和侧视图都是矩形,俯视图是正方形,则该几何体的体积为( C )
A.1 B.2 C.4 D.8
3.(2018年1月广东学考)如图所示,在三棱锥P -ABC中,PA⊥平面ABC,PB=BC,F为BC的中点,DE垂直平分PC,且DE分别交AC,PC于点D,E.
(1)证明:EF∥平面ABP;
(2)证明:BD⊥AC.
证明: (1)∵DE垂直平分PC,
∴E为PC的中点,
又∵F为BC的中点,
∴EF为△BCP的中位线,
∴EF∥BP,
又∵EF平面ABP,BP 平面ABP,
∴EF∥平面ABP.
(2)连接BE,
∵PB=BC,E为PC的中点,
∴PC⊥BE,
∵DE垂直平分PC,
∴PC⊥DE,
又∵BE∩DE=E,BE 平面BDE,DE 平面BDE,
∴PC⊥平面BDE,
又∵BD 平面BDE,
∴PC⊥BD,
∵PA⊥平面ABC,BD 平面ABC,
∴PA⊥BD,
又∵PC∩PA=P,PC 平面PAC,PA 平面PAC,
∴BD⊥平面PAC,
又∵AC 平面PAC,
∴BD⊥AC.
4.(2019年1月广东学考)如图,长方体ABCD -A1B1C1D1中,AB=AD=1,BD1=2,则AA1=( B )
A.1 B. C.2 D.
5.(2019年1月广东学考)如图,三棱锥P -ABC中,PA⊥PB,PB⊥PC,PC⊥PA,PA=PB=PC=2,E是AC的中点,点F在线段PC上.
(1)证明:PB⊥AC;
(2)若PA∥平面BEF,求四棱锥B -APFE的体积.
(参考公式:锥体的体积公式为V=Sh,其中S是底面积,h是高.)
(1)∵PA⊥PB,PB⊥PC,PC∩PA=P,
∴PB⊥平面PAC,
又AC 平面PAC,
∴PB⊥AC.
(2)∵PA∥平面BEF,PA 平面PAC,平面PAC∩平面BEF=EF,
∴EF∥PA,
∴四边形PAEF为梯形,
又∵PA⊥PC,
∴四边形PAEF为直角梯形,
又∵E是AC的中点,
∴F为PC的中点,
∴PF=PC=1,EF=PA=1,
∴直角梯形APFE的面积S=×PF=.
由(1)知PB⊥平面APFE.
∴四棱锥B APFE的体积V=S·PB=1.
6.(2020年1月广东学考)一个棱长为2的正方体,其顶点均在同一球的球面上,则该球的表面积是( D )
(参考公式:球的表面积公式为S=4πR2,其中R是球的半径)
A.3π B.4π C.8π D.12π
7.(2020年1月广东学考)如图,直三棱柱ABC -A1B1C1中,底面是边长为2的等边三角形,点D,E分别是BC,AB1的中点.
(1)证明:DE∥平面ACC1A1;
(2)若BB1=1,证明:C1D⊥平面ADE.
(1)证明:连接A1B,A1C,
在直三棱柱ABC-A1B1C1中,侧面ABB1A1是矩形,
因为点E是AB1的中点,
所以点E是A1B的中点,
又因为点D是BC的中点,
所以DE∥A1C,
因为DE平面ACC1A1,A1C 平面ACC1A1,
所以DE∥平面ACC1A1.
(2)连接B1D,在直三棱柱ABC A1B1C1中,
因为BB1⊥平面ABC,AD 平面ABC,
所以BB1⊥AD,
又因为底面ABC是等边三角形,D为BC的中点,
所以BC⊥AD,
又BC∩BB1=B,
所以AD⊥平面B1BCC1,
又C1D 平面B1BCC1,
所以AD⊥C1D,
由BC=2,得BD=1,又BB1=CC1=1,
所以DB1=C1D=,
所以DB+C1D2=B1C,
所以C1D⊥DB1,DB1∩AD=D,
所以C1D⊥平面ADB1,
即C1D⊥平面ADE.
8.(2021年1月广东学考)已知直线,若//,,则下列结论正确的是( D )
A.// B.与是异面直线 C. D.以上均有可能
9.(2021年1月广东学考)如图3,在四棱锥中,底面ABCD是边长为2的菱形,PA=AC=2,,E,F分别为PD,BC的中点.
(1)求三棱锥的体积;
(2)证明:.
(1)设AC与BD的交点为O, 因为底面ABCD是边长为2的菱形,
所以,因为AC=2,所以OA=OC==1,
在,故BD=2OB=2,
所以,
因为,所以为三棱锥的高h,
所以三棱锥的体积.
(2)取PA的中点G,
因为E为PD的中点,
所以,
又因为F为BC的中点,四边形ABCD为菱形,
所以,
所以,
故四边形BFEG为平行四边形,
所以BG//EF,
因为,
所以.
[学业水平考试最新模拟题]
1.(2019年蛇口学考模拟)如图是一个几何体的三视图,则该几何体为( D )
A.球 B.圆柱 C.圆台 D.圆锥
第1题图 第2题图
2.(2018年广东省普通高中学业水平测试数学模拟测试卷(考前压题篇))若如图是一个几何体的三视图,则这个几何体是( C )
A.圆锥 B.棱柱 C.圆柱 D.棱锥
3.(2019年韶关市学考模拟)某几何体的三视图如图所示,则该几何体的体积为( A )
A.π B.48π C.π D.64π
4.(2020年广东学考模拟)某几何体的三视图如图所示(单位:cm),则该几何体的体积是( C )
A.8cm3 B.12cm3 C.cm3 D.cm3
5.(2019年深圳高一期末)α,β,γ为三个不重合的平面,a,b,c为三条不同的直线,则下列命题中不正确的是( C )
① a∥b; ② a∥b; ③ α∥β;
④ α∥β; ⑤ α∥a; ⑥ a∥α.
A.④⑥ B.②③⑥ C.②③⑤⑥ D.②③
6.(2018年广东省普通高中数学学业水平考试模拟题)已知互相垂直的平面α,β交于直线l.若直线m,n满足m∥α,n⊥β,则( C )
A.m∥l B.m∥n C.n⊥l D.m⊥n
7.(2015年浙江高考)设α,β是两个不同的平面,l,m是两条不同的直线,且l α,m β.( A )
A.若l⊥β,则α⊥β B.若α⊥β,则l⊥m
C.若l∥β,则α∥β D.若α∥β,则l∥m
8.(2021年全国Ⅰ)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为( B )
A. B. C. D.
9.(2016年全国Ⅱ)体积为8的正方体的顶点都在同一球面上,则该球的表面积为( A )
A.12π B.π C.8π D.4π
10.已知一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为________.
11.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是AB,AD的中点,则异面直线B1C与EF所成角的大小为( C )
A.30° B.45° C.60° D.90°
12.如图,已知四棱锥P -ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD.
(1)求证:AB∥平面PDC;
(2)求证:BC⊥平面PAC.
(1)∵AB∥CD,CD 平面PDC,AB 平面PDC,
∴AB∥平面PDC.
(2)在直角梯形ABCD中,过点C作CE⊥AB于点E,则四边形ADCE为矩形,
∴AE=DC=1,又AB=2,
∴BE=1,
在Rt△BEC中,∠ABC=45°,
∴CE=BE=1,CB=,
在Rt△ACE中,AC==,
∴AC2+BC2=AB2,
∴BC⊥AC,
又PA⊥平面ABCD,BC 平面ABCD,
∴BC⊥PA,
而PA∩AC=A,
∴BC⊥平面PAC.
13.(2019年揭阳学考模拟)如图,在三棱锥P -ABC中,平面PAB⊥平面ABC,△PAB是等边三角形,AC⊥BC,且AC=BC=2,O,D分别是AB,PB的中点.
(1)求证:PA∥平面COD;
(2)求三棱锥P ABC的体积.
(1)证明:∵O,D分别是AB,PB的中点,
∴OD∥AP.
又PA平面COD,OD 平面COD,
∴PA∥平面COD.
(2)连接OP,
由△PAB是等边三角形,则OP⊥AB
又∵平面PAB⊥平面ABC,
∴OP⊥面ABC,且OP=×2=.
∴三棱锥P ABC的体积V=S△ABC×OP=××22×=.
14.(2018年广东省普通高中数学学业水平考试模拟题)已知四棱锥P -ABCD中,PD⊥平面ABCD,四边形ABCD是正方形,E是PA的中点.
求证:(1)PC∥平面EBD;
(2)平面PBC⊥平面PCD.
(1)连接AC交BD于O,连接EO,
∵E,O分别为PA,AC的中点,
∴EO∥PC.
∵PC平面EBD,EO 平面EBD,
∴PC∥平面EBD.
(2)∵PD⊥平面ABCD,BC 平面ABCD,
∴PD⊥BC,
∵ABCD为正方形,
∴BC⊥CD,
又∵PD∩CD=D,
∴BC⊥平面PCD,
∵BC 平面PBC,
∴平面PBC⊥平面PCD.
15.(2020年广东学考模拟)在四棱锥S -ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2,BA=BS=4.
(1)证明:BD⊥平面SAD;
(2)求点C到平面SAB的距离.
(1)证明:△ADB中,由余弦定理可得BD=2,
∴BD2+AD2=AB2,
∴AD⊥BD.
取SA的中点E,连接DE,BE,则DE⊥SA,BE⊥SA,
∵DE∩BE=E,
∴SA⊥平面BDE,
∴SA⊥BD,
∵SA∩AD=A,
∴BD⊥平面SAD;
(2)点C到平面SAB的距离=点D到平面SAB的距离h.
△SAD中,∠SAD=30°,AD=SD=2,
∴S△SAD=×2×2×=3,
△SAB中,BA=BS=4,SA=6,
∴S△SAB=×6×=3,
由等体积可得×3×2=×3h,
∴h=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第七章 立体几何
1.圆柱、圆锥、圆台的侧面展开图及侧面积公式
圆柱 圆锥 圆台
侧面展开图
侧面积公式 S圆柱侧=2πrl S圆锥侧=πrl S圆台侧=π(r+r′)l
2.空间几何体的表面积与体积公式
名称几何体 表面积 体积
柱体(棱柱和圆柱) S表面积=S侧+2S底 V=Sh
锥体(棱锥和圆锥) S表面积=S侧+S底 V=Sh
球 S=4πr2 V=πr3
3.直线与平面平行的判定定理和性质定理
文字语言 图形语言 符号语言
判定定理 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行(线线平行 线面平行) ∵l∥a,a α,lα,∴l∥α
性质定理 一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行 线线平行”) ∵l∥α,l β,α∩β=b,∴l∥b
4.平面与平面平行的判定定理和性质定理
文字语言 图形语言 符号语言
判定定理 一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为“线面平行 面面平行”) ∵a∥β,b∥β,a∩b=P,a α,b α,∴α∥β
性质定理 如果两个平行平面同时和第三个平面相交,那么它们的交线平行 ∵α∥β,α∩γ=a,β∩γ=b,∴a∥b
5.与垂直相关的平行的判定
(1)a⊥α,b⊥α a∥b.
(2)a⊥α,a⊥β α∥β.
6.平行问题的转化关系
7.直线与平面垂直
(1)直线和平面垂直的定义: 直线l与平面α内的任意一条直线都垂直,就说直线l与平面α互相垂直.
(2)直线与平面垂直的判定定理及性质定理:
文字语言 图形语言 符号语言
判定定理 一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直 l⊥α
性质定理 垂直于同一个平面的两条直线平行 a∥b
8.直线和平面所成的角
平面的一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角.
范围:.
9.平面与平面垂直的判定定理与性质定理
文字语言 图形语言 符号语言
判定定理 一个平面过另一个平面的垂线,则这两个平面垂直 α⊥β
性质定理 两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直 l⊥α
直线与平面垂直的五个结论
(1)若一条直线垂直于一个平面,则这条直线垂直于这个平面内的任意直线.
(2)若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.
(3)垂直于同一条直线的两个平面平行.
(4)一条直线垂直于两平行平面中的一个,则这条直线与另一个平面也垂直.
(5)两个相交平面同时垂直于第三个平面,它们的交线也垂直于第三个平面.
[学业水平考试真题]
1.(2017年1月广东学考)如图,在四棱锥P-ABCD中,PA⊥AB,PA⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC=2,E为PC的中点.
(1) 证明:AP⊥CD;
(2) 求三棱锥P-ABC的体积;
(3) 证明:AE⊥平面PCD.
2.(2018年1月广东学考)如图所示,一个空间几何体的正视图和侧视图都是矩形,俯视图是正方形,则该几何体的体积为( )
A.1 B.2 C.4 D.8
3.(2018年1月广东学考)如图所示,在三棱锥P -ABC中,PA⊥平面ABC,PB=BC,F为BC的中点,DE垂直平分PC,且DE分别交AC,PC于点D,E.
(1)证明:EF∥平面ABP;
(2)证明:BD⊥AC.
4.(2019年1月广东学考)如图,长方体ABCD -A1B1C1D1中,AB=AD=1,BD1=2,则AA1=( )
A.1 B. C.2 D.
5.(2019年1月广东学考)如图,三棱锥P -ABC中,PA⊥PB,PB⊥PC,PC⊥PA,PA=PB=PC=2,E是AC的中点,点F在线段PC上.
(1)证明:PB⊥AC;
(2)若PA∥平面BEF,求四棱锥B -APFE的体积.
(参考公式:锥体的体积公式为V=Sh,其中S是底面积,h是高.)
6.(2020年1月广东学考)一个棱长为2的正方体,其顶点均在同一球的球面上,则该球的表面积是( )
(参考公式:球的表面积公式为S=4πR2,其中R是球的半径)
A.3π B.4π C.8π D.12π
7.(2020年1月广东学考)如图,直三棱柱ABC -A1B1C1中,底面是边长为2的等边三角形,点D,E分别是BC,AB1的中点.
(1)证明:DE∥平面ACC1A1;
(2)若BB1=1,证明:C1D⊥平面ADE.
8.(2021年1月广东学考)已知直线,若//,,则下列结论正确的是( )
A.// B.与是异面直线 C. D.以上均有可能
9.(2021年1月广东学考)如图3,在四棱锥中,底面ABCD是边长为2的菱形,PA=AC=2,,E,F分别为PD,BC的中点.
(1)求三棱锥的体积;
(2)证明:.
[学业水平考试最新模拟题]
1.(2019年蛇口学考模拟)如图是一个几何体的三视图,则该几何体为( )
A.球 B.圆柱 C.圆台 D.圆锥
第1题图 第2题图
2.(2018年广东省普通高中学业水平测试数学模拟测试卷(考前压题篇))若如图是一个几何体的三视图,则这个几何体是( )
A.圆锥 B.棱柱 C.圆柱 D.棱锥
3.(2019年韶关市学考模拟)某几何体的三视图如图所示,则该几何体的体积为( )
A.π B.48π C.π D.64π
4.(2020年广东学考模拟)某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )
A.8cm3 B.12cm3 C.cm3 D.cm3
5.(2019年深圳高一期末)α,β,γ为三个不重合的平面,a,b,c为三条不同的直线,则下列命题中不正确的是( )
① a∥b; ② a∥b; ③ α∥β;
④ α∥β; ⑤ α∥a; ⑥ a∥α.
A.④⑥ B.②③⑥ C.②③⑤⑥ D.②③
6.(2018年广东省普通高中数学学业水平考试模拟题)已知互相垂直的平面α,β交于直线l.若直线m,n满足m∥α,n⊥β,则( )
A.m∥l B.m∥n C.n⊥l D.m⊥n
7.(2015年浙江高考)设α,β是两个不同的平面,l,m是两条不同的直线,且l α,m β.( )
A.若l⊥β,则α⊥β B.若α⊥β,则l⊥m
C.若l∥β,则α∥β D.若α∥β,则l∥m
8.(2021年全国Ⅰ)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为( )
A. B. C. D.
9.(2016年全国Ⅱ)体积为8的正方体的顶点都在同一球面上,则该球的表面积为( )
A.12π B.π C.8π D.4π
10.已知一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为________.
11.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是AB,AD的中点,则异面直线B1C与EF所成角的大小为( )
A.30° B.45° C.60° D.90°
12.如图,已知四棱锥P -ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD.
(1)求证:AB∥平面PDC;
(2)求证:BC⊥平面PAC.
13.(2019年揭阳学考模拟)如图,在三棱锥P -ABC中,平面PAB⊥平面ABC,△PAB是等边三角形,AC⊥BC,且AC=BC=2,O,D分别是AB,PB的中点.
(1)求证:PA∥平面COD;
(2)求三棱锥P ABC的体积.
14.(2018年广东省普通高中数学学业水平考试模拟题)已知四棱锥P -ABCD中,PD⊥平面ABCD,四边形ABCD是正方形,E是PA的中点.
求证:(1)PC∥平面EBD;
(2)平面PBC⊥平面PCD.
15.(2020年广东学考模拟)在四棱锥S -ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2,BA=BS=4.
(1)证明:BD⊥平面SAD;
(2)求点C到平面SAB的距离.
参考答案
[学业水平考试真题]
1.(2017年1月广东学考)如图,在四棱锥P-ABCD中,PA⊥AB,PA⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC=2,E为PC的中点.
(1) 证明:AP⊥CD;
(2) 求三棱锥P-ABC的体积;
(3) 证明:AE⊥平面PCD.
(1)证明:因为PA⊥AB,PA⊥AD,AB 平面ABCD,AD 平面ABCD,AB∩AD=A,
所以PA⊥平面ABCD,
又CD 平面ABCD,
所以AP⊥CD.
(2)解:由(1)可知AP⊥平面ABC,
所以VP-ABC=S△ABC·AP,
又S△ABC=AB·BC·sin ∠ABC=×2×2×sin 60°=,
所以VP-ABC=××2=.
(3)证明:因为CD⊥AP,CD⊥AC,AP 平面APC,AC 平面APC,AP∩AC=A,
所以CD⊥平面APC,
又AE 平面APC,
所以CD⊥AE,
由AB=BC=2且∠ABC=60°得△ABC为等边三角形,且AC=2,
又因为AP=2,且E为PC的中点,
所以AE⊥PC,
又AE⊥CD,PC 平面PCD,CD 平面PCD,PC∩CD=C,
所以AE⊥平面PCD.
2.(2018年1月广东学考)如图所示,一个空间几何体的正视图和侧视图都是矩形,俯视图是正方形,则该几何体的体积为( C )
A.1 B.2 C.4 D.8
3.(2018年1月广东学考)如图所示,在三棱锥P -ABC中,PA⊥平面ABC,PB=BC,F为BC的中点,DE垂直平分PC,且DE分别交AC,PC于点D,E.
(1)证明:EF∥平面ABP;
(2)证明:BD⊥AC.
证明: (1)∵DE垂直平分PC,
∴E为PC的中点,
又∵F为BC的中点,
∴EF为△BCP的中位线,
∴EF∥BP,
又∵EF平面ABP,BP 平面ABP,
∴EF∥平面ABP.
(2)连接BE,
∵PB=BC,E为PC的中点,
∴PC⊥BE,
∵DE垂直平分PC,
∴PC⊥DE,
又∵BE∩DE=E,BE 平面BDE,DE 平面BDE,
∴PC⊥平面BDE,
又∵BD 平面BDE,
∴PC⊥BD,
∵PA⊥平面ABC,BD 平面ABC,
∴PA⊥BD,
又∵PC∩PA=P,PC 平面PAC,PA 平面PAC,
∴BD⊥平面PAC,
又∵AC 平面PAC,
∴BD⊥AC.
4.(2019年1月广东学考)如图,长方体ABCD -A1B1C1D1中,AB=AD=1,BD1=2,则AA1=( B )
A.1 B. C.2 D.
5.(2019年1月广东学考)如图,三棱锥P -ABC中,PA⊥PB,PB⊥PC,PC⊥PA,PA=PB=PC=2,E是AC的中点,点F在线段PC上.
(1)证明:PB⊥AC;
(2)若PA∥平面BEF,求四棱锥B -APFE的体积.
(参考公式:锥体的体积公式为V=Sh,其中S是底面积,h是高.)
(1)∵PA⊥PB,PB⊥PC,PC∩PA=P,
∴PB⊥平面PAC,
又AC 平面PAC,
∴PB⊥AC.
(2)∵PA∥平面BEF,PA 平面PAC,平面PAC∩平面BEF=EF,
∴EF∥PA,
∴四边形PAEF为梯形,
又∵PA⊥PC,
∴四边形PAEF为直角梯形,
又∵E是AC的中点,
∴F为PC的中点,
∴PF=PC=1,EF=PA=1,
∴直角梯形APFE的面积S=×PF=.
由(1)知PB⊥平面APFE.
∴四棱锥B APFE的体积V=S·PB=1.
6.(2020年1月广东学考)一个棱长为2的正方体,其顶点均在同一球的球面上,则该球的表面积是( D )
(参考公式:球的表面积公式为S=4πR2,其中R是球的半径)
A.3π B.4π C.8π D.12π
7.(2020年1月广东学考)如图,直三棱柱ABC -A1B1C1中,底面是边长为2的等边三角形,点D,E分别是BC,AB1的中点.
(1)证明:DE∥平面ACC1A1;
(2)若BB1=1,证明:C1D⊥平面ADE.
(1)证明:连接A1B,A1C,
在直三棱柱ABC-A1B1C1中,侧面ABB1A1是矩形,
因为点E是AB1的中点,
所以点E是A1B的中点,
又因为点D是BC的中点,
所以DE∥A1C,
因为DE平面ACC1A1,A1C 平面ACC1A1,
所以DE∥平面ACC1A1.
(2)连接B1D,在直三棱柱ABC A1B1C1中,
因为BB1⊥平面ABC,AD 平面ABC,
所以BB1⊥AD,
又因为底面ABC是等边三角形,D为BC的中点,
所以BC⊥AD,
又BC∩BB1=B,
所以AD⊥平面B1BCC1,
又C1D 平面B1BCC1,
所以AD⊥C1D,
由BC=2,得BD=1,又BB1=CC1=1,
所以DB1=C1D=,
所以DB+C1D2=B1C,
所以C1D⊥DB1,DB1∩AD=D,
所以C1D⊥平面ADB1,
即C1D⊥平面ADE.
8.(2021年1月广东学考)已知直线,若//,,则下列结论正确的是( D )
A.// B.与是异面直线 C. D.以上均有可能
9.(2021年1月广东学考)如图3,在四棱锥中,底面ABCD是边长为2的菱形,PA=AC=2,,E,F分别为PD,BC的中点.
(1)求三棱锥的体积;
(2)证明:.
(1)设AC与BD的交点为O, 因为底面ABCD是边长为2的菱形,
所以,因为AC=2,所以OA=OC==1,
在,故BD=2OB=2,
所以,
因为,所以为三棱锥的高h,
所以三棱锥的体积.
(2)取PA的中点G,
因为E为PD的中点,
所以,
又因为F为BC的中点,四边形ABCD为菱形,
所以,
所以,
故四边形BFEG为平行四边形,
所以BG//EF,
因为,
所以.
[学业水平考试最新模拟题]
1.(2019年蛇口学考模拟)如图是一个几何体的三视图,则该几何体为( D )
A.球 B.圆柱 C.圆台 D.圆锥
第1题图 第2题图
2.(2018年广东省普通高中学业水平测试数学模拟测试卷(考前压题篇))若如图是一个几何体的三视图,则这个几何体是( C )
A.圆锥 B.棱柱 C.圆柱 D.棱锥
3.(2019年韶关市学考模拟)某几何体的三视图如图所示,则该几何体的体积为( A )
A.π B.48π C.π D.64π
4.(2020年广东学考模拟)某几何体的三视图如图所示(单位:cm),则该几何体的体积是( C )
A.8cm3 B.12cm3 C.cm3 D.cm3
5.(2019年深圳高一期末)α,β,γ为三个不重合的平面,a,b,c为三条不同的直线,则下列命题中不正确的是( C )
① a∥b; ② a∥b; ③ α∥β;
④ α∥β; ⑤ α∥a; ⑥ a∥α.
A.④⑥ B.②③⑥ C.②③⑤⑥ D.②③
6.(2018年广东省普通高中数学学业水平考试模拟题)已知互相垂直的平面α,β交于直线l.若直线m,n满足m∥α,n⊥β,则( C )
A.m∥l B.m∥n C.n⊥l D.m⊥n
7.(2015年浙江高考)设α,β是两个不同的平面,l,m是两条不同的直线,且l α,m β.( A )
A.若l⊥β,则α⊥β B.若α⊥β,则l⊥m
C.若l∥β,则α∥β D.若α∥β,则l∥m
8.(2021年全国Ⅰ)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为( B )
A. B. C. D.
9.(2016年全国Ⅱ)体积为8的正方体的顶点都在同一球面上,则该球的表面积为( A )
A.12π B.π C.8π D.4π
10.已知一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为________.
11.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是AB,AD的中点,则异面直线B1C与EF所成角的大小为( C )
A.30° B.45° C.60° D.90°
12.如图,已知四棱锥P -ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD.
(1)求证:AB∥平面PDC;
(2)求证:BC⊥平面PAC.
(1)∵AB∥CD,CD 平面PDC,AB 平面PDC,
∴AB∥平面PDC.
(2)在直角梯形ABCD中,过点C作CE⊥AB于点E,则四边形ADCE为矩形,
∴AE=DC=1,又AB=2,
∴BE=1,
在Rt△BEC中,∠ABC=45°,
∴CE=BE=1,CB=,
在Rt△ACE中,AC==,
∴AC2+BC2=AB2,
∴BC⊥AC,
又PA⊥平面ABCD,BC 平面ABCD,
∴BC⊥PA,
而PA∩AC=A,
∴BC⊥平面PAC.
13.(2019年揭阳学考模拟)如图,在三棱锥P -ABC中,平面PAB⊥平面ABC,△PAB是等边三角形,AC⊥BC,且AC=BC=2,O,D分别是AB,PB的中点.
(1)求证:PA∥平面COD;
(2)求三棱锥P ABC的体积.
(1)证明:∵O,D分别是AB,PB的中点,
∴OD∥AP.
又PA平面COD,OD 平面COD,
∴PA∥平面COD.
(2)连接OP,
由△PAB是等边三角形,则OP⊥AB
又∵平面PAB⊥平面ABC,
∴OP⊥面ABC,且OP=×2=.
∴三棱锥P ABC的体积V=S△ABC×OP=××22×=.
14.(2018年广东省普通高中数学学业水平考试模拟题)已知四棱锥P -ABCD中,PD⊥平面ABCD,四边形ABCD是正方形,E是PA的中点.
求证:(1)PC∥平面EBD;
(2)平面PBC⊥平面PCD.
(1)连接AC交BD于O,连接EO,
∵E,O分别为PA,AC的中点,
∴EO∥PC.
∵PC平面EBD,EO 平面EBD,
∴PC∥平面EBD.
(2)∵PD⊥平面ABCD,BC 平面ABCD,
∴PD⊥BC,
∵ABCD为正方形,
∴BC⊥CD,
又∵PD∩CD=D,
∴BC⊥平面PCD,
∵BC 平面PBC,
∴平面PBC⊥平面PCD.
15.(2020年广东学考模拟)在四棱锥S -ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2,BA=BS=4.
(1)证明:BD⊥平面SAD;
(2)求点C到平面SAB的距离.
(1)证明:△ADB中,由余弦定理可得BD=2,
∴BD2+AD2=AB2,
∴AD⊥BD.
取SA的中点E,连接DE,BE,则DE⊥SA,BE⊥SA,
∵DE∩BE=E,
∴SA⊥平面BDE,
∴SA⊥BD,
∵SA∩AD=A,
∴BD⊥平面SAD;
(2)点C到平面SAB的距离=点D到平面SAB的距离h.
△SAD中,∠SAD=30°,AD=SD=2,
∴S△SAD=×2×2×=3,
△SAB中,BA=BS=4,SA=6,
∴S△SAB=×6×=3,
由等体积可得×3×2=×3h,
∴h=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
