北师大版(2019)高中数学必修2《6.5垂直关系》第2课时课件(共17张PPT)
文档属性
| 名称 | 北师大版(2019)高中数学必修2《6.5垂直关系》第2课时课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 298.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-08 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
6.5 垂直关系
第2课时
导入新课
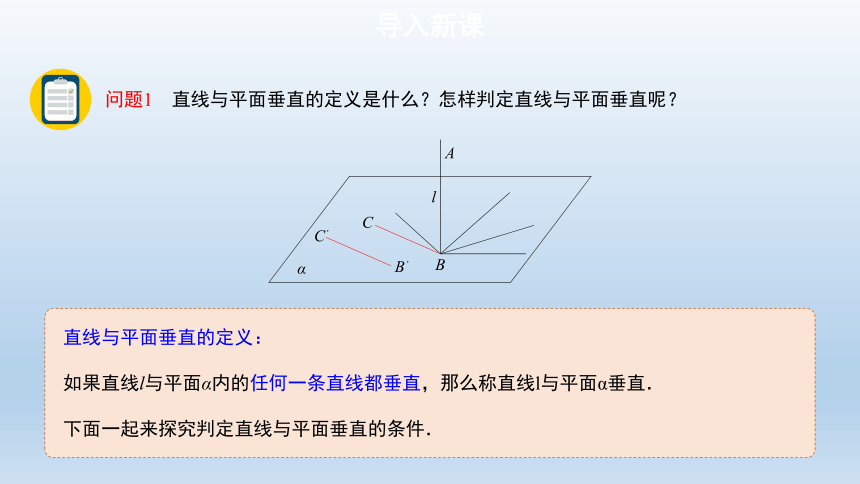
问题1 直线与平面垂直的定义是什么?怎样判定直线与平面垂直呢?
直线与平面垂直的定义:
下面一起来探究判定直线与平面垂直的条件.
如果直线l与平面α内的任何一条直线都垂直,那么称直线l与平面α垂直.
A
B
C
B’
C’
l
α
新知探究
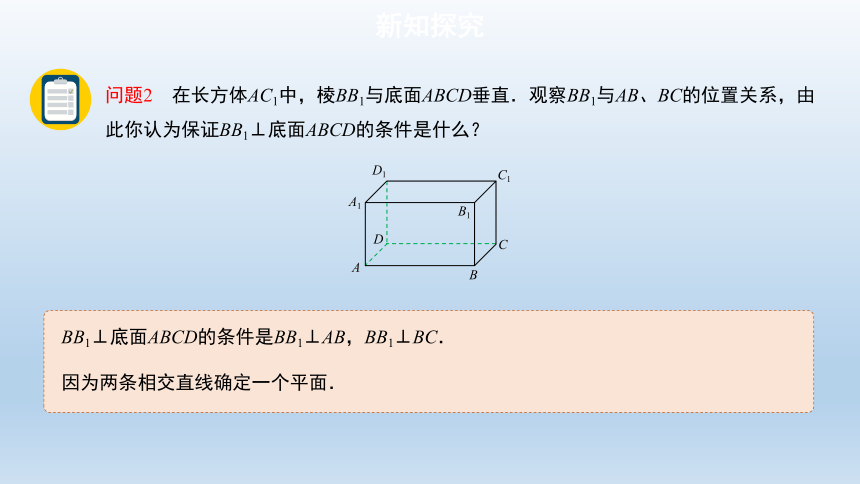
BB1⊥底面ABCD的条件是BB1⊥AB,BB1⊥BC.
因为两条相交直线确定一个平面.
问题2 在长方体AC1中,棱BB1与底面ABCD垂直.观察BB1与AB、BC的位置关系,由此你认为保证BB1⊥底面ABCD的条件是什么?
A
B
C
D
C1
D1
B1
A1
导入新课
如果一条直线和一个平面内的两条相交直线都垂直,那么该直线与平面垂直.
追问 由问题3,你能猜想出判断一条直线与一个平面垂直的方法吗?
当折痕AD是BC边上的高的时,AD所在直线与桌面所在平面垂直.
A
B
C
D
问题3 过 ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放在桌面上
(BD、DC与桌面接触).
(2)如何翻折才能使折痕AD与桌面所在平面垂直?
(1)折痕AD与桌面垂直吗?
A
B
C
D
新知探究
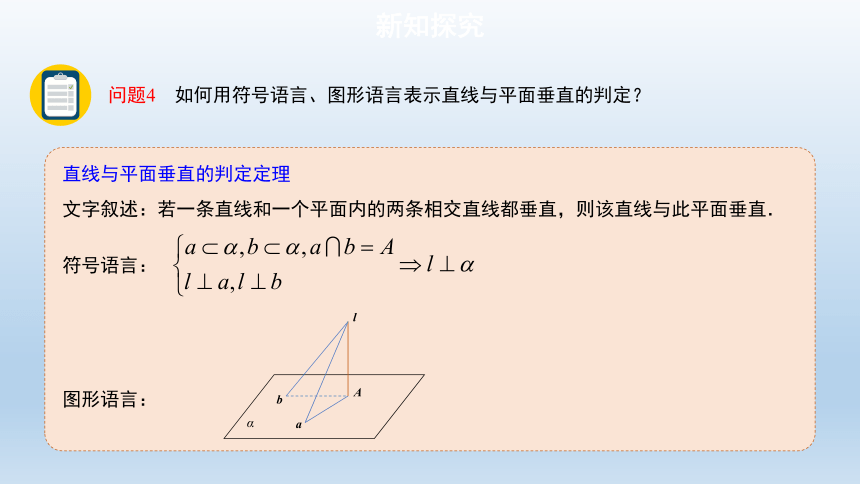
问题4 如何用符号语言、图形语言表示直线与平面垂直的判定?
图形语言:
α
l
b
a
A
符号语言:
文字叙述:若一条直线和一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
直线与平面垂直的判定定理
新知探究
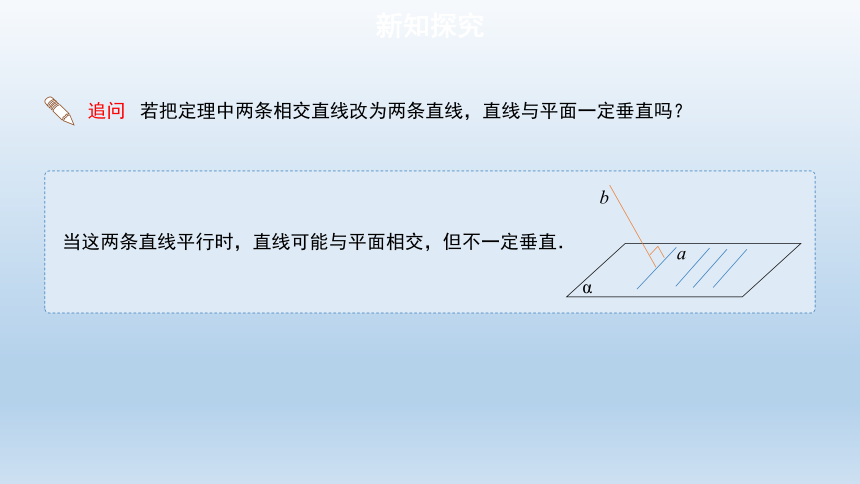
追问 若把定理中两条相交直线改为两条直线,直线与平面一定垂直吗?
当这两条直线平行时,直线可能与平面相交,但不一定垂直.
b
α
a
初步应用
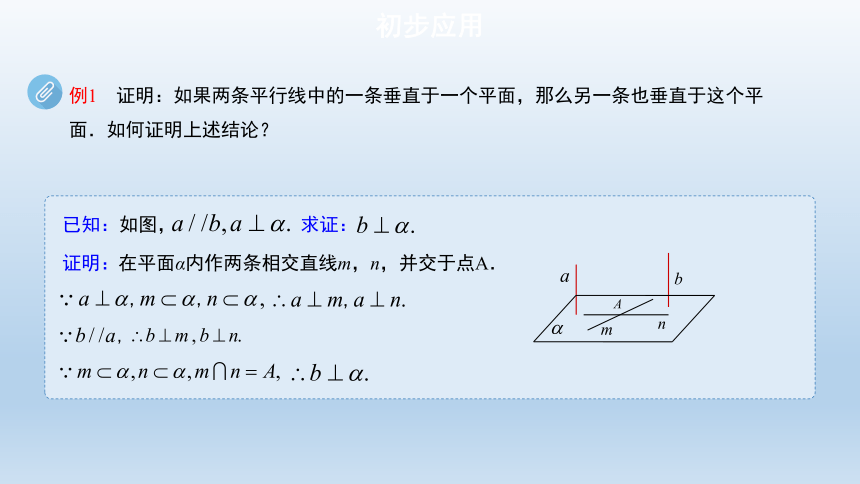
例1 证明:如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于这个平面.如何证明上述结论?
A
已知:如图,
求证:
证明:
在平面α内作两条相交直线m,n,并交于点A.
初步应用
例2 如图所示,长杆l与地面α相交于点O,在杆子上距地面2m的点P处挂一根长2.5m的绳子,拉紧绳子并把它的下端放在地面上的点A,或点B(A,B,O三点不在同一条直线上).如果A,B两点和点O的距离都是1.5m,那么长杆l和地面是否垂直?为什么?
解析:长杆l和地面垂直.
课堂练习
若直线a⊥直线b,直线b⊥平面α,则直线a与平面α的位置关系是( )
1
D
A.a⊥平面α
C.a 平面α
B.a //平面α
D.a 平面α或a //平面α
b
a
α
b
a
α
故选:D.
解析:
如图1所示,直线a 平面α.
如图2所示,直线a //平面α.
课堂练习
2
如图所示,在底面是菱形的四棱锥P-ABCD中,∠ABC=,PA=AC=a, PB=PD=,
求证:PA⊥面ABCD.
P
B
C
D
A
∴PA⊥面ABCD
解析:
∵底面ABCD是菱形,∠ABC=
∴AB=AD=AC=a
在△PAB中,由于
∴PA⊥AB,
同理PA⊥AD
归纳小结
(1)直线与平面垂直的判定定理中要注意什么?
(2)用线面垂直的判定定理证明线面垂直的步骤是什么?
问题5 本节课我们学习了直线与平面垂直的判定定理及其应用,请你通过下列问题,
归纳所学知识.
(1)直线与平面垂直的判定定理中要注意必须是平面内两相交直线.
(2)利用线面垂直的判定定理证明线面垂直的步骤:
①在这个平面内找两条直线,使它们和这条直线垂直;
②确定这个平面内的两条直线是相交的直线;
③根据判定定理得出结论.
作业布置
作业:教科书第235页,A组第4,5,6,10题,第203页B组第1题.
1
目标检测
C
如果一条直线垂直于一个平面内的两条直线有如下情况:
①三角形的两条边; ②梯形的两条边; ③圆的两条直径; ④正六边形的两条边.
不能保证直线与平面垂直的是( )
A.①③
C.②④
B.②
D.①②④
解析: ①三角形任意两边为相交直线.
③直径必相交.
故选:C.
②若与两底所在直线垂直,则不能判断线面垂直.
④若垂直于正六边形互相平行的边,则不能保证线面垂直.
2
目标检测
B
在正方体ABCD-A1B1C1D1中,与AD1垂直的平面是( )
A.平面DD1C1C
B.平面A1DB1
C.平面A1B1C1D1
D.平面A1DB
解析:∵AD1⊥A1D,AD1⊥A1B1,又A1D∩A1B1=A1,
∴AD1⊥平面A1DB1.
故选:B.
3
目标检测
D
已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABCDEF,则下列结论不正确的是( )
A.CD∥平面PAF
B.DF⊥平面PAF
C.CF∥平面PAB
D.CF⊥平面PAD
解析:由正六边形的性质及PA⊥平面ABCDEF,
因为四边形ACDF不是正方形,CF与AD不垂直.
故选:D.
可推得A,B,C均正确,而D不正确.
4
目标检测
如图,Rt△ABC所在平面外有一点S,且SA=SB=SC,点D为斜边AC的中点.
(1)求证:SD⊥平面ABC;
(2)若AB=BC,求证:BD⊥平面SAC.
证明:(1)∵SA=SC,D为AC中点,
又∵SA=SB,SD=SD,
∴△ADS≌△BDS,
又AC∩BD=D,AC,BD 平面ABC,
∴SD⊥AC,Rt△ABC中,AD=CD=BD.
∴SD⊥BD.
∴SD⊥平面ABC.
4
目标检测
如图,Rt△ABC所在平面外有一点S,且SA=SB=SC,点D为斜边AC的中点.
(1)求证:SD⊥平面ABC;
(2)若AB=BC,求证:BD⊥平面SAC.
证明:(2)∵BA=BC,D为AC中点,
由(1)知SD⊥面ABC,又BD 平面ABC,
于是BD垂直于平面SAC内的两条相交直线,
∴BD⊥平面SAC.
∴BD⊥AC.
∴SD⊥BD,
6.5 垂直关系
第2课时
导入新课
问题1 直线与平面垂直的定义是什么?怎样判定直线与平面垂直呢?
直线与平面垂直的定义:
下面一起来探究判定直线与平面垂直的条件.
如果直线l与平面α内的任何一条直线都垂直,那么称直线l与平面α垂直.
A
B
C
B’
C’
l
α
新知探究
BB1⊥底面ABCD的条件是BB1⊥AB,BB1⊥BC.
因为两条相交直线确定一个平面.
问题2 在长方体AC1中,棱BB1与底面ABCD垂直.观察BB1与AB、BC的位置关系,由此你认为保证BB1⊥底面ABCD的条件是什么?
A
B
C
D
C1
D1
B1
A1
导入新课
如果一条直线和一个平面内的两条相交直线都垂直,那么该直线与平面垂直.
追问 由问题3,你能猜想出判断一条直线与一个平面垂直的方法吗?
当折痕AD是BC边上的高的时,AD所在直线与桌面所在平面垂直.
A
B
C
D
问题3 过 ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放在桌面上
(BD、DC与桌面接触).
(2)如何翻折才能使折痕AD与桌面所在平面垂直?
(1)折痕AD与桌面垂直吗?
A
B
C
D
新知探究
问题4 如何用符号语言、图形语言表示直线与平面垂直的判定?
图形语言:
α
l
b
a
A
符号语言:
文字叙述:若一条直线和一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
直线与平面垂直的判定定理
新知探究
追问 若把定理中两条相交直线改为两条直线,直线与平面一定垂直吗?
当这两条直线平行时,直线可能与平面相交,但不一定垂直.
b
α
a
初步应用
例1 证明:如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于这个平面.如何证明上述结论?
A
已知:如图,
求证:
证明:
在平面α内作两条相交直线m,n,并交于点A.
初步应用
例2 如图所示,长杆l与地面α相交于点O,在杆子上距地面2m的点P处挂一根长2.5m的绳子,拉紧绳子并把它的下端放在地面上的点A,或点B(A,B,O三点不在同一条直线上).如果A,B两点和点O的距离都是1.5m,那么长杆l和地面是否垂直?为什么?
解析:长杆l和地面垂直.
课堂练习
若直线a⊥直线b,直线b⊥平面α,则直线a与平面α的位置关系是( )
1
D
A.a⊥平面α
C.a 平面α
B.a //平面α
D.a 平面α或a //平面α
b
a
α
b
a
α
故选:D.
解析:
如图1所示,直线a 平面α.
如图2所示,直线a //平面α.
课堂练习
2
如图所示,在底面是菱形的四棱锥P-ABCD中,∠ABC=,PA=AC=a, PB=PD=,
求证:PA⊥面ABCD.
P
B
C
D
A
∴PA⊥面ABCD
解析:
∵底面ABCD是菱形,∠ABC=
∴AB=AD=AC=a
在△PAB中,由于
∴PA⊥AB,
同理PA⊥AD
归纳小结
(1)直线与平面垂直的判定定理中要注意什么?
(2)用线面垂直的判定定理证明线面垂直的步骤是什么?
问题5 本节课我们学习了直线与平面垂直的判定定理及其应用,请你通过下列问题,
归纳所学知识.
(1)直线与平面垂直的判定定理中要注意必须是平面内两相交直线.
(2)利用线面垂直的判定定理证明线面垂直的步骤:
①在这个平面内找两条直线,使它们和这条直线垂直;
②确定这个平面内的两条直线是相交的直线;
③根据判定定理得出结论.
作业布置
作业:教科书第235页,A组第4,5,6,10题,第203页B组第1题.
1
目标检测
C
如果一条直线垂直于一个平面内的两条直线有如下情况:
①三角形的两条边; ②梯形的两条边; ③圆的两条直径; ④正六边形的两条边.
不能保证直线与平面垂直的是( )
A.①③
C.②④
B.②
D.①②④
解析: ①三角形任意两边为相交直线.
③直径必相交.
故选:C.
②若与两底所在直线垂直,则不能判断线面垂直.
④若垂直于正六边形互相平行的边,则不能保证线面垂直.
2
目标检测
B
在正方体ABCD-A1B1C1D1中,与AD1垂直的平面是( )
A.平面DD1C1C
B.平面A1DB1
C.平面A1B1C1D1
D.平面A1DB
解析:∵AD1⊥A1D,AD1⊥A1B1,又A1D∩A1B1=A1,
∴AD1⊥平面A1DB1.
故选:B.
3
目标检测
D
已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABCDEF,则下列结论不正确的是( )
A.CD∥平面PAF
B.DF⊥平面PAF
C.CF∥平面PAB
D.CF⊥平面PAD
解析:由正六边形的性质及PA⊥平面ABCDEF,
因为四边形ACDF不是正方形,CF与AD不垂直.
故选:D.
可推得A,B,C均正确,而D不正确.
4
目标检测
如图,Rt△ABC所在平面外有一点S,且SA=SB=SC,点D为斜边AC的中点.
(1)求证:SD⊥平面ABC;
(2)若AB=BC,求证:BD⊥平面SAC.
证明:(1)∵SA=SC,D为AC中点,
又∵SA=SB,SD=SD,
∴△ADS≌△BDS,
又AC∩BD=D,AC,BD 平面ABC,
∴SD⊥AC,Rt△ABC中,AD=CD=BD.
∴SD⊥BD.
∴SD⊥平面ABC.
4
目标检测
如图,Rt△ABC所在平面外有一点S,且SA=SB=SC,点D为斜边AC的中点.
(1)求证:SD⊥平面ABC;
(2)若AB=BC,求证:BD⊥平面SAC.
证明:(2)∵BA=BC,D为AC中点,
由(1)知SD⊥面ABC,又BD 平面ABC,
于是BD垂直于平面SAC内的两条相交直线,
∴BD⊥平面SAC.
∴BD⊥AC.
∴SD⊥BD,
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
